

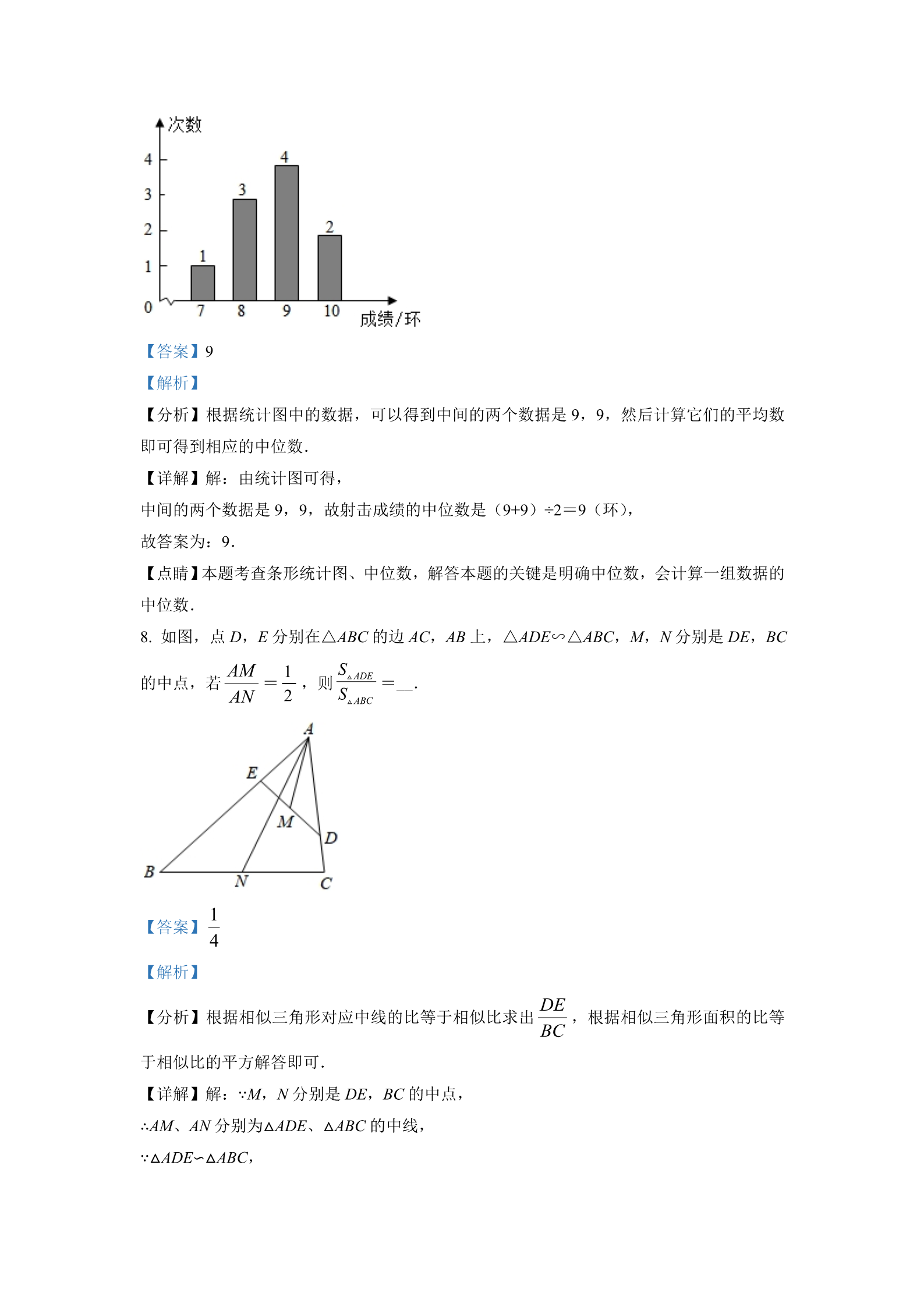


2021 年江苏省镇江市中考数学试卷 一、填空题(本大题共 12 小题) 5 1. 的绝对值是__________. 【答案】5 【解析】 【分析】根据绝对值的定义计算即可. 【详解】解:|-5|=5, 故答案为:5. 【点睛】本题考查了绝对值的定义,掌握知识点是解题关键. 的有意义 x 的取值范围是__. 2. 使 x 7 【答案】x≥7 【解析】 【分析】直接利用二次根式被开方数是非负数,进而得出答案. 【详解】解: 有意义,则 x﹣7≥0, x 7 解得:x≥7. 故答案为:x≥7. 【点睛】]此题主要考查了二次根式有意义的条件,正确掌握二次根式被开方数是非负数是 解题关键. 3. 8 的立方根是___. 【答案】2 【解析】 的【分析】利用立方根 定义计算即可得到结果. 【详解】解:8 的立方根为 2, 故答案为:2. 【点睛】此题主要考查立方根的求解,解题的关键是熟知立方根的定义. 4. 如图,花瓣图案中的正六边形 ABCDEF 的每个内角的度数是__. 【答案】120° 【解析】 【分析】多边形的内角和可以表示成(n﹣2)•180°,因为所给多边形的每个内角均相等,可设 这个正六边形的每一个内角的度数为 x,故又可表示成 6x,列方程可求解. 【详解】解:设这个正六边形的每一个内角的度数为 x, 则 6x=(6﹣2)•180°, 解得 x=120°. 故答案为:120°. 【点睛】本题考查根据多边形的内角和计算公式及求正多边形的内角的度数,解答时要会根 据公式进行正确运算、变形和数据处理. x(x 1) 0 5. 一元二次方程 的解是__________. x 0, x 1 【答案】 【解析】 12【分析】根据 x(x-1)=0 得到两个一元一次方程 x=0,x-1=0,求出方程的解即可. 【详解】x(x−1)=0, x=0 或 x+1=0, x1 0, x2 1 故答案为 x=0 或 x=-1. 【点睛】此题考查解一元二次方程、解一元一次方程,解题关键在于运用因式分解法. 6. 小丽的笔试成绩为 100 分,面试成绩为 90 分,若笔试成绩、面试成绩按 6:4 计算平均 成绩,则小丽的平均成绩是__分. 【答案】96 【解析】 【分析】根据加权平均数的公式计算可得. 1006 904 【详解】解:小丽的平均成绩是 =96(分), 6 4 故答案为:96. 【点睛】本题考查的是加权平均数的求法.本题易出现的错误是求 100,90这两个数的平均 数,对平均数的理解不正确. 7. 某射手在一次训练中共射出了 10 发子弹,射击成绩如图所示,则射击成绩的中位数是__ 环. 【答案】9 【解析】 【分析】根据统计图中的数据,可以得到中间的两个数据是 9,9,然后计算它们的平均数 即可得到相应的中位数. 【详解】解:由统计图可得, 中间的两个数据是 9,9,故射击成绩的中位数是(9+9)÷2=9(环), 故答案为:9. 【点睛】本题考查条形统计图、中位数,解答本题的关键是明确中位数,会计算一组数据的 中位数. 8. 如图,点 D,E 分别在△ABC 的边 AC,AB 上,△ADE∽△ABC,M,N 分别是 DE,BC SADE SABC AM AN 12的中点,若 =,则 =__. 1【答案】 4【解析】 DE BC 【分析】根据相似三角形对应中线的比等于相似比求出 ,根据相似三角形面积的比等 于相似比的平方解答即可. 【详解】解:∵M,N 分别是 DE,BC 的中点, ∴AM、AN 分别为△ADE、△ABC 的中线, ∵△ADE∽△ABC, DE BC AM AN 12∴∴==,SADE SABC DE 1=( )2= ,BC 41故答案为: .4【点睛】本题考查了相似三角形的性质,掌握相似三角形面积的比等于相似比的平方、相似 三角形对应中线的比等于相似比是解题的关键. 9. 如图,点 A,B,C,O 在网格中小正方形的顶点处,直线 l 经过点 C,O,将 ABC 沿 l 平移得到 MNO,M 是 A 的对应点,再将这两个三角形沿 l 翻折,P,Q 分别是 A,M 的对 应点.已知网格中每个小正方形的边长都等于 1,则 PQ 的长为__. 【答案】 10 【解析】 【分析】连接 PQ,AM,根据 PQ=AM 即可解答. 【详解】解:连接 PQ,AM, 由图形变换可知:PQ=AM, 22由勾股定理得:AM= ,1 3 10 ∴PQ= .10 故答案为: .10 【点睛】本题主要考查了翻折的性质,勾股定理等知识,明确翻折前后对应线段相等是解题 的关键. 10. 已知一次函数的图象经过点(1,2),且函数值 y 随自变量 x 的增大而减小,写出符合条 件的一次函数表达式__.(答案不唯一,写出一个即可) 【答案】y=﹣x+3 【解析】 【分析】由函数值 y 随自变量 x 的增大而减小,利用一次函数的性质可得出 k<0,取 k= ﹣1,由一次函数的图象经过点(1,2),利用一次函数图象上点的坐标特征可得出 2= ﹣1+b,解之即可得出 b 值,进而可得出符合条件的一次函数表达式. 【详解】解:设一次函数表达式为 y=kx+b. ∵函数值 y 随自变量 x 的增大而减小, ∴k<0,取 k=﹣1. 又∵一次函数的图象经过点(1,2), ∴2=﹣1+b, ∴b=3, ∴一次函数表达式为 y=﹣x+3. 故答案为:y=﹣x+3. 【点睛】本题考查了一次函数的性质以及一次函数图象上点的坐标特征,牢记“k>0,y 随 x 的增大而增大;k<0,y 随 x 的增大而减小”是解题的关键. 11. 一只不透明的袋子中装有 1 个黄球,现放若干个红球,它们与黄球除颜色外都相同,搅 匀后从中任意摸出两个球,使得 P(摸出一红一黄)=P(摸出两红),则放入的红球个数为 __. 【答案】3 【解析】 【分析】分别假设放入的红球个数为 1、2 和 3,画树状图列出此时所有等可能结果,从中 找到摸出一红一黄和两个红球的结果数,从而验证红球的个数是否符合题意. 【详解】解:(1)假设袋中红球个数为 1, 此时袋中由 1 个黄球、1 个红球, 搅匀后从中任意摸出两个球,P(摸出一红一黄)=1,P(摸出两红)=0,不符合题意. (2)假设袋中的红球个数为 2, 列树状图如下: 由图可知,共有 6 种情况,其中两次摸到红球的情况有 2 种,摸出一红一黄的有 4 种结果, 4 2 =2613=∴P(摸出一红一黄)= ,P(摸出两红)= ,不符合题意, 6 3 (3)假设袋中的红球个数为 3, 画树状图如下: 由图可知,共有 12 种情况,其中两次摸到红球的情况有 6 种,摸出一红一黄的有 6 种结果, 612=∴P(摸出一红一黄)=P(摸出两红)= ,符合题意, 12 所以放入的红球个数为 3, 故答案为:3. 【点睛】本题考查了列表法和树状图法,用到的知识点为:概率=所求情况数与总情况数之 比. 112. 如图,等腰三角形 ABC 中,AB=AC,BC=6,cos∠ABC= ,点P 在边 AC 上运动 3(可与点 A,C 重合),将线段 BP 绕点 P 逆时针旋转 120°,得到线段 DP,连接 BD,则 BD 长的最大值为__. 【答案】9 3【解析】 【分析】由旋转知△BPD 是顶角为 120°的等腰三角形,可求得 BD= BP,当 BP 最大时, 3BD 取最大值,即点 P 与点 A 重合时,BP=BA 最大,求出 AB 的长即可解决问题. 【详解】解:∵将线段 BP 绕点 P 逆时针旋转 120°,得到线段 DP, ∴BP=PD, ∴△BPD 是等腰三角形, ∴∠PBD=30°, 过点 P 作 PH⊥BD 于点 H, ∴BH=DH, BH BP 3∵cos30°= =,23∴BH= ∴BD= BP, BP, 23∴当 BP 最大时,BD 取最大值,即点 P 与点 A 重合时,BP=BA 最大, 过点 A 作 AG⊥BC 于点 G, ∵AB=AC,AG⊥BC, 1∴BG= BC=3, 21∵cos∠ABC= ,3BG AB 13∴,∴AB=9, ∴BD 最大值为: BP=9 .33故答案为:9 .3【点睛】本题主要考查了等腰三角形的性质和判定,三角函数等知识,证明出 BD= BP 3是解题的关键. 二、选择题(本大题共 6 小题,在每小题给出的四个选项中,恰有一项是符合 题目要求的) 13. 如图所示,该几何体的俯视图是( )A. 正方形 【答案】C 【解析】 B. 长方形 C. 三角形 D. 圆 【分析】根据俯视图的定义,从上面看该几何体,所得到的图形进行判断即可. 【详解】解:从上面看该几何体,所看到的图形是三角形. 故选:C. 【点睛】本题考查简单几何体的三视图,理解视图的意义,掌握俯视图的概念是正确判断的 前提. 14. 2021 年 1﹣4 月份,全国规模以上工业企业利润总额超 25900 亿元,其中 25900 用科学 记数法表示为( A. 25.9×103 2.59×105 )B. 2.59×104 C. 0.259×105 D. 【答案】B 【解析】 【分析】科学记数法的表示形式为 a×10n 的形式,其中 1≤|a|<10,n 为整数.确定 n 的值时, 要看把原数变成 a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数 绝对值≥10 时,n 是正整数;当原数的绝对值<1 时,n 是负整数. 【详解】解:25900=2.59×104, 故选:B. 【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为 a×10n 的形式,其中 1≤|a|<10,n 为整数,表示时关键要定 a 的值以及 n 的值. 15. 如图,∠BAC=36°,点 O 在边 AB 上,⊙O 与边 AC 相切于点 D,交边 AB 于点 E,F, 连接 FD,则∠AFD 等于( )A. 27° B. 29° C. 35° D. 37° 【答案】A 【解析】 【分析】连接 OD,根据切线的性质得到∠ADO=90°,根据直角三角形的性质得到∠AOD= 90°﹣36°=54°,根据圆周角定理即可得到结论. 【详解】解:连接 OD, ∵⊙O 与边 AC 相切于点 D, ∴∠ADO=90°, ∵∠BAC=36°, ∴∠AOD=90°﹣36°=54°, 11AFD AOD 54 27 ∴,22故选:A. 【点睛】本题考查了切线的性质,圆周角定理,正确的作出辅助线构造直角三角形是解题的 关键. 16. 如图,输入数值 1921,按所示的程序运算(完成一个方框内的运算后,把结果输入下一 个方框继续进行运算),输出的结果为( )A. 1840 B. 1921 C. 1949 D. 2021 【答案】D 【解析】 【分析】把 1921 代入程序中计算,判断即可得到结果. 【详解】解:把 1921 代入得:(1921﹣1840+50)×(﹣1)=﹣131<1000, 把﹣131 代入得:(﹣131﹣1840+50)×(﹣1)=1921>1000, 则输出结果为 1921+100=2021. 故选:D. 【点睛】此题考查了有理数的混合运算,弄清程序中的运算过程是解本题的关键. 17. 设圆锥的底面圆半径为 r,圆锥的母线长为 l,满足 2r+l=6,这样的圆锥的侧面积( )949492A. 有最大值 πB. 有最小值 πC. 有最大值 πD. 有最小 9值π2【答案】C 【解析】 【分析】由 2r+l=6,得出 l=6﹣2r,代入圆锥的侧面积公式:S 侧=πrl,利用配方法整理得 39出,S 侧=﹣2π(r﹣ )2+ π,再根据二次函数的性质即可求解. 22【详解】解:∵2r+l=6, ∴l=6﹣2r, 39∴圆锥的侧面积 S 侧=πrl=πr(6﹣2r)=﹣2π(r2﹣3r)=﹣2π[(r﹣ )2﹣ ]= 2439﹣2π(r﹣ )2+ π, 22392∴当 r= 时,S 侧有最大值 .2故选:C. 【点睛】本题考查了圆锥的计算,二次函数的最值,圆锥的侧面展开图为一扇形,这个扇形的 弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.熟记圆锥的侧面积: 1S 2rl rl 是解题的关键. 218. 如图,小明在 3×3 的方格纸上写了九个式子(其中的 n 是正整数),每行的三个式子的 和自上而下分别记为 A1,A2,A3,每列的三个式子的和自左至右分别记为 B1,B2,B3,其 中,值可以等于 789 的是( )A. A1 B. B1 C. A2 D. B3 【答案】B 【解析】 【分析】把 A1,A2,B1,B3 的式子表示出来,再结合值等于 789,可求相应的 n 的值,即可 判断. 【详解】解:由题意得:A1=2n+1+2n+3+2n+5=789, 整理得:2n=260, 则 n 不是整数,故 A1 的值不可以等于 789; A2=2n+7+2n+9+2n+11=789, 整理得:2n=254, 则 n 不是整数,故 A2 的值不可以等于 789; B1=2n+1+2n+7+2n+13=789, 整理得:2n=256=28, 则 n 是整数,故 B1 的值可以等于 789; B3=2n+5+2n+11+2n+17=789, 整理得:2n=252, 则 n 不是整数,故 B3 的值不可以等于 789; 故选:B. 【点睛】本题主要考查规律型:数字变化类,解答的关键是理解清楚题意,得出相应的式 子. 三、解答题(本大题共 10 小题,解答时应写出文字说明、证明过程或演算步骤) 19. (1)计算:(1﹣ )0﹣2sin45°+ ;221(2)化简:(x2﹣1)÷(1﹣ )﹣x. x【答案】(1)1;(2)x2 【解析】 【分析】(1)根据零指数幂的意义、特殊角的锐角三角函数值即可求出答案. (2)根据分式的加减运算以及乘除运算法则即可求出答案. 【详解】解:(1)(1﹣ )0﹣2sin45°+ 222﹣=1 2× 2 2=1. 1(2)(x2﹣1)÷(1﹣ )﹣x x=(x+1)(x﹣1)÷ x 1 ﹣x xx=(x+1)(x﹣1)• ﹣x x 1 =x(x+1)﹣x =x2. 【点睛】本题考查整式的运算以及分式的运算,解题的关键是熟练运用整式的加减运算以及 乘除运算法则. 3220. (1)解方程: ﹣=0; xx 2 3x 1 x 1 x 4 4x 2 (2)解不等式组: .【答案】(1)x=6;(2)x>2 【解析】 【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到 x 的值,经检验即可 得到分式方程的解; (2)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集 即可. 32【详解】解:(1) ﹣=0 xx 2 去分母得:3(x﹣2)﹣2x=0, 去括号得:3x﹣6﹣2x=0, 解得:x=6, 检验:把 x=6 代入得:x(x﹣2)=24≠0, ∴分式方程的解为 x=6; 3x 1 x 1 ① (2) ,x 4 4x 2 ② 由①得:x≥1, 由②得:x>2, 则不等式组的解集为 x>2. 【点睛】此题考查了解分式方程,以及解一元一次不等式组,熟练掌握分式方程的解法以及 不等式组的解法是解本题的关键. 21. 甲、乙、丙三人各自随机选择到 A,B 两个献血站进行爱心献血.求这三人在同一个献 血站献血的概率. 1【答案】 4【解析】 【分析】首先根据题意画树状图,然后根据树状图即可求得所有等可能的结果和满足条件的 结果数,再根据概率公式求解即可. 【详解】解:画树状图得: 共 8 种等可能情况,其中这三人在同一个献血站献血的有 2 种结果, 2814所以这三人在同一个献血站献血的概率为 .【点睛】此题考查了树状图法求概率.注意树状图法适台两步或两步以上完成的事件,树状 图法可以不重不漏的表示出所有等可能的结果,用到的知识点为:概率=所求情况数与总情 况数之比. 22. 如图,四边形 ABCD 是平行四边形,延长 DA,BC,使得 AE=CF,连接 BE,DF. (1)求证: ;△ABE≌△CDF (2)连接 BD,∠1=30°,∠2=20°,当∠ABE= °时,四边形 BFDE 是菱形. 【答案】(1)见解析;(2)当∠ABE=10°时,四边形 BFDE 是菱形 【解析】 【分析】(1)根据平行四边形的性子和“SAS”可证△ABE≌△CDF; (2)先证明四边形 BFDE 是平行四边形,再通过证明 BE=DE,可得结论. 【详解】解:(1)证明:∵四边形 ABCD 是平行四边形, ∴AB=CD,∠BAD=∠BCD, ∴∠1=∠DCF, 在△ABE 和△CDF 中, AE CF 1 DCF AB CD ,∴△ABE≌△CDF(SAS); (2)当∠ABE=10°时,四边形 BFDE 是菱形, 理由如下:∵△ABE≌△CDF, ∴BE=DF,AE=CF, ∴BF=DE, ∴四边形 BFDE 是平行四边形, ∵∠1=30°,∠2=20°, ∴∠ABD=∠1-∠2=10°, ∴∠DBE=20°, ∴∠DBE=∠EDB=20°, ∴BE=DE, ∴平行四边形 BFDE 是菱形, 故答案为 10. 【点睛】本题考查了菱形的判定,平行四边形的判定和性质,全等三角形的判定和性质,掌 握菱形的判定是解题的关键. 的23. 《九章算术》被历代数学家尊为“算经之首”.下面是其卷中记载 关于“盈不足”的 一个问题:今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何? 这段话的意思是:今有人合伙买金,每人出 400 钱,会剩余 3400 钱;每人出 300 钱,会剩 余 100 钱.合伙人数、金价各是多少?请解决上述问题. 【答案】共 33 人合伙买金,金价为 9800 钱 【解析】 【分析】设共 x 人合伙买金,金价为 y 钱,根据“每人出 400 钱,会剩余 3400 钱;每人出 300 钱,会剩余 100 钱”,即可得出关于 x,y 的二元一次方程组,解之即可得出结论. 【详解】解:设共 x 人合伙买金,金价为 y 钱, 400x 3400 y 300x 100 y 依题意得: ,x 33 解得: .y 9800 答:共 33 人合伙买金,金价为 9800 钱. 【点睛】本题考查了二元-次方程组的应用以及数学常识,找准等量关系,正确列出二元一 次方程组是解题的关键. 24. 如表是第四至七次全国人口普查的相关数据. 我国大陆人口 总数 其中具有大学文 化程度的人数 每 10 万大陆人口中具 年份 有大学文化程度的人数 1990 年 1133682501 16124678 1422 2000 年 2010 年 2020 年 1265830000 1339724852 1411778724 45710000 119636790 218360767 3611 8930 15467 的(1)设下一次人口普查我国大陆人口共 a 人,其中具有大学文化程度 有b 人,则该次人 口普查中每 10 万大陆人口中具有大学文化程度的人数为 ;(用含有 a,b 的代数式表示) (2)如果将 2020 年大陆人口中具有各类文化程度(含大学、高中、初中、小学、其他)的 人数分布制作成扇形统计图,求其中表示具有大学文化程度类别的扇形圆心角的度数;(精 确到 1°) (3)你认为统计“每 10 万大陆人口中具有大学文化程度的人数”这样的数据有什么好处? (写出一个即可) 100000b 【答案】(1) ;(2)56°;(3)比较直观的反应出“每 10 万大陆人口中具有大学 a文化程度的人数”的大小,说明国民素质和文化水平的情况 【解析】 【分析】(1)根据“每 10 万大陆人口中具有大学文化程度的人数”的意义求解即可; (2)求出 2020 年,“具有大学文化程度的人数”所占总人数的百分比,即可求出相应的圆 心角度数; (3)根据“每 10 万大陆人口中具有大学文化程度的人数”的实际意义得出结论. 【详解】解:(1)由题意得,下一次人口普查中每 10 万大陆人口中具有大学文化程度的人 100000b 数为 ,a100000b 故答案为: ;a218360767 (2)360°× ≈56°, 1411778724 答:表示具有大学文化程度类别的扇形圆心角的度数大约为 56°; (3)比较直观的反应出“每 10 万大陆人口中具有大学文化程度的人数”的大小,说明国民 素质和文化水平的情况. 【点睛】本题考查扇形统计图,频数分布表,掌握扇形统计图的制作方法是正确解答的前提, 理解“每 10万大陆人口中具有大学文化程度的人数”的实际意义是正确判断的关键. k25. 如图,点 A 和点 E(2,1)是反比例函数 y= (x>0)图象上的两点,点 B 在反比例函 x6数 y= (x<0)的图象上,分别过点 A,B 作 y 轴的垂线,垂足分别为点 C,D,AC= xBD,连接 AB 交 y 轴于点 F. (1)k= ; (2)设点 A 的横坐标为 a,点 F 的纵坐标为 m,求证:am=﹣2; (3)连接 CE,DE,当∠CED=90°时,直接写出点 A 的坐标: . 6535【答案】(1)2;(2)见解析;(3)( ,)【解析】 【分析】(1)将 E 点坐标代入函数解析式即可求得 k 值; (2)根据 AAS 可证△BDF≌△ACF,根据全等三角形面积相等即可得证结论; 226(3)设 A 点坐标为(a, ),则可得C(0, ),D(0,﹣ ),根据勾股定理求出a 值, aaa即可求得 A 点的坐标. k【详解】解:(1)∵点 E(2,1)是反比例函数 y= (x>0)图象上的点, xk∴=1, 2解得 k=2, 故答案为:2; (2)在△BDF 和△ACF 中, ACF BDF CFA BFD AC BD ,∴△BDF≌△ACF(AAS), ∴S△BDF=S△ACF ,26121即a×( ﹣m)= a×( +m), 2aa整理得 am=﹣2; (3)设 A 点坐标为(a, ), 2a26则 C(0, ),D(0,﹣ ), aa∵E(2,1),∠CED=90°, ∴CE2+DE2=CD2, 2626即 22+(1﹣ )2+22+(1+ )2=( +)2, aaaa65解得 a=﹣2(舍去)或 a= ,6535∴A 点的坐标为( ,). 【点睛】本题主要考查反比例函数的性质,全等三角形的判定和性质,三角形面积等知识, 熟练掌握反比例函数图象上点的特征是解题的关键. 26. 如图 1,正方形 ABCD 的边长为 4,点 P 在边 BC 上,⊙O 经过 A,B,P 三点. (1)若 BP=3,判断边 CD 所在直线与⊙O 的位置关系,并说明理由; (2)如图 2,E 是 CD 的中点,⊙O 交射线 AE 于点 Q,当 AP 平分∠EAB 时,求 tan∠EAP 的值. 5 1 2【答案】(1)相切,见解析;(2) 【解析】 【分析】(1)如图 1 中,连接 AP,过点 O 作 OH⊥AB 于 H,交 CD 于 E.求出 OE 的长, 与半径半径,可得结论. (2)如图 2 中,延长 AE 交 BC 的延长线于 T,连接 PQ.利用面积法求出 BP,可得结论. 【详解】解:(1)如图 1﹣1 中,连接 AP,过点 O 作 OH⊥AB 于 H,交 CD 于 E. ∵四边形 ABCD 是正方形, ∴AB=AD=4,∠ABP=90°, 42 32 AB2 BP2 ∴AP= ==5, ∵OH⊥AB, ∴AH=HB, ∵OA=OP,AH=HB, 321∴OH= PB= ,2∵∠D=∠DAH=∠AHE=90°, ∴四边形 AHED 矩形, 是∴OE⊥CE,EH=AD=4, 352∴OE=EH=OH=4﹣ ∴OE=OP, =,2∴直线 CD 与⊙O 相切. (2)如图 2 中,延长 AE 交 BC 的延长线于 T,连接 PQ. ∵∠D=∠ECT=90°,DE=EC,∠AED=∠TEC, ∴△ADE≌△TCE(ASA), ∴AD=CT=4, ∴BT=BC+CT=4+4=8, ∵∠ABT=90°, 42 82 AB2 BT 2 ∴AT= ==4 ,5∵AP 是直径, ∴∠AQP=90°, ∵PA 平分∠EAB,PQ⊥AQ,PB⊥AB, ∴PB=PQ, 设 PB=PQ=x, ∵S△ABT=S△ABP+S△APT ,121×4×8= ×4 21∴×x+ ×4×x, 52∴x=2 ﹣2, 5PB 5 1 2∴tan∠EAP=tan∠PAB= =.AB 【点睛】本题考查了直线与圆的位置关系,正方形的性质,解直角三角形、相似三角形判定 和性质等知识,解题的关键是掌握切线的证明方法:已知垂直证半径,已知半径证垂直,利 用三角形面积不同的表示方法构建方程解决问题是难点. 27. 将一张三角形纸片 ABC 放置在如图所示的平面直角坐标系中,点 A(﹣6,0),点 B(0, 2),点 C(﹣4,8),二次函数 y=ax2+bx+c(a≠0)的图象经过点 A,B,该抛物线的对称轴经 过点 C,顶点为 D. (1)求该二次函数的表达式及点 D 的坐标; (2)点 M 在边 AC 上(异于点 A,C),将三角形纸片 ABC 折叠,使得点 A 落在直线 AB 上, 且点 M 落在边 BC 上,点 M 的对应点记为点 N,折痕所在直线 l 交抛物线的对称轴于点 P, 然后将纸片展开. ①请作出图中点 M 的对应点 N 和折痕所在直线 l;(要求:尺规作图,不写作法,保留作图 痕迹) ②连接 MP,NP,在下列选项中:A.折痕与 AB 垂直,B.折痕与 MN 的交点可以落在抛物 MN MP 32MN MP 线的对称轴上,C. =,D. =,所有正确选项的序号是 . 22③点 Q 在二次函数 y=ax +bx+c(a≠0)的图象上,当 PDQ∼ PMN 时,求点 Q 的坐标. 164216 3×2 + x 2 【答案】(1)y= ,D(﹣4,﹣ );(2)①见解析;②A,D;③(2, )或 3316 (﹣10, )3【解析】 【分析】(1)利用待定系数法求解即可. (2)①根据要求作出图形即可. ②如图 2 中,设线段 MN 的垂直平分线交抛物线对称轴于 P,交 MN 于点 Q,过点 M 作 MH⊥CD,过点 Q 作 QJ⊥CD 于 J,QT⊥MH 于 T.想办法证明△PMN 是等腰直角三角形, 可得结论. ③设 P(﹣4,m).由△PDQ∽△PMN,△PMN 是等腰直角三角形,推出△PDQ 是等腰直角 210 3三角形,推出∠DPQ=90°,DP=PQ=m+ ,推出 Q(﹣ +m,m),构建方程求出 m 即 3可. 【详解】解(1)∵二次函数 y=ax2+bx+c(a≠0)的图象经过点 A(﹣6,0),点 B(0,2),且 抛物线的对称轴经过点 C(﹣4,8), 36a 6b 2 0 c 2 ∴,b 4 2a 14a ,b ,c 2. 解之得: ,63,114×2 + x 2 ∴y= 63423(4)2 (4) 2 ∴当 x=﹣4 时,y= =﹣ ,632∴D(﹣4,﹣ ). 3(2)①如图 1 中,点 N,直线 l 即为所求. ②如图 2 中,设线段 MN 的垂直平分线交抛物线对称轴于 P,交 MN 于点 Q,过点 M 作 MH⊥CD,过点 Q 作 QJ⊥CD 于 J,QT⊥MH 于 T. 由题意 A(﹣6,0),B(0,2),C(﹣4,8), 1∴直线 AC 的解析式为 y=4x+24,直线 AB 的解析式为 y= x+2,直线 BC 的解析式为 y=﹣ 332x+2, ∵MN∥AB, 1∴可以假设直线 MN 的解析式为 y= x+t, 33t 72 11 12t 24 11 1x y y x t 由3,解得 ,y 4x 24 3t 72 12t 24 ∴M( ,), 11 11 312 6t 11 y x 2 x 2由.解得 ,14 9t 11 y x t y 312 6t 4 9t ∴N( ,), 11 11 60 3t 21t 20 ∴Q(( ,), 22 22 ∵QJ⊥CD,QT⊥MH, 60 3t 283t 22 21t 20 24t 48 283t ∴QJ= +4= ,QT= ﹣=,22 22 22 22 ∴QJ=QT, ∵∠PJQ=∠MTQ=90°,∠QPJ=∠QMT,QJ=QT, ∴△PJQ≌△MTQ(AAS), ∴PQ=MQ, ∵∠PQM=90°, ∴∠PMN=∠MPQ=45°, ∵PM=PN, ∴∠PMN=∠PNM=45°, ∴∠MPN=90°, ∴△PMN 是等腰直角三角形, MN ∴=,故选项 D 正确,B,C 错误, 2MP ∵将三角形纸片 ABC 折叠,使得点 A 落在直线 AB 上,且点 M 落在边 BC 上, ∴折痕与 AB 垂直,故选项 A 正确, 故答案为:A,D. ③设 P(﹣4,m). ∵△PDQ∽△PMN,△PMN 是等腰直角三角形, ∴△PDQ 是等腰直角三角形, 2∴∠DPQ=90°,DP=PQ=m+ ,3210 3∴Q(﹣4+m+ ,m),即 Q(﹣ +m,m), 314110 410 y x2 x 2 m ( m)2 + ( m) 2 把 Q 的坐标代入 ,得到, ,636333整理得,9m2﹣42m﹣32=0, 16 32解得 m= 或﹣ (舍弃), 316 ∴Q(2, ), 316 根据对称性可知 Q′(﹣10, )也满足条件, 316 16 3综上所述,满足条件的点 Q 的坐标为(2, )或(﹣10, ). 3【点睛】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,等腰直角三 角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会利用参数解决问题, 证明△PMN 是等腰直角三角形是本题的突破点. 28. 如图 1,∠A=∠B=∠C=∠D=∠E=∠F=90°,AB,FE,DC 为铅直方向的边,AF, ED,BC 为水平方向的边,点 E 在 AB,CD 之间,且在 AF,BC 之间,我们称这样的图形 为“L 图形”,记作“L 图形 ABC﹣DEF”.若直线将 L 图形分成面积相等的两个图形,则称 这样的直线为该 L 图形的面积平分线. 【活动】 小华同学给出了图 1 的面积平分线的一个作图方案:如图 2,将这个 L 图形分成矩形 AGEF、矩形 GBCD,这两个矩形的对称中心 O1,O2 所在直线是该 L 图形的面积平分线.请 用无刻度的直尺在图 1 中作出其他的面积平分线.(作出一种即可,不写作法,保留作图痕 迹) 【思考】 如图 3,直线 O1O2 是小华作的面积平分线,它与边 BC,AF 分别交于点 M,N,过 MN 的中 点 O 的直线分别交边 BC,AF 于点 P,Q,直线 PQ (填“是”或“不是”)L 图形 ABCDEF 的面积平分线. 【应用】 在 L 图形 ABCDEF 形中,已知 AB=4,BC=6. (1)如图 4,CD=AF=1. ①该 L 图形的面积平分线与两条水平的边分别相交于点 P,Q,求 PQ 长的最大值; ②该 L 图形的面积平分线与边 AB,CD 分别相交于点 G,H,当 GH 的长取最小值时,BG 的长为 . CD (2)设 =t(t>0),在所有的与铅直方向的两条边相交的面积平分线中,如果只有与 AF 边 AB,CD 相交的面积平分线,直接写出 t 的取值范围 . 3123【答案】【活动】见解析;【思考】是;【应用】(1)① ;② ;(2) <t< 543【解析】 【分析】[活动]如图 1,根据题意把原本图形分成左右两个矩形,这两个矩形的对称中心 O1,O2 所在直线是该 L 图形的面积平分线; [思考]如图 2,证明△OQN≌△OPM(AAS),根据割补法可得直线 PQ 是 L 图形 ABCDEF 的面积平分线; [应用] (1)①建立平面直角坐标系,分两种情况:如图 3﹣1 和 3﹣2,根据中点坐标公式和待定 系数法可得面积平分线的解析式,并计算 P 和 Q 的坐标,利用两点的距离公式可得 PQ 的 长,并比较大小可得结论; ②当 GH⊥AB 时,GH 最小,设 BG=x,根据面积相等列方程,解出即可; (2)如图 5,由已知得:CD=tAF,直线 DE 将图形分成上下两个矩形,当上矩形面积小于 下矩形面积时,在所有的与铅直方向的两条边相交的面积平分线中,只有与边 AB,CD 相 交的面积平分线,列不等式可得 t 的取值. 【详解】解:【活动】如图 1,直线 O1O2 是该 L 图形的面积平分线; 【思考】如图 2,∵∠A=∠B=90°, ∴AF∥BC, ∴∠NQO=∠MPO, ∵点 O 是 MN 的中点, ∴ON=OM, 在△OQN 和△OPM 中, NQO MPO NOQ MOP ON OW ,∴△OQN≌△OPM(AAS), ∴S△OQN=S△OPM ∵S 梯形 ABMN=SMNFEDC ∴S 梯形 ABMN﹣S△OPM=SMNFEDC﹣S△OQN ,,,即 SABPON=SCDEFQOM ∴SABPON+S△OQN=SCDEFQOM+S△OPM 即 S 梯形 ABPQ=SCDEFQP ,,,∴直线 PQ 是 L 图形 ABCDEF 的面积平分线. 故答案为:是; 【应用】(1)①如图 3﹣1,以直线 OC 为 x 轴,OA 为 y 轴,以 B 为原点,建立平面直角坐 标系,同理确定 L 图形 ABCDEF 的面积平分线:直线 O1O2, ∵AB=4,BC=6,AF=CD=1, ∴B(0,0),F(1,4),D(6,1),K(1,0), 72112∴线段 BF 的中点 O1 的坐标为( ,2),线段 DK 的中点 O2 的坐标为( ,), 2设直线 O1O2 的解析式为:y=kx+b, 127129k b 2 k 则,解得: ,1k b b 2 24941∴直线 O1O2 的解析式为:y=﹣ x+ ,2991当 y=0 时,﹣ x+ =0,解得:x= ,2429∴Q( ,0), 29521当 y=1 时,﹣ x+ =1,解得:x= ,245∴P( ,1), 295( )2 (1 0)2 ∴PQ= =;52 2 如图 3﹣2,同理确定平面直角坐标系,画出 L 图形 ABCDEF 的面积平分线:直线 O3O4, ∵G(0,1),F(1,4),C(6,0), 52121∴线段 GF 的中点 O3 的坐标为( ,),线段 CG 的中点 O4 的坐标为(3, ), 2设直线 O3O4 的解析式为:y=mx+n, 4529 12521m m n 则,解得: ,3m n n 210 429 10 ∴直线 O3O4 的解析式为:y=﹣ x+ ,54当 y=0 时,﹣ x+ 529 10 29 =0,解得:x= ,829 ∴Q( ,0), 8429 10 19 8当 y=1 时,﹣ x+ =1,解得:x= ,519 ∴P( ,1), 829 19 41 )2 (1 0)2 ∴PQ= =;(88441 4∵<;5∴PQ 长的最大值为 ;5②如图 4,当 GH⊥AB 时 GH 最短,过点 E 作 EM⊥AB 于 M, 设 BG=x,则 MG=1﹣x, 根据上下两部分面积相等可知,6x=(4﹣1)×1+(1﹣x)×6, 334解得 x= ,即BG= ;43故答案为: ;4CD AF (2)∵ =t(t>0), ∴CD=tAF, 在所有的与铅直方向的两条边相交的面积平分线中,只有与边 AB,CD 相交的面积平分线, 如图 5,直线 DE 将图形分成上下两个矩形,当上矩形面积小于下矩形面积时,在所有的与 铅直方向的两条边相交的面积平分线中,只有与边 AB,CD 相交的面积平分线, 即(4﹣tAF)•AF<6t•AF, 4AF 6 ∴,t∵0<AF<6, 4∴0< ﹣6<6, t1323 t ∴.123故答案为: <t< .3【点睛】本题是四边形的综合题,考查了应用与设计作图,矩形的性质和判定,四边形面积 的平分,三角形全等的性质和判定等知识,并结合平面直角坐标系计算线段的长,明确面积 平分线的画法,并熟练掌握矩形面积平分线是过对角线交点的性质是解题的关键.
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





