


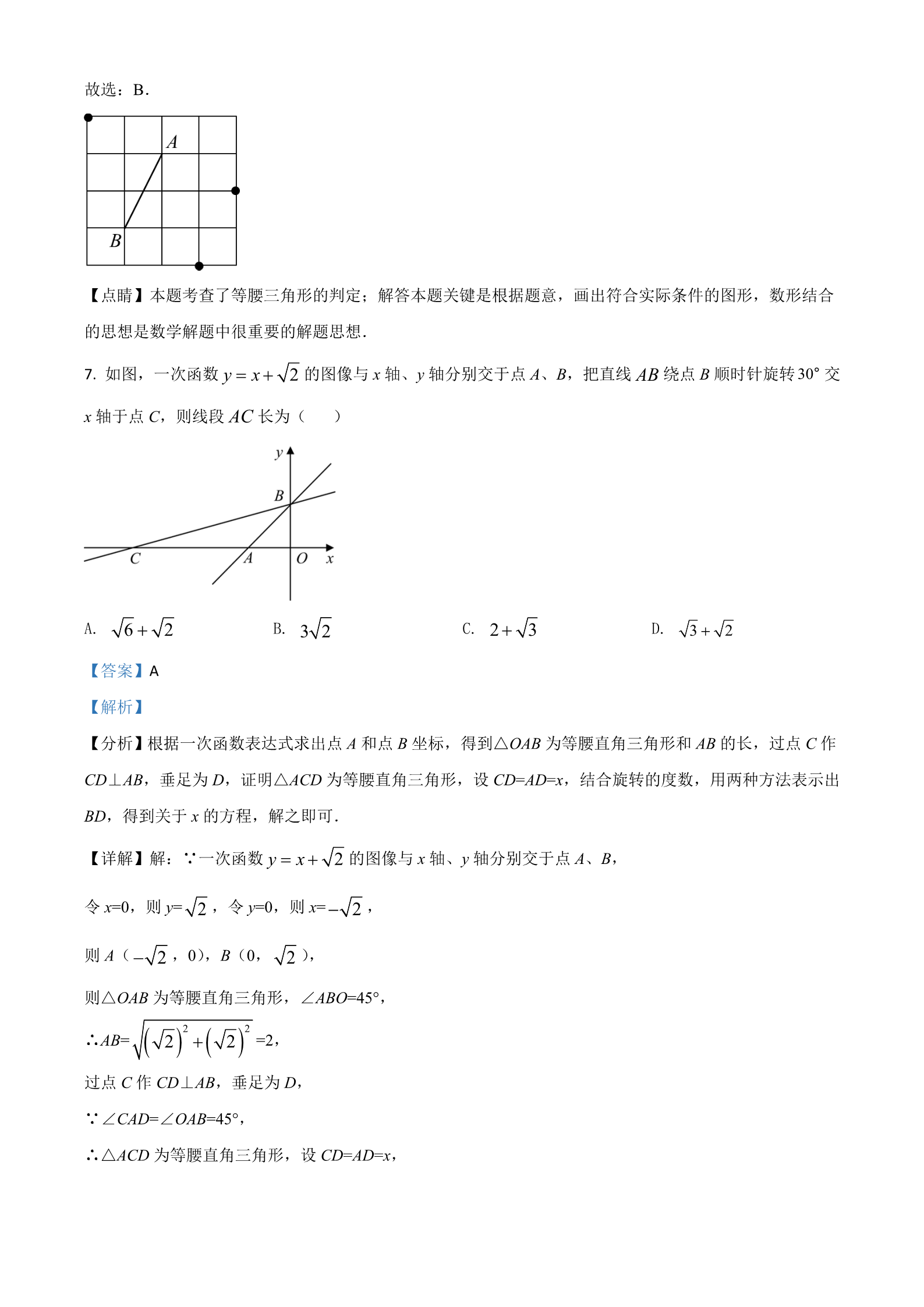
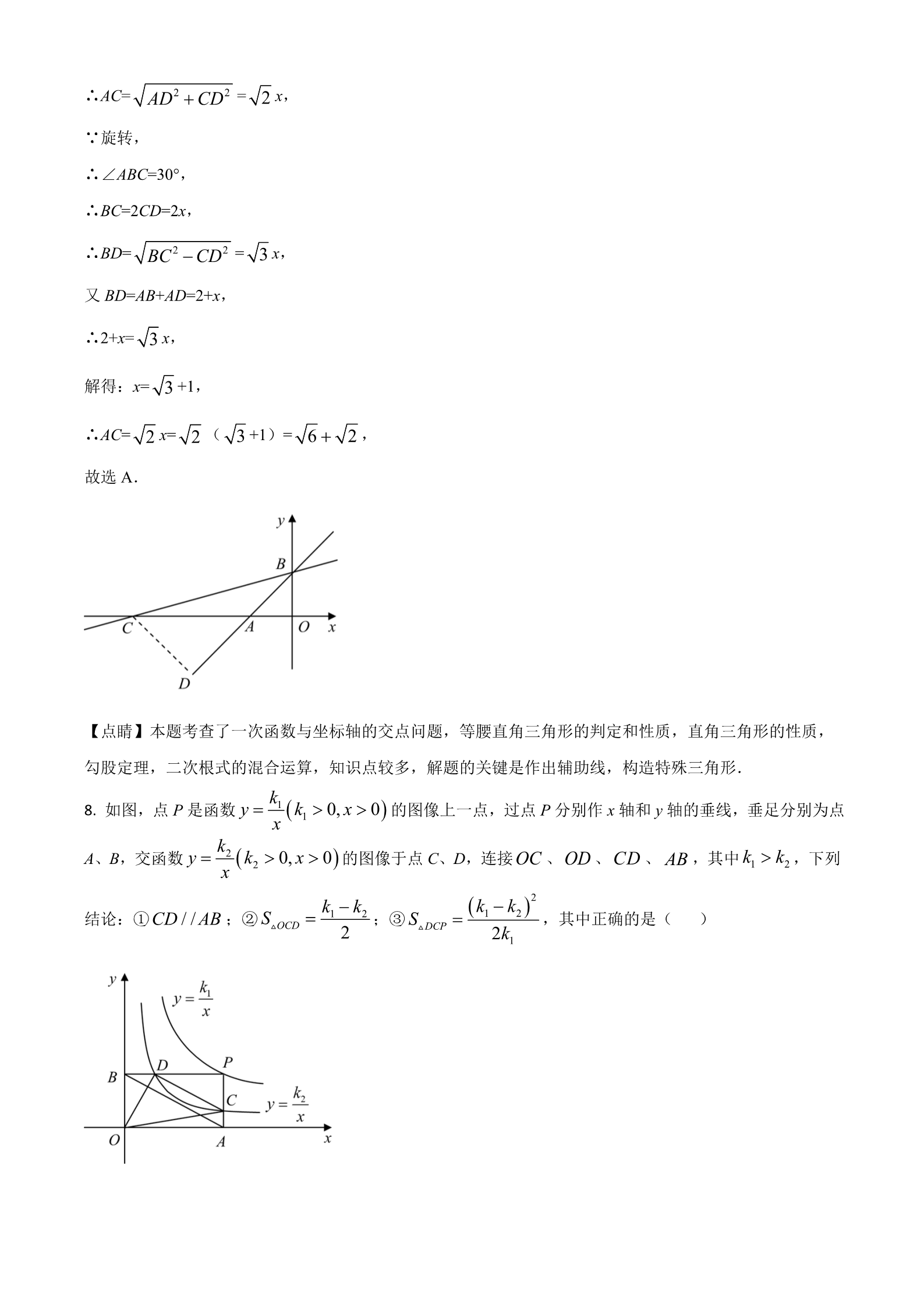
江苏省扬州市 2021 年中考数学试题 一、选择题(本大题共有 8 小题,每小题 3 分,共 24 分.在每小题所给出的四个选项中,恰 有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上) 1. A. 实数 100 的倒数是( )11100 B. C. D. 100 100 100 C【答案】 【解析】 【分析】直接根据倒数的定义求解. 1【详解】解:100 的倒数为 故选 C. ,100 1【点睛】本题考查了倒数的定义:a(a≠0)的倒数为 .a2. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )A. 五棱锥 B. 五棱柱 C. 六棱锥 D. 六棱柱 A【答案】 【解析】 【分析】由平面图形的折叠及立体图形的表面展开图的特点解题. 【详解】解:由图可知:折叠后,该几何体的底面是五边形, 则该几何体为五棱锥, 故选 A. 【点睛】本题考查了几何体的展开图,掌握各立体图形的展开图的特点是解决此类问题的关键. 3. 下列生活中的事件,属于不可能事件的是( )A. 3 天内将下雨 B. 打开电视,正在播新闻 D. 没有水分,种子发芽 C. 买一张电影票,座位号是偶数号 D【答案】 【解析】 【分析】根据事件发生的可能性大小判断即可. 【详解】解:A、3 天内将下雨,是随机事件; B、打开电视,正在播新闻,是随机事件; C、买一张电影票,座位号是偶数号,是随机事件; D、没有水分,种子不可能发芽,故是不可能事件; 故选 D. 【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的 事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可 能发生也可能不发生的事件. 4. 不论 x 取何值,下列代数式的值不可能为 0 的是( B. )12×2 1 A. C. D. x 1 x 1 x 1 C【答案】 【解析】 【分析】分别找到各式为 0 时的 x 值,即可判断. 【详解】解:A、当 x=-1 时,x+1=0,故不合题意; B、当 x=±1 时,x2-1=0,故不合题意; 1C、分子是 1,而 1≠0,则 ≠0,故符合题意; x 1 2D、当 x=-1 时, 故选 C. ,故不合题意; x 1 0 【点睛】本题考查了分式的值为零的条件,代数式的值.若分式的值为零,需同时具备两个条件:(1)分 子为 0;(2)分母不为 0.这两个条件缺一不可. 5. 如图,点 A、B、C、D、E 在同一平面内,连接 、BC 、、、DE EA ,若 ,则 CD BCD 100 AB ()A B D E 260 A. B. C. D. 220 240 280 D【答案】 【解析】 【分析】连接 BD,根据三角形内角和求出∠CBD+∠CDB,再利用四边形内角和减去∠CBD 和∠CDB 的和, 即可得到结果. 【详解】解:连接 BD,∵∠BCD=100°, ∴∠CBD+∠CDB=180°-100°=80°, ∴∠A+∠ABC+∠E+∠CDE=360°-∠CBD-∠CDB=360°-80°=280°, 故选 D. 【点睛】本题考查了三角形内角和,四边形内角和,解题的关键是添加辅助线,构造三角形和四边形. 6. 如图,在 的正方形网格中有两个格点 A、B,连接 ,在网格中再找一个格点 C,使得ABC 是44 AB 等腰直角三角形,满足条件的格点 C 的个数是( )A. 2 B. 3 C. 4 D. 5 B【答案】 【解析】 【分析】根据题意,结合图形,分两种情况讨论:①AB 为等腰直角△ABC 底边;②AB 为等腰直角△ABC 其中的一条腰. 【详解】解:如图:分情况讨论: ①AB 为等腰直角△ABC 底边时,符合条件的 C 点有 0 个; ②AB 为等腰直角△ABC 其中的一条腰时,符合条件的 C 点有 3 个. 故共有 3 个点, 故选:B. 【点睛】本题考查了等腰三角形的判定;解答本题关键是根据题意,画出符合实际条件的图形,数形结合 的思想是数学解题中很重要的解题思想. 30° 交7. 如图,一次函数 的图像与 x 轴、y 轴分别交于点 A、B,把直线 绕点 B 顺时针旋转 AB y x 2 x 轴于点 C,则线段 长为( )AC A. B. C. D. 6 2 2 3 3 2 3 2 A【答案】 【解析】 【分析】根据一次函数表达式求出点 A 和点 B 坐标,得到△OAB 为等腰直角三角形和 AB 的长,过点 C 作 CD⊥AB,垂足为 D,证明△ACD 为等腰直角三角形,设 CD=AD=x,结合旋转的度数,用两种方法表示出 BD,得到关于 x 的方程,解之即可. 【详解】解:∵一次函数 的图像与 x 轴、y 轴分别交于点 A、B, y x 2 令 x=0,则 y= ,令 y=0,则 x= ,2 2 则 A( ,0),B(0, ), 2 2则△OAB 为等腰直角三角形,∠ABO=45°, 22 2∴AB= =2, 2过点 C 作 CD⊥AB,垂足为 D, ∵∠CAD=∠OAB=45°, ∴△ACD 为等腰直角三角形,设 CD=AD=x, AD2 CD2 ∴AC= =x, 2∵旋转, ∴∠ABC=30°, ∴BC=2CD=2x, BC2 CD2 ∴BD= =x, 3又 BD=AB+AD=2+x, ∴2+x= 解得:x= ∴AC= x, 3+1, 3x= (+1)= ,36 2 22故选 A. 【点睛】本题考查了一次函数与坐标轴的交点问题,等腰直角三角形的判定和性质,直角三角形的性质, 勾股定理,二次根式的混合运算,知识点较多,解题的关键是作出辅助线,构造特殊三角形. k1 8. y k 0, x 0 的图像上一点,过点 P 分别作 x 轴和 y 轴的垂线,垂足分别为点 如图,点 P 是函数 1xk2 k k y k 0, x 0 的图像于点 C、D,连接 A、B,交函数 、、、,其中 )2 ,下列 OC OD CD AB 12x2k k k1 k2 2 1S结论:①CD / /AB ;② ;③ SDCP ,其中正确的是( OCD 22k1 A. ①② 【答案】 【解析】 B. ①③ C. ②③ D. ① Bk1 PD PC 【分析】设 P(m, ),分别求出A,B,C,D 的坐标,得到 PD,PC,PB,PA 的长,判断 和PA mPB 的 关 系 , 可 判 断 ① ; 利 用 三 角 形 面 积 公 式 计 算 , 可 得 △PDC 的 面 积 , 可 判 断 ③ ; 再 利 用 S△OCD SOAPB S△OBD S△OCA S △DPC 计算△OCD 的面积,可判断②. k1 xk2 y y 【详解】解:∵PB⊥y 轴,PA⊥x 轴,点 P 在 上,点 C,D 在 上, xk1 设 P(m, ), mk2 k1 k1 k2 则 C(m, ),A(m,0),B(0, ),令 ,mxmmk2m k2m k1 k1 mx 则,即 D( ,), k1 k2m k1 m k k k1 k2 2 ,k1 k2 m1m ∴PC= =,PD= =k1 mmk1 k2 mk1 m k k 2 1k1 k2 k1 PC PD PC k1 mk1 k2 ,k1 ∵PD PB ,即 ,PA PB PA m又∠DPC=∠BPA, ∴△PDC∽△PBA, ∴∠PDC=∠PBC, ∴CD∥AB,故①正确; 2m k k k k 2 k1 k2 1122 11 PD PC △PDC 的面积= ==,故③正确; 2k1 m2k1 S△OCD SOAPB S△OBD S△OCA S△DPC 2k k 2 111===k1 k2 k2 222k1 2k k 2 1k1 k2 2k1 22k k k k k 1 2k1 2 2 112k1 22k 2 2k k k k 2 1121==2k1 2k12 k2 2k1 ,故②错误; 故选 B. 【点睛】此题主要考查了反比例函数的图象和性质,k 的几何意义,相似三角形的判定和性质,解题关键是 表示出各点坐标,得到相应线段的长度. 二、填空题(本大题共有 10 小题,每小题 3 分,共 30 分.不需写出解答过程,请把答案直 接填写在答题卡相应位置上) 9. 2021 年扬州世界园艺博览会以“绿色城市,健康生活”为主题,在某搜索引擎中输入“扬州世界园艺博 览会”约有 3020000 个相关结果,数据 3020000 用科学记数法表示为______. 【答案】3.02×106 【解析】 【分析】科学记数法的表示形式为 a×10n 的形式,其中 1≤|a|<10,n 为整数.确定 n 的值时,要看把原数变 成 a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同. 【详解】解:将 3020000 用科学记数法表示为 3.02×106. 故答案为:3.02×106. 【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为 a×10n 的形式,其中 1≤|a|<10,n 为整 数,表示时关键要正确确定 a 的值以及 n 的值. 2210. 计算: __________. 2021 2020 【答案】4041 【解析】 【分析】利用平方差公式进行简便运算即可. 22【详解】解: 2021 2020 2021 2020 2021 2020 ==40411 =4041 故答案为:4041. 【点睛】本题考查了平方差公式的应用,解题时注意运算顺序. P 1 m,5 2m 在第二象限,则整数 m 的值为_________. 11. 在平面直角坐标系中,若点 【答案】2 【解析】 【分析】根据第二象限的点的横坐标小于 0,纵坐标大于 0 列出不等式组,然后求解即可. 1 m 0 【详解】解:由题意得: ,5 2m 0 51 m 解得: ,2∴整数 m 的值为 2, 故答案为:2. 【点睛】本题考查了点的坐标及解一元一次不等式组,记住各象限内点的坐标的符号是解决的关键. 12. 已知一组数据:a、4、5、6、7 的平均数为 5,则这组数据的中位数是__________. 【答案】5 【解析】 【分析】根据平均数的定义先算出 a 的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位 数. 【详解】解:∵这组数据的平均数为 5, a 4 5 6 7 5 则,5解得:a=3, 将这组数据从小到大重新排列为:3,4,5,6,7, 观察数据可知最中间的数是 5, 则中位数是 5. 故答案为:5. 【点睛】本题考查了平均数和中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后, 最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数. 13. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数 学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日, 问良马几何日追及之?”题意是:快马每天走 240 里,慢马每天走 150 里,慢马先走 12 天,试问快马几天 追上慢马?答:快马_______天追上慢马. 【答案】20 【解析】 【分析】设良马行 x 日追上驽马,根据路程=速度×时间结合两马的路程相等,即可得出关于 x 的一元一次 方程,解之即可得出结论. 【详解】解:设快马行 x 天追上慢马,则此时慢马行了(x+12)日, 依题意,得:240x=150(x+12), 解得:x=20, ∴快马 20 天追上慢马, 故答案为:20. 【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键. 214. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为_____ .10cm cm 【答案】100 【解析】 【分析】根据圆柱体的主视图为边长为 10cm 的正方形,得到圆柱的底面直径和高,从而计算侧面积. 【详解】解:∵果罐的主视图是边长为 10cm 的正方形,为圆柱体, ∴圆柱体的底面直径和高为 10cm, 10 10 ∴侧面积 为=100 ,故答案为:100 .【点睛】本题考查了几何体的三视图,解题的关键是根据三视图得到几何体的相关数据. 15. 如图,在 中, ,点 D 是 的中点,过点 D 作 DE BC ,垂足为点 E,连接 AB RtABC ACB 90 CD 5 BC 8 ,,若 ,则 ________. CD DE 【答案】3 【解析】 【 分 析 】 根 据 直 角 三 角 形 的 性 质 得 到AB=10 , 利 用 勾 股 定 理 求 出AC , 再 说 明DE∥AC , 得 到 DE BD 12,即可求出 DE. AC AB 【详解】解:∵∠ACB=90°,点 D 为 AB 中点, ∴AB=2CD=10, ∵BC=8, AB2 BC2 ∴AC= =6, ∵DE⊥BC,AC⊥BC, ∴DE∥AC, DE BD 12DE BD 12∴,即 ,AC AB 6AB ∴DE=3, 故答案为:3. 【点睛】本题考查了直角三角形的性质,勾股定理,平行线分线段成比例,解题的关键是通过平行得到比 例式. EC 16. 如图,在ABCD 中,点 E 在 的面积为________. 上,且 平分 ,若 EBC 30 BED ,,则ABCD BE 10 AD 【答案】50 【解析】 【分析】过点 E 作 EF⊥BC,垂足为 F,利用直角三角形的性质求出 EF,再根据平行线的性质和角平分线 的定义得到∠BCE=∠BEC,可得 BE=BC=10,最后利用平行四边形的面积公式计算即可. 【详解】解:过点 E 作 EF⊥BC,垂足为 F, ∵∠EBC=30°,BE=10, 1∴EF= BE=5, 2∵四边形 ABCD 是平行四边形, ∴AD∥BC, ∴∠DEC=∠BCE, 又 EC 平分∠BED,即∠BEC=∠DEC, ∴∠BCE=∠BEC, ∴BE=BC=10, BC EF ∴四边形 ABCD 的面积= 故答案为:50. ==50, 105 【点睛】本题考查了平行四边形的性质,30 度的直角三角形的性质,角平分线的定义,等角对等边,知识 点较多,但难度不大,图形特征比较明显,作出辅助线构造直角三角形求出 EF 的长是解题的关键. 17. 如图,在ABC 中, ,矩形 ,则 DEFG 的顶点 D、E 在 上,点 F、G 分别在 BC 、AC 上, AC BC AB 若,,且 的长为________. CF 4 BF 3 DE 2EF EF 12 【答案】 【解析】 57x AB 【分析】根据矩形的性质得到 GF∥AB,证明△CGF∽△CAB,可得 ,证明△ADG≌△BEF,得到 23xAD=BE= ,在△BEF 中,利用勾股定理求出 x 值即可. 4【详解】解:∵DE=2EF,设 EF=x,则 DE=2x, ∵四边形 DEFG 是矩形, ∴GF∥AB, ∴△CGF∽△CAB, GF CF 4472x 47∴∴,即 ,AB CB 4 3 7x AB AB ,2327x 2x x,∴AD+BE=AB-DE= ∵AC=BC, =2∴∠A=∠B,又 DG=EF,∠ADG=∠BEF=90°, ∴△ADG≌△BEF(AAS), 341232xx∴AD=BE= =,222在△BEF 中, ,BE EF BF 2 3x x2 32 ,即412 512 5解得:x= 或(舍), 12 ∴EF= 5,12 5故答案为: .【点睛】本题考查了相似三角形的判定和性质,矩形的性质,勾股定理,全等三角形的判定和性质,等边 对等角,解题的关键是根据相似三角形的性质得到 AB 的长. 18. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所 有能被 3 整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第 33 个数为___________. 【答案】1275 【解析】 【分析】首先得到前 n 个图形中每个图形中的黑色圆点的个数,得到第 n 个图形中的黑色圆点的个数为 n n1 ,再判断其中能被 3 整除的数,得到每 3 个数中,都有 2 个能被 3 整除,再计算出第 33 个能被 3 2整除的数所在组,为原数列中第 50 个数,代入计算即可. 【详解】解:第①个图形中的黑色圆点的个数为:1, 1 2 2 第②个图形中的黑色圆点的个数为: =3, 21 3 3 第③个图形中的黑色圆点的个数为: =6, 21 4 4 第④个图形中的黑色圆点的个数为: =10, 2… n n1 第 n 个图形中的黑色圆点的个数为 ,2则这列数为 1,3,6,10,15,21,28,36,45,55,66,78,91,…, 其中每 3 个数中,都有 2 个能被 3 整除, 33÷2=16…1, 16×3+2=50, 5051 则第 33 个被 3 整除的数为原数列中第 50 个数,即 故答案为:1275. =1275, 2【点睛】此题考查了规律型:图形的变化类,关键是通过归纳与总结,得到其中的规律. 三、解答题(本大题共有 10 小题,共 96 分,请在答题卡指定区域内作答,解答时应写出必 要的文字说明、证明过程或演算步骤) 19. 计算或化简: 0111a b (1) ;(2) . | 3 3| tan60 ab3【答案】(1)4;(2) ab 【解析】 【分析】(1)分别化简各数,再作加减法; (2)先通分,计算加法,再将除法转化为乘法,最后约分计算. 013【详解】解:(1) | 3 3| tan60 =1 3 3 3 =;411ba b (2) aa b ab ab a b =a b ==a b ab 【点睛】本题考查了实数的混合运算,特殊角的三角函数值,零指数幂,分式的混合运算,解题的关键是 熟练掌握运算法则. 2x y 7 x y 1 ax y 4 的一个解,求 a 的值. 20. 已知方程组 的解也是关于 x、y 的方程 1a 【答案】 【解析】 2【分析】求出方程组的解得到 x 与 y 的值,代入方程计算即可求出 a 的值. 2x y 7① 【详解】解:方程组 ,x y 1② 2 y 1 y 7 把②代入①得: ,y 3 解得: 解得: ,代入①中, ,x 2 y 3 ax y 4 得, 把,代入方程 ,x 2 2a 3 4 12a 解得: .【点睛】此题考查了二元一次方程组的解,以及二元一次方程的解,方程组的解即为能使方程组中两方程 成立的未知数的值. 21. 为推进扬州市“青少年茁壮成长工程”,某校开展“每日健身操”活动,为了解学生对“每日健身操” 活动的喜欢程度,随机抽取了部分学生进行调查,将调查信息结果绘制成如下尚不完整的统计图表: 抽样调查各类喜欢程度人数分布扇形统计图 A.非常喜欢 抽样调查各类喜欢程度人数统计表 喜欢程度 人数 B.比较喜欢 C.无所谓 D.不喜欢 50 A.非常喜欢 人B.比较喜欢 m 人 C.无所谓 D.不喜欢 n 人 16 人根据以上信息,回答下列问题: (1)本次调查的样本容量是______; (2)扇形统计图中表示 A 程度的扇形圆心角为_____ m ______; ,统计表中 (3)根据抽样调查的结果,请你估计该校 2000 名学生中大约有多少名学生喜欢“每日健身操”活动(包 含非常喜欢和比较喜欢). 【答案】(1)200;(2)90,94;(3)1440 名 【解析】 【分析】(1)用 D 程度人数除以对应百分比即可; (2)用 A 程度的人数与样本人数的比值乘以 360°即可得到对应圆心角,算出 B 等级对应百分比,乘以样本 容量可得 m 值; (3)用样本中 A、B 程度的人数之和所占样本的比例,乘以全校总人数即可. 【详解】解:(1)16÷8%=200, 则样本容量是 200; 50 (2) ×360°=90°, 200 则表示 A 程度的扇形圆心角为 90°; 50 200×(1-8%-20%- ×100%)=94, 200 则 m=94; 50 94 2000 (3) =1440 名, 200 ∴该校 2000 名学生中大约有 1440 名学生喜欢“每日健身操”活动. 【点睛】本题考查了扇形统计图,统计表,样本估计总体等知识,读懂统计图,从不同的统计图中得到必 要的信息是解决问题的关键,扇形统计图直接反映部分占总体的百分比大小. 22. 一张圆桌旁设有 4 个座位,丙先坐在了如图所示的座位上,甲、乙 2 人等可能地坐到①、②、③中的 2 个座位上. (1)甲坐在①号座位的概率是_________; (2)用画树状图或列表的方法,求甲与乙相邻而坐的概率. 123【答案】(1) ;(2) 3【解析】 【分析】(1)直接根据概率公式计算即可; (2)画树状图,共有 6 种等可能的结果,甲与乙相邻而坐的结果有 4 种,再由概率公式求解即可. 【详解】解:(1)∵丙坐了一张座位, 1∴甲坐在①号座位的概率是 ;3(2)画树状图如图: 共有 6 种等可能的结果,甲与乙两同学恰好相邻而坐的结果有 4 种, 4 2 ∴甲与乙相邻而坐的概率为 =.6 3 【点睛】本题考查了列表法与树状图法求概率,用到的知识点为:概率=所求情况数与总情况数之比. 23. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了 20%,现在 生产 240 万剂疫苗所用的时间比原先生产 220 万剂疫苗所用的时间少 0.5 天,问原先每天生产多少万剂疫 苗? 【答案】40 万 【解析】 【分析】设原先每天生产 x 万剂疫苗,根据现在生产 240 万剂疫苗所用的时间比原先生产 220 万剂疫苗所 用的时间少 0.5 天可得方程,解之即可. 【详解】解:设原先每天生产 x 万剂疫苗, 240 220 0.5 由题意可得: ,1 20% x x解得:x=40, 经检验:x=40 是原方程的解, ∴原先每天生产 40 万剂疫苗. 【点睛】此题主要考查了分式方程的应用,列分式方程解应用题的一般步骤:设、列、解、验、答.必须 严格按照这 5 步进行做题,规范解题步骤,另外还要注意完整性. BAC DE / /AB, DF / /AC .24. 如图,在ABC 中, 的角平分线交 BC 于点 D, (1)试判断四边形 (2)若 的形状,并说明理由; ,求四边形 AFDE ,且 的面积. BAC 90 AFDE AD 2 2 【答案】(1)菱形,理由见解析;(2)4 【解析】 【分析】(1)根据 DE∥AB,DF∥AC 判定四边形 AFDE 是平行四边形,再根据平行线的性质和角平分线的 定义得到∠EDA=∠EAD,可得 AE=DE,即可证明; (2)根据∠BAC=90°得到菱形 AFDE 是正方形,根据对角线 AD 求出边长,再根据面积公式计算即可. 【详解】解:(1)四边形 AFDE 是菱形,理由是: ∵DE∥AB,DF∥AC, ∴四边形 AFDE 是平行四边形, ∵AD 平分∠BAC, ∴∠FAD=∠EAD, ∵DE∥AB, ∴∠EDA=∠FAD, ∴∠EDA=∠EAD, ∴AE=DE, ∴平行四边形 AFDE 是菱形; (2)∵∠BAC=90°, ∴四边形 AFDE 是正方形, ∵AD= ,2 2 2 2 2∴AF=DF=DE=AE= =2, ∴四边形 AFDE 的面积为 2×2=4. 【点睛】本题考查了菱形的判定,正方形的判定和性质,平行线的性质,角平分线的定义,解题的关键是 掌握特殊四边形的判定方法. 25. AD / /BC ,如图,四边形 中, ,BAD 90 CB CD ,连接 ,以点 B 为圆心, 长ABCD BD BA B 为半径作 ,交 于点 E. BD B (1)试判断 (2)若 与的位置关系,并说明理由; ,求图中阴影部分的面积. CD ,BCD 60 AB 2 3 【答案】(1)相切,理由见解析;(2) 2 3 【解析】 【分析】(1)过点 B 作 BF⊥CD,证明△ABD≌△FBD,得到 BF=BA,即可证明 CD 与圆 B 相切; (2)先证明△BCD 是等边三角形,根据三线合一得到∠ABD=30°,求出 AD,再利用 S△ABD-S 扇形 ABE 求出 阴影部分面积. 【详解】解:(1)过点 B 作 BF⊥CD, ∵AD∥BC, ∴∠ADB=∠CBD, ∵CB=CD, ∴∠CBD=∠CDB, ∴∠ADB=∠CDB,又 BD=BD,∠BAD=∠BFD=90°, ∴△ABD≌△FBD(AAS), ∴BF=BA,则点 F 在圆 B 上, ∴CD 与圆 B 相切; (2)∵∠BCD=60°,CB=CD, ∴△BCD 是等边三角形, ∴∠CBD=60° ∵BF⊥CD, ∴∠ABD=∠DBF=∠CBF=30°, ∴∠ABF=60°, ∵AB=BF= ∴AD=DF= ,2 3 AB tan30 =2, ∴阴影部分的面积=S△ABD-S 扇形 ABE 230 2 3 12== 2 3 2 360 .2 3 【点睛】本题考查了切线的判定,全等三角形的判定和性质,等边三角形的判定和性质,扇形面积,三角 函数的定义,题目的综合性较强,难度不小,解题的关键是正确做出辅助线. 如图,在平面直角坐标系中,二次函数 y x2 bx c 的图像与 x 轴交于点. 、A 1,0 B 3,0 ,与 26. y 轴交于点 C. c (1)b ________, ________; S 2SABC ,求点 D 的坐标; (2)若点 D 在该二次函数的图像上,且 ABD S SAPB (3)若点 P 是该二次函数图像上位于 x 轴上方的一点,且 ,直接写出点 P 的坐标. APC 【答案】(1)-2,-3;(2)( ,6)或( ,6);(3)(4,5) 1 10 1 10 【解析】 【分析】(1)利用待定系数法求解即可; (2)先求出△ABC 的面积,设点 D(m, 可求出点 D 的坐标; 2S 2SABC ,得到方程求出 m 值,即 ),再根据 m 2m 3 ABD (3)分点 P 在点 A 左侧和点 P 在点 A 右侧,结合平行线之间的距离,分别求解. 【详解】解:(1)∵点 A 和点 B 在二次函数 y x2 bx c 图像上, 0 1b c b 2 c 3 则,解得: ,0 9 3b c 故答案为:-2,-3; (2)连接 BC,由题意可得: 2A(-1,0),B(3,0),C(0,-3), ,y x 2x 3 143 =6, ∴S△ABC =22∵S△ABD=2S△ABC,设点 D(m, ), m 2m 3 1212 AB yD 2 6 4 m2 2m 3 2 6 ,∴,即 解得:x= 或1 10 1 10 ,代入 y x2 2x 3 ,可得:y 值都为 6, ∴D( ,6)或( ,6); 1 10 1 10 2(3)设 P(n, ), n 2n 3 ∵点 P 在抛物线位于 x 轴上方的部分, ∴n<-1 或 n>3, 当点 P 在点 A 左侧时,即 n<-1, 可知点 C 到 AP 的距离小于点 B 到 AP 的距离, S S ∴△APB ,不成立; △APC 当点 P 点 B 右侧时,即 n>3, 在∵△APC 和△APB 都以 AP 为底,若要面积相等, 则点 B 和点 C 到 AP 的距离相等,即 BC∥AP, 设直线 BC 的解析式为 y=kx+p, 0 3k p 3 p k 1 则,解得: ,p 3 则设直线 AP 的解析式为 y=x+q,将点 A(-1,0)代入, 则-1+q=0,解得:q=1, 2则直线 AP 的解析式为 y=x+1,将 P(n, )代入, n 2n 3 2即,n 2n 3 n 1 解得:n=4 或 n=-1(舍), 2,n 2n 3 5 ∴点 P 的坐标为(4,5). 【点睛】本题考查了二次函数综合,涉及到待定系数法求函数解析式,三角形面积,平行线之间的距离, 一次函数,解题的难点在于将同底的三角形面积转化为点到直线的距离. 27. 在一次数学探究活动中,李老师设计了一份活动单: 已知线段 ,使用作图工具作,尝试操作后思考: BC 2 BAC 30 (1)这样的点 A 唯一吗? (2)点 A 的位置有什么特征?你有什么感悟? “追梦”学习小组通过操作、观察、讨论后汇报:点 A 的位置不唯一,它在以 BC 为弦的圆弧上(点 B、C 除外),…….小华同学画出了符合要求的一条圆弧(如图 1). (1)小华同学提出了下列问题,请你帮助解决. ①该弧所在圆的半径长为___________; ②ABC 面积的最大值为_________; (2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图 1 所示的弓形内部,我们 记为 A,请你利用图 1 证明BA C 30 ;(3)请你运用所学知识,结合以上活动经验,解决问题:如图 2,已知矩形 的边长 ,ABCD AB 2 4tanDPC ,点 P 在直线 的左侧,且 .BC 3 CD 3①线段 PB 长的最小值为_______; 2S SPAD ②若 ,则线段 长为________. PD PCD 397 5 47 2 4【答案】(1)①2;② ;(2)见解析;(3)① ;② 3 2 【解析】 【分析】(1)①设 O 为圆心,连接 BO,CO,根据圆周角定理得到∠BOC=60°,证明△OBC 是等边三角形, 可得半径; ②过点 O 作 BC 的垂线,垂足为 E,延长 EO,交圆于 D,以 BC 为底,则当 A 与 D 重合时,△ABC 的面积 最大,求出 OE,根据三角形面积公式计算即可; (2)延长 BA′,交圆于点 D,连接 CD,利用三角形外角的性质和圆周角定理证明即可; 431tanDPC (3)①根据 ,连接 PD,设点 Q 为 PD 中点,以点 Q 为圆心, PD 为半径画圆,可得点 P 2在优弧 CPD 上,连接 BQ,与圆 Q 交于 P′,可得 BP′即为 BP 的最小值,再计算出 BQ 和圆 Q 的半径,相减 即可得到 BP′; 2S SPAD ②根据 AD,CD 和 推出点 P 在∠ADC 的平分线上,从而找到点 P 的位置,过点 C 作 PCD 3CF⊥PD,垂足为 F,解直角三角形即可求出 DP. 【详解】解:(1)①设 O 为圆心,连接 BO,CO, ∵∠BAC=30°, ∴∠BOC=60°,又 OB=OC, ∴△OBC 是等边三角形, ∴OB=OC=BC=2,即半径为 2; ②∵△ABC 以 BC 为底边,BC=2, ∴当点 A 到 BC 的距离最大时,△ABC 的面积最大, 如图,过点 O 作 BC 的垂线,垂足为 E,延长 EO,交圆于 D, ∴BE=CE=1,DO=BO=2, BO2 BE2 ∴OE= ∴DE= =,3,3 2 12 2 3 2 ∴△ABC 的最大面积为 =;3 2 (2)如图,延长 BA′,交圆于点 D,连接 CD, ∵点 D 在圆上, ∴∠BDC=∠BAC, ∵∠BA′C=∠BDC+∠A′CD, ∴∠BA′C>∠BDC, ∴∠BA′C>∠BAC,即∠BA′C>30°; 3(3)①如图,当点 P 在 BC 上,且 PC= 时, 2∵∠PCD=90°,AB=CD=2,AD=BC=3, 43CD PC ∴tan∠DPC= =,为定值, 1连接 PD,设点 Q 为 PD 中点,以点 Q 为圆心, PD 为半径画圆, 24∴当点 P 在优弧 CPD 上时,tan∠DPC= ,连接 BQ,与圆 Q 交于 P′, 3此时 BP′即为 BP 的最小值,过点 Q 作 QE⊥BE,垂足为 E, ∵点 Q 是 PD 中点, 3411∴点 E 为 PC 中点,即 QE= CD=1,PE=CE= PC= ,223494∴BE=BC-CE=3- =,97 4∴BQ= BE2 QE2 =,,5CD2 PC2 ∵PD= =,21 5 5 ∴圆 Q 的半径为 ∴BP′=BQ-P′Q= 2 2 497 5 97 5 4的,即 BP 最小值为 ;42S SPAD ②∵AD=3,CD=2, ,PCD 3CD AD 23则,∴△PAD 中 AD 边上的高=△PCD 中 CD 边上的高, 即点 P 到 AD 的距离和点 P 到 CD 的距离相等, 则点 P 到 AD 和 CD 的距离相等,即点 P 在∠ADC 的平分线上,如图, 过点 C 作 CF⊥PD,垂足 ∵PD 平分∠ADC, 为F, ∴∠ADP=∠CDP=45°, ∴△CDF 为等腰直角三角形,又 CD=2, 2∴CF=DF= =,22CF PF 4∵tan∠DPC= =,33 2 ∴PF= ,43 27 2 =∴PD=DF+PF= 2 .44【点睛】本题是圆的综合题,考查了圆周角定理,三角形的面积,等边三角形的判定和性质,最值问题, 解直角三角形,三角形外角的性质,勾股定理,知识点较多,难度较大,解题时要根据已知条件找到点 P 的轨迹. 28. 甲、乙两汽车出租公司均有 50 辆汽车对外出租,下面是两公司经理的一段对话: 甲公司经理:如果我公司每辆汽车月租费 3000 元,那么 50 辆汽车可以全部租出.如果每辆汽车的月租费 每增加 50 元,那么将少租出 1辆汽车.另外,公司为每辆租出的汽车支付月维护费 200 元. 乙公司经理:我公司每辆汽车月租费 3500 元,无论是否租出汽车,公司均需一次性支付月维护费共计 1850 元. 说明:①汽车数量为整数; ②月利润=月租车费-月维护费; ③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润. 在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题: (1)当每个公司租出的汽车为 10 辆时,甲公司的月利润是_______元;当每个公司租出的汽车为_______ 辆时,两公司的月利润相等; (2)求两公司月利润差的最大值; a 0 (3)甲公司热心公益事业,每租出 1 辆汽车捐出 a 元 给慈善机构,如果捐款后甲公司剩余的月利 润仍高于乙公司月利润,且当两公司租出的汽车均为 17 辆时,甲公司剩余的月利润与乙公司月利润之差最 大,求 a 的取值范围. 50 a 150 【答案】(1)48000,37;(2)33150 元;(3) 【解析】 【分析】(1)用甲公司未租出的汽车数量算出每辆车的租金,再乘以 10,减去维护费用可得甲公司的月利 润;设每个公司租出的汽车为 x 辆,根据月利润相等得到方程,解之即可得到结果; (2)设两公司的月利润分别为 y 甲,y 乙,月利润差为 y,同(1)可得 y 甲和 y 乙的表达式,再分甲公司的利 润大于乙公司和甲公司的利润小于乙公司两种情况,列出 y 关于 x 的表达式,根据二次函数的性质,结合 x 的范围求出最值,再比较即可; y 50×2 1800 a x1850 (3)根据题意得到利润差为 ,得到对称轴,再根据两公司租出的汽车均为 17 1800 a 16.5 17.5 辆,结合 x 为整数可得关于 a 的不等式 ,即可求出 a 的范围. =48000 元, 当每个公司租出的汽车为 10 辆时,甲公司的月利润是 48000 元; 100 50 10 50 3000 10 20010 【详解】解:(1) 的设每个公司租出 汽车为x 辆, 50 x 50 3000 x 200x 3500x 1850 由题意可得: ,解得:x=37 或 x=-1(舍), ∴当每个公司租出的汽车为 37 辆时,两公司的月利润相等; (2)设两公司的月利润分别为 y 甲,y 乙,月利润差为 y, 50 x 50 3000 x 200x 则 y 甲= ,3500x 1850 y 乙= ,当甲公司的利润大于乙公司时,0<x<37, 50 x 50 3000 x 200x 3500x 1850 y=y 甲-y 乙= 2=,50x 1800x 1850 1800 当 x= =18 时,利润差最大,且为 18050 元; 50 2 当乙公司的利润大于甲公司时,37<x≤50, 3500x 1850 50 x 50 3000 x 200x y=y 乙-y 甲= 2=,50x 1800x 1850 1800 50 2 ∵对称轴为直线 x= =18, 当 x=50 时,利润差最大,且为 33150 元; 综上:两公司月利润差的最大值为 33150 元; (3)∵捐款后甲公司剩余的月利润仍高于乙公司月利润, 50×2 1800 a x1850 ,y 50×2 1800x 1850 ax 则利润差为 =1800 a 对称轴为直线 x= ,100 ∵x 只能取整数,且当两公司租出的汽车均为 17 辆时,月利润之差最大, 1800 a 16.5 17.5 ,∴100 50 a 150 解得: .【点睛】本题考查了二次函数的实际应用,二次函数的图像和性质,解题时要读懂题意,列出二次函数关 系式,尤其(3)中要根据 x 为整数得到 a 的不等式.
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





