精品解析：湖北省宜昌市2020年中考数学试题（解析版）

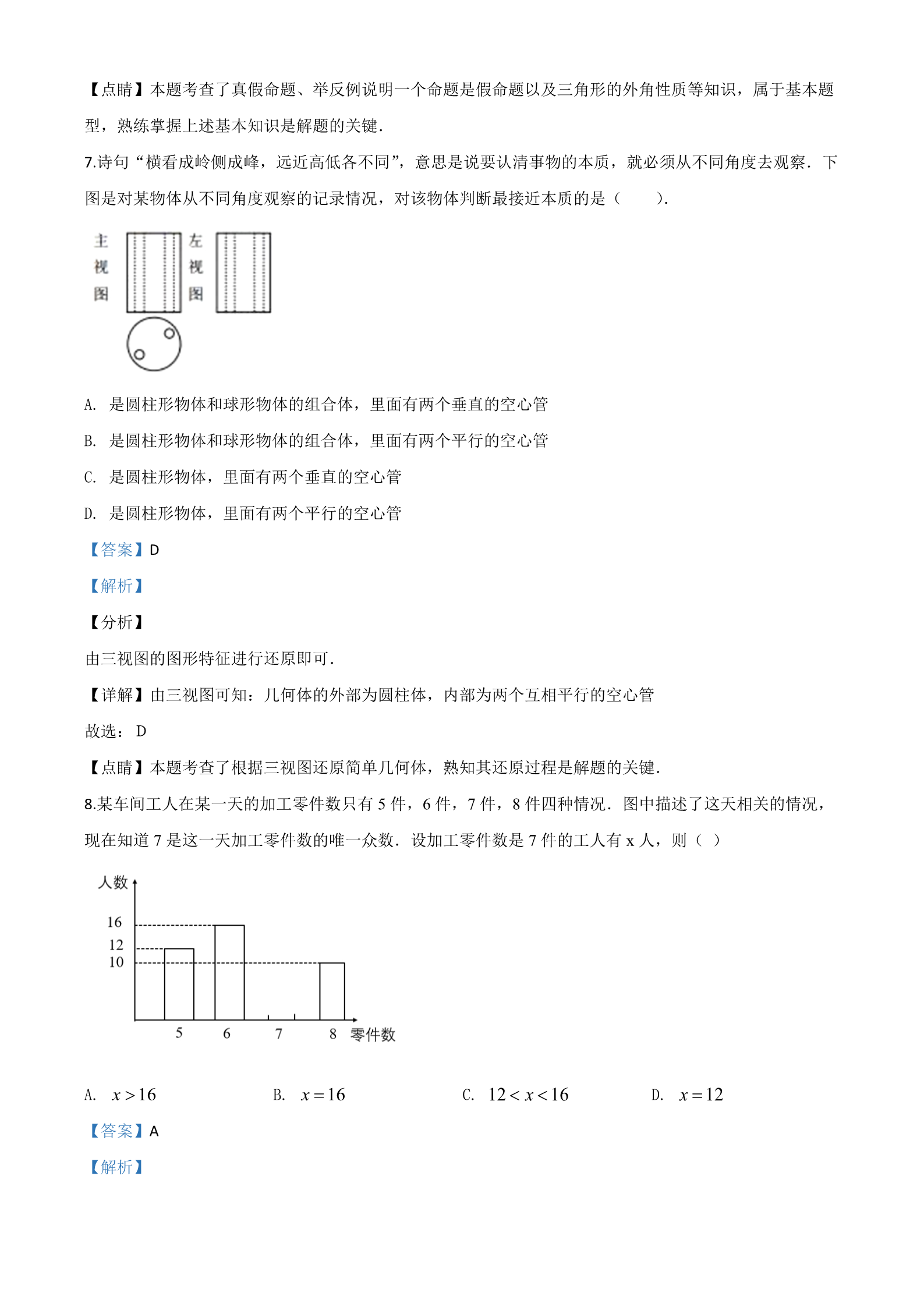
湖北省宜昌市 2020 年中考数学试题一、选择题（下列各小题中，只有一个选项是符合题目要求的，请在答题卡上指定的位置填涂符合要求的选项前面的字母代号．每小题 3 分，计 33 分．） 1. 下面四幅图是摄影爱好者抢拍的一组照片，从对称美的角度看，拍得最成功的是（）． A. B. C. D. B【答案】【解析】【分析】根据轴对称图形的特点进行判断即可．【详解】A，C，D 三幅图都不是轴对称图形，只有 B 是轴对称图形，故选：B 【点睛】本题考查了轴对称图形的性质，熟知此知识点是解题的关键． 6 吨．用科学记数 2. 我国渤海、黄海、东海、南海海水含有不少化学元素，其中铝、锰元素总量均约为 810 法表示铝、锰元素总量的和，接近值是（）． 16106 8106 1.6107 161012 A. B. C. D. C【答案】【解析】【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1 时，n 是非负数；当原数的绝对值＜1 时，n 是非正数．在这里，要先求出铝、锰元素总量的和，再科学记数法表示即可． 6【详解】解： 810 2 6=1610 7=．1.610 故选：C．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值． 3. 对于无理数，添加关联的数或者运算符号组成新的式子，其运算结果能成为有理数的是（）． 33A. B. C. D. 32 33 2 3  3 0 3 D【答案】【解析】【分析】分别计算出各选项的结果再进行判断即可．【详解】A． B．不能再计算了，是无理数，不符合题意； 2 33 2 ，是无理数，不符合题意；，是无理数，不符合题意； 3  3  2 3 3C． D． 3 =33 ，是有理数，正确． 0 3  0 故选：D．【点睛】此题主要考查了二次根式的运算，辨别运算结果，区分运算结果是否是有理数是解题的关键． 4. 如图，点 E，F，G，Q，H 在一条直线上，且，我们知道按如图所作的直线为线段FG 的垂 EF  GH l直平分线．下列说法正确的是（）． EQ A. 是线段 l的垂直平分线的垂直平分线 B. 是线段 l的垂直平分线 EH FH C. 是线段 lD. 是的垂直平分线 lEH A【答案】【解析】【分析】根据垂直平分线的定义判断即可．【详解】 ∵ 为线段FG 的垂直平分线, l∴FO=GO, 又∵EF=GH, ∴EO=HO, ∴ 是线段 l的垂直平分线,故 A正确 EH 由上可知 EO≠QO,FO≠OH,故 B、C 错误 ∵ 是直线并无垂直平分线，故D 错误 l故选：A．【点睛】本题考查垂直平分线的定义,关键在于牢记基础知识． 5. 小李、小王、小张、小谢原有位置如图（横为排、竖为列），小李在第 2 排第 4 列，小王在第 3 排第 3 列，小张在第 4 排第 2 列，小谢在第 5 排第 4 列．撤走第一排，仍按照原有确定位置的方法确定新的位置，下列说法正确的是（）． A. 小李现在位置为第 1 排第 2 列 C. 小王现在位置为第 2 排第 2 列 B. 小张现在位置为第 3 排第 2 列 D. 小谢现在位置为第 4 排第 2 列 B【答案】【解析】【分析】由于撤走一排，则四人所在的列数不变、排数减一，据此逐项排除即可．【详解】解：A. 小李现在位置第1 排第 4 列，故 A 选项错误；为B. 小张现在位置为第 3 排第 2 列，故 B 选项正确； C. 小王现在位置为第 2 排第 3 列，故 C 选项错误； D. 小谢现在位置为第 4 排第 4 列，故 D 选项错误．故选：B．【点睛】本题考查了位置的确定，根据题目信息、明确行和列的实际意义是解答本题的关键． 6. 能说明“锐角，锐角的和是锐角”是假命题的例证图是（）． A. B. C. D. C【答案】【解析】【分析】先将每个图形补充成三角形，再利用三角形的外角性质逐项判断即得答案． ，所以此图说明“锐角，锐角的和是锐角”是真命    【详解】解：A、如图 1，∠1 是锐角，且∠1= 题，故本选项不符合题意； ，所以此图说明“锐角，锐角的和是锐角”是真命题，故本选项    B、如图 2，∠2 是锐角，且∠2= 不符合题意； ，所以此图说明“锐角，锐角的和是锐角”是假命题，故本选项       C、如图 3，∠3 是钝角，且∠3= 符合题意； ，所以此图说明“锐角，锐角的和是锐角”是真命题，故本选项 D、如图 4，∠4 是锐角，且∠4= 不符合题意．故选：C．【点睛】本题考查了真假命题、举反例说明一个命题是假命题以及三角形的外角性质等知识，属于基本题型，熟练掌握上述基本知识是解题的关键． 7. 诗句“横看成岭侧成峰，远近高低各不同”，意思是说要认清事物的本质，就必须从不同角度去观察．下图是对某物体从不同角度观察的记录情况，对该物体判断最接近本质的是（）． A. 是圆柱形物体和球形物体的组合体，里面有两个垂直的空心管 B. 是圆柱形物体和球形物体的组合体，里面有两个平行的空心管 C. 是圆柱形物体，里面有两个垂直的空心管 D. 是圆柱形物体，里面有两个平行的空心管 D【答案】【解析】【分析】由三视图的图形特征进行还原即可．【详解】由三视图可知：几何体的外部为圆柱体，内部为两个互相平行的空心管故选：Ｄ【点睛】本题考查了根据三视图还原简单几何体，熟知其还原过程是解题的关键． 8. 某车间工人在某一天的加工零件数只有 5 件，6 件，7 件，8 件四种情况．图中描述了这天相关的情况，现在知道 7 是这一天加工零件数的唯一众数．设加工零件数是 7 件的工人有 x 人，则（） A. x 16 B. x 16 C. D. 12  x 16 x 12 A【答案】【解析】【分析】的根据众数定义直接判断即可．【详解】解：∵加工零件数是 5 件的工人有 12 人，加工零件数是 6 件的工人有 16 人，加工零件数是 8 件的工人有 10 人，且这一天加工零件数的唯一众数是 7， ∴加工零件数是 7 件的人数 x 16 故选：A．．【点睛】本题考查众数的意义，读懂统计图、熟练掌握众数的定义是解题的关键． 9. 游戏中有数学智慧，找起点游戏规定：从起点走五段相等直路之后回到起点，要求每走完一段直路后向右边偏行．成功的招数不止一招，可助我们成功的一招是（）． A. 每走完一段直路后沿向右偏 72°方向行走 C. 每走完一段直路后沿向右偏 108°方向行走 B. 每段直路要短 D. 每段直路要长 A【答案】【解析】【分析】根据题意可知封闭的图形是正五边形，求出正五边形内角的度数即可解决问题．【详解】根据题意可知，从起点走五段相等直路之后回到起点的封闭图形是正五边形， (5  2)180  108 ∵正五边形的每个内角的度数为： 5∴它的邻补角的度数为：180°-108°=72°，因此，每走完一段直路后沿向右偏 72°方向行走，故选：A．【点睛】此题主要考查了求正多边形内角的度数，掌握并能运用多边形内角和公式是解题的关键． 10. 如图，E，F，G 为圆上的三点，，P 点可能是圆心的是（）． FEO  50 A. B. C. D. C【答案】【解析】【分析】根据圆心角与圆周角的角度关系判断即可．【详解】同弧的圆心角是圆周角的两倍,因此 C 满足该条件．故选 C．【点睛】本题考查圆周角定理,关键在于牢记基础知识． UR11. 已知电压 U、电流 I、电阻 R 三者之间的关系式为： I  （或者），实际生活中，由于给定已 U  IR 知量不同，因此会有不同的可能图象，图象不可能是（）A. C. B. D. A【答案】【解析】【分析】在实际生活中，电压 U、电流 I、电阻 R 三者之中任何一个不能为负，依此可得结果． UI  【详解】A 图象反映的是，但自变量 R 的取值为负值，故选项 A 错误；B、C、D 选项正确，不符合 R题意．故选：A．【点睛】此题主要考查了现实生活中函数图象的确立，注意自变量取值不能为负是解答此题的关键．二、填空题（将答案写在答题卡上指定的位置．每小题 3 分，计 12 分） 1.5kg 12. 向指定方向变化用正数表示，向指定方向的相反方向变化用负数表示，“体重减少 ”换一种说法 kg 可以叙述为“体重增加_______ ”．【答案】-1.5 【解析】【分析】根据负数在生活中的应用来表示．【详解】减少 1.5kg 可以表示为增加﹣1.5kg, 故答案为:﹣1.5．【点睛】本题考查负数在生活中的应用,关键在于理解题意． 22数学讲究记忆方法．如计算 a5 时若忘记了法则，可以借助 a5  a5 a5  a55  a10 ，得到正确答 13.   5案．你计算 a2  a3 a7 结果是__________．的【答案】0 【解析】【分析】根据幂的乘方运算法则和同底数幂的乘法运算法则进行计算即可得到结果． 5【详解】 a2  a3 a7 ==a25  a37 10 10 a  a =0．故答案为：0．【点睛】此题主要考查了幂的乘方运算和同底数幂的乘法，熟练掌握运算法则是解答此题的关键． 14. 技术变革带来产品质量的提升．某企业技术变革后，抽检某一产品 2020 件，欣喜发现产品合格的频率已达到 0.9911，依此我们可以估计该产品合格的概率为_______．（结果要求保留两位小数）【答案】0.99 【解析】【分析】根据产品合格的频率已达到 0.9911，保留两位小数，所以估计合格件数的概率为 0.9９．【详解】解：合格频率为：0.9911，保留两位小数为 0.99，则根据产品合频率，估计该产品合格的概率为 0.99．故答案为 0.99．【点睛】本题考查了利用频率估计概率．用到的知识点为：概率=所求情况数与总情况数之比及运用样本数据去估计总体数据的基本解题思想． 15. 如图，在一个池塘两旁有一条笔直小路（B，C 为小路端点）和一棵小树（A 为小树位置）测得的相关数 ABC  60,ACB  60, BC  48 据为：米，则 AC  ________米．【答案】48 【解析】【分析】先说明△ABC 是等边三角形，然后根据等边三角形的性质即可解答． ABC  60,ACB  60 【详解】解：∵ ∴∠BAC=180°-60°-60°=60° ∴∠BAC=∠ABC=∠BCA=60° ∴△ABC 是等边三角形 ∴AC=BC=48 米．故答案为 48．【点睛】本题考查了等边三角形的判定和性质，证得△ABC 是等边三角形是解答本题的关键．三、解答题（将解答过程写在答题卡上指定的位置，本大题共有 9 小题，计 75 分．） 1222  2 1 16. 在“-”“×”两个符号中选一个自己想要的符号，填入中的□，并计算． 【答案】-；5 或×；5 【解析】【分析】先选择符号，然后按照有理数的四则运算进行计算即可．【详解】解：（1）选择“-” 1222  2 1 1 4  2 2 4 1  5 （2）选择“×” 1222  2 1 1 4  2 2 4 1  5 【点睛】本题考查了有理数的四则运算，熟知有理数的四则运算法则是解题的关键． x2  4x  4 x 1  (x 1)0 x  2020 17. 先化简，再求值：，其中．x 1 x  2 【答案】【解析】【分析】；2021 x 1 2先把分解因式，再进行约分化简，最后把 x=2020 代入进行计算即可． x  4x  4 x2  4x  4 x 1  (x 1)0 【详解】 x 1 x  2 (x  2)2 x 1 x 1 x  2 1  x  2 1  x 1 x  2020 当时，  2020 1 ．原式  2021 【点睛】本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值，在化简过程中要注意运算顺序和分式的化简，注意运算的结果要化成最简分式或整式． 18. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射，如图，水面与水杯下 AB 沿平行，光线从水中射向空气时发生折射，光线变成，点 G 在射线 EF 上，已知 CD EF FH HFB  20,FED  45 ，求的度数． GFH 【答案】25° 【解析】【分析】使用平行线的性质得到，再根据得到结果． GFB  FED  45 GFH  GFB  HFB 【详解】解：∵ ∴AB//CD GFB  FED  45 HFB  20 ∵∴GFH  GFB  HFB  45  20  25 【点睛】本题考查了平行线的性质，及角度间的加减计算，熟知平行线的性质是解题的关键． 19. 红光中学学生乘汽车从学校去研学旅行基地，以 75 千米/小时的平均速度，用时 2 小时到达，由于天气 t原因，原路返回时汽车平均速度控制在不低于 50 千米/小时且不高于 60 千米/小时的范围内，这样需要用 t小时到达，求的取值范围．【答案】 2.5  t  3 【解析】【分析】根据平均速度可以算出总路程，往返路程不变，再根据时间=路程÷速度的等量关系列出不等式，即可作答．【详解】解：（千米） 752  150 （小时） 150  60  2.5 （小时） 150  50  3 ∴t 的取值范围 2.5  t  3 【点睛】本题主要考查了不等式的实际应用，根据时间=路程÷速度的公式列出不等式，其中明确往返路程不变是解题的关键． 20. 宜昌景色宜人，其中三峡大坝、清江画廊、三峡人家景点的景色更是美不胜收．某民营单位为兼顾生产和业余生活，决定在下设的 A，B，C 三部门利用转盘游戏确定参观的景点，两转盘各部分圆心角大小以及选派部门、旅游景点等信息如图．（1）若规定老同志相对偏多的部门选中的可能性大，试判断这个部门是哪个部门？请说明理由；（2）设选中 C 部门游三峡大坝的概率为 P B部门游清江画廊或者三峡人家的概率为 P 1 ，选中 2 ，请判断 P ， P2 大小关系，并说明理由． 1【答案】（1）C 部门，理由见解析；（2）P1=P2，理由见解析【解析】【分析】（1）利用圆心角为 360°，A,B,C 分别占 90°，90°和 180°，分别求出所占百分比即可; （2）列出所有可能的情况，然后得出 C，B 所占比例，即可得出结果. 【详解】解：（1）C 部门， P  0.25, P  0.25, P  0.5 理由：∵ ABCP  P  P ∴CABP  P （2），12理由： C1 C2 ABC1D C1E C2D C2E 三峡大坝（D）清江画廊（E） AD BD AE BE C1F C2F 三峡人家（F） AF BF CC2 表示备注：部门转盘平均分成了 4 等份，C 部门占两份分别用，1由表可得，所有可能出现的结果共有 12 种，这些结果出现的可能性相等，其中 C 选中三峡大坝的结果有 2 种，B 选中清江画廊或者三峡人家的结果有 2 种 216P  ∴112 216P  212 P  P ∴21【点睛】本题考查了扇形图的知识．用到的知识点为：概率=所求情况数与总情况数之比．关键是分析扇形图，得到相关的数据信息． AB, BC 21. 如图，在四边形 O 中，，过点 B 的与边分别交于 ABCD AD//BC, AB  2 3a,ABC  60 OB,OE,OF ．E，F 两点．，垂足为 G，．连接 OG  BC OG  a （1）若 BF  2a ，试判断BOF 的形状，并说明理由； O （2）若，求证：与相切于点 A． AD BE  BF 【答案】（1）等腰直角三角形，理由见解析（2）见解析【解析】【分析】（1）根据题目中已知信息，可知 BF  2a ，有，所以△BOG ，都是等腰直 BG  GF  OG  a BO  OF 即可得出BOF 是等腰直角三角形；，可以等到，有，又因为 △GOF 角三角形，得到，BOF  90 （2）通过 BOE≌BOF EBO  FBO  30 BE  BF OG  BC,OG  a ，可以知道 E 与点 A 重合，再证明即可． OA  OD 【详解】解：（1）BOF 是等腰直角三角形理由如下： ∵OG  BC，BF  2a ∴BG  GF  a ∵OG  a ∴BG  GF  OG  a ∴∴∴∵∴△BOG ，都是等腰直角三角形 △GOF BOG  GOF  45 BOF  90 BO  OF BOF 是等腰直角三角形（2）证明： BE  BF，OB  OB，OE  OF ∴BOE≌BOF ∴∵∴∵EBO  FBO ABC  60 EBO  FBO  30 OG  BC,OG  a ∴∵∴BG  FG  3a BF  2 3a BE  BF  2 3a  AB ∴点 E 与点 A 重合以下有多种方法：方法一∵OA  OB ∴ABO  OAB  30 ∵AD//BC，ABC  60 ∴∴∴∵∴BAD 120 OAD  90 OA  OD O 是的半径 OA O 与相切于点 A AD 方法二∵OA  OB ，∴ ABO  OAB  30 AOB 120 ∴又∴GOB  90  OBG  60 AOB  BOG  120  60  180 ∴G，A，O 三点共线 ∵∴∴AD//BC OA  AD O 与相切于点 A． AD 方法三：如图 ∵∴AD//BC 与BC 之间距离： AD 2 3a sin60  3a 的延长线交于点 A延长 ∵交GO DA AD//BC，OG  BC ∴∵∴OA  AD OG  a OA  2a ∵∴ABO  60, AB  2 3a ，OB  2a BG  3a O 相切于点 A∴又与AD OA  2a  OA A与点重合 ∴点 AO ∴与相切于点．AD A【点睛】（1）证明三角形形状需要找到边的关系以及角的大小，通过题目中的已知信息先判断出特殊三角形，再找到所求三角形与特殊三角形边与角的关系是解题的关键；（2）本题主要考查了全等三角形的性质以及如何求切线，通过三角形全等得到角的大小，从而可以证明点 O E 与点 A 重合，再证明即可得与相切于点，其中证明点E 与点 A 重合是解题的关 AD AOA  AD 键． 22. 资料：公司营销区域面积是指公司营销活动范围内的地方面积，公共营销区域面积是指两家及以上公司营销活动重叠范围内的地方面积．材料：某地有 A，B 两家商贸公司（以下简称 A，B 公司）．去年下半年 A，B 公司营销区域面积分别为 m 2平方千米，n 平方千米，其中，公共营销区域面积与 A 公司营销区域面积的比为；今年上半年， m  3n 9受政策鼓励，各公司决策调整，A 公司营销区域面积比去年下半年增长了，B 公司营销区域面积比去年 x% 3下半年增长的百分数是 A 公司的 4 倍，公共营销区域面积与 A 公司营销区域面积的比为，同时公共营销 7区域面积与 A，B 两公司总营销区域面积的比比去年下半年增加了 x 个百分点．问题：（1）根据上述材料，针对去年下半年，提出一个你喜欢的数学问题（如求去年下半年公共营销区域面积与 B 公司营销区域面积的比），并解答；（2）若同一个公司去年下半年和今年上半年每平方千米产生的经济收益持平，且 A 公司每半年每平方千米产生的经济收益均为 B 公司的 1.5 倍，求去年下半年与今年上半年两公司总经济收益之比．【答案】（1）见解析；（2）55:72 【解析】【分析】 (1)根据题意任意写出问题解答即可. (2)根据题意列出等式，解出增长率再代入 A，B 的收益中计算即可. 【详解】解（1）问题 1：求去年下半年公共营销区域面积与 B 公司营销区域面积的比 223n   n 解答： 93223n : n  3问题 2：A 公司营销区域面积比 B 公司营销区域的面积多多少？解答： 3n  n  2n 问题 3：求去年下半年公共营销区域面积与两个公司总营销区域面积的比 223n   n 解答： 9322315n  3n  n  n  3（2）方法一： 332233n(1 x%)  3n(1 x%)  n(1 4x%)  3n(1 x%) 3n 3n  n  n  x% 779方法二： 373223  3n 1 x6 %  3n(1 x%)  n(1 4x%)  3n(1 x%)  3m  3n  n  n  x%     79方法三： m  3n 33223  m(1 x%)  m 1 x%  n(1 4x%)  xm(1 x%)  3n 3n  n  n  x%     779100(x%)2  45x% 13  0 解得 x%  20% ，x%  65% （舍去）设 B 公司每半年每平方千米产生的经济收益为 a，则 A 公司每半年每平方千米产生的经济收益为 1.5a 1.5a 3n (1 20%)  an (1 420%)  7.2na 今年上半年 A，B 公司产生的总经济收益为去年下半年 A，B 公司产生的总经济收益为 1.5a 3n  a n  5.5na (5.5na) : (7.2na)  55: 72 去年下半年与今年上半年两公司总经济收益之比为【点睛】本题考查一元二次方程增长率的问题,关键在于理解题意列出等式方程. AC, BD OD 23. 菱形的对角线相交于点 O，，点 G 是射线上一个动点，过点 G ABCD 0  ABO  60 OE,OG 作交射线于点 E，以为邻边作矩形．GE//DC OC EOGF （1）如图 1，当点 F 在线段上时，求证：；DC DF  FC （2）若延长与边交于点 H，将沿直线翻折 180°得到．GF GDH AD AD MDH ①如图 2，当点 M 在上时，求证：四边形为正方形： EG EOGF m②如图 3，当 tan ABO 为定值时，设，k 为大于 0 的常数，当且仅当时，点 M 在 DG  k  DO k  2 矩形的外部，求 m 的值． EOGF 3【答案】（1）见解析；（2）①见解析；② ．3【解析】【分析】（1）证明四边形 ECFG，DGEF 是平行四边形即可得到结论； DH  EG （2）①由折叠得可证明，，再证明可得 GDH ≌MDH 1=GEO  45 1 2 GO=EO，再由四边形 EOGF 为矩形则可证明结论； ②由四边形 ABCD 为菱形以及折叠可得，当且仅当时，M 点在矩形 1 2  3  4  5  6 k  2 EOGF 的外部，时，M 点在矩形 EOGF 上，即点 M 在 EF 上，设，求得 k  2 OB  b ，过点 D 作于点 N，证明求得 MN  b ，在 FH  OE GH  mb DN  EF HFM ∽MND RtDMN 22中运用勾股定理列出方程 2b  3mb  b2 求解即可. 【详解】（1）证明：如图，四边形EOGF 为矩形，，，，EF  OG ，GF / /OC GF  OE EF //OD ，GE / /DC 四边形 ECFG，DGEF 是平行四边形， DF  EG ，；FC  GE ，DF  FC （2）如图，证明：由折叠得，GDH ≌MDH ，，5  6 ，DG  DM DH  EG ，1 2 四边形 ABCD 为菱形，，3  4 ，GE / /CD ，3  1 ，4  5 1 5 ，，1 5  90 ，，1 5  2  45 5＋6  90 ，点 M 在 GE 上， DM / /OE ，GEO  45 ，OG  OE 四边形 EOGF 为矩形， 矩形 EOGF 为正方形；（3）如图， 四边形 ABCD 为菱形，，1 2  6 ，GE / /CD ，4  6 ，GDH ≌MDH ，3  5 ，1 2  3  4  5  6 （m 为定值）， tan ABO  m ，GDM  2ABO 点 M 始终在固定射线 DM 上并随 k 的增大向上运动， 当且仅当时，M 点在矩形 EOGF 的外部， k  2 M 点在矩形 EOGF 上，即点 M 在 EF 上， k  2 时，设，OB  b OG  k 1 b  3b ，OA  OC  mb DG  DM  kb  2b ，，OE  m k1 b  3mb ，GH  HM  mkb  2mb ，FH  OE GH  m k1 b  mkb  mb ，过点 D 作于点 N， DN  EF ，又，HMF 18090 DMN  90 DMN MDN  90 DMN ，HMF  MDN ，F  DNM  90 ，HFM ∽MND ，FH : MN  MH : DM  mb : MN  2mb : 2b   ，，MN  b 是直角三角形，，DMN DM 2  DN2  MN2 22 2b  3mb  b2 ，13m2  ，3（负值舍去），，m   30  ABO  60 3．m  3【点睛】本题考查四边形的综合问题，涉及矩形和菱形的性质，勾股定理，锐角三角函数，解方程等知识，综合程度较高，考查学生灵活运用知识的能力． y  x  2m 1, y  (2m 1)x 1 24. 已知函数均为一次函数，m 为常数． 12A 1,0 （1）如图 1，将直线绕点 逆时针旋转 45°得到直线，直线交y 轴于点 B．若直线恰好是 AO llly  x  2m 1, y  (2m 1)x 1 中某个函数的图象，请直接写出点 B 坐标以及 m 可能的值； 12y  x  2m 1, y  (2m 1)x 1 （2）若存在实数 b，使得成立，求函数图象间 | m | (b 1) 1 b  0 12的距离； y  x  2m 1 y  (2m 1)x 1 图象交 x 轴 m >1 （3）当时，函数图象分别交 x 轴，y 轴于 C，E 两点， 156 y  y y y  x  2m 1 于 D 点，将函数 1 的图象最低点 F 向上平移个单位后刚好落在一次函数图112m 1 y  y y OD 象上，设 2 的图象，线段，线段围成的图形面积为 S，试利用初中知识，探究 S 的一个近 OE 1似取值范围．（要求：说出一种得到 S 的更精确的近似值的探究办法，写出探究过程，得出探究结果，结果的取值范围两端的数值差不超过 0.01．） 3481 3 S  【答案】（1）（0,1）；1 或 0 （2）（3） 212000 10 【解析】【分析】（1）由题意，可得点 B 坐标，进而求得直线的解析式，再分情况讨论即可解的m 值； lyy（2）由非负性解得 m 和 b 的值，进而得到两个函数解析式，设 1 与 x 轴、y 轴交于 T，P， 2 分别与 x 轴、 y 轴交于 G，H，连接 GP，TH，证得四边形 GPTH 是正方形，求出 GP即为距离；（3）先根据解析式，用 m 表示出点 C、E、D 的坐标以及 y 关于 x 的表达式为 y  y  y  2m 1 x2  4m2 x  2m 1 ，得知 y 是关于 x 的二次函数且开口向上、最低点为其顶点 122  2m2 1 2m2 F  , ,根据坐标平移规则，得到关于 m 的方程，解出 m 值，即可得知点 D 、E 2m 1 2m 1 S  S 的坐标且抛物线过 D、E 点，观察图象，即可得出 S 的大体范围，如： ODE ，较小的可为平行于 DE 且与抛物线相切时围成的图形面积．【详解】解：（1）由题意可得点 B坐标为（0,1），设直线的表达式为y=kx+1，将点 A（-1,0）代入得：k=1， l所以直线的表达式为：y=x+1, ly  x  2m 1 若直线恰好是 l的图象，则 2m-1=1,解得：m=1， 1y  (2m 1)x 1 若直线恰好是 l的图象，则 2m+1=1,解得：m=0， 2B 0,1 综上， ，m  1或者 m  0  m  b 1 1b  0 （2）如图，  m  1b 1b  0  m  0 ，，1 b  0 1b  0  m  0 m  0  y  x 1 y  x 1 ，12yy设1 与 x 轴、y 轴交于 T，P， 2 分别与 x 轴、y 轴交于 G，H，连接 GP，TH ，OG  OH  OP  OT 1 PH  GT 四边形 GPTH 正方形是，GH / /PT HGP  90 ，即 HG  GP HP  2 ；GP  2 y  x  2m 1 y  2m 1 x 1 （3），12 y  x  2m 1 分别交 x 轴，y 轴于 C，E 两点 1C 1 2m,0 E 0,2m 1 ， y  2m 1 x 1 图象交 x 轴于 D 点 21D  ,0 2m 1  y  y  y  x  2m 1  2m 1 x 1 2m 1 x2  4m2 x  2m 1   12m 1 2m 1 0 y  2m 1 x2  4m2 x  2m 1 二次函数 开口向上，它的图象最低点在顶点 2  2m2 1 2m2 , F  顶点 2m 1 2m 1 56 y  x  2m 1 抛物线顶点 F 向上平移 ,刚好在一次函数图象上 12m 1 22m2 1 56 2m2 m >1 且    2m 1 2m 1 2m 1 2m 1 m  2  y  y  y  5×2 16x  3  (x  3)(5x 1) ，，12y  x  3 y  5x 1 ，∴121y  x  3 y  5x 1 ，D  ,0 E 0,3 ，由得到 1251y  5×2 16x  3得到与 x 轴，y 轴交点是 ，3,0  ,0 0,3 ，，由51D  ,0 E 0,3 ，两点抛物线经过 5 y  y1  y 2 的图象，线段 OD，线段 OE 围成的图形是封闭图形，则 S 即为该封闭图形的面积探究办法：利用规则图形面积来估算不规则图形的面积．探究过程： ①观察大于 S 的情况． S  S 很容易发现 ODE 1D  ,0 E 0,3 ，51133SODE  3  5 10 S  ，210 （若有 S 小于其他值情况，只要合理，参照赋分．） ②观察小于 S 的情况．选取小于 S 的几个特殊值来估计更精确的 S 的近似值，取值会因人而不同，下面推荐一种方法，选取以下三种特殊位置：位置一：如图当直线 MN 与 DE 平行且与抛物线有唯一交点时，设直线 MN 与 x，y 轴分别交于 M，N 1D  ,0 E 0,3 ，5DE : y 15x  3 MN : y 15x  b 直线设直线 1 y  5×2 16x  3 5×2  x  3b  0 159 20  1 4 3b  0 b  ，159 20 MN : y 15x  直线 59 M  ,0 点300 1 5959 SOMN   3481 3481 S  ，2 20 300 12000 12000 位置二：如图当直线 DR 与抛物线有唯一交点时，直线 DR 与 y 轴交于点 R 1DR : y  kx  b D  ,0 设直线，251DR : y  kx  k 直线 5 y  5×2 16x  3 15×2  16  k x 3 k  0 512 16  k  45 3 k  0 ，k 14 514 DR : y 14x  直线 514 5R 0, 点1 14 1 77SODR    S  ，25525 25 位置三：如图当直线 EQ 与抛物线有唯一交点时，直线 EQ 与 x 轴交于点 Q EQ : y  tx  3 设直线  y  5×2 16x  3 5×2  16 t x 0 2 16 t  0 ，t 16 EQ : y 16x  3 直线 3Q  ,0 点16 1399SOEQ  3  S  ，2 16 32 32 3481 9712000 32 25 我们发现：在曲线 DE 两端位置时的三角形的面积远离 S 的值，由此估计在曲线 DE 靠近中间部分时取值越接近 S 的值 3481 3 S  探究的结论：按上述方法可得一个取值范围 12000 10 的（备注：不同探究方法会有不同的结论，因而会有不同的答案．只要来龙去脉清晰、合理，即可参照赋分，但若直接写出一个范围或者范围两端数值的差不在 0.01 之间不得分．）【点睛】本题是一道综合性很强的代数与几何相结合的压轴题，知识面广，涉及有旋转的性质、坐标平移规则、非负数的性质、一次函数的图象与性质、二次函数的图象与性质、一元二次方程、不规则图形面积的估计等知识，解答的关键是认真审题，找出相关信息，利用待定系数法、数形结合法等解题方法确定解题思路，利用相关信息进行推理、探究、发现和计算．本试卷的题干 0635