浙江省绍兴市2019年中考数学真题试题（含解析）

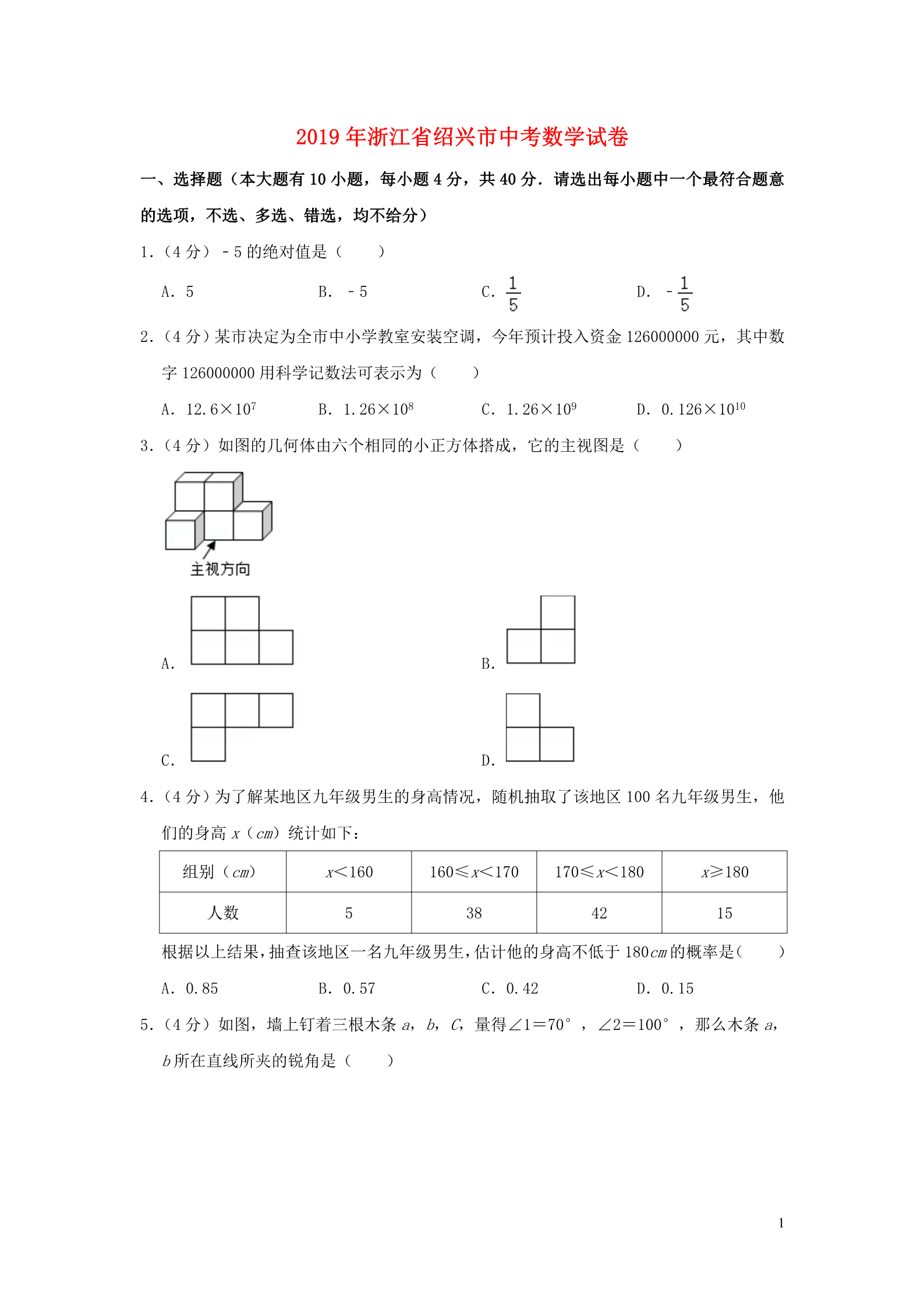
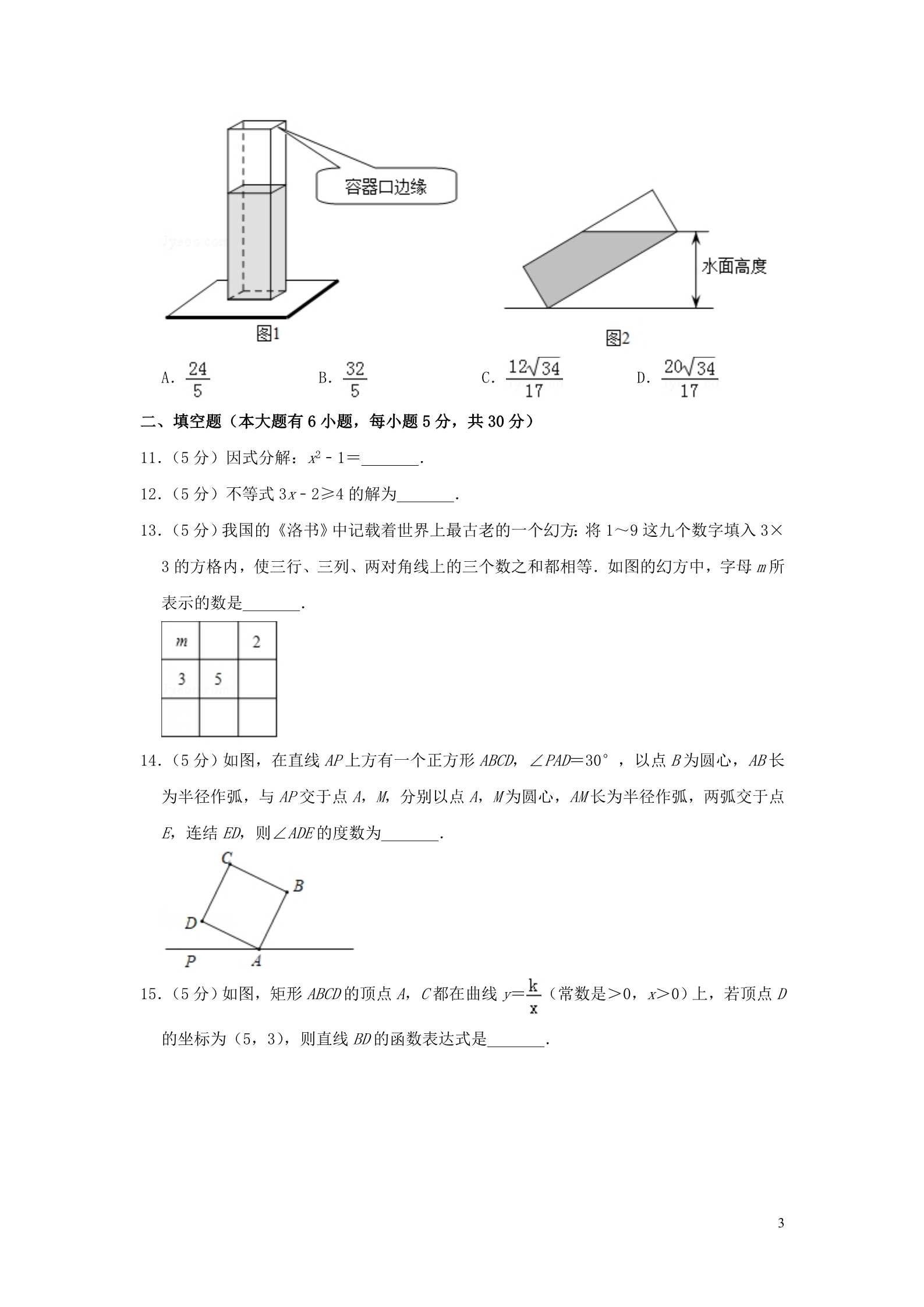
2019年浙江省绍兴市中考数学试卷一、选择题（本大题有 10小题，每小题 4分，共 40分．请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分） 1．（4分）﹣5的绝对值是（　　） A．5 B．﹣5 C． D．﹣ 2．（4分）某市决定为全市中小学教室安装空调，今年预计投入资金 126000000元，其中数字 126000000用科学记数法可表示为（　　） A．12.6×107 B．1.26×108 C．1.26×109 D．0.126×1010 3．（4分）如图的几何体由六个相同的小正方体搭成，它的主视图是（　　） A． C． B． D． 4．（4分）为了解某地区九年级男生的身高情况，随机抽取了该地区 100名九年级男生，他们的身高 x（cm）统计如下：组别（cm） x＜160 160≤x＜170 170≤x＜180 x≥180 人数 538 42 15 根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于 180cm 的概率是（　　） A．0.85 B．0.57 C．0.42 D．0.15 5．（4分）如图，墙上钉着三根木条 a，b，C，量得∠1＝70°，∠2＝100°，那么木条 a， b 所在直线所夹的锐角是（　　） 1A．5° 6．（4分）若三点（1，4），（2，7），（a，10）在同一直线上，则 a 的值等于（　　） A．﹣1 B．0 C．3 D．4 B．10° C．30° D．70° 7．（4 分）在平面直角坐标系中，抛物线 y＝（x+5）（x﹣3）经变换后得到抛物线 y＝（x+3）（x﹣5），则这个变换可以是（　　） A．向左平移 2个单位 C．向左平移 8个单位 B．向右平移 2个单位 D．向右平移 8个单位 8．（4分）如图，△ABC 内接于⊙O，∠B＝65°，∠C＝70°．若 BC＝2 ，则的长为（　　） A．π B． πC．2π D．2 π9．（4分）正方形 ABCD 的边 AB 上有一动点 E，以 EC 为边作矩形 ECFG，且边 FG 过点 D．在点 E 从点 A 移动到点 B 的过程中，矩形 ECFG 的面积（　　） A．先变大后变小 C．一直变大 B．先变小后变大 D．保持不变 10．（4分）如图 1，长、宽均为 3，高为 8的长方体容器，放置在水平桌面上，里面盛有水，水面高为 6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图 2是此时的示意图，则图 2中水面高度为（　　） 2A． B． C． D．二、填空题（本大题有 6小题，每小题 5分，共 30分） 11．（5分）因式分解：x2﹣1＝　　． 12．（5分）不等式 3x﹣2≥4的解为　　． 13．（5分）我国的《洛书》中记载着世界上最古老的一个幻方：将 1～9这九个数字填入 3× 3的方格内，使三行、三列、两对角线上的三个数之和都相等．如图的幻方中，字母 m 所表示的数是　　． 14．（5分）如图，在直线 AP 上方有一个正方形 ABCD，∠PAD＝30°，以点 B 为圆心，AB 长为半径作弧，与 AP 交于点 A，M，分别以点 A，M 为圆心，AM 长为半径作弧，两弧交于点 E，连结 ED，则∠ADE 的度数为　． 15．（5分）如图，矩形 ABCD 的顶点 A，C 都在曲线 y＝（常数是＞0，x＞0）上，若顶点 D 的坐标为（5，3），则直线 BD 的函数表达式是　． 316．（5分）把边长为 2的正方形纸片 ABCD 分割成如图的四块，其中点 O 为正方形的中心，点 E，F 分别为 AB，AD 的中点．用这四块纸片拼成与此正方形不全等的四边形 MNPQ（要求这四块纸片不重叠无缝隙），则四边形 MNPQ 的周长是　．三、解答题（本大题共 8小题，第 17～20小题每小题 8分，第 21小题 10分，第 22，23 小题每小题 8分，第 24小题 14分，共 80分．解答需写出必要的文字说明、演算步骤或证明过程） ﹣2 17．（8分）（1）计算：4sin60°+（π﹣2）0﹣（﹣ ）﹣．（2）x 为何值时，两个代数式 x2+1，4x+1的值相等？ 18．（8分）如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 y（千瓦时）关于已行驶路程 x（千米）的函数图象．（1）根据图象，直接写出蓄电池剩余电量为 35千瓦时时汽车已行驶的路程．当 0≤x≤ 150时，求 1千瓦时的电量汽车能行驶的路程．（2）当 150≤x≤200时，求 y 关于 x 的函数表达式，并计算当汽车已行驶 180千米时，蓄电池的剩余电量． 19．（8分）小明、小聪参加了 100m 跑的 5期集训，每期集训结束时进行测试，根据他们的 4集训时间、测试成绩绘制成如下两个统计图．根据图中信息，解答下列问题：（1）这 5期的集训共有多少天？小聪 5次测试的平均成绩是多少？（2）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，说说你的想法． 20．（8分）如图 1为放置在水平桌面 l 上的台灯，底座的高 AB 为 5cm，长度均为 20cm 的连杆 BC，CD 与 AB 始终在同一平面上．（1）转动连杆 BC，CD，使∠BCD 成平角，∠ABC＝150°，如图 2，求连杆端点 D 离桌面 l 的高度 DE．（2）将（1）中的连杆 CD 再绕点 C 逆时针旋转，使∠BCD＝165°，如图 3，问此时连杆端点 D 离桌面 l 的高度是增加还是减少？增加或减少了多少？（精确到 0.1cm，参考数据： ≈1.41， ≈1.73） 21．（10分）在屏幕上有如下内容：如图，△ABC 内接于⊙O，直径 AB 的长为 2，过点 C 的切线交 AB 的延长线于点 D．张老师要求添加条件后，编制一道题目，并解答． 5（1）在屏幕内容中添加条件∠D＝30°，求 AD 的长．请你解答．（2）以下是小明、小聪的对话：小明：我加的条件是 BD＝1，就可以求出 AD 的长小聪：你这样太简单了，我加的是∠A＝30°，连结 OC，就可以证明△ACB 与△DCO 全等．参考此对话，在屏幕内容中添加条件，编制一道题目（可以添线添字母），并解答． 22．（12分）有一块形状如图的五边形余料 ABCDE，AB＝AE＝6，BC＝5，∠A＝∠B＝90°，∠ C＝135°，∠E＞90°，要在这块余料中截取一块矩形材料，其中一条边在 AE 上，并使所截矩形材料的面积尽可能大．（1）若所截矩形材料的一条边是 BC 或 AE，求矩形材料的面积．（2）能否截出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由． 23．（12分）如图 1是实验室中的一种摆动装置，BC 在地面上，支架 ABC 是底边为 BC 的等腰直角三角形，摆动臂 AD 可绕点 A 旋转，摆动臂 DM 可绕点 D 旋转，AD＝30，DM＝10．（1）在旋转过程中， ①当 A，D，M 三点在同一直线上时，求 AM 的长． ②当 A，D，M 三点为同一直角三角形的顶点时，求 AM 的长．（2）若摆动臂 AD 顺时针旋转 90°，点 D 的位置由△ABC 外的点 D1转到其内的点 D2处，连结 D1D2，如图 2，此时∠AD2C＝135°，CD2＝60，求 BD2的长． 624．（14分）如图，矩形 ABCD 中，AB＝a，BC＝b，点 M，N 分别在边 AB，CD 上，点 E，F 分别在边 BC，AD 上，MN，EF 交于点 P，记 k＝MN：EF．（1）若 a：b 的值为 1，当 MN⊥EF 时，求 k 的值．（2）若 a：b 的值为，求k 的最大值和最小值．（3）若 k 的值为 3，当点 N 是矩形的顶点，∠MPE＝60°，MP＝EF＝3PE 时，求 a：b 的值． 72019年浙江省绍兴市中考数学试卷参考答案与试题解析一、选择题（本大题有 10小题，每小题 4分，共 40分．请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分） 1．（4分）﹣5的绝对值是（　　） A．5 B．﹣5 C． D．﹣ 【分析】根据绝对值的性质求解．【解答】解：根据负数的绝对值等于它的相反数，得|﹣5|＝5．故选：A．【点评】此题主要考查的是绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是 0． 2．（4分）某市决定为全市中小学教室安装空调，今年预计投入资金 126000000元，其中数字 126000000用科学记数法可表示为（　　） A．12.6×107 B．1.26×108 C．1.26×109 D．0.126×1010 【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．【解答】解：数字 126000000科学记数法可表示为 1.26×108元．故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值． 3．（4分）如图的几何体由六个相同的小正方体搭成，它的主视图是（　　） A． B． 8C． D．【分析】根据从正面看得到的视图是主视图，可得答案．【解答】解：从正面看有三列，从左起第一列有两个正方形，第二列有两个正方形，第三列有一个正方形，故 A 符合题意，故选：A．【点评】本题考查了简单组合体的三视图，从正面看得到的视图是主视图． 4．（4分）为了解某地区九年级男生的身高情况，随机抽取了该地区 100名九年级男生，他们的身高 x（cm）统计如下：组别（cm） x＜160 160≤x＜170 170≤x＜180 x≥180 人数 538 42 15 根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于 180cm 的概率是（　　） A．0.85 B．0.57 C．0.42 D．0.15 【分析】先计算出样本中身高不低于 180cm 的频率，然后根据利用频率估计概率求解．【解答】解：样本中身高不低于 180cm 的频率＝＝0.15，所以估计他的身高不低于 180cm 的概率是 0.15．故选：D．【点评】本题考查了利用频率估计概率：大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．用频率估计概率得到的是近似值，随实验次数的增多，值越来越精确． 5．（4分）如图，墙上钉着三根木条 a，b，C，量得∠1＝70°，∠2＝100°，那么木条 a， b 所在直线所夹的锐角是（　　） A．5° B．10° C．30° D．70° 【分析】根据对顶角相等求出∠3，根据三角形内角和定理计算，得到答案． 9【解答】解：∠3＝∠2＝100°， ∴木条 a，b 所在直线所夹的锐角＝180°﹣100°﹣70°＝10°，故选：B．【点评】本题考查的是三角形内角和定理、对顶角的性质，掌握三角形内角和等于 180° 是解题的关键． 6．（4分）若三点（1，4），（2，7），（a，10）在同一直线上，则 a 的值等于（　　） A．﹣1 B．0 C．3 D．4 【分析】利用（1，4），（2，7）两点求出所在的直线解析式，再将点（a，10）代入解析式即可；【解答】解：设经过（1，4），（2，7）两点的直线解析式为 y＝kx+b， ∴∴，∴y＝3x+1，将点（a，10）代入解析式，则 a＝3；故选：C．【点评】本题考查一次函数上点的特点；熟练待定系数法求函数解析式是解题的关键． 7．（4 分）在平面直角坐标系中，抛物线 y＝（x+5）（x﹣3）经变换后得到抛物线 y＝（x+3）（x﹣5），则这个变换可以是（　　） A．向左平移 2个单位 C．向左平移 8个单位 B．向右平移 2个单位 D．向右平移 8个单位【分析】根据变换前后的两抛物线的顶点坐标找变换规律．【解答】解：y＝（x+5）（x﹣3）＝（x+1）2﹣16，顶点坐标是（﹣1，﹣16）． y＝（x+3）（x﹣5）＝（x﹣1）2﹣16，顶点坐标是（1，﹣16）．所以将抛物线 y＝（x+5）（x﹣3）向右平移 2个单位长度得到抛物线 y＝（x+3）（x﹣5），故选：B．【点评】此题主要考查了次函数图象与几何变换，要求熟练掌握平移的规律：左加右减， 10 上加下减． 8．（4分）如图，△ABC 内接于⊙O，∠B＝65°，∠C＝70°．若 BC＝2 ，则的长为（　　） A．π B． πC．2π D．2 π【分析】连接 OB，OC．首先证明△OBC 是等腰直角三角形，求出 OB 即可解决问题．【解答】解：连接 OB，OC． ∵∠A＝180°﹣∠ABC﹣∠ACB＝180°﹣65°﹣70°＝45°， ∴∠BOC＝90°， ∵BC＝2 ∴OB＝OC＝2，的长为故选：A．，∴＝π，【点评】本题考查圆周角定理，弧长公式，等腰直角三角形的性质的等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 9．（4分）正方形 ABCD 的边 AB 上有一动点 E，以 EC 为边作矩形 ECFG，且边 FG 过点 D．在点 E 从点 A 移动到点 B 的过程中，矩形 ECFG 的面积（　　） 11 A．先变大后变小 C．一直变大 B．先变小后变大 D．保持不变【分析】由△BCE∽△FCD，根据相似三角形的对应边成比例，可得 CF•CE＝CD•BC，即可得矩形 ECFG 与正方形 ABCD 的面积相等．【解答】解：∵正方形 ABCD 和矩形 ECFG 中， ∠DCB＝∠FCE＝90°，∠F＝∠B＝90°， ∴∠DCF＝∠ECB， ∴△BCE∽△FCD， ∴，∴CF•CE＝CB•CD， ∴矩形 ECFG 与正方形 ABCD 的面积相等．故选：D．【点评】此题考查了正方形的性质、矩形的性质、相似三角形的判定与性质，由相似三角形得出比例线段是解题的关键． 10．（4分）如图 1，长、宽均为 3，高为 8的长方体容器，放置在水平桌面上，里面盛有水，水面高为 6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图 2是此时的示意图，则图 2中水面高度为（　　） A． B． C． D．【分析】设 DE＝x，则 AD＝8﹣x，由长方体容器内水的体积得出方程，解方程求出 DE，再由勾股定理求出 CD，过点 C 作 CF⊥BG 于 F，由△CDE∽△BCF 的比例线段求得结果即可．【解答】解：过点 C 作 CF⊥BG 于 F，如图所示： 12 设 DE＝x，则 AD＝8﹣x，根据题意得：（8﹣x+8）×3×3＝3×3×6，解得：x＝4， ∴DE＝4， ∵∠E＝90°，由勾股定理得：CD＝，∵∠BCE＝∠DCF＝90°， ∴∠DCE＝∠BCF， ∵∠DEC＝∠BFC＝90°， ∴△CDE∽△BCF， ∴即，，∴CF＝．故选：A．【点评】本题考查了勾股定理的应用、长方体的体积、梯形的面积的计算方法；熟练掌握勾股定理，由长方体容器内水的体积得出方程是解决问题的关键．二、填空题（本大题有 6小题，每小题 5分，共 30分） 11．（5分）因式分解：x2﹣1＝　（x+1）（x﹣1）　．【分析】原式利用平方差公式分解即可．【解答】解：原式＝（x+1）（x﹣1）．故答案为：（x+1）（x﹣1）．【点评】此题考查了因式分解﹣运用公式法，熟练掌握平方差公式是解本题的关键． 12．（5分）不等式 3x﹣2≥4的解为　x≥2　．【分析】先移项，再合并同类项，把 x 的系数化为 1即可．【解答】解：移项得，3x≥4+2， 13 合并同类项得，3x≥6，把 x 的系数化为 1得，x≥2．故答案为：x≥2．【点评】本题考查的是解一元一次不等式，熟知解一元一次不等式的基本步骤是解答此题的关键． 13．（5分）我国的《洛书》中记载着世界上最古老的一个幻方：将 1～9这九个数字填入 3× 3的方格内，使三行、三列、两对角线上的三个数之和都相等．如图的幻方中，字母 m 所表示的数是　4　．【分析】根据“每行、每列、每条对角线上的三个数之和相等”解答即可．【解答】解：根据“每行、每列、每条对角线上的三个数之和相等”，可知三行、三列、两对角线上的三个数之和都等于 15， ∴第一列第三个数为：15﹣2﹣5＝8， ∴m＝15﹣8﹣3＝4．故答案为：4 【点评】本题考查数的特点，抓住每行、每列、每条对角线上的三个数之和相等，数的对称性是解题的关键． 14．（5分）如图，在直线 AP 上方有一个正方形 ABCD，∠PAD＝30°，以点 B 为圆心，AB 长为半径作弧，与 AP 交于点 A，M，分别以点 A，M 为圆心，AM 长为半径作弧，两弧交于点 E，连结 ED，则∠ADE 的度数为　15°或 45°　．【分析】分点 E 与正方形 ABCD 的直线 AP 的同侧、点 E 与正方形 ABCD 的直线 AP 的两侧两种情况，根据正方形的性质、等腰三角形的性质解答．【解答】解：∵四边形 ABCD 是正方形， ∴AD＝AE，∠DAE＝90°， 14 ∴∠BAM＝180°﹣90°﹣30°＝60°，AD＝AB，当点 E 与正方形 ABCD 的直线 AP 的同侧时，由题意得，点 E 与点 B 重合， ∴∠ADE＝45°，当点 E 与正方形 ABCD 的直线 AP 的两侧时，由题意得，E′A＝E′M， ∴△AE′M 为等边三角形， ∴∠E′AM＝60°， ∴∠DAE′＝360°﹣120°﹣90°＝150°， ∵AD＝AE′， ∴∠ADE′＝15°，故答案为：15°或 45°．【点评】本题考查的是正方形的性质、等边三角形的判定和性质，掌握正方形的性质、灵活运用分情况讨论思想是解题的关键． 15．（5分）如图，矩形 ABCD 的顶点 A，C 都在曲线 y＝（常数是＞0，x＞0）上，若顶点 D 的坐标为（5，3），则直线 BD 的函数表达式是　y＝ x　．【分析】利用矩形的性质和反比例函数图象上点的坐标特征得到 A（，3），C（5，），所以 B（，），然后利用待定系数法求直线BD 的解析式．【解答】解：∵D（5，3）， 15 ∴A（，3），C（5，）， ∴B（），设直线 BD 的解析式为 y＝mx+n，，把 D（5，3），B（，）代入得，解得，∴直线 BD 的解析式为 y＝ x．故答案为 y＝ x．【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数 y＝（k 为常数，k≠ 0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值 k，即 xy＝k．也考查了矩形的性质． 16．（5分）把边长为 2的正方形纸片 ABCD 分割成如图的四块，其中点 O 为正方形的中心，点 E，F 分别为 AB，AD 的中点．用这四块纸片拼成与此正方形不全等的四边形 MNPQ（要求这四块纸片不重叠无缝隙），则四边形 MNPQ 的周长是　6+2 或 10或 8+2 　．【分析】先根据题意画出图形，再根据周长的定义即可求解．【解答】解：如图所示：图 1的周长为 1+2+3+2 ＝6+2 图 2的周长为 1+4+1+4＝10；图 3的周长为 3+5+ + ＝8+2 ；．16 故四边形 MNPQ 的周长是 6+2 或 10或 8+2 故答案为：6+2 或 10或 8+2 ．．【点评】考查了平面镶嵌（密铺），关键是得到与此正方形不全等的四边形 MNPQ（要求这四块纸片不重叠无缝隙）的各种情况．三、解答题（本大题共 8小题，第 17～20小题每小题 8分，第 21小题 10分，第 22，23 小题每小题 8分，第 24小题 14分，共 80分．解答需写出必要的文字说明、演算步骤或证明过程） ﹣2 17．（8分）（1）计算：4sin60°+（π﹣2）0﹣（﹣ ）﹣．（2）x 为何值时，两个代数式 x2+1，4x+1的值相等？【分析】（1）根据实数运算法则解答；（2）利用题意得到 x2+1＝4x+1，利用因式分解法解方程即可．【解答】解：（1）原式＝4× +1﹣4﹣2 ＝﹣3；（2）x2+1＝4x+1， x2﹣4x＝0， x（x﹣4）＝0， x1＝0，x2＝4．【点评】考查了实数的运算，因式分解法解一元二次方程．因式分解法就是先把方程的右边化为 0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为 0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）． 18．（8分）如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 y（千瓦时）关于已行驶路程 x（千米）的函数图象．（1）根据图象，直接写出蓄电池剩余电量为 35千瓦时时汽车已行驶的路程．当 0≤x≤ 150时，求 1千瓦时的电量汽车能行驶的路程．（2）当 150≤x≤200时，求 y 关于 x 的函数表达式，并计算当汽车已行驶 180千米时，蓄电池的剩余电量． 17 【分析】（1）由图象可知，蓄电池剩余电量为 35千瓦时时汽车已行驶了 150千米，据此即可求出 1千瓦时的电量汽车能行驶的路程；（2）运用待定系数法求出 y 关于 x 的函数表达式，再把 x＝180代入即可求出当汽车已行驶 180千米时，蓄电池的剩余电量．【解答】解：（1）由图象可知，蓄电池剩余电量为 35 千瓦时时汽车已行驶了 150千米． 1千瓦时的电量汽车能行驶的路程为：千米；（2）设 y＝kx+b（k≠0），把点（150，35），（200，10）代入，得∴，，∴y＝﹣0.5x+110，当 x＝180时，y＝﹣0.5×180+110＝20，答：当 150≤x≤200时，函数表达式为 y＝﹣0.5x+110，当汽车已行驶 180千米时，蓄电池的剩余电量为 20千瓦时．【点评】本题考查了一次函数的应用，解题的关键：（1）熟练运用待定系数法就解析式；（2）找出剩余油量相同时行驶的距离．本题属于基础题，难度不大，解决该类问题应结合图形，理解图形中点的坐标代表的意义． 19．（8分）小明、小聪参加了 100m 跑的 5期集训，每期集训结束时进行测试，根据他们的集训时间、测试成绩绘制成如下两个统计图． 18 根据图中信息，解答下列问题：（1）这 5期的集训共有多少天？小聪 5次测试的平均成绩是多少？（2）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，说说你的想法．【分析】（1）根据图中的信息可以求得这 5期的集训共有多少天和小聪 5次测试的平均成绩；（2）根据图中的信心和题意，说明自己的观点即可，本题答案不唯一，只要合理即可．【解答】解：（1）这 5期的集训共有：5+7+10+14+20＝56（天），小聪 5次测试的平均成绩是：（11.88+11.76+11.61+11.53+11.62）÷5＝11.68（秒），答：这 5期的集训共有 56天，小聪 5次测试的平均成绩是 11.68秒；（2）从集训时间看，集训时间不是越多越好，集训时间过长，可能造成劳累，导致成绩下滑，如图中第 4期与前面两期相比；从测试成绩看，两人的最好成绩是都是在第 4期出现，建议集训时间定为 14天．【点评】本题考查条形统计图、折线统计图、算术平均数，解答本题的关键是明确题意，利用数形结合的思想解答． 20．（8分）如图 1为放置在水平桌面 l 上的台灯，底座的高 AB 为 5cm，长度均为 20cm 的连杆 BC，CD 与 AB 始终在同一平面上．（1）转动连杆 BC，CD，使∠BCD 成平角，∠ABC＝150°，如图 2，求连杆端点 D 离桌面 l 的高度 DE．（2）将（1）中的连杆 CD 再绕点 C 逆时针旋转，使∠BCD＝165°，如图 3，问此时连杆端点 D 离桌面 l 的高度是增加还是减少？增加或减少了多少？（精确到 0.1cm，参考数据： 19 ≈1.41， ≈1.73）【分析】（1）如图 2中，作 BO⊥DE 于 O．解直角三角形求出 OD 即可解决问题．（2）作 DF⊥l 于 F，CP⊥DF 于 P，BG⊥DF 于 G，CH⊥BG 于 H．则四边形 PCHG 是矩形，求出 DF，再求出 DF﹣DE 即可解决问题．【解答】解：（1）如图 2中，作 BO⊥DE 于 O． ∵∠OEA＝∠BOE＝∠BAE＝90°， ∴四边形 ABOE 是矩形， ∴∠OBA＝90°， ∴∠DBO＝150°﹣90°＝60°， ∴OD＝BD•sin60°＝20 （cm）， ∴DF＝OD+OE＝OD+AB＝20 +5≈39.6（cm）．（2）作 DF⊥l 于 F，CP⊥DF 于 P，BG⊥DF 于 G，CH⊥BG 于 H．则四边形 PCHG 是矩形， 20 ∵∠CBH＝60°，∠CHB＝90°， ∴∠BCH＝30°， ∵∠BCD＝165°， °∠DCP＝45°， ∴CH＝BCsin60°＝10 （cm），DP＝CDsin45°＝10 （cm）， ∴DF＝DP+PG+GF＝DP+CH+AB＝（10 +10 +5）（cm）， ∴下降高度：DE﹣DF＝20 +5﹣10 ﹣10 ﹣5＝10 ﹣10 ＝3.2（cm）．【点评】本题考查解直角三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题． 21．（10分）在屏幕上有如下内容：如图，△ABC 内接于⊙O，直径 AB 的长为 2，过点 C 的切线交 AB 的延长线于点 D．张老师要求添加条件后，编制一道题目，并解答．（1）在屏幕内容中添加条件∠D＝30°，求 AD 的长．请你解答．（2）以下是小明、小聪的对话：小明：我加的条件是 BD＝1，就可以求出 AD 的长小聪：你这样太简单了，我加的是∠A＝30°，连结 OC，就可以证明△ACB 与△DCO 全等．参考此对话，在屏幕内容中添加条件，编制一道题目（可以添线添字母），并解答．【分析】（1）连接 OC，如图，利用切线的性质得∠OCD＝90°，再根据含 30度的直角三角形三边的关系得到 OD＝2，然后计算 OA+OD 即可； 21 （2）添加∠DCB＝30°，求 AC 的长，利用圆周角定理得到∠ACB＝90°，再证明∠A＝∠ DCB＝30°，然后根据含 30度的直角三角形三边的关系求 AC 的长．【解答】解：（1）连接 OC，如图， ∵CD 为切线， ∴OC⊥CD， ∴∠OCD＝90°， ∵∠D＝30°， ∴OD＝2OC＝2， ∴AD＝AO+OD＝1+2＝3；（2）添加∠DCB＝30°，求 AC 的长，解：∵AB 为直径， ∴∠ACB＝90°， ∵∠ACO+∠OCB＝90°，∠OCB+∠DCB＝90°， ∴∠ACO＝∠DCB， ∵∠ACO＝∠A， ∴∠A＝∠DCB＝30°，在 Rt△ACB 中，BC＝ AB＝1， ∴AC＝ BC＝．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理． 22．（12分）有一块形状如图的五边形余料 ABCDE，AB＝AE＝6，BC＝5，∠A＝∠B＝90°，∠ C＝135°，∠E＞90°，要在这块余料中截取一块矩形材料，其中一条边在 AE 上，并使所截矩形材料的面积尽可能大．（1）若所截矩形材料的一条边是 BC 或 AE，求矩形材料的面积．（2）能否截出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大 22 值；如果不能，说明理由．【分析】（1）①若所截矩形材料的一条边是 BC，过点 C 作 CF⊥AE 于 F，得出 S1＝AB•BC＝ 6×5＝30； ②若所截矩形材料的一条边是 AE，过点 E 作 EF∥AB 交 CD 于 F，FG⊥AB 于 G，过点 C 作 CH ⊥FG 于 H，则四边形 AEFG 为矩形，四边形 BCHG 为矩形，证出△CHF 为等腰三角形，得出 AE＝FG＝6，HG＝BC＝5，BG＝CH＝FH，求出 BG＝CH＝FH＝FG﹣HG＝1，AG＝AB﹣BG＝5，得出 S2＝AE•AG＝6×5＝30；（2）在 CD 上取点 F，过点 F 作 FM⊥AB 于 M，FN⊥AE 于 N，过点 C 作 CG⊥FM 于 G，则四边形 ANFM 为矩形，四边形 BCGM 为矩形，证出△CGF 为等腰三角形，得出 MG＝BC＝5，BM ＝CG，FG＝DG，设 AM＝x，则 BM＝6﹣x，FM＝GM+FG＝GM+CG＝BC+BM＝11﹣x，得出 S＝AM ×FM＝x（11﹣x）＝﹣x2+11x，由二次函数的性质即可得出结果．【解答】解：（1）①若所截矩形材料的一条边是 BC，如图 1所示：过点 C 作 CF⊥AE 于 F，S1＝AB•BC＝6×5＝30； ②若所截矩形材料的一条边是 AE，如图 2所示：过点 E 作 EF∥AB 交 CD 于 F，FG⊥AB 于 G，过点 C 作 CH⊥FG 于 H，则四边形 AEFG 为矩形，四边形 BCHG 为矩形， ∵∠C＝135°， ∴∠FCH＝45°， ∴△CHF 为等腰直角三角形， ∴AE＝FG＝6，HG＝BC＝5，BG＝CH＝FH， ∴BG＝CH＝FH＝FG﹣HG＝6﹣5＝1， ∴AG＝AB﹣BG＝6﹣1＝5， ∴S2＝AE•AG＝6×5＝30；（2）能；理由如下： 23 在 CD 上取点 F，过点 F 作 FM⊥AB 于 M，FN⊥AE 于 N，过点 C 作 CG⊥FM 于 G，则四边形 ANFM 为矩形，四边形 BCGM 为矩形， ∵∠C＝135°， ∴∠FCG＝45°， ∴△CGF 为等腰直角三角形， ∴MG＝BC＝5，BM＝CG，FG＝DG，设 AM＝x，则 BM＝6﹣x， ∴FM＝GM+FG＝GM+CG＝BC+BM＝11﹣x， ∴S＝AM×FM＝x（11﹣x）＝﹣x2+11x＝﹣（x﹣5.5）2+30.25， ∴当 x＝5.5时，S 的最大值为 30.25．【点评】本题考查了矩形的性质、等腰直角三角形的判定与性质、矩形面积公式以及二次函数的应用等知识；熟练掌握矩形的性质，证明三角形是等腰直角三角形是解题的关 24 键． 23．（12分）如图 1是实验室中的一种摆动装置，BC 在地面上，支架 ABC 是底边为 BC 的等腰直角三角形，摆动臂 AD 可绕点 A 旋转，摆动臂 DM 可绕点 D 旋转，AD＝30，DM＝10．（1）在旋转过程中， ①当 A，D，M 三点在同一直线上时，求 AM 的长． ②当 A，D，M 三点为同一直角三角形的顶点时，求 AM 的长．（2）若摆动臂 AD 顺时针旋转 90°，点 D 的位置由△ABC 外的点 D1转到其内的点 D2处，连结 D1D2，如图 2，此时∠AD2C＝135°，CD2＝60，求 BD2的长．【分析】（1）①分两种情形分别求解即可． ②显然∠MAD 不能为直角．当∠AMD 为直角时，根据 AM2＝AD2﹣DM2，计算即可，当∠ADM＝ 90°时，根据 AM2＝AD2+DM2，计算即可．（2）连接 CD．首先利用勾股定理求出 CD1，再利用全等三角形的性质证明 BD2＝CD1即可．【解答】解：（1）①AM＝AD+DM＝40，或 AM＝AD﹣DM＝20． ②显然∠MAD 不能为直角．当∠AMD 为直角时，AM2＝AD2﹣DM2＝302﹣102＝800， ∴AM＝20 或（﹣20 舍弃）．当∠ADM＝90°时，AM2＝AD2+DM2＝302+102＝1000， ∴AM＝10 或（﹣10 舍弃）．综上所述，满足条件的 AM 的值为 20 或 10 ．（2）如图 2中，连接 CD． 25 由题意：∠D1AD2＝90°，AD1＝AD2＝30， ∴∠AD2D1＝45°，D1D2＝30 ∵∠AD2C＝135°，，∴∠CD2D1＝90°， ∴CD1＝＝30 ，∵∠BAC＝∠A1AD2＝90°， ∴∠BAC﹣∠CAD2＝∠D2AD1﹣∠CAD2， ∴∠BAD1＝∠CAD2， ∵AB＝AC，AD2＝AD1， ∴△BAD2≌△CAD1（SAS）， ∴BD2＝CD1＝30 ．【点评】本题属于四边形综合题，考查了等腰直角三角形的性质，勾股定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型． 24．（14分）如图，矩形 ABCD 中，AB＝a，BC＝b，点 M，N 分别在边 AB，CD 上，点 E，F 分别在边 BC，AD 上，MN，EF 交于点 P，记 k＝MN：EF．（1）若 a：b 的值为 1，当 MN⊥EF 时，求 k 的值．（2）若 a：b 的值为，求k 的最大值和最小值．（3）若 k 的值为 3，当点 N 是矩形的顶点，∠MPE＝60°，MP＝EF＝3PE 时，求 a：b 的值． 26 【分析】（1）作 EH⊥BC 于 H，MQ⊥CD 于 Q，设 EF 交 MN 于点 O．证明△FHE≌△MQN （ASA），即可解决问题．（2）由题意：2a≤MN≤ a，a≤EF≤ a，当 MN 的长取最大时，EF 取最短，此时 k 的值最大最大值＝，当MN 的最短时，EF 的值取最大，此时 k 的值最小，最小值为．（3）连接 FN，ME．由 k＝3，MP＝EF＝3PE，推出＝＝3，推出＝＝2，由△ PNF∽△PME，推出＝＝2，ME∥NF，设 PE＝2m，则 PF＝4m，MP＝6m，NP＝12m，接下来分两种情形①如图 2中，当点 N 与点 D 重合时，点 M 恰好与 B 重合．②如图 3中，当点 N 与 C 重合，分别求解即可．【解答】解：（1）如图 1中，作 EH⊥BC 于 H，MQ⊥CD 于 Q，设 EF 交 MN 于点 O． ∵四边形 ABCD 是正方形， ∴FH＝AB，MQ＝BC， ∵AB＝CB， ∴EH＝MQ， ∵EF⊥MN， ∴∠EON＝90°， ∵∠ECN＝90°， ∴∠MNQ+∠CEO＝180°，∠FEH+∠CEO＝180° ∴∠FEH＝∠MNQ，∵∠EHF＝∠MQN＝90°， ∴△FHE≌△MQN（ASA）， ∴MN＝EF， ∴k＝MN：EF＝1． 27 （2）∵a：b＝1：2， ∴b＝2a，由题意：2a≤MN≤ a，a≤EF≤ a， ∴当 MN 的长取最大时，EF 取最短，此时 k 的值最大最大值＝，当 MN 的最短时，EF 的值取最大，此时 k 的值最小，最小值为．（3）连接 FN，ME． ∵k＝3，MP＝EF＝3PE， ∴∴＝＝＝3，＝2，∵∠FPN＝∠EPM， ∴△PNF∽△PME，＝2，ME∥NF，设 PE＝2m，则 PF＝4m，MP＝6m，NP＝12m， ∴＝①如图 2中，当点 N 与点 D 重合时，点 M 恰好与 B 重合．作 FH⊥BD 于 H． ∵∠MPE＝∠FPH＝60°， ∴PH＝2m，FH＝2 m，DH＝10m， ∴＝＝＝．②如图 3中，当点 N 与 C 重合，作 EH⊥MN 于 H．则 PH＝m，HE＝ m， ∴HC＝PH+PC＝13m， 28 ∴tan∠HCE＝ ∵ME∥FC，＝＝，∴∠MEB＝∠FCB＝∠CFD， ∵∠B＝∠D， ∴△MEB∽△CFD， ∴∴＝＝2，＝＝＝，综上所述，a：b 的值为或．【点评】本题属于相似形综合题，考查了正方形的性质，全等三角形的判定和性质，矩形的性质，相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会用分类讨论的思想思考问题，属于中考压轴题． 29