浙江省宁波市2019年中考数学真题试题

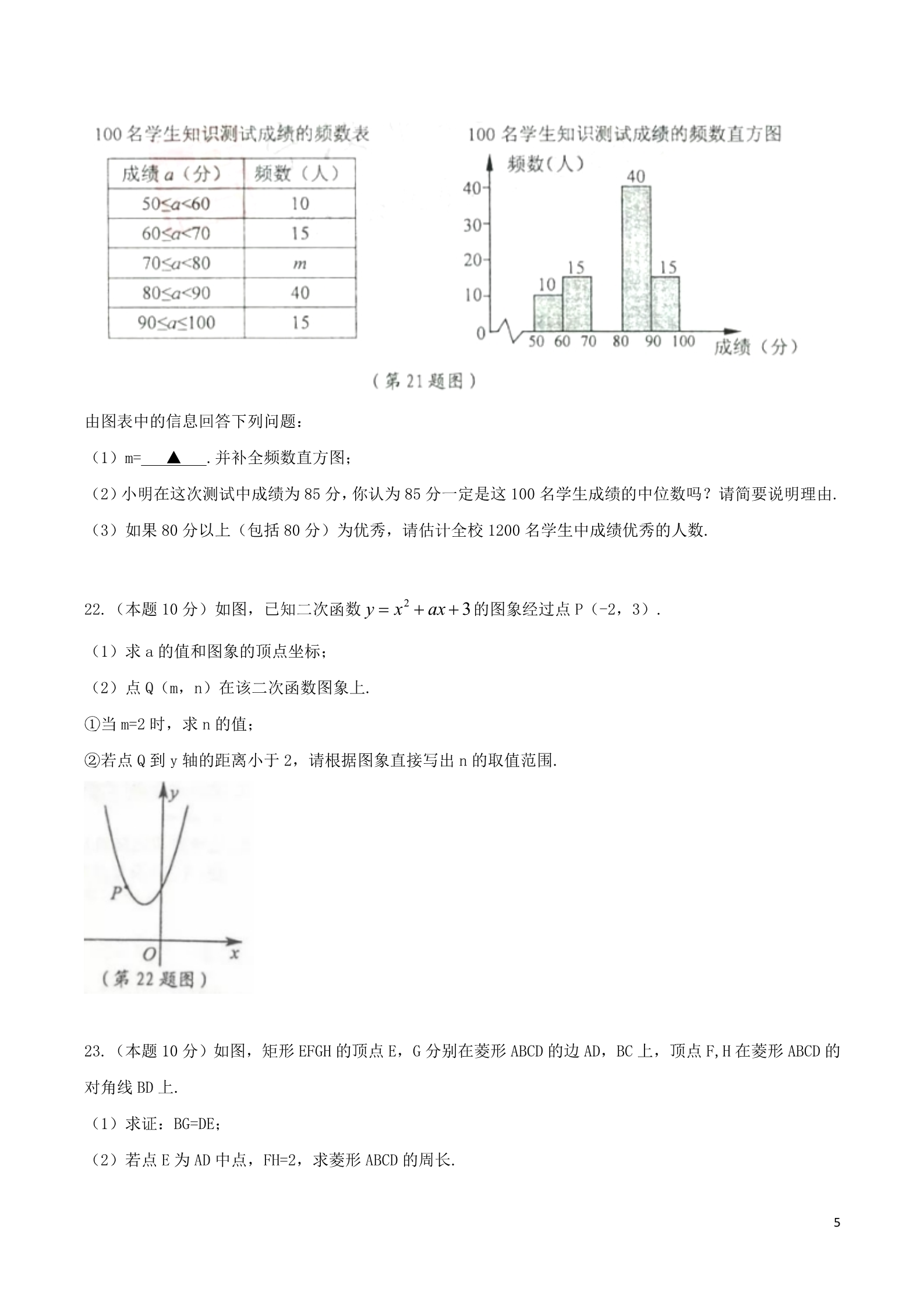
宁波市 2019年初中学业水平考试数学试题姓名：准考证号：考试须知：试题卷 I 一、选择题（每小题 4分，共 48分，在每小题给出的四个选项中，只有一个符合题目要求） 1. -2的绝对值为 1212A. B.2 C. D. -2 2.下列计算正确的是 A.a3  a2  a5 B.a3 a2  a6 C.(a2 )3  a5 D.a6  a2  a4 3.宁波是世界银行在亚洲地区选择的第一个展开垃圾分类试点项目的城市，项目总投资为 1 526 000 000元人民币，数 1 526 000 000用科学计数法表示为 A. 1.526×108 B.15.26×108 C.1.526×109 D.1.526×1010 14.若分式有意义，则 x的取值范围是 x  2 A.x  2 5.如图，下列关于物体的主视图画法正确的是 B. x  2 C.x  0 D.x  2 3 x 26.不等式  x 的解为 B.x  1 A.x 1 C.x 1 D.x  1 17.能说明命题“关于 x的方程 x2  4x  m  0一定有实数根”是假命题的反例为 A.m=-1 B.m=0 C.m=4 D.m=5 8.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了 10棵，每棵产量的平均数克）及方差 S2 （单位：千克 2）如下表所示： x （单位：千今年准备从四个品种选出一种产量既高又稳定的葡萄树进行种植，应选的品种是 A.甲 B.乙 C.丙 D.丁 9.已知直线 m∥n，将一块含 45°的直角三角板 ABC按如图方式放置，其中斜边 BC与直线 n交于点 D，若∠ 1=25°，则∠2的度数为 A.60° B.65° C.70° D.75° 10.如图所示，矩形 ABCD中，AD=6cm，把它分割成正方形纸片 ABEF和矩形纸片 EFCD后，分别裁出扇形 ABF 和半径最大的圆，恰好能做一个圆锥的侧面和底面，则 AB的长为 A. 3.5cm B. 4cmC. 4.5cm D. 5cm 11.小慧去花店购买鲜花，若买 5支玫瑰和 3支百合，则她所带的钱剩下 10元，若购买 3支玫瑰和 5支百合，则她所带的钱还缺 4元，若只购买 8玫瑰，则她所带的钱剩下 A.31元 B.30元 C.25元 D.19元 12.勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载.如图 1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图 2的方式放置在最大的正方形内，若知道图中阴影的面积，则一定能求出 A.直角三角形的面积 B.最大正方形的面积 C.较小两个正方形重叠部分的面积 D.最大正方形和直角三角形的面积和 2试题卷 II 二、填空题（每小题 4分，共 24分） 13.请写出一个小于 4的无理数： 14.分解因式： x2  xy  15.袋中装有除颜色外其余均相同的 5个红球和 3个白球，从袋中任意摸出一个球，则摸出的球是红球的概率为 16.如图，某海防哨所 O发现在它的西北方向，距离哨所 400米的 A处有一艘船向正东方向航行，航行一段时间后到达哨所北偏东 60°方向的 B处，则此时这艘船与哨所的距离 OB约为米.（精确到 1米， ▲.▲.▲.▲参考数据： 2 1.414, 31.732 ）17.如图，Rt△ABC中，∠C=90°，AC=12，点 D在边 BC上，CD=5，BD=13.点 P是线段 AD上一动点，当半径为 6的圆 P与△ABC的一边相切时，AP的长为 ▲.k18.如图，过原点的直线与反比例函数 y  (k  0) 的图象交于 A、B两点，点 A在第一象限，点 C在 x轴 x正半轴上，连接 AC交反比例函数图象于点 D，AE是∠BAC的平分线，过点 B作 AE垂线，垂足为 E，连接 DE，若 AC=3CD，△ADE的面积为 8，则 k的值为 ▲.3三、解答题（本大题有 8小题，共 78分） 19.（本题 6分）先化简，在求值： (x  2)(x  2)  x(x 1)，其中 x  3 .20.（本题 8分）图 1，图 2都是由边长为 1的小等边三角形构成的网格，每个网格图中有 5个小等边三角形已涂上阴影，请在余下的空白小等边三角形中，按下列要求选取一个涂上阴影：（1）使得 6个阴影小等边三角形组成一个轴对称图形；（2）使得 6个阴影小等边三角形组成一个中心对称图形. （请将两个小题依次作答在图 1，图 2中，均需要画出符合条件的一种情形） 21.（本题 8分）今年 5月 15日，亚洲文明对话大会在北京开幕.为了增进学生对亚洲文化的了解，某学校开展了相关知识的宣传教育活动，为了了解这次活动的效果，学校从全校 1200名学生中随机抽取 100名学生进行知识测试（测试成绩满分 100分，得分均为整数），并根据这 100人的测试成绩，制作了如下的统计表： 4由图表中的信息回答下列问题：（1）m= ▲ .并补全频数直方图；（2）小明在这次测试中成绩为 85分，你认为 85分一定是这 100名学生成绩的中位数吗？请简要说明理由. （3）如果 80分以上（包括 80分）为优秀，请估计全校 1200名学生中成绩优秀的人数. 22.（本题 10分）如图，已知二次函数 y  x2  ax  3的图象经过点 P（-2，3）. （1）求 a的值和图象的顶点坐标；（2）点 Q（m，n）在该二次函数图象上. ①当 m=2时，求 n的值； ②若点 Q到 y轴的距离小于 2，请根据图象直接写出 n的取值范围. 23.（本题 10分）如图，矩形 EFGH的顶点 E，G分别在菱形 ABCD的边 AD，BC上，顶点 F,H在菱形 ABCD的对角线 BD上. （1）求证：BG=DE；（2）若点 E为 AD中点，FH=2，求菱形 ABCD的周长. 524.（本题 10分）某景区内的公路如图 1所示，景区内有免费的班车，从入口处出发，沿该公路开往草甸，途中停靠塔林（上下车时间忽略不计），第一班车上午 8点出发，以后每隔 10分钟有一班车从入口处发车，小聪周末到该景区游玩，上午 7:40到达入口，因还没到发车时间，于是从景区入口处出发，沿该公路步行 25分钟后到达塔林，离入口的路程 y（米）与时间 x（分钟）的函数关系式如图 2所示. （1）求第一班车离入口处的路程 y（米）与时间 x（分钟）的函数表达式；（2）求第一班车从入口处到达塔林所需的时间；（3）小聪在塔林游玩 40分钟后，想坐班车到草甸，则小聪最早能够坐上第几班车？如果他做这班车到草甸，比他在塔林游玩结束后立即步行到草甸提早了几分钟？（假设每一班车速度均相同，小聪步行速度不变） 25.（本题 12分）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线. （1）如图 1，在△ABC中，AB=AC,AD是△ABC的角平分线，E,F分别是 BD,AD上的点，求证：四边形 ABEF 是邻余四边形. （2）如图 2，在 5×4的方格纸中，A,B在格点上，请画出一个符合条件的邻余四边形 ABEF，使得 AB是邻 6余线，E,F在格点上. （3）如图 3，在（1）的条件下，取 EF中点 M，连接 DM并延长交 AB于点 Q，延长 EF交 AC于点 N，若 N为 AC的中点，DE=2BE,QB=3，求邻余线 AB的长. 26.（本题 14分）如图 1，圆 O经过等边△ABC的顶点 A,C（圆心 O在△ABC内），分别与 AB,CB的延长线交于点 D,E，连接 DE,BF⊥EC交 AE于点 F. （1）求证：BD=BE；（2）当 AF:EF=3:2，AC=6时，求 AE的长； AF （3）设  x, tan DAE  y .EF ①求 y关于 x的函数表达式； ②如图 2，连接 OF，OB，若△AEC的面积是△OFB面积的 10倍，求 y的值. 78910 11 12 13 14