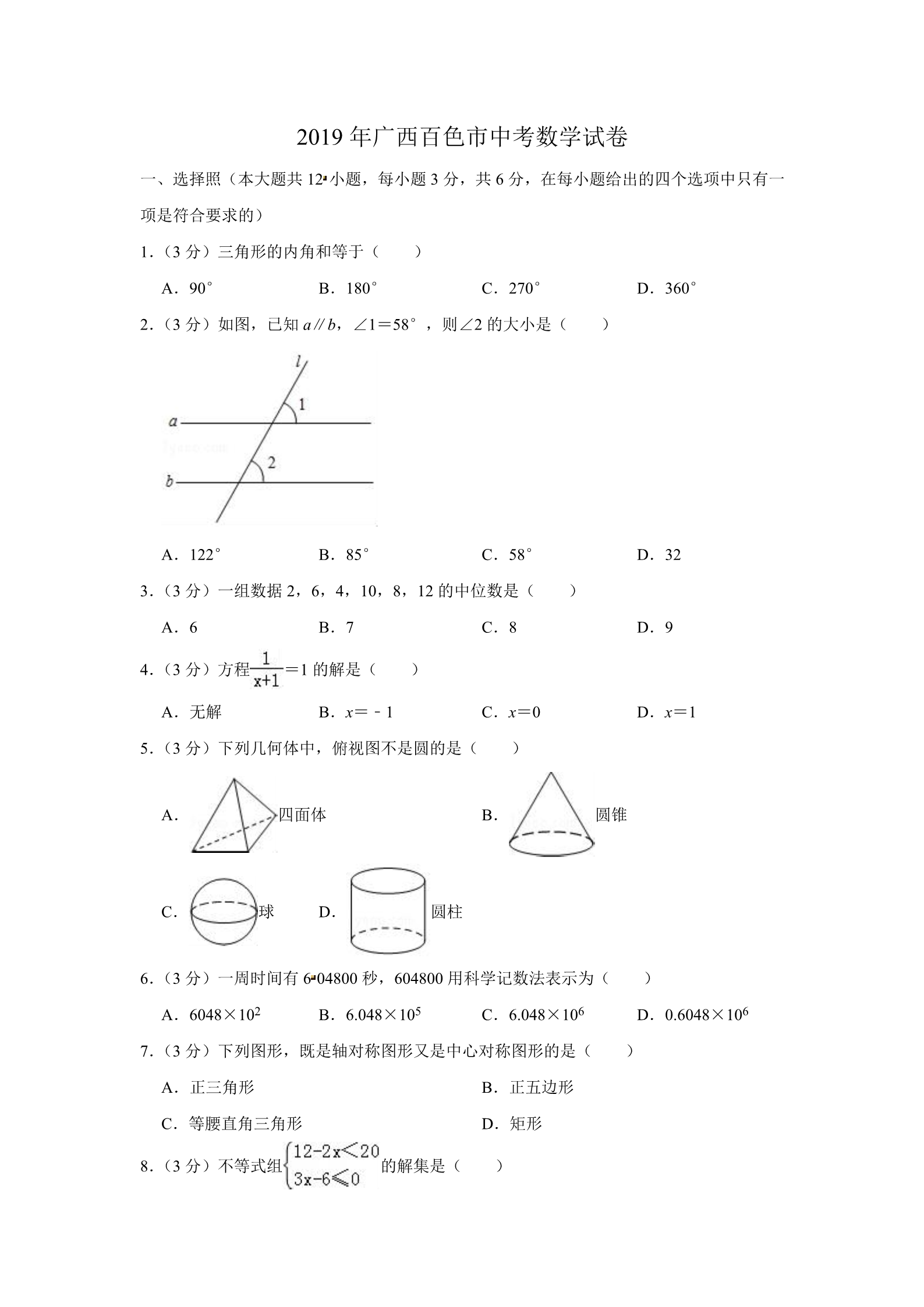
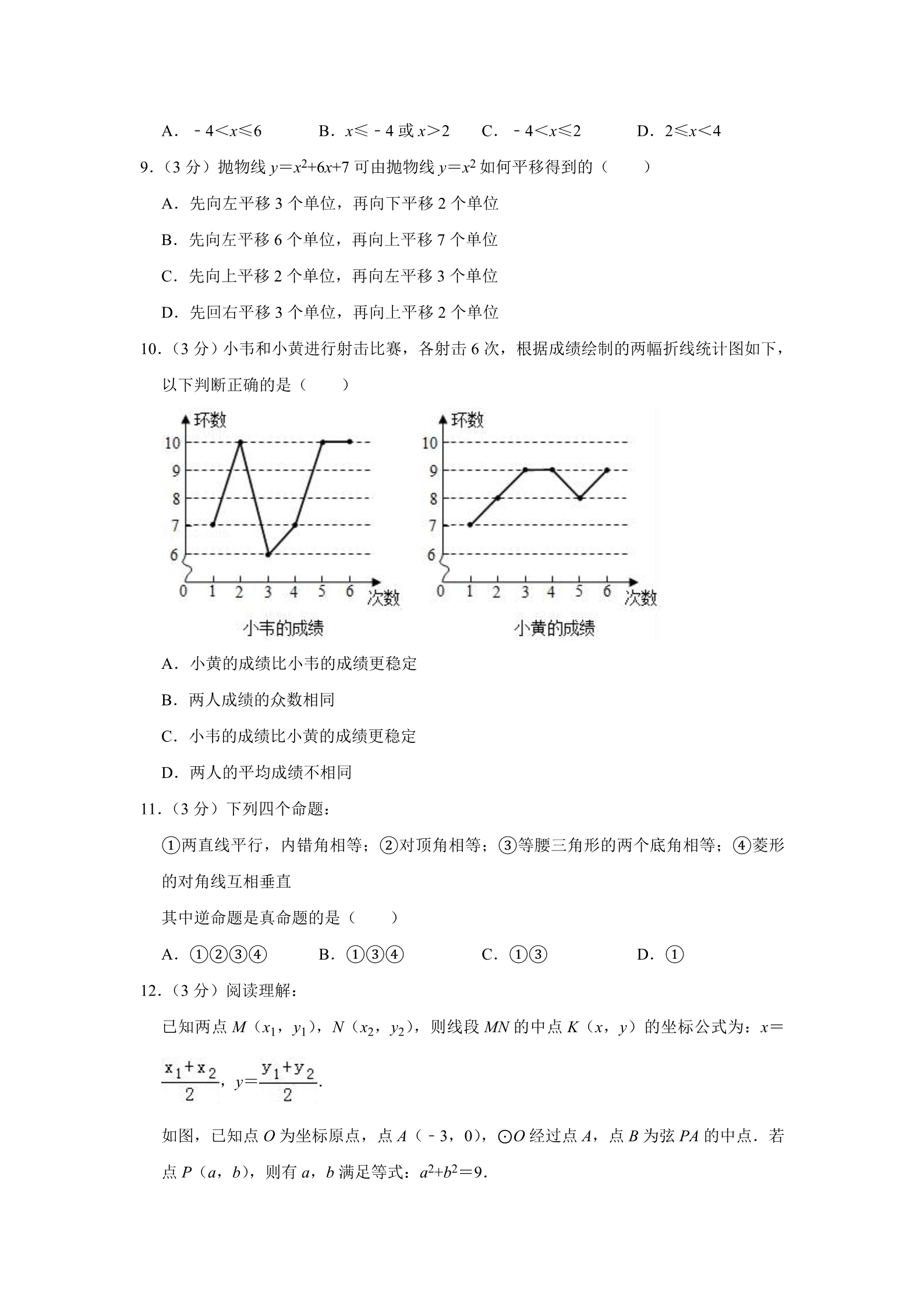
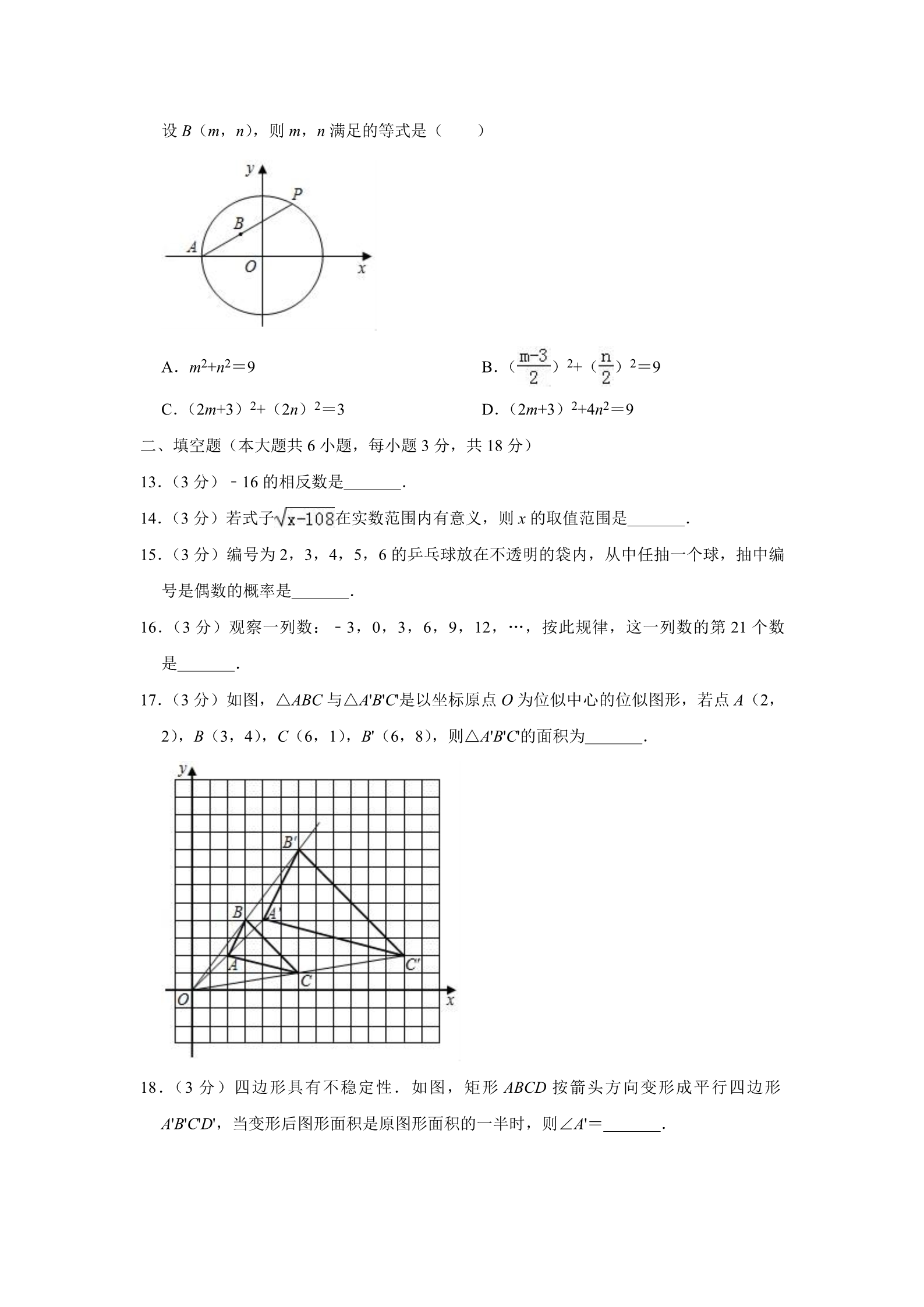
2019年广西百色市中考数学试题（Word版，含解析）下载

2019 年广西百色市中考数学试卷 一、选择照（本大题共 12 小题，每小题 3 分，共 6 分，在每小题给出的四个选项中只有一 项是符合要求的） 1．（3 分）三角形的内角和等于（　　） A．90° B．180° C．270° D．360° 2．（3 分）如图，已知 a∥b，∠1＝58°，则∠2 的大小是（　　） A．122° B．85° C．58° D．32 D．9 3．（3 分）一组数据 2，6，4，10，8，12 的中位数是（　　） A．6 B．7 C．8 4．（3 分）方程 A．无解 ＝1 的解是（　　） B．x＝﹣1 C．x＝0 D．x＝1 5．（3 分）下列几何体中，俯视图不是圆的是（　　） A． C． 四面体 B． 圆锥 球D． 圆柱 6．（3 分）一周时间有 6 04800 秒，604800 用科学记数法表示为（　　） A．6048×102 B．6.048×105 C．6.048×106 D．0.6048×106 7．（3 分）下列图形，既是轴对称图形又是中心对称图形的是（　　） A．正三角形 B．正五边形 D．矩形 C．等腰直角三角形 8．（3 分）不等式组 的解集是（　　） A．﹣4＜x≤6 B．x≤﹣4 或 x＞2 C．﹣4＜x≤2 D．2≤x＜4 9．（3 分）抛物线 y＝x2+6x+7 可由抛物线 y＝x2 如何平移得到的（　　） A．先向左平移 3 个单位，再向下平移 2 个单位 B．先向左平移 6 个单位，再向上平移 7 个单位 C．先向上平移 2 个单位，再向左平移 3 个单位 D．先回右平移 3 个单位，再向上平移 2 个单位 10．（3 分）小韦和小黄进行射击比赛，各射击 6 次，根据成绩绘制的两幅折线统计图如下， 以下判断正确的是（　　） A．小黄的成绩比小韦的成绩更稳定 B．两人成绩的众数相同 C．小韦的成绩比小黄的成绩更稳定 D．两人的平均成绩不相同 11．（3 分）下列四个命题： ①两直线平行，内错角相等；②对顶角相等；③等腰三角形的两个底角相等；④菱形 的对角线互相垂直 其中逆命题是真命题的是（　　） A．①②③④ B．①③④ C．①③ D．① 12．（3 分）阅读理解： 已知两点 M（x1，y1），N（x2，y2），则线段 MN 的中点 K（x，y）的坐标公式为：x＝ ，y＝ ．如图，已知点 O 为坐标原点，点 A（﹣3，0），⊙O 经过点 A，点 B 为弦 PA 的中点．若 点 P（a，b），则有 a，b 满足等式：a2+b2＝9． 设 B（m，n），则 m，n 满足的等式是（　　） A．m2+n2＝9 B．（ ）2+（ ）2＝9 C．（2m+3）2+（2n）2＝3 D．（2m+3）2+4n2＝9 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 13．（3 分）﹣16 的相反数是　 　． 14．（3 分）若式子 在实数范围内有意义，则 x 的取值范围是　 15．（3 分）编号为 2，3，4，5，6 的乒乓球放在不透明的袋内，从中任抽一个球，抽中编 号是偶数的概率是　． 　． 16．（3 分）观察一列数：﹣3，0，3，6，9，12，…，按此规律，这一列数的第 21 个数 是　． 17．（3 分）如图，△ABC 与△A’B’C’是以坐标原点 O 为位似中心的位似图形，若点 A（2， 2），B（3，4），C（6，1），B’（6，8），则△A’B’C’的面积为　． 18．（3 分）四边形具有不稳定性．如图，矩形 ABCD 按箭头方向变形成平行四边形 A’B’C’D’，当变形后图形面积是原图形面积的一半时，则∠A’＝　． 三、解答题（本大题共 8 小题，共 66 分，解答应写出文字说明、证明过程或演算步骤） 19．（6 分）计算：（﹣1）3+ ﹣（π﹣112）0﹣2 tan60° 20．（6 分）求式子 ÷的值，其中 m＝﹣2019． 21．（6 分）如图，已如平行四边形 OABC 中，点 O 为坐标顶点，点 A（3，0），C（1，2）， 函数 y＝ （k≠0）的图象经过点 C． （1）求 k 的值及直线 OB 的函数表达式： （2）求四边形 OABC 的周长． 22．（8 分）如图，菱形 ABCD 中，作 BE⊥AD、CF⊥AB，分别交 AD、AB 的延长线于点 E、F． （1）求证：AE＝BF； （2）若点 E 恰好是 AD 的中点，AB＝ 2，求 BD 的值． 23．（8 分）九年级（1）班全班 50 名同学组成五个不同的兴趣爱好小组，每人都参加且只 能参加一个小组，统计（不完全）人数如下表： 编号 人数 一二三四五a15 20 10 b已知前面两个小组的人数之比是 1：5． 解答下列问题： （1）a+b＝　 　． （2）补全条形统计图： （3）若从第一组和第五组中任选两名同学，求这两名同学是同一组的概率．（用树状图 或列表把所有可能都列出来） 24．（10 分）一艘轮船在相距 90 千米的甲、乙两地之间匀速航行，从甲地到乙地顺流航行 用 6 小时，逆流航行比顺流航行多用 4 小时． （1）求该轮船在静水中的速度和水流速度； （2）若在甲、乙两地之间建立丙码头，使该轮船从甲地到丙地和从乙地到丙地所用的航 行时间相同，问甲、丙两地相距多少干米？ 25．（10 分）如图，已知 AC、AD 是⊙O 的两条割线，AC 与⊙O 交于 B、C 两点，AD 过圆 心 O 且与⊙O 交于 E、D 两点，OB 平分∠AOC． （1）求证：△ACD∽△ABO； （2）过点 E 的切线交 AC 于 F，若 EF∥OC，OC＝3，求 EF 的值．[提示：（ +1）（ ﹣1）＝1] 26．（12 分）已知抛物线 y＝mx2 和直线 y＝﹣x+b 都经过点 M（﹣2，4），点 O 为坐标原点， 点 P 为抛物线上的动点，直线 y＝﹣x+b 与 x 轴、y 轴分别交于 A、B 两点． （1）求 m、b 的值； （2）当△PAM 是以 AM 为底边的等腰三 角形时，求点 P 的坐标； （3）满足（2）的条件时，求 sin∠BOP 的值． 2019 年广西百色市中考数学试卷 参考答案与试题解析 一、选择照（本大题共 12 小题，每小题 3 分，共 6 分，在每小题给出的四个选项中只有一 项是符合要求的） 1．（3 分）三角形的内角和等于（　　） A．90° B．180° C．270° D．360° 【分析】根据三角形的内角和定理进行解答便可． 【解答】解：因为三角形的内角和等于 180 度， 故选：B． 【点评】本题主要考查了三角形的内角和定理，熟记“三角形的内角和等于 180 度“是 解题的关键． 2．（3 分）如图，已知 a∥b，∠1＝58°，则∠2 的大小是（　　） A．122° B．85° C．58° D．32 【分析】根据平行线的性质进行解答便可． 【解答】解：∵a∥b， ∴∠1＝∠2， ∵∠1＝58°， ∴∠2＝58°， 故选：C． 【点评】本题主要考查了平行线的性质：两直线平行，同位角相等，是一个基础题，关 键是熟记定理． 3．（3 分）一组数据 2，6，4，10，8，12 的中位数是（　　） A．6 B．7 C．8 D．9 【分析】将数据重新排列，再根据中位数的概念求解可得． 【解答】解：将数据重新排列为 2、4、6、8、10、12， 所以这组数据的中位数为 ＝7， 故选：B． 【点评】本题主要考查中位数，解题的关键是掌握将一组数据按照从小到大（或从大到 小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位 数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数． 4．（3 分）方程 A．无解 ＝1 的解是（　　） B．x＝﹣1 C．x＝0 D．x＝1 【分析】移项可得 【解答】解： ﹣1＝ ＝1， ﹣1＝ ＝0，可得 x＝0； ∴移项可得 ＝0， ∴x＝0， 经检验 x＝0 是方程的根， ∴方程的根是 x＝0； 故选：C． 【点评】本题考查分式方程的解法；掌握分式方程的求解方法，验根是关键． 5．（3 分）下列几何体中，俯视图不是圆的是（　　） A． 四面体 B． 圆锥 C． 球D． 圆柱 【分析】分别找出从图形的上面看所得到的图形即可． 【解答】解：A、俯视图是三角形，故此选项正确； B、俯视图是圆，故此选项错误； C、俯视图是圆，故此选项错误； D、俯视图是圆，故此选项错误； 故选：A． 【点评】此题主要考查了简单几何体的三视图，关键是掌握俯视图是从几何体的上面看 所得到的图形． 6．（3 分）一周时间有 6 04800 秒，604800 用科学记数法表示为（　　） A．6048×102 B．6.048×105 C．6.048×106 D．0.6048×106 【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的 值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同．当原数绝对值＞1 时，n 是正数；当原数的绝对值＜1 时，n 是负数． 【解答】解：数字 604800 用科学记数法表示为 6.048×105． 故选：B． 【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的形式，其 中 1≤|a|＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值． 7．（3 分）下列图形，既是轴对称图形又是中心对称图形的是（　　） A．正三角形 B．正五边形 D．矩形 C．等腰直角三角形 【分析】根据轴对称图形与中心对称图形的概念求解． 【解答】解：A．正三角形是轴对称图形，不是中心对称图形； B．正五边形是轴对称图形，不是中心对称图形； C．等腰直角三角形是轴对称图形，不是中心对称图形； D．矩形是轴对称图形，也是中心对称图形； 故选：D． 【点评】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称 轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转 180 度后两部分 重合． 8．（3 分）不等式组 A．﹣4＜x≤6 的解集是（　　） B．x≤﹣4 或 x＞2 C．﹣4＜x≤2 D．2≤x＜4 【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中 间找、大大小小无解了确定不等式组的解集． 【解答】解：解不等式 12﹣2x＜20，得：x＞﹣4， 解不等式 3x﹣6≤0，得：x≤2， 则不等式组的解集为﹣4＜x≤2． 故选：C． 【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知 “同大取大；同小取小；大小小 大中间找；大大小小找不到”的原则是解答此题的关 键． 9．（3 分）抛物线 y＝x2+6x+7 可由抛物线 y＝x2 如何平移得到的（　　） A．先向左平移 3 个单位，再向下平移 2 个单位 B．先向左平移 6 个单位，再向上平移 7 个单位 C．先向上平移 2 个单位，再向左平移 3 个单位 D．先回右平移 3 个单位，再向上平移 2 个单位 【分析】按照“左加右减，上加下减”的规律求则可． 【解答】解：因为 y＝x2+6x+7＝（x+3）2﹣2． 所以将抛物线 y＝x2 先向左平移 3 个单位，再向下平移 2 个单位即可得到抛物线 y＝ x2+6x+7． 故选：A． 【点评】考查了抛物线的平移以及抛物线解析式的变化规律：左加右减，上加下减． 10．（3 分）小韦和小黄进行射击比赛，各射击 6 次，根据成绩绘制的两幅折线统计图如下， 以下判断正确的是（　　） A．小黄的成绩比小韦的成绩更稳定 B．两人成绩的众数相同 C．小韦的成绩比小黄的成绩更稳定 D．两人的平均成绩不相同 【分析】根据折线统计图得出两人成绩的波动幅度，结合众数、平均数和方差的定义逐 一判断即可得． 【解答】解：A，由折线统计图知，小黄的成绩波动幅度小，成绩更稳定，此选项正确， C 选项错误； B．小韦成绩的众数为 10 环，小黄成绩的众数为 9 环，此选项错误； D．小韦成绩的平均数为 ＝，小黄的平均成绩为 ＝，此选项错误； 故选：A． 【点评】此题考查了折线统计图，方差，平均数，弄清题意是解本题的关键． 11．（3 分）下列四个命题： ①两直线平行，内错角相等；②对顶角相等；③等腰三角形的两个底角相等；④菱形 的对角线互相垂直 其中逆命题是真命题的是（　　） A．①②③④ B．①③④ C．①③ D．① 【分析】首先写出各个命题的逆命题，然后进行判断即可． 【解答】解：①两直线平行，内错角相等；其命题：内错角相等两直线平行是真命题； ②对顶角相等，其逆命题：相等的角是对顶角是假命题； ③等腰三角形的两个底角相等，其逆命题：有两个角相等的三角形是等腰三角形是真命 题； ④菱形的对角线互相垂直，其逆命题：对角线互相垂直的四边形是菱形是假命题； 故选：C． 【点评】本题主要考查了写一个命题的逆命题的方法，首先要分清命题的条件与结论． 12．（3 分）阅读理解： 已知两点 M（x1，y1），N（x2，y2），则线段 MN 的中点 K（x，y）的坐标公式为：x＝ ，y＝ ．如图，已知点 O 为坐标原点，点 A（﹣3，0），⊙O 经过点 A，点 B 为弦 PA 的中点．若 点 P（a，b），则有 a，b 满足等式：a2+b2＝9． 设 B（m，n），则 m，n 满足的等式是（　　） A．m2+n2＝9 B．（ ）2+（ ）2＝9 C．（2m+3）2+（2n）2＝3 D．（2m+3）2+4n2＝9 【分析】根据中点坐标公式求得点 B 的坐标，然后代入 a，b 满足的等式． 【解答】解：∵点 A（﹣3，0），点 P（a，b），点 B（m，n）为弦 PA 的中点， ∴m＝ ，n＝ ．∴a＝2m+3，b＝2n． 又 a，b 满足等式：a2+b2＝9， ∴（2m+3）2+4n2＝9． 故选：D． 【点评】考查了坐标与图形性质，解题的关键是理解中点坐标公式，难度不大． 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 13．（3 分）﹣16 的相反数是　16　． 【分析】根据相反数的含义，可得求一个数的相反数的方法就是在这个数的前边添加 “﹣”，据此解答即可． 【解答】解：﹣16 的相反数是 16． 故答案为：16 【点评】此题主要考查了相反数的含义以及求法，要熟练掌握，解答此题的关键是要明 确：相反数是成对出现的，不能单独存在；求一个数的相反数的方法就是在这个数的前 边添加“﹣”． 14．（3 分）若式子 在实数范围内有意义，则 x 的取值范围是　x≥108　． 【分析】根据被开方数是非负数，可得答案． 【解答】解：由 解得 x≥108， 在实数范围内有意义，得 x﹣108≥0． 故答案是：x≥108． 【点评】本题考查了二次根式有意义的条件，利用被开方数是非负数得出不等式是解题 关键． 15．（3 分）编号为 2，3，4，5，6 的乒乓球放在不透明的袋内，从中任抽一个球，抽中编 号是偶数的概率是　． 【分析】直接利用概率公式求解可得． 【解答】解：在这 5 个乒乓球中，编号是偶数的有 3 个， 所以编号是偶数的概率为 故答案为： ，．【点评】此题主要考查了概率公式，关键是掌握随机事件 A 的概率 P（A）＝事件 A 可能 出现的结果数：所有可能出现的结果数． 16．（3 分）观察一列数：﹣3，0，3，6，9，12，…，按此规律，这一列数的第 21 个数是　 57　． 【分析】根据数列中的已知数得出这列数的第 n 个数为﹣3+3（n﹣1）＝3n﹣6，据此求 解可得． 【解答】解：由题意知，这列数的第 n 个数为﹣3+3（n﹣1）＝3n﹣6， 当 n＝21 时，3n﹣6＝3×21﹣6＝57， 故答案为：57． 【点评】本题主要考查数字的变化类，解题的关键是得出数列的变化规律：每次增加 3． 17．（3 分）如图，△ABC 与△A’B’C’是以坐标原点 O 为位似中心的位似图形，若点 A（2， 2），B（3，4），C（6，1），B’（6，8），则△A’B’C’的面积为　18　． 【分析】直接利用位似图形的性质得出对应点位置进而得出答案． 【解答】解：∵△ABC 与△A’B’C’是以坐标原点 O 为位似中心的位似图形，点 A（2，2）， B（3，4），C（6，1），B’（6，8）， ∴A′（4，4），C′（12，2）， ∴△A’B’C’的面积为：6×8﹣ ×2×4﹣ ×6×6﹣ ×2×8＝18． 故答案为：18． 【点评】此题主要考查了位似变换以及三角形面积求法，正确得出对应点位置是解题关 键． 18．（3 分）四边形具有不稳定性．如图，矩形 ABCD 按箭头方向变形成平行四边形 A’B’C’D’，当变形后图形面积是原图形面积的一半时，则∠A’＝　30°　． 【分析】根据矩形和平行四边形的面积公式可知，平行四边形 A’B’C’D’的底边 AD 边上的 高等于 AD 的一半，据此可得∠A’为 30°． 【解答】解：∵ ，∴平行四边形 A’B’C’D’的底边 AD 边上的高等于 AD 的一半， ∴∠A’＝30°． 故答案为：30° 【点评】本题主要考查了四边形的不稳定性、矩形与平行四边形的面积公式、30°角所 对的直角边等于斜边的一半，熟记特殊角的三角函数值是解答本题的关键． 三、解答题（本大题共 8 小题，共 66 分，解答应写出文字说明、证明过程或演算步骤） 19．（6 分）计算：（﹣1）3+ ﹣（π﹣112）0﹣2 tan60° 【分析】根据实数的运算法则，特殊角的三角函数值，算术平方根的运算分别进行化简 即可； 【解答】解：原式＝﹣1+3﹣1﹣2 ×＝1﹣2×3＝﹣5； 【点评】本题考查实数的运算，零指数幂，特殊角的三角函数值；牢记特殊角的三角函 数值，掌握实数的运算性质是解题的关键． 20．（6 分）求式子 【分析】先根据分式的混合运算顺序和运算法则化简原式，再将 m 的值代入计算可得． 【解答】解：原式＝ （m+3）， ÷的值，其中 m＝﹣2019． •＝当 m＝2019 时， 原式＝ ×（﹣2019+3） ＝×（﹣2016） ＝﹣1512． 【点评】本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算 法则． 21．（6 分）如图，已如平行四边形 OABC 中，点 O 为坐标顶点，点 A（3，0），C（1，2）， 函数 y＝ （k≠0）的图象经过点 C． （1）求 k 的值及直线 OB 的函数表达式： （2）求四边形 OABC 的周长． 【分析】（1）根据函数 y＝ （k≠0）的图象经过点 C，可以求得 k 的值，再根据平行四 边形的性质即可求得点 B 的坐标，从而可以求得直线 OB 的函数解析式； （2）根据题目中各点的坐标，可以求得平行四边形各边的长，从而可以求得平行四边形 的周长． 【解答】解：（1）依题意有：点 C（1，2）在反比例函数 y＝ （k≠0）的图象上， ∴k＝xy＝2， ∵A（3，0） ∴CB＝OA＝3， 又 CB∥x 轴， ∴B（4，2）， 设直线 OB 的函数表达式为 y＝ ax， ∴2＝4a， ∴a＝ ，∴直线 OB 的函数表达式为 y＝ x； （2）作 CD⊥OA 于点 D， ∵C（1，2）， ∴OC＝ ，在平行四边形 OABC 中， CB＝OA＝3，AB＝OC＝ ，∴四边形 OABC 的周长为： 3+3+ 即四边形 OABC 的周长为 6+2 ＝6+2 ，．【点评】本题考查待定系数法求反比例函数解析式和一次函数解析式，反比例函数图象 上点的坐标特征、平行四边形的性质，解答本题的关键是明确题意，利用数形结合的思 想解答． 22．（8 分）如图，菱形 ABCD 中，作 BE⊥AD、CF⊥AB，分别交 AD、AB 的延长线于点 E、F． （1）求证：AE＝BF； （2）若点 E 恰好是 AD 的中点，AB＝2，求 BD 的值． 【分析】（1）由“AAS”可证△AEB≌△BFC，可得 AE＝BF； （2）由线段垂直平分线的性质可得 BD＝AB＝2． 【解答】（1）证明：四边形 ABCD 是菱形 ∴AB＝BC，AD∥BC ∴∠A＝∠CBF ∵BE⊥AD、CF⊥AB ∴∠AEB＝∠BFC＝90° ∴△AEB≌△BFC（AAS） ∴AE＝BF （2）∵E 是 AD 中点，且 BE⊥AD ∴直线 BE 为 AD 的垂直平分线 ∴BD＝AB＝2 【点评】本题考查了菱形的性质，全等三角形的判定和性质，线段垂直平分线的性质， 熟练运用菱形的性质是本题的关键． 23 ．（8 分）九年级（1）班全班 50 名同学组成五个不同的兴趣爱好小组，每人都参加且只 能参加一个小组，统计（不完全）人数如下表： 编号 人数 一二三四五a15 20 10 b已知前面两个小组的人数之比是 1：5． 解答下列问题： （1）a+b＝　5　． （2）补全条形统计图： （3）若从第一组和第五组中任选两名同学，求这两名同学是同一组的概率．（用树状图 或列表把所有 可能都列出来） 【分析】（1）由题意知 a+b＝50﹣（15+20+10）＝5； （2）a＝3，b＝50﹣（3+15+20+10）＝2，a+b＝5； （3）一共有 20 种等可能的结果，其中两名同学是同一组的有 8 种，所求概率是：P＝ ．【解答】解：（1）由题意知 a+b＝50﹣（15+20+10）＝5， 故答案为：5； （2）∵a＝3， ∴b＝50﹣（3+15+20+10）＝2， ∴a+b＝5， 故答案为 5； （2）补全图形如下： （3）由题意得 a＝3，b＝2 设 第 一 组3 位 同 学 分 别 为A1 、 A2 、 A3 ， 设 第 五 组2 位 同 学 分 别 为B1 、 B2 ， 由上图可知，一共有 20 种等可能的结果，其中两名同学是同一组的有 8 种，所求概率是： P＝ ．【点评】本题考查了统计图与概率，熟练掌握列表法与树状图求概率是解题的关键． 24．（10 分）一艘轮船在相距 90 千米的甲、乙两地之间匀速航行，从甲地到乙地顺流航行 用 6 小时，逆流航行比顺流航行多用 4 小时． （1）求该轮船在静水中的速度和水流速度； （2）若在甲、乙两地之间建立丙码头，使该轮船从甲地到丙地和从乙地到丙地所用的航 行时间相同，问甲、丙两地相距多少干米？ 【分析】（1）设该轮船在静水中的速度是 x 千米/小时，水流速度是 y 千米/小时，根据路 程＝速度×时间，即可得出关于 x，y 的二元一次方程组，解之即可得出结论； （2）设甲、丙两地相距 a 千米，则乙、丙两地相距（90﹣a）千米，根据时间＝路程÷ 速度，即可得出关于 a 的一元一次方程，解之即可得出结论． 【解答】解：（1）设该轮船在静水中的速度是 x 千米/小时，水流速度是 y 千米/小时， 依题意，得： 解得： ，．答：该轮船在静水中的速度是 12 千米/小时，水流速度是 3 千米/小时． （2）设甲、丙两地相距 a 千米，则乙、丙两地相距（90﹣a）千米， 依题意，得： ＝，解得：a＝ ．答：甲、丙两地相距 千米． 【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用，解题的关键是： （1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出一元一次 方程． 25．（10 分）如图，已知 AC、AD 是⊙O 的两条割线，AC 与⊙O 交于 B、C 两点，AD 过圆 心 O 且与⊙O 交于 E、D 两点，OB 平分∠AOC． （1）求证：△ACD∽△ABO； （2）过点 E 的切线交 AC 于 F，若 EF∥OC，OC＝3，求 EF 的值．[提示：（ +1）（ ﹣1）＝1] 【分析】（1）由题意可得∠BOE＝ ∠AOC＝∠D，且∠A＝∠A，即可证△ACD∽△ ABO； （2）由切线的性质和勾股定理可求 CD 的长，由相似三角形的性质可求 AE＝3 ，由 平行线分线段成比例可得 ，即可求 EF 的值． 【解答】证明：（1）∵OB 平分∠AOC ∴∠BOE＝ ∠AOC ∵OC＝OD ∴∠D＝∠OCD ∵∠AOC＝∠D+∠OCD ∴∠D＝ ∠AOC ∴∠D＝∠BOE，且∠A＝∠A ∴△ACD∽△ABO （2）∵EF 切⊙O 于 E ∴∠OEF＝90° ∵EF∥OC ∴∠DOC＝∠OEF＝90° ∵OC＝OD＝3 ∴CD＝ ＝3 ∵△AC D∽△ABO ∴∴∴AE＝3 ∵EF∥OC ∴∴∴EF＝6﹣3 【点评】本题考查了相似三角形的判定和性质，圆的有关知识，勾股定理，求出 AE 的长 是本题的关键． 26．（12 分）已知抛物线 y＝mx2 和直线 y＝﹣x+b 都经过点 M（﹣2，4），点 O 为坐标原点， 点 P 为抛物线上的动点，直线 y＝﹣x+b 与 x 轴、y 轴分别交于 A、B 两点． （1）求 m、b 的值； （2）当△PAM 是以 AM 为底边的等腰三角形时，求点 P 的坐标； （3）满足（2）的条件时，求 sin∠BOP 的值． 【分析】（1）根据点 M 的坐标，利用待定系数法可求出 m，b 的值； （2）由（1）可得出抛物线及直线 AB 的解析式，利用一次函数图 象上点的坐标特征可 求出点 A 的坐标，设点 P 的坐标为（x，x2），结合点 A，M 的坐标可得出 PA2，PM2 的 值，再利用等腰三角形的性质可得出关于 x 的方程，解之即可得出结论； （3）过点 P 作 PN⊥y 轴，垂足为点 N，由点 P 的坐标可得出 PN，PO 的长，再利用正 弦的定义即可求出 sin∠BOP 的值． 【解答】解：（1）将 M（﹣2，4）代入 y＝mx2，得：4＝4m， ∴m＝1； 将 M（﹣2，4）代入 y＝﹣x+b，得：4＝2+b， ∴b＝2． （2）由（1）得：抛物线的解析式为 y＝x2，直线 AB 的解析式为 y＝﹣x+2． 当 y＝0 时，﹣x+2＝0， 解得：x＝2， ∴点 A 的坐标为（2，0），OA＝2． 22设点 P 的坐标为（x，x2），则 PA2＝（2﹣x）+（0﹣x2）＝x4+x2﹣4x+4，PM2＝（﹣2﹣ x）2+（4﹣x2）2＝x4﹣7×2+4x+20． ∵△PAM 是以 AM 为底边的等腰三角形， ∴PA2＝PM2，即 x4+x2﹣4x+4＝x4﹣7×2+4x+20， 整理，得：x2﹣x﹣2＝0， 解得：x1＝﹣1，x2＝2， ∴点 P 的坐标为（﹣1，1）或（2，4）． （3）过点 P 作 PN⊥y 轴，垂足为点 N，如图所示． 当点 P 的坐标为（﹣1，1）时，PN＝1，PO＝ ∴sin∠BOP＝ 当点 P 的坐标为（2，4）时，PN＝2，PO＝ ∴sin∠BOP＝ ∴满足（2）的条件时，sin∠BOP 的值的值为 ＝，＝；＝2 ，＝．或．【点评】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、一 次函数图象上点的坐标特征、等腰三角形的性质、勾股定理以及解直角三角形，解题的 关键是：（1）根据点的坐标，利用待定系数法求出 m，b 的值；（2）利用勾股定理及等腰 三角形的性质，找出关于 x 的方程；（3）通过解直角三角形，求出 sin∠BOP 的值．