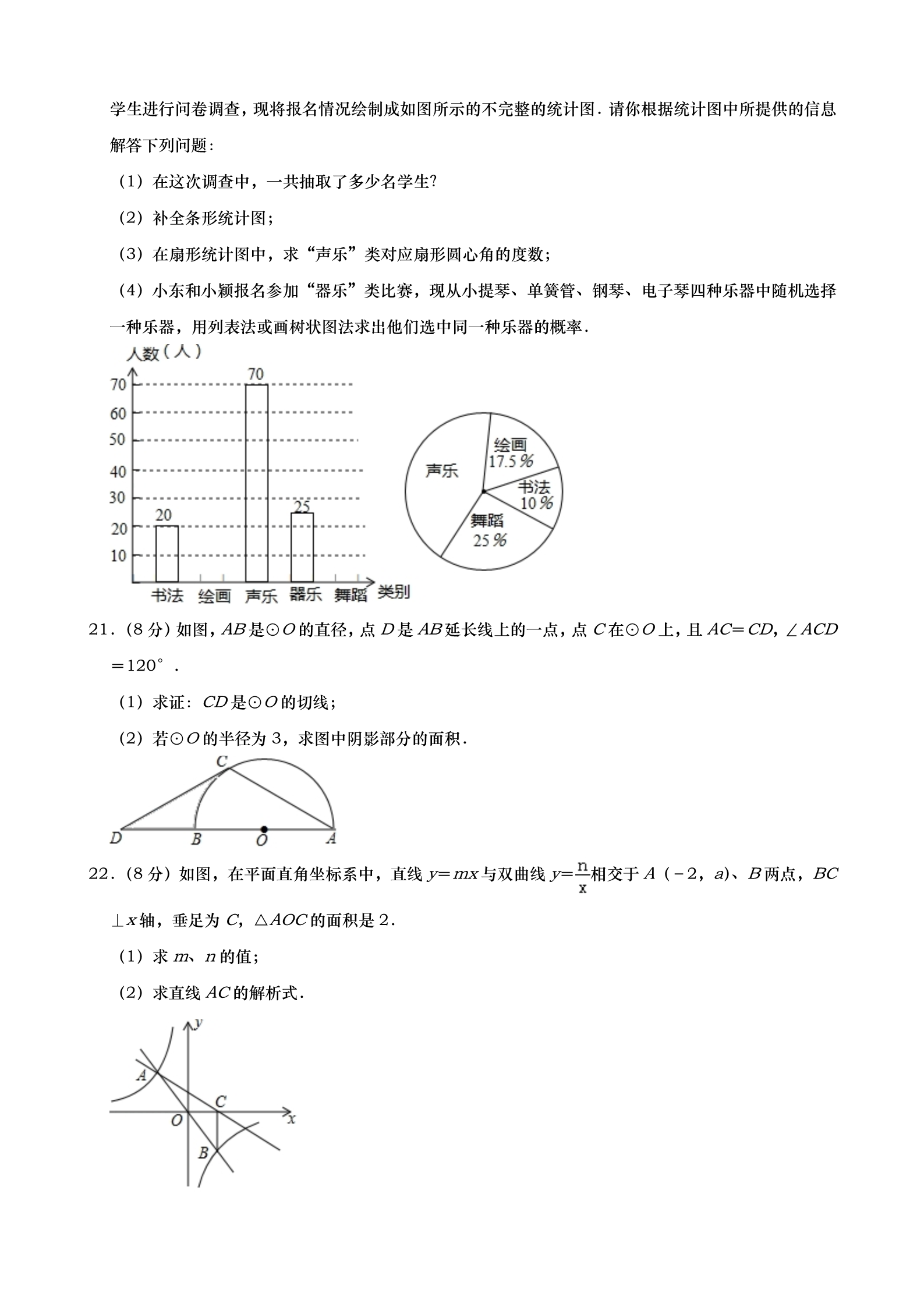
2019年山东省东营市中考数学试题（word版，含答案）

2019 年山东省东营市中考数学试卷一、选择题：本大题共 10 小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得 3 分，选错、不选或选出的答案超过一个均记零分． 1．（3 分）﹣2019 的相反数是（　　） A．﹣2019 B．2019 C．﹣ D． 2．（3 分）下列运算正确的是（　　） A．3×3﹣5×3＝﹣2x B．8×3÷4x＝2x C．＝D． +＝3．（3 分）将一副三角板（∠A＝30°，∠E＝45°）按如图所示方式摆放，使得 BA∥EF，则∠AOF 等于（　　） A．75° B．90° C．105° D．115° 4．（3 分）下列图形中，是轴对称图形的是（　　） A． C． B． D． 5．（3 分）篮球联赛中，每场比赛都要分出胜负，每队胜 1 场得 2 分，负 1 场得 1 分，某队在 10 场比赛中得到 16 分．若设该队胜的场数为 x，负的场数为 y，则可列方程组为（　　） A． C． B． D． 6．（3 分）从 1，2，3，4 中任取两个不同的数，分别记为 a 和 b，则 a2+b2＞19 的概率是（　　） A． B． C． D． 7．（3 分）如图，在 Rt△ABC 中，∠ACB＝90°，分别以点 B 和点 C 为圆心，大于 BC 的长为半径作弧，两弧相交于 D、E 两点，作直线 DE 交 AB 于点 F，交 BC 于点 G，连结 CF．若 AC＝3，CG＝ 2，则 CF 的长为（　　） A． B．3 C．2 D． 8．（3 分）甲、乙两队参加了“端午情，龙舟韵”赛龙舟比赛，两队在比赛时的路程 s（米）与时间 t（秒）之间的函数图象如图所示，请你根据图象判断，下列说法正确的是（　　） A．乙队率先到达终点 B．甲队比乙队多走了 126 米 C．在 47.8 秒时，两队所走路程相等 D．从出发到 13.7 秒的时间段内，乙队的速度慢 9．（3 分）如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点 B 出发，沿表面爬到 AC 的中点 D 处，则最短路线长为（　　） A．3 B． C．3 D．3 10．（3 分）如图，在正方形 ABCD 中，点 O 是对角线 AC、BD 的交点，过点 O 作射线 OM、ON 分别交 BC、CD 于点 E、F，且∠EOF＝90°，OC、EF 交于点 G．给出下列结论：①△COE≌△DOF； ②△OGE∽△FGC；③四边形 CEOF 的面积为正方形 ABCD 面积的；④DF2+BE2＝OG•OC．其中正确的是（　　） A．①②③④ B．①②③ C．①②④ D．③④ 二、填空题：本大题共 8 小题，其中 11-14 题每小题 3 分，15-18 题每小题 3 分，共 28 分．只要求填写最后结果． 11．（3 分）2019 年 1 月 12 日，“五指山”舰正式入列服役，是我国第六艘 071 型综合登陆舰艇，满载排水量超过 20000 吨，20000 用科学记数法表示为　 12．（3 分）因式分解：x（x﹣3）﹣x+3＝　．　． 13．（3 分）东营市某中学为积极响应“书香东营，全民阅读”活动，助力学生良好阅读习惯的养成，形成浓厚的阅读氛围，随机调查了部分学生平均每天的阅读时间，统计结果如表所示，则在本次调查中，学生阅读时间的中位数是　时间（小时） 0.5 人数（人） 12 22 10 　． 11.5 252.5 314．（3 分）已知等腰三角形的底角是 30°，腰长为 2 ，则它的周长是　　． 15．（4 分）不等式组的解集为　　． 16．（4 分）如图，AC 是⊙O 的弦，AC＝5，点 B 是⊙O 上的一个动点，且∠ABC＝45°，若点 M、N 分别是 AC、BC 的中点，则 MN 的最大值是　． 17．（4 分）如图，在平面直角坐标系中，△ACE 是以菱形 ABCD 的对角线 AC 为边的等边三角形，AC＝ 2，点 C 与点 E 关于 x 轴对称，则点 D 的坐标是　　． 18．（4 分）如图，在平面直角坐标系中，函数 y＝的点 A1（1， x 和 y＝﹣ x 的图象分别为直线 l1，l2，过 l1 上）作 x 轴的垂线交 l2 于点 A2，过点 A2 作 y 轴的垂线交 l1 于点 A3，过点 A3 作 x 轴的垂线交 l2 于点 A4，…依次进行下去，则点 A2019 的横坐标为　　．三、解答题：本大题共 7 小题，共 62 分．解答要写出必要的文字说明、证明过程或演算步骤． 19．（8 分）（1）计算：（）﹣1+（3.14﹣π）0+|2 ﹣|+2sin45°﹣ ；（2）化简求值：（ ﹣）÷ ，当 a＝﹣1 时，请你选择一个适当的数作为 b 的值，代入求值． 20．（8 分）为庆祝建国 70 周年，东营市某中学决定举办校园艺术节．学生从“书法”、“绘画”、“声乐”、 “器乐”、“舞蹈”五个类别中选择一类报名参加．为了了解报名情况，组委会在全校随机抽取了若干名学生进行问卷调查，现将报名情况绘制成如图所示的不完整的统计图．请你根据统计图中所提供的信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？（2）补全条形统计图；（3）在扇形统计图中，求“声乐”类对应扇形圆心角的度数；（4）小东和小颖报名参加“器乐”类比赛，现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器，用列表法或画树状图法求出他们选中同一种乐器的概率． 21．（8 分）如图，AB 是⊙O 的直径，点 D 是 AB 延长线上的一点，点 C 在⊙O 上，且 AC＝CD，∠ACD ＝120°．（1）求证：CD 是⊙O 的切线；（2）若⊙O 的半径为 3，求图中阴影部分的面积． 22．（8 分）如图，在平面直角坐标系中，直线 y＝mx 与双曲线 y＝相交于A（﹣2，a）、B 两点，BC ⊥x 轴，垂足为 C，△AOC 的面积是 2．（1）求 m、n 的值；（2）求直线 AC 的解析式． 23．（8 分）为加快新旧动能转换，提高公司经济效益，某公司决定对近期研发出的一种电子产品进行降价促销，使生产的电子产品能够及时售出，根据市场调查：这种电子产品销售单价定为 200 元时，每天可售出 300 个；若销售单价每降低 1 元，每天可多售出 5 个．已知每个电子产品的固定成本为 100 元，问这种电子产品降价后的销售单价为多少元时，公司每天可获利 32000 元？ 24．（10 分）如图 1，在 Rt△ABC 中，∠B＝90°，AB＝4，BC＝2，点 D、E 分别是边 BC、AC 的中点，连接 DE．将△CDE 绕点 C 逆时针方向旋转，记旋转角为 α．（1）问题发现 ①当 α＝0°时，（2）拓展探究＝　　；②当 α＝180°时，＝　　．试判断：当 0°≤α＜360°时，（3）问题解决的大小有无变化？请仅就图 2 的情形给出证明． △CDE 绕点 C 逆时针旋转至 A、B、E 三点在同一条直线上时，求线段 BD 的长． 25．（12 分）已知抛物线 y＝ax2+bx﹣4 经过点 A（2，0）、B（﹣4，0），与 y 轴交于点 C．（1）求这条抛物线的解析式；（2）如图 1，点 P 是第三象限内抛物线上的一个动点，当四边形 ABPC 的面积最大时，求点 P 的坐标；（3）如图 2，线段 AC 的垂直平分线交 x 轴于点 E，垂足为 D，M 为抛物线的顶点，在直线 DE 上是否存在一点 G，使△CMG 的周长最小？若存在，求出点 G 的坐标；若不存在，请说明理由． 2019 年山东省东营市中考数学试卷参考答案与试题解析一、选择题：本大题共 10 小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得 3 分，选错、不选或选出的答案超过一个均记零分． 1．【解答】解：﹣2019 的相反数是：2019．故选：B． 2．【解答】解：A、3×3﹣5×3＝﹣2×3，故此选项错误； B、8×3÷4x＝2×2，故此选项错误； C、＝，正确； D、 +无法计算，故此选项错误．故选：C． 3．【解答】解：∵BA∥EF，∠A＝30°， ∴∠FCA＝∠A＝30°． ∵∠F＝∠E＝45°， ∴∠AOF＝∠FCA+∠F＝30°+45°＝75°．故选：A． 4．【解答】解：A、不是轴对称图形，故本选项错误； B、不是轴对称图形，故本选项错误； C、不是轴对称图形，故本选项错误； D、是轴对称图形，故本选项正确．故选：D． 5．【解答】解：设这个队胜 x 场，负 y 场，根据题意，得．故选：A． 6．【解答】解：画树状图得： ∵共有 12 种等可能的结果，任取两个不同的数，a2+b2＞19 的有 4 种结果， ∴a2+b2＞19 的概率是故选：D．＝， 7．【解答】解：由作法得 GF 垂直平分 BC， ∴FB＝FC，CG＝BG＝2，FG⊥BC， ∵∠ACB＝90°， ∴FG∥AC， ∴BF＝CF， ∴CF 为斜边 AB 上的中线， ∵AB＝＝5， ∴CF＝ AB＝故选：A．．8．【解答】解：A、由函数图象可知，甲走完全程需要 82.3 秒，乙走完全程需要 90.2 秒，甲队率先到达终点，本选项错误； B、由函数图象可知，甲、乙两队都走了 300 米，路程相同，本选项错误； C、由函数图象可知，在 47.8 秒时，两队所走路程相等，均无 174 米，本选项正确； D、由函数图象可知，从出发到 13.7 秒的时间段内，甲队的速度慢，本选项错误；故选：C． 9．【解答】解：如图将圆锥侧面展开，得到扇形 ABB′，则线段 BF 为所求的最短路程．设∠BAB′＝n°． ∵＝4π， ∴n＝120 即∠BAB′＝120°． ∵E 为弧 BB′中点， ∴∠AFB＝90°，∠BAF＝60°， ∴BF＝AB•sin∠BAF＝6× ＝3 ，∴最短路线长为 3 故选：D．．10．【解答】解：①∵四边形 ABCD 是正方形， ∴OC＝OD，AC⊥BD，∠ODF＝∠OCE＝45°， ∵∠MON＝90°， ∴∠COM＝∠DOF， ∴△COE≌△DOF（ASA），故①正确； ②∵∠EOF＝∠ECF＝90°， ∴点 O、E、C、F 四点共圆， ∴∠EOG＝∠CFG，∠OEG＝∠FCG， ∴OGE∽△FGC，故②正确； ③∵△COE≌△DOF， ∴S△COE＝S△DOF ，∴，故③正确； ④）∵△COE≌△DOF， ∴OE＝OF，又∵∠EOF＝90°， ∴△EOF 是等腰直角三角形， ∴∠OEG＝∠OCE＝45°， ∵∠EOG＝∠COE， ∴△OEG∽△OCE， ∴OE：OC＝OG：OE， ∴OG•OC＝OE2， ∵OC＝ AC，OE＝ ∴OG•AC＝EF2， EF， ∵CE＝DF，BC＝CD， ∴BE＝CF，又∵Rt△CEF 中，CF2+CE2＝EF2， ∴BE2+DF2＝EF2， ∴OG•AC＝BE2+DF2，故④错误，故选：B．二、填空题：本大题共 8 小题，其中 11-14 题每小题 3 分，15-18 题每小题 3 分，共 28 分．只要求填写最后结果． 11．【解答】解：20000 用科学记数法表示为 2×104．故答案是：2×104． 12．【解答】解：原式＝x（x﹣3）﹣（x﹣3）＝（x﹣1）（x﹣3），故答案为：（x﹣1）（x﹣3） 13．【解答】解：由统计表可知共有：12+22+10+5+3＝52 人，中位数应为第 26 与第 27 个的平均数，而第 26 个数和第 27 个数都是 1，则中位数是 1．故答案为：1． 14．【解答】解：作 AD⊥BC 于 D， ∵AB＝AC， ∴BD＝DC，在 Rt△ABD 中，∠B＝30°， ∴AD＝ AB＝，由勾股定理得，BD＝ ∴BC＝2BD＝6，＝3， ∴△ABC 的周长为：6+2 +2 ＝6+4 故答案为：6+4 ，．15．【解答】解：解不等式 x﹣3（x﹣2）＞4，得：x＜1，解不等式，得：x≥﹣7， ≤则不等式组的解集为﹣7≤x＜1，故答案为：﹣7≤x＜1． 16．【解答】解：∵点 M，N 分别是 BC，AC 的中点， ∴MN＝ AB， ∴当 AB 取得最大值时，MN 就取得最大值，当 AB 是直径时，AB 最大，连接 AO 并延长交⊙O 于点 B′，连接 CB′， ∵AB′是⊙O 的直径， ∴∠ACB′＝90°． ∵∠ABC＝45°，AC＝5， ∴∠AB′C＝45°， ∴AB′＝＝＝5 ，∴MN 最大＝．故答案为：．17．【解答】解：如图， ∵△ACE 是以菱形 ABCD 的对角线 AC 为边的等边三角形，AC＝2， ∴CH＝1， ∴AH＝，∵∠ABO＝∠DCH＝30°， ∴DH＝AO＝ ∴OD＝，﹣﹣＝，∴点 D 的坐标是（，0）．故答案为：（，0）． 18．【解答】解：由题意可得， A1（1，），A2（1，﹣ ），A3（﹣3，﹣ ），A4（﹣3，3 ），A5（9，3 ），A6（9，﹣ ），…， 9可得 A2n+1 的横坐标为（﹣3）n ∵2019＝2×1009+1， ∴点 A2019 的横坐标为：（﹣3）1009＝﹣31009 ，故答案为：﹣31009 三、解答题：本大题共 7 小题，共 62 分．解答要写出必要的文字说明、证明过程或演算步骤． 19．【解答】解：（1）原式＝2019+1+ +2×﹣2 ．＝2020+2 ＝2020； ﹣+﹣2 （2）原式＝ •＝＝，当 a＝﹣1 时，取 b＝2，原式＝＝1． 20．【解答】解：（1）∵被抽到的学生中，报名“书法”类的人数有 20 人，占整个被抽取到学生总数的 10%， ∴在这次调查中，一共抽取了学生为：20÷10%＝200（人）；（2）被抽到的学生中，报名“绘画”类的人数为：200×17.5%＝35（人），报名“舞蹈”类的人数为：200×25%＝50（人）；补全条形统计图如下：（3）被抽到的学生中，报名“声乐”类的人数为 70 人， ∴扇形统计图中，“声乐”类对应扇形圆心角的度数为： ×360°＝126°；（4）设小提琴、单簧管、钢琴、电子琴四种乐器分别为 A、B、C、D，画树状图如图所示：共有 16 个等可能的结果，小东和小颖选中同一种乐器的结果有 4 个， ∴小东和小颖选中同一种乐器的概率为＝． 21．【解答】（1）证明：连接 OC． ∵AC＝CD，∠ACD＝120°， ∴∠A＝∠D＝30°． ∵OA＝OC， ∴∠ACO＝∠A＝30°． ∴∠OCD＝∠ACD﹣∠ACO＝90°．即 OC⊥CD， ∴CD 是⊙O 的切线．（2）解：∵∠A＝30°， ∴∠COB＝2∠A＝60°． ∴S 扇形 BOC ＝，在 Rt△OCD 中，CD＝OC ，∴，∴，∴图中阴影部分的面积为．22．【解答】解：（1）∵直线 y＝mx 与双曲线 y＝相交于A（﹣2，a）、B 两点， ∴点 A 与点 B 关于原点中心对称， ∴B（2，﹣a）， ∴C（2，0）； ∵S△AOC＝2， ∴ ×2×a＝2，解得 a＝2， ∴A（﹣2，2），把 A（﹣2，2）代入 y＝mx 和 y＝得﹣2m＝2，2＝，解得 m＝﹣1，n＝﹣4；（2）设直线 AC 的解析式为 y＝kx+b， ∵直线 AC 经过 A、C， ∴，解得 ∴直线 AC 的解析式为 y＝﹣ x+1． 23．【解答】解：设降价后的销售单价为 x 元，则降价后每天可售出[300+5（200﹣x）]个，依题意，得：（x﹣100）[300+5（200﹣x）]＝32000，整理，得：x2﹣360x+32400＝0，解得：x1＝x2＝180． 180＜200，符合题意．答：这种电子产品降价后的销售单价为 180 元时，公司每天可获利 32000 元． 24．【解答】解：（1）①当 α＝0°时， ∵Rt△ABC 中，∠B＝90°， ∴AC＝＝＝2 ，∵点 D、E 分别是边 BC、AC 的中点， ∴AE＝ AC＝，BD＝ BC＝1， ∴＝．②如图 1﹣1 中，当 α＝180°时，可得 AB∥DE， ∵∴＝＝，＝．故答案为：① ，② ．（2）如图 2，当 0°≤α＜360°时，的大小没有变化， ∵∠ECD＝∠ACB， ∴∠ECA＝∠DCB，又∵ ∴△ECA∽△DCB，．．（3）①如图 3﹣1 中，当点 E 在 AB 的延长线上时，＝＝，∴＝＝在 Rt△BCE 中，CE＝，BC＝2， ∴BE＝＝1， ∴AE＝AB+BE＝5，＝∵＝，∴BD＝＝．②如图 3﹣2 中，当点 E 在线段 AB 上时，易知 BE＝1，AE＝4﹣1＝3， ∵＝，∴BD＝综上所述，满足条件的 BD 的长为 25．【解答】解：（1）∵抛物线 y＝ax+bx﹣4 经过点 A（﹣2，0），B（4，0），，．∴，解得，∴抛物线解析式为 y＝ x2﹣x﹣4；（2）如图 1，连接 OP，设点 P（x，），其中﹣4＜x＜0，四边形 ABPC 的面积为 S，由题意得 C（0，﹣4）， ∴S＝S△AOC+S△OCP+S△OBP ＝+，＝4﹣2x﹣x2﹣2x+8，＝﹣x2﹣4x+12，＝﹣（x+2）2+16． ∵﹣1＜0，开口向下，S 有最大值， ∴当 x＝﹣2 时，四边形 ABPC 的面积最大，此时，y＝﹣4，即 P（﹣2，﹣4）．因此当四边形 ABPC 的面积最大时，点 P 的坐标为（﹣2，﹣4）．（3），∴顶点 M（﹣1，﹣ ）．如图 2，连接 AM 交直线 DE 于点 G，此时，△CMG 的周长最小．设直线 AM 的解析式为 y＝kx+b，且过点 A（2，0），M（﹣1，﹣ ）， ∴，∴直线 AM 的解析式为 y＝ ﹣3．在 Rt△AOC 中，＝2 ．∵D 为 AC 的中点， ∴，∵△ADE∽△AOC， ∴∴，，∴AE＝5， ∴OE＝AE﹣AO＝5﹣2＝3， ∴E（﹣3，0），由图可知 D（1，﹣2）设直线 DE 的函数解析式为 y＝mx+n， ∴，解得：，∴直线 DE 的解析式为 y＝﹣ ﹣ ． ∴，解得：，∴G（）．