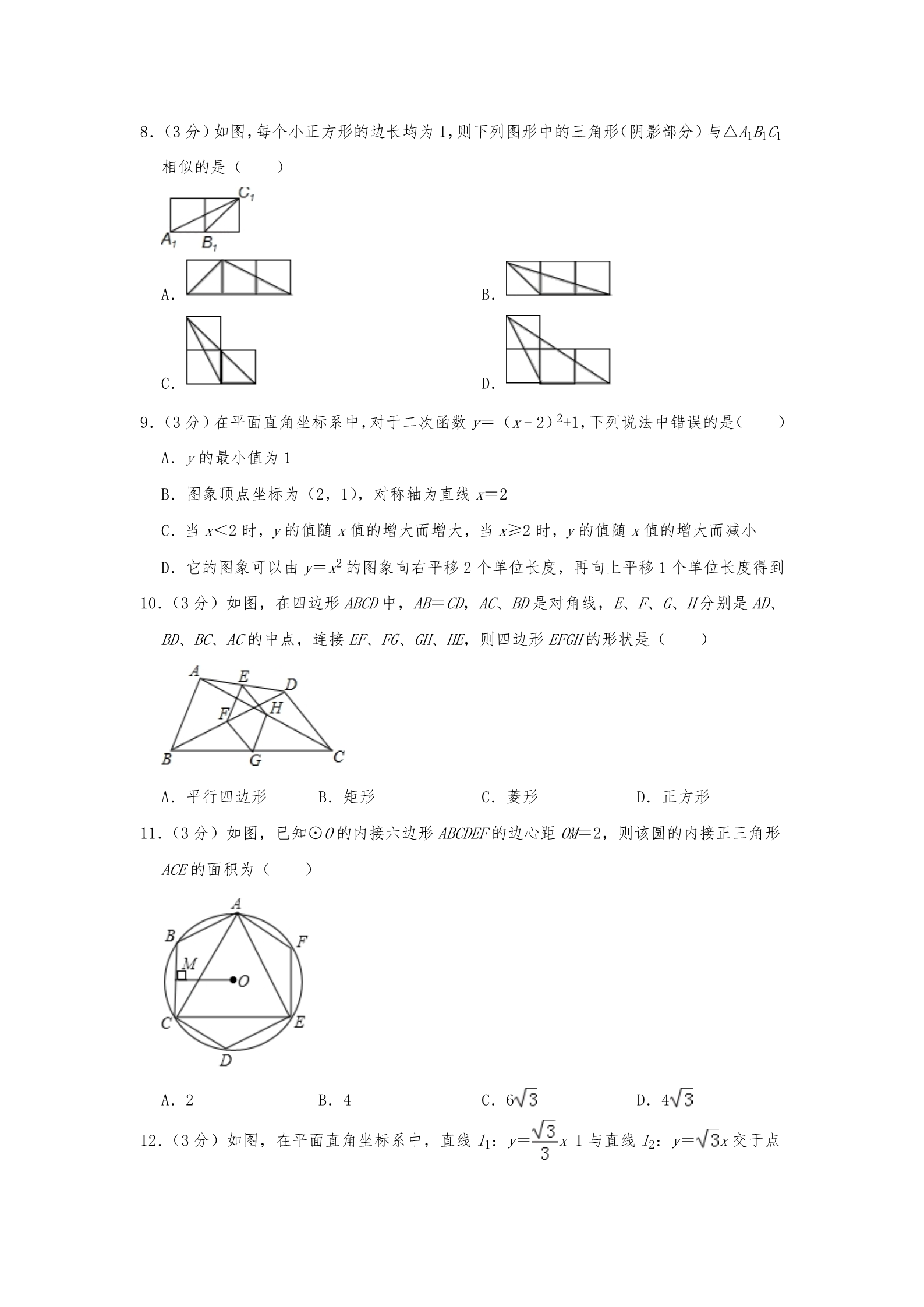
2019年四川省雅安市中考数学试题（Word版，含解析）

2019 年四川省雅安市中考数学试卷一、选择题：本大题共 12 小题，每小题 3 分，共 36 分．不需写出解答过程，请把最后结果填在题后括号内． 1．（3分）﹣2019的倒数是（　　） A．﹣2019 2．（3分）32的结果等于（　　） A．9 B．﹣9 B．2019 C．﹣ D． C．5 D．6 3．（3分）如图是下面哪个图形的俯视图（　　） A． B． C． D． 4．（3分）不等式组的解集为（　　） A．6≤x＜8 B．6＜x≤8 C．2≤x＜4 D．2＜x≤8 5．（3分）已知一组数据 5，4，x，3，9的平均数为 5，则这组数据的中位数是（　　） A．3 B．4 C．5 D．6 6．（3分）下列计算中，正确的是（　　） A．a4+a4＝a8 B．a4•a4＝2a4 C．（a3）4•a2＝a14 D．（2x2y）3÷6x3y2＝x3y 7．（3分）若 a：b＝3：4，且 a+b＝14，则 2a﹣b 的值是（　　） A．4 B．2 C．20 D．14 8．（3分）如图，每个小正方形的边长均为 1，则下列图形中的三角形（阴影部分）与△A1B1C1 相似的是（　　） A． C． B． D． 29．（3分）在平面直角坐标系中，对于二次函数 y＝（x﹣2）+1，下列说法中错误的是（　　） A．y 的最小值为 1 B．图象顶点坐标为（2，1），对称轴为直线 x＝2 C．当 x＜2时，y 的值随 x 值的增大而增大，当 x≥2时，y 的值随 x 值的增大而减小 D．它的图象可以由 y＝x2的图象向右平移 2个单位长度，再向上平移 1个单位长度得到 10．（3分）如图，在四边形 ABCD 中，AB＝CD，AC、BD 是对角线，E、F、G、H 分别是 AD、 BD、BC、AC 的中点，连接 EF、FG、GH、HE，则四边形 EFGH 的形状是（　　） A．平行四边形 B．矩形 C．菱形 D．正方形 11．（3分）如图，已知⊙O 的内接六边形 ABCDEF 的边心距 OM＝2，则该圆的内接正三角形 ACE 的面积为（　　） A．2 B．4 C．6 D．4 12．（3分）如图，在平面直角坐标系中，直线 l1：y＝ x+1与直线 l2：y＝ x 交于点 A1，过 A1作 x 轴的垂线，垂足为 B1，过 B1作 l2的平行线交 l1于 A2，过 A2作 x 轴的垂线，垂足为 B2，过 B2作 l2的平行线交 l1于 A3，过 A3作 x 轴的垂线，垂足为 B3…按此规律，则点 An 的纵坐标为（　　） nA．（）B．（）n+1 C．（）n﹣1+ D．二、填空题：本大题共 5 小题，每小题 3 分，共 15 分．不需写出解答过程，请把最后结果填在题中横线上． 13．（3分）在 Rt△ABC 中，∠C＝90°，AB＝5，BC＝4，则 sinA＝　 14．（3分）化简 x2﹣（x+2）（x﹣2）的结果是　　．　． 15．（3 分）如图，△ABC 内接于⊙O，BD 是⊙O 的直径，∠CBD＝21°，则∠A 的度数为　． 16．（3分）在两个暗盒中，各自装有编号为 1，2，3的三个球，球除编号外无其它区别，则在两个暗盒中各取一个球，两球上的编号的积为偶数的概率为　． 17．（3分）已知函数 y＝的图象如图所示，若直线 y＝x+m 与该图象恰有三个不同的交点，则 m 的取值范围为　．三、解答题（本大题共 7 小题，满分 69 分，解答应写出文字说明、证明过程或演算步骤） 18．（10分）（1）计算：|﹣2|+ ﹣20190﹣2sin30° （2）先化简，再求值：（ ﹣）÷ ，其中 a＝1． 19．（9分）某校为了解本校学生对课后服务情况的评价，随机抽取了部分学生进行调查，根据调查结果制成了如下不完整的统计图．根据统计图：（1）求该校被调查的学生总数及评价为“满意”的人数；（2）补全折线统计图；（3）根据调查结果，若要在全校学生中随机抽 1名学生，估计该学生的评价为“非常满意”或“满意”的概率是多少？ 20．（9分）某超市计划购进甲、乙两种商品，两种商品的进价、售价如下表：商品甲乙x进价（元/件）售价（元/件） x+60 200 100 若用 360元购进甲种商品的件数与用 180元购进乙种商品的件数相同．（1）求甲、乙两种商品的进价是多少元？（2）若超市销售甲、乙两种商品共 50件，其中销售甲种商品为 a 件（a≥30），设销售完 50件甲、乙两种商品的总利润为 w 元，求 w 与 a 之间的函数关系式，并求出 w 的最小值． 21．（10分）如图，▱ABCD 的对角线 AC、BD 相交于点 O，EF 经过 O，分别交 AB、CD 于点 E、 F，EF 的延长线交 CB 的延长线于 M．（1）求证：OE＝OF；（2）若 AD＝4，AB＝6，BM＝1，求 BE 的长． 22．（9分）如图，在平面直角坐标系中，一次函数 y＝﹣x+m 的图象与反比例函数 y＝（x ＞0）的图象交于 A、B 两点，已知 A（2，4）（1）求一次函数和反比例函数的解析式；（2）求 B 点的坐标；（3）连接 AO、BO，求△AOB 的面积． 23．（10分）如图，已知 AB 是⊙O 的直径，AC，BC 是⊙O 的弦，OE∥AC 交 BC 于 E，过点 B 作⊙O 的切线交 OE 的延长线于点 D，连接 DC 并延长交 BA 的延长线于点 F．（1）求证：DC 是⊙O 的切线；（2）若∠ABC＝30°，AB＝8，求线段 CF 的长． 24．（12分）已知二次函数 y＝ax2（a≠0）的图象过点（2，﹣1），点 P（P 与 O 不重合）是图象上的一点，直线 l 过点（0，1）且平行于 x 轴．PM⊥l 于点 M，点 F（0，﹣1）．（1）求二次函数的解析式；（2）求证：点 P 在线段 MF 的中垂线上；（3）设直线 PF 交二次函数的图象于另一点 Q，QN⊥l 于点 N，线段 MF 的中垂线交 l 于点 R，求的值；（4）试判断点 R 与以线段 PQ 为直径的圆的位置关系． 2019 年四川省雅安市中考数学试卷参考答案与试题解析一、选择题：本大题共 12 小题，每小题 3 分，共 36 分．不需写出解答过程，请把最后结果填在题后括号内． 1．（3分）﹣2019的倒数是（　　） A．﹣2019 B．2019 C．﹣ D．【分析】直接利用倒数的定义得出答案．【解答】解：﹣2019的倒数是：﹣ 故选：C．．【点评】此题主要考查了倒数，正确把握倒数的定义是解题关键． 2．（3分）32的结果等于（　　） A．9 B．﹣9 C．5 D．6 【分析】根据乘方的意义可得：32＝3×3＝9；【解答】解：32＝3×3＝9；故选：A．【点评】本题考查有理数的乘方；熟练掌握乘方的运算法则是解题的关键． 3．（3分）如图是下面哪个图形的俯视图（　　） A． C． B． D．【分析】根据各选项的俯视图进行判断即可．【解答】解：A．球的俯视图为一个圆（不含圆心），不合题意； B．圆柱的俯视图为一个圆（不含圆心），不合题意； C．圆台的俯视图为两个同心圆，不合题意； D．圆锥的俯视图为一个圆（含圆心），符合题意；故选：D．【点评】本题主要考查了简单几何体的三视图，俯视图是从上往下看得到的平面图形． 4．（3分）不等式组 A．6≤x＜8 的解集为（　　） B．6＜x≤8 C．2≤x＜4 D．2＜x≤8 【分析】分别解出两不等式的解集，再求其公共解．【解答】解：由①得 x＞6，由②得 x≤8， ∴不等式组的解集为 6＜x≤8，故选：B．【点评】本题考查了解一元一次方程组，求不等式组的解集应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了． 5．（3分）已知一组数据 5，4，x，3，9的平均数为 5，则这组数据的中位数是（　　） A．3 B．4 C．5 D．6 【分析】先根据平均数的定义求出 x 的值，再把这组数据从小到大排列，然后求出最中间两个数的平均数即可．【解答】解：∵5，4，x，3，9的平均数为 5， ∴（5+4+x+3+9）÷5＝5，解得：x＝4，把这组数据从小到大排列为：3，4，4，5，9，则这组数据的中位数是 4；故选：B．【点评】此题考查了平均数与中位数，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，关键是求出 x 的值． 6．（3分）下列计算中，正确的是（　　） A．a4+a4＝a8 B．a4•a4＝2a4 C．（a3）4•a2＝a14 D．（2x2y）3÷6x3y2＝x3y 【分析】直接利用合并同类项法则以及同底数幂的乘除运算法则、积的乘方运算法则分别化简得出答案．【解答】解：A、a4+a4＝2a4，故此选项错误； B、a4•a4＝a8，故此选项错误； C、（a3）4•a2＝a14 ，正确； D、（2x2y）3÷6x3y2＝8x6y3÷6x3y2＝ x3y，故此选项错误；故选：C．【点评】此题主要考查了整式的混合运算，正确掌握相关运算法则是解题关键． 7．（3分）若 a：b＝3：4，且 a+b＝14，则 2a﹣b 的值是（　　） A．4 B．2 C．20 D．14 【分析】根据比例的性质得到 3b＝4a，结合 a+b＝14求得 a、b 的值，代入求值即可．【解答】解：由 a：b＝3：4知 3b＝4a，所以 b＝．所以由 a+b＝14得到：a+ ＝14，解得 a＝6．所以 b＝8．所以 2a﹣b＝2×6﹣8＝4．故选：A．【点评】考查了比例的性质，内项之积等于外项之积．若＝，则ad＝bc． 8．（3分）如图，每个小正方形的边长均为 1，则下列图形中的三角形（阴影部分）与△A1B1C1 相似的是（　　） A． C． B． D．【分析】根据相似三角形的判定方法一一判断即可．【解答】解：因为△A1B1C1中有一个角是 135°，选项中，有 135°角的三角形只有 B，且满足两边成比例夹角相等，故选：B．【点评】本题考查相似三角形的性质，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型． 29．（3分）在平面直角坐标系中，对于二次函数 y＝（x﹣2）+1，下列说法中错误的是（　　） A．y 的最小值为 1 B．图象顶点坐标为（2，1），对称轴为直线 x＝2 C．当 x＜2时，y 的值随 x 值的增大而增大，当 x≥2时，y 的值随 x 值的增大而减小 D．它的图象可以由 y＝x2的图象向右平移 2个单位长度，再向上平移 1个单位长度得到【分析】根据题目中的函数解析式，可以判断各个选项中的说法是否正确．【解答】解：二次函数 y＝（x﹣2）2+1，a＝1＞0， ∴该函数的图象开口向上，对称轴为直线 x＝2，顶点为（2，1），当 x＝2时，y 有最小值 1，当 x＞2时，y 的值随 x 值的增大而增大，当 x＜2时，y 的值随 x 值的增大而减小；故选项 A、B 的说法正确，C 的说法错误； 2根据平移的规律，y＝x2的图象向右平移 2个单位长度得到 y＝（x﹣2），再向上平移 1 个单位长度得到 y＝（x﹣2）2+1；故选项 D 的说法正确，故选：C．【点评】本题考查二次函数的性质、二次函数的最值，二次函数图象与几何变换，解答本题的关键是明确题意，利用二次函数的性质解答． 10．（3分）如图，在四边形 ABCD 中，AB＝CD，AC、BD 是对角线，E、F、G、H 分别是 AD、 BD、BC、AC 的中点，连接 EF、FG、GH、HE，则四边形 EFGH 的形状是（　　） A．平行四边形 B．矩形 C．菱形 D．正方形【分析】根据三角形的中位线定理可得，EH 平行且等于 CD 的一半，FG 平行且等于 CD 的一半，根据等量代换和平行于同一条直线的两直线平行，得到 EH 和 FG 平行且相等，所以 EFGH 为平行四边形，又因为 EF 等于 AB 的一半且 AB＝CD，所以得到所证四边形的邻边 EH 与 EF 相等，所以四边形 EFGH 为菱形．【解答】解：∵E、F、G、H 分别是 AD、BD、BC、AC 的中点， ∴在△ADC 中，EH 为△ADC 的中位线，所以 EH∥CD 且 EH＝ CD；同理 FG∥CD 且 FG＝ CD，同理可得 EF＝ AB，则 EH∥FG 且 EH＝FG， ∴四边形 EFGH 为平行四边形，又 AB＝CD，所以 EF＝EH， ∴四边形 EFGH 为菱形．故选：C．【点评】此题考查学生灵活运用三角形的中位线定理，平行四边形的判断及菱形的判断进行证明，是一道综合题． 11．（3分）如图，已知⊙O 的内接六边形 ABCDEF 的边心距 OM＝2，则该圆的内接正三角形 ACE 的面积为（　　） A．2 B．4 C．6 D．4 【分析】连接 OC、OB，过 O 作 ON⊥CE 于 N，证出△COB 是等边三角形，根据锐角三角函数的定义求解即可．【解答】解：如图所示，连接 OC、OB，过 O 作 ON⊥CE 于 N， ∵多边形 ABCDEF 是正六边形， ∴∠COB＝60°， ∵OC＝OB， ∴△COB 是等边三角形， ∴∠OCM＝60°， ∴OM＝OC•sin∠OCM， ∴OC＝＝（cm）． ∵∠OCN＝30°， ∴ON＝ OC＝，CN＝2， ∴CE＝2CN＝4， ∴该圆的内接正三角形 ACE 的面积＝3× 故选：D．＝4 ，【点评】本题考查的是正六边形的性质、等边三角形的判定与性质、三角函数；熟练掌握正六边形的性质，由三角函数求出 OC 是解决问题的关键． 12．（3分）如图，在平面直角坐标系中，直线 l1：y＝ x+1与直线 l2：y＝ x 交于点 A1，过 A1作 x 轴的垂线，垂足为 B1，过 B1作 l2的平行线交 l1于 A2，过 A2作 x 轴的垂线，垂足为 B2，过 B2作 l2的平行线交 l1于 A3，过 A3作 x 轴的垂线，垂足为 B3…按此规律，则点 An 的纵坐标为（　　） nA．（）B．（）n+1 C．（）n﹣1+ D．【分析】联立直线 l1与直线 l2的表达式并解得：x＝，y＝，故A1（，），依，次求出：点 A2的纵坐标为、A3的纵坐标为，即可求解．【解答】解：联立直线 l1 与直线 l2 的表达式并解得：x＝，y＝，故A1（）；则点 B1（，0），则直线 B1A2的表达式为：y＝ x+b，将点 B1坐标代入上式并解得：直线 B1A2的表达式为：y3＝ x﹣ ，将表达式 y3与直线 l1的表达式联立并解得：x＝同理可得 A3的纵坐标为，y＝，即点A2的纵坐标为；，…按此规律，则点 An 的纵坐标为（）n，故选：A．【点评】本题考查了两直线的交点，要求利用图象求解各问题，要认真体会点的坐标，一次函数与一元一次方程组之间的内在联系．二、填空题：本大题共 5 小题，每小题 3 分，共 15 分．不需写出解答过程，请把最后结果填在题中横线上． 13．（3分）在 Rt△ABC 中，∠C＝90°，AB＝5，BC＝4，则 sinA＝　．【分析】根据正弦的定义解答．【解答】解：在 Rt△ABC 中，sinA＝故答案为：＝，．【点评】本题考查的是锐角三角函数的定义，锐角 A 的对边 a 与斜边 c 的比叫做∠A 的正弦，记作 sinA． 14．（3分）化简 x2﹣（x+2）（x﹣2）的结果是　4　．【分析】先根据平方差公式化简，再合并同类项即可．【解答】解：x2﹣（x+2）（x﹣2）＝x2﹣x2+4＝4．故答案为：4．【点评】本题主要考查了平方差公式，熟记公式是解答本题的关键． 15．（3分）如图，△ABC 内接于⊙O，BD 是⊙O 的直径，∠CBD＝21°，则∠A 的度数为　69 °　．【分析】直接利用圆周角定理得出∠BCD＝90°，进而得出答案．【解答】解：∵△ABC 内接于⊙O，BD 是⊙O 的直径， ∴∠BCD＝90°， ∵∠CBD＝21°， ∴∠A＝∠D＝90°﹣21°＝69°．故答案为：69° 【点评】此题主要考查了三角形的外接圆与外心，正确掌握圆周角定理是解题关键． 16．（3分）在两个暗盒中，各自装有编号为 1，2，3的三个球，球除编号外无其它区别，则在两个暗盒中各取一个球，两球上的编号的积为偶数的概率为　．【分析】画树状图展示所有 9种等可能的结果数，找出两球上的编号的积为偶数的结果数，然后根据概率公式求解．【解答】解：画树状图为：共有 9种等可能的结果数，其中两球上的编号的积为偶数的结果数为 5，所以两球上的编号的积为偶数的概率＝．故答案为．【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果 n，再从中选出符合事件 A 或 B 的结果数目 m，然后利用概率公式计算事件 A 或事件 B 的概率． 17．（3分）已知函数 y＝的图象如图所示，若直线 y＝x+m 与该图象恰有三个不同的交点，则 m 的取值范围为　0＜m＜．【分析】直线与 y＝x 有一个交点，与 y＝﹣x2+2x 有两个交点，则有 m＞0，x+m＝﹣x2+2x 时，△＝1﹣4m＞0，即可求解．【解答】解：直线 y＝x+m 与该图象恰有三个不同的交点，则直线与 y＝x 有一个交点， ∴m＞0， ∵与 y＝﹣x2+2x 有两个交点， ∴x+m＝﹣x2+2x， △＝1﹣4m＞0， ∴m＜ ∴0＜m＜故答案为 0＜m＜，；．【点评】本题考查二次函数与一次函数的图象及性质；能够根据条件，数形结合的进行分析，可以确定 m 的范围．三、解答题（本大题共 7 小题，满分 69 分，解答应写出文字说明、证明过程或演算步骤） 18．（10分）（1）计算：|﹣2|+ ﹣20190﹣2sin30° （2）先化简，再求值：（ ﹣）÷ ，其中 a＝1．【分析】（1）根据绝对值、零指数幂和特殊角的三角函数值可以解答本题；（2）根据分式的减法和除法可以化简题目中的式子，然后将 a 的值代入化简后的式子即可解答本题．【解答】解：（1）|﹣2|+ ﹣20190﹣2sin30° ＝2+3﹣1﹣2× ＝2+3﹣1﹣1 ＝3；（2）（＝[ ﹣）÷ ]＝（＝）＝，当 a＝1时，原式＝．【点评】本题考查分式的化简求值、零指数幂、特殊角的三角函数值，解答本题的关键是明确它们各自的计算方法． 19．（9分）某校为了解本校学生对课后服务情况的评价，随机抽取了部分学生进行调查，根据调查结果制成了如下不完整的统计图．根据统计图：（1）求该校被调查的学生总数及评价为“满意”的人数；（2）补全折线统计图；（3）根据调查结果，若要在全校学生中随机抽 1名学生，估计该学生的评价为“非常满意”或“满意”的概率是多少？【分析】（1）首先求得总人数，然后根据百分比求得人数即可；（2）根据（1）补全折线统计图即可；（3）利用概率公式求解即可．【解答】解：（1）由折线统计图知“非常满意”9人，由扇形统计图知“非常满意”占 15%，所以被调查学生总数为 9÷15%＝60（人），所以“满意”的人数为 60﹣（9+21+3）＝ 27（人）；（2）如图：（3）所求概率为＝．【点评】本题考查了统计图及概率公式的知识，能够从统计图中整理出进一步解题的有关信息是解答本题的关键，难度不大． 20．（9分）某超市计划购进甲、乙两种商品，两种商品的进价、售价如下表：商品甲乙x进价（元/件）售价（元/件） x+60 200 100 若用 360元购进甲种商品的件数与用 180元购进乙种商品的件数相同．（1）求甲、乙两种商品的进价是多少元？（2）若超市销售甲、乙两种商品共 50件，其中销售甲种商品为 a 件（a≥30），设销售完 50件甲、乙两种商品的总利润为 w 元，求 w 与 a 之间的函数关系式，并求出 w 的最小值．【分析】（1）根据用 360元购进甲种商品的件数与用 180元购进乙种商品的件数相同列出方程，解方程即可；（2）根据总利润＝甲种商品一件的利润×甲种商品的件数+乙种商品一件的利润×乙种商品的件数列出 w 与 a 之间的函数关系式，再根据一次函数的性质即可求出 w 的最小值．【解答】解：（1）依题意可得方程：＝，解得 x＝60，经检验 x＝60是方程的根， ∴x+60＝120元，答：甲、乙两种商品的进价分别是 120元，60元；（2）∵销售甲种商品为 a 件（a≥30）， ∴销售乙种商品为（50﹣a）件，根据题意得：w＝（200﹣120）a+（100﹣60）（50﹣a）＝40a+2000（a≥30）， ∵40＞0， ∴w 的值随 a 值的增大而增大， ∴当 a＝30时，w 最小值＝40×30+2000＝3200（元）．【点评】本题考查了分式方程的应用，一次函数的应用．解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的数量关系． 21．（10分）如图，▱ABCD 的对角线 AC、BD 相交于点 O，EF 经过 O，分别交 AB、CD 于点 E、 F，EF 的延长线交 CB 的延长线于 M．（1）求证：OE＝OF；（2）若 AD＝4，AB＝6，BM＝1，求 BE 的长．【分析】（1）根据平行四边形的性质得到 OA＝OC，AB∥CD，证明△AOE≌△COF，根据全等三角形的性质证明结论；（2）过点 O 作 ON∥BC 交 AB 于 N，根据相似三角形的性质分别求出 ON、BN，证明△ONE∽△ MBE，根据相似三角形的性质列式计算即可．【解答】（1）证明：∵四边形 ABCD 是平行四边形， ∴OA＝OC，AB∥CD，BC＝AD， ∴∠OAE＝∠OVF，在△AOE 和△COF 中，，∴△AOE≌△COF（ASA）， ∴OE＝OF；（2）解：过点 O 作 ON∥BC 交 AB 于 N，则△AON∽△ACB， ∵OA＝OC， ∴ON＝ BC＝2，BN＝ AB＝3， ∵ON∥BC， ∴△ONE∽△MBE， ∴＝，即＝，解得，BE＝1．【点评】本题考查的是相似三角形的判定和性质、平行四边形的性质，掌握相似三角形的判定定理和性质定理、全等三角形的判定定理和性质定理是解题的关键． 22．（9分）如图，在平面直角坐标系中，一次函数 y＝﹣x+m 的图象与反比例函数 y＝（x ＞0）的图象交于 A、B 两点，已知 A（2，4）（1）求一次函数和反比例函数的解析式；（2）求 B 点的坐标；（3）连接 AO、BO，求△AOB 的面积．【分析】（1）由点 A 的坐标利用一次函数、反比例函数图象上点的坐标特征即可得出反比例函数解析式；（2）联立方程，解方程组即可求得；（3）求出直线与 y 轴的交点坐标后，即可求出 S△AOD 和 S△BOD，继而求出△AOB 的面积．【解答】解：（1）将 A（2，4）代入 y＝﹣x+m 与 y＝（x＞0）中得 4＝﹣2+m，4＝ ∴m＝6，k＝8，，∴一次函数的解析式为 y＝﹣x+6，反比例函数的解析式为 y＝；（2）解方程组 ∴B（4，2）；得或，（3）设直线 y＝﹣x+6与 x 轴，y 轴交于 C，D 点，易得 D（0，6）， ∴OD＝6， ∴S△AOB＝S△DOB﹣S△AOD＝ ×6×4﹣ ×6×2＝6．【点评】本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数和反比例函数解析式以及三角形的面积，解题的关键是：根据点的坐标利用待定系数法求出函数解析式；利用分割图形求面积法求出△AOB 的面积． 23．（10分）如图，已知 AB 是⊙O 的直径，AC，BC 是⊙O 的弦，OE∥AC 交 BC 于 E，过点 B 作⊙O 的切线交 OE 的延长线于点 D，连接 DC 并延长交 BA 的延长线于点 F．（1）求证：DC 是⊙O 的切线；（2）若∠ABC＝30°，AB＝8，求线段 CF 的长．【分析】（1）连接 OC，AC，根据平行线的性质得到∠1＝∠ACB，由圆周角定理得到∠1＝∠ ACB＝90°，根据线段垂直平分线的性质得到 DB＝DC，求得∠DBE＝∠DCE，根据切线的性质得到∠DBO＝90°，求得 OC⊥DC，于是得到结论；（2）解直角三角形即可得到结论．【解答】（1）证明：连接 OC，AC， ∵OE∥AC， ∴∠1＝∠ACB， ∵AB 是⊙O 的直径， ∴∠1＝∠ACB＝90°， ∴OD⊥BC，由垂径定理得 OD 垂直平分 BC， ∴DB＝DC， ∴∠DBE＝∠DCE，又∵OC＝OB， ∴∠OBE＝∠OCE，即∠DBO＝∠OCD， ∵DB 为⊙O 的切线，OB 是半径， ∴∠DBO＝90°， ∴∠OCD＝∠DBO＝90°，即 OC⊥DC， ∵OC 是⊙O 的半径， ∴DC 是⊙O 的切线；（2）解：在 Rt△ABC 中，∠ABC＝30°， ∴∠3＝60°，又 OA＝OC， ∴△AOC 是等边三角形， ∴∠COF＝60°，在 Rt△COF 中，tan∠COF＝，∴CF＝4 ．【点评】本题考查了切线的判定和性质，垂径定理，圆周角定理，等腰三角形的性质，正确的作出辅助线是解题的关键． 24．（12分）已知二次函数 y＝ax2（a≠0）的图象过点（2，﹣1），点 P（P 与 O 不重合）是图象上的一点，直线 l 过点（0，1）且平行于 x 轴．PM⊥l 于点 M，点 F（0，﹣1）．（1）求二次函数的解析式；（2）求证：点 P 在线段 MF 的中垂线上；（3）设直线 PF 交二次函数的图象于另一点 Q，QN⊥l 于点 N，线段 MF 的中垂线交 l 于点 R，求的值；（4）试判断点 R 与以线段 PQ 为直径的圆的位置关系．【分析】（1）把点（2，﹣1）代入函数表达式，即可求解；（2）y1＝﹣ x12，即 x12＝﹣4y1，PM＝|1﹣y1|，又 PF＝＝＝|y1﹣1|＝PM，即可求解；（3）证明△PMR≌△PFR（SAS）、Rt△RFQ≌Rt△RNQ（HL），即 RN＝FR，即 MR＝FR＝RN，即可求解；（4）在△PQR 中，由（3）知 PR 平分∠MRF，QR 平分∠FRN，则∠PRQ＝（∠MRF+∠ FRN）＝90°，即可求解．【解答】解：（1）∵y＝ax2（a≠0）的图象过点（2，﹣1）， ∴﹣1＝a×22，即 a＝，∴y＝﹣ x2；（2）设二次函数的图象上的点 P（x1，y1），则 M（x1，1）， y1＝﹣ x12，即 x12＝﹣4y1，PM＝|1﹣y1|，又 PF＝＝＝|y1﹣1|＝PM，即 PF＝PM， ∴点 P 在线段 MF 的中垂线上；（3）连接 RF， ∵R 在线段 MF 的中垂线上， ∴MR＝FR，又∵PM＝PF，PR＝PR， ∴△PMR≌△PFR（SAS）， ∴∠PFR＝∠PMR＝90°， ∴RF⊥PF，连接 RQ，又在 Rt△RFQ 和 Rt△RNQ 中， ∵Q 在 y＝﹣ x2的图象上，由（2）结论知∴QF＝QN， ∵RQ＝RQ， ∴Rt△RFQ≌Rt△RNQ（HL），即 RN＝FR，即 MR＝FR＝RN， ∴＝1；（4）在△PQR 中，由（3）知 PR 平分∠MRF，QR 平分∠FRN， ∴∠PRQ＝（∠MRF+∠FRN）＝90°， ∴点 R 在以线段 PQ 为直径的圆上．【点评】本题考查的是二次函数综合运用，涉及到三角形全等、中垂线、圆的基本知识等，其中（3），证明△PMR≌△PFR（SAS）、Rt△RFQ≌Rt△RNQ（HL）是本题解题的关键．