湖南省邵阳市2018年中考数学真题试题（含答案）下载

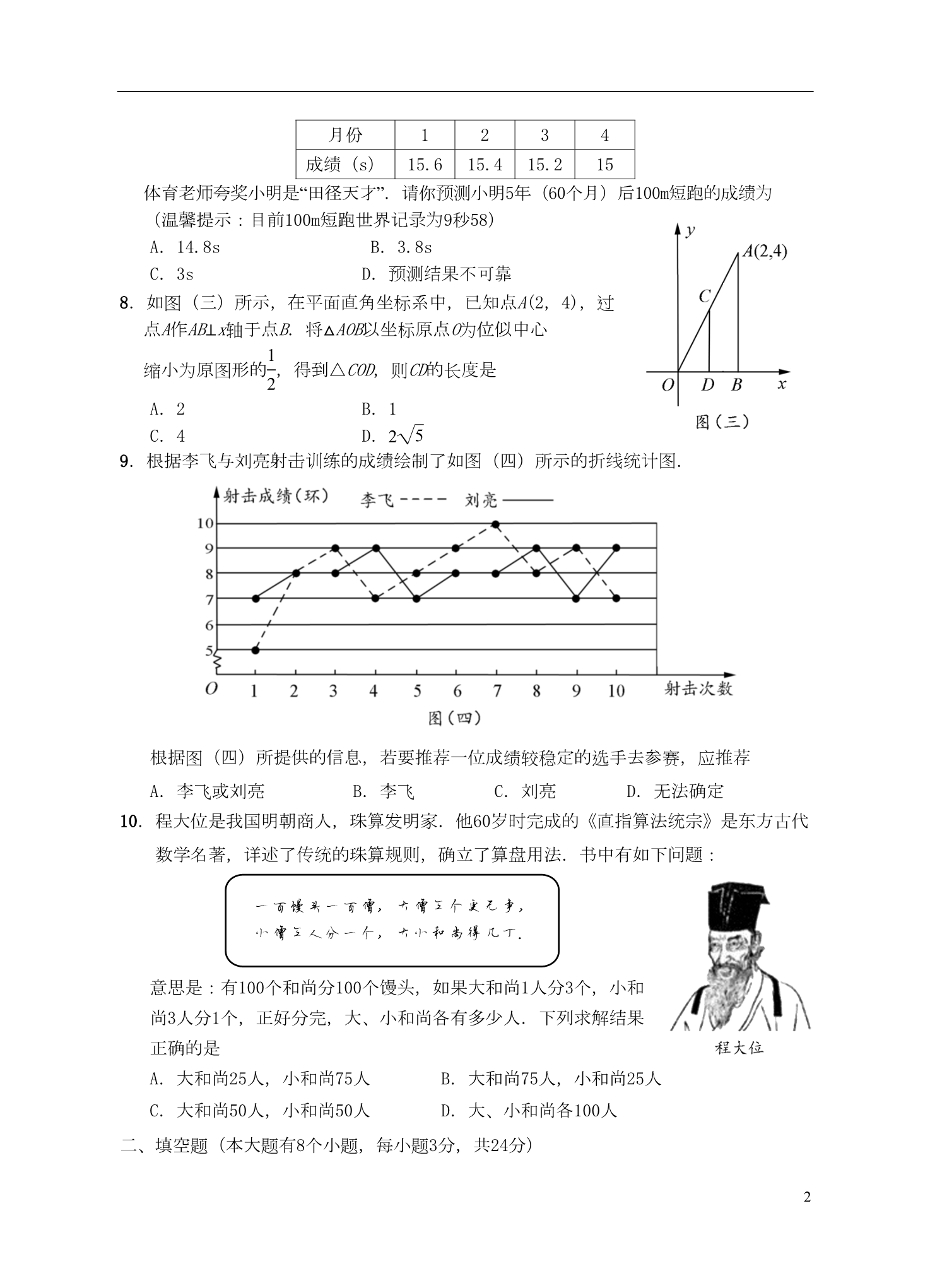
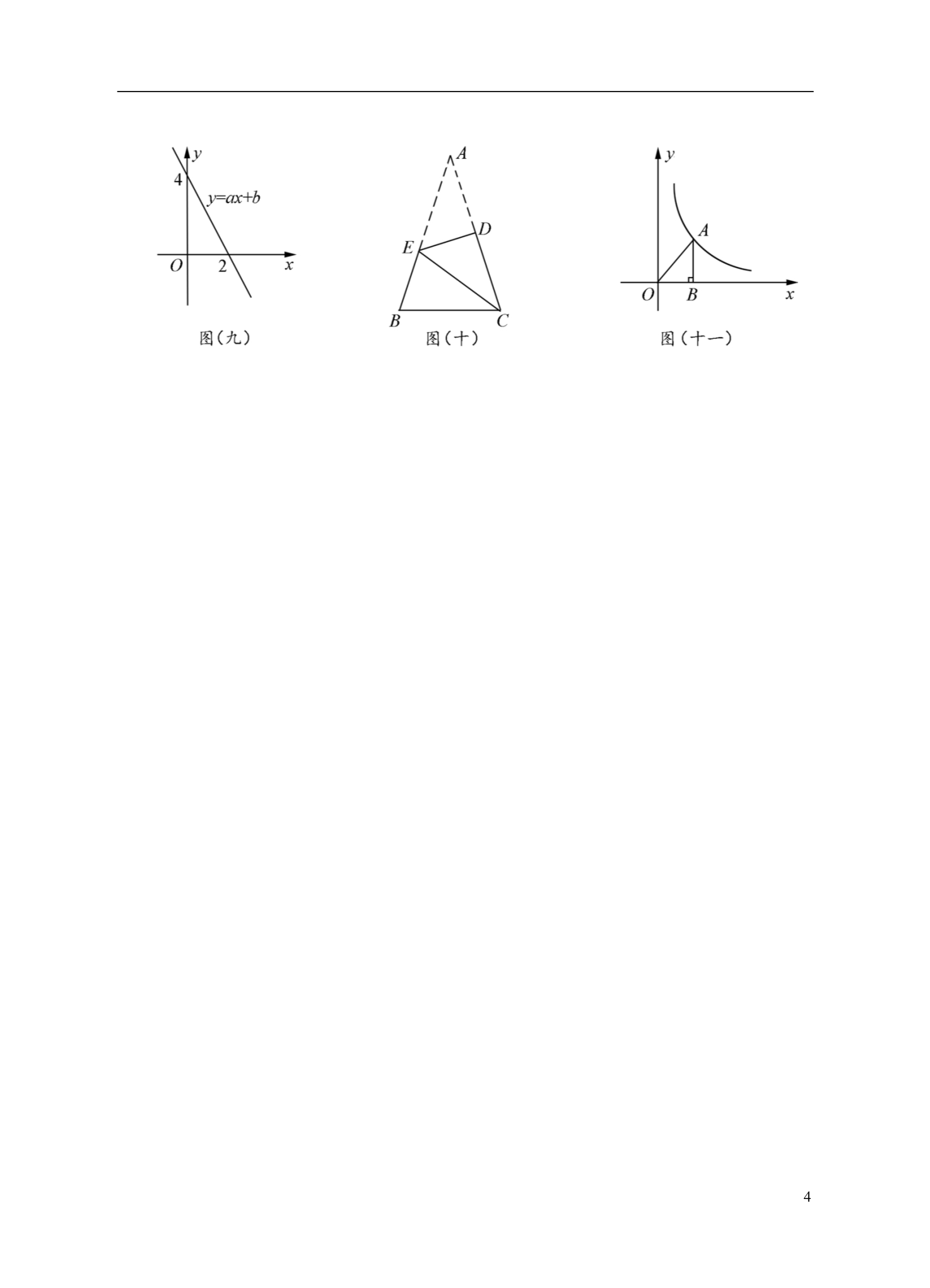
题试题 湖南省邵阳市2018年中考数学真 温馨提示： 试（1）本学科 卷分 试题 题卷和答 卡两部分，考 试时 为量 120分 钟满 为 分 120分； ，请证题（2） 你将姓名、准考 号等相关信息按要求填涂在答 卡上； 请题（3） 你在答 卡上作答，答在本 试题 卷上无效． 选择题 题题题（本大 有10个小 ，每小 3分，共30分．在每小 题给 选项 出的四个 中只有 一、 项题是符合 目要求的） 一计1．用 算器依次按 A．1.5 键结，得到的 果最接近的是 B．1.6 C．1.7 D．1.8 图 线 2．如 （一）所示，直 AB，CD相交于点O，已知 则∠AOD＝160 ， BOC的大小 为∠°°°°A．20 C．70 B．60 °D．160 3项3．将多 式x－x 因式分解正确的是 A．x(x2－1) B．x(1－x2) C．x(x＋1)(x－1) D．x(1＋x)(1－x) 图4．下列 形中，是 轴对 图称 形的是 经济 报报 电 》2018年5月21日 道：目前，世界集成 路生 产术技 水平最高已达到7n 5．据《 日－9 产线 术为陆电的技 水平 14~28nm，中国大 集成 路生 产术技 水 m（1nm＝10 m），主流生 为记平最高 28nm．将28nm用科学 数法可表示 为－9 －8 ×A．28 10m ×B．2.8 10m 98×C．28 10 m ×D．2.8 10 m 图6．如 （二）所示，四 形ABCD 边为边O的内接四 形， ⊙则∠BCD＝120 ， BOD的大小是 ∠°°°B．120 A．80 °°C．100 D．90 训练 训练 绩成 如下 7．小明参加100m短跑 ，2018年1～4月的 表所示： 1月份 1234绩成（s） 15.6 15.4 15.2 15 师奖请”预测 绩为 “小明是 田径天才 ． 体育老 夸你小明5年（60个月）后100m短跑的成 记录为 （温馨提示：目前100m短跑世界 9秒58） A．14.8s C．3s B．3.8s 预测结 D． 果不可靠 8．如图（三）所示，在平面直角坐标系中，已知点A(2，4)，过 点A作AB⊥x轴于点B．将△AOB以坐标原点O为位似中心 1缩小为原图形的 ，得到△COD，则CD的长度是 2A．2 C．4 B．1 D． 52飞9．根据李 与刘亮射 击训练 绩绘 图 线统计图 制了如 （四）所示的折． 的成 根据图（四）所提供的信息，若要推荐一位成绩较稳定的选手去参赛，应推荐 A．李飞或刘亮 B．李飞 C．刘亮 D．无法确定 岁时 东 发统10．程大位是我国明朝商人，珠算 明家．他60 完成的《直指算法 宗》是 方古代 详数学名著， 述了 传统 规则 的珠算 盘 书 ，确立了算 用法． 中有如下 问题 ：一百馒头一百僧，大僧三个更无争， 小僧三人分一个，大小和尚得几丁． 馒头 意思是：有100个和尚分100个 ，如果大和尚1人分3个，小和 结尚3人分1个，正好分完，大、小和尚各有多少人．下列求解 果正确的是 A．大和尚25人，小和尚75人 C．大和尚50人，小和尚50人 B．大和尚75人，小和尚25人 D．大、小和尚各100人 二、填空题（本大题有8个小题，每小题3分，共24分） 2轴图则11．点A在数 上的位置如 （五）所示， 点A表示的数 的相反数是 ．12．如图（六）所示，点E是平行四边形ABCD的边BC 延长线上一点，连接AE，交CD于点F，连接BF． 写出图中任意一对相似三角形： 13．已知关于x的方程x ．2＋3x－m＝0的一个解为－3， 则它的另一个解是 ．14．如图（七）所示，在四边形ABCD中，AD⊥AB， ∠C＝110°，它的一个外角∠ADE＝60°， 则∠B的大小是 ．15．某市对九年级学生进行“综合素质”评价，评价结 果分为A，B，C，D，E五个等级．现随机抽取了500名学生的评价结果作为样本进行 分析，绘制了如图（八）所示的统计图．已知图中从左到右的五个长方形的高之比为 2∶3∶3∶1∶1，据此估算该市80000名九年级学生中“综合素质”评价结果为“A”的学生约为 人． 16．如图（九）所示，一次函数y ＝ax＋b的图象 与x轴相交于点(2，0)，与y轴相交于点(0，4)． 结合图象可知，关于x的方程ax＋b＝0的解是 ．17．如图（十）所示，在等腰△ABC中，AB＝AC，∠A＝36°．将△ABC中的∠A沿DE向下翻 3折，使点A落在点C处．若AE＝ ，则BC的长是_________． k18．如图（十一）所示，点A是反比例函数y＝ 图象上一点，作AB⊥x轴，垂足为点B． x若△AOB的面积为2，则k的值是 ．34三、解答题（本大题有8个小题，第19~25题每小题8分，第26题10分，共66分．解答应写 出必要的文字说明、演算步骤或证明过程） 19．计算：(－1)2＋( π －3.14)0－| －2|． 2120．先化简，再求值：( a－2b )( a＋2b)－(a－2b)2＋8b2，其中a＝－2，b＝ ． 221．如图（十二）所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD， 垂足为点D，连结BC．BC平分∠ABD． 求证：CD为⊙O的切线． 22．某校为选拔一名选手参加“美丽邵阳，我为家乡做代言”主题演讲比赛，经研究，按图 （十三）所示的项目和权数对选拔赛参赛选手进行考评（因排版原因统计图不完整） ．下表是李明、张华在选拔赛中的得分情况： 项目 演讲 技巧 服装 普通话 主题 结合以上选手 李明 张华 85 90 70 75 80 75 85 80 信息，回答下列问题： （1）求服装项目的权数及普通话项目对应扇形的圆心角大小； （2）求李明在选拔赛中四个项目所得分数的众数和中位数； （3）根据你所学的知识，帮助学校在李明、张华两人中选择一人参加“美丽邵阳，我 5为家乡做代言”主题演讲比赛，并说明理由． 623．某公司计划购买A，B两种型号的机器人搬运材料．已知A型机器人比B型机器人每小时 多搬运30kg材料，且A型机器人搬运1000 kg材料所用的时间相同． kg材料所用的时间与B型机器人搬运800 （1）求A，B两种型号的机器人每小时分别搬运多少材料； （2）该公司计划采购A，B两种型号的机器人共20台，要求每小时搬运材料不 得少于2800 kg，则至少购进A型机器人多少台？ 24．某商场为方便消费者购物，准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯．如 图（十四）所示，已知原阶梯式自动扶梯AB长为10m，坡角∠ABD为30°；改造后的斜坡 式自动扶梯的坡角∠ACB为15°，请你计算 改造后的斜坡式自动扶梯AC的长度．（ 结果精确到0.1m．温馨提示：sin15°≈0.26， cos15°≈0.97，tan15°≈0.27 ） 25．如图（十五）所示，在四边形ABCD中，点O，E，F，G分别是AB，BC，CD，AD的中点， 连接OE，EF，FG，GO，GE． （1）证明：四边形OEFG是平行四边形； （2）将△OGE绕点O顺时针旋转得到△OMN，如图（十六）所示，连接GM，EN． EN 3①若OE＝ ，OG＝1，求 的值； GM ②试在四边形ABCD中添加一个条件，使GM，EN的长在旋转过程中始终相等． （不要求证明） 7826．如图（十七）所示，将二次函数y＝x2＋2x＋1的图象沿x轴翻折，然后向右平移1个单 位，再向上平移4个单位，得到二次函数y＝ax2＋bx＋c的图象．函数y＝x2＋2x＋1的图 象的顶点为点A．函数y＝ax2＋bx＋c的图象的顶点为点B，和x轴的交点为点C，D （点D位于点C的左侧）． （1）求函数y＝ax2＋bx＋c的解析式； （2）从点A，C，D三个点中任取两个点和点B构造三角形，求构造的三角形是等腰三 角形的概率； （3）若点M是线段BC上的动点，点N是△ABC三边上的动点，是否存在以AM为斜边的Rt 1△AMN，使△AMN的面积为△ABC面积的 ，若存在，求tan∠MAN的值；若不存在， 3请说明理由． 邵阳市2018年初中毕业学业考试参考答案及评分标准 数学选择题 题题题（本大 有10个小 ，每小 3分，共30分．在每小 题给 选项 一、 出的四个 中只有 项题是符合 目要求的） 一题号 12345678910 答案 CDDBBBDACA二、填空题（本大题有8个小题，每小题3分，共24分） 911．－2 12．答案不唯一．例如△EFC∽△AFD，△EAB∽△AFD，△EFC∽△EAB． 13．x＝0 14．40° 15．16000 16．x＝2 317． 18．4 三、解答题（本大题有8个小题，第19~25题每小题8分，第26题10分，共66分．解答应写 出必要的文字说明、演算步骤或证明过程） 19．（8分） 解：(－1 )2＋(π－3.14 )0－| －2| 22＝1＋1－(2－ )………………………………………………………………………5分 2＝2－2＋ ……………………………………………………………………7分 …………………………………………………………………………8分 2＝．20．（8分） 解：( a－2b )( a＋2b)－(a－2b)2＋8b2 ＝a2－(2b)2－(a2－4ab＋4b2)＋8b2 ＝a2－4b2－a2＋4ab－4b2＋8b2 ＝4ab． ……………………………………………………………………………6分 1将a＝－2，b＝ 代入得： 21原式＝4×(－2)× 2＝－4．… … … … … … … … … … … … … … … … … … … … … … … … … … … … … 8分 21．（8分） 证明：∵BC平分∠ABD，∴∠OBC＝∠DBC．……………………………………………2分 ∵OB＝OC，∴∠OBC＝∠OCB．……………………………………………………4分 ∴∠DBC＝∠OCB．∴OC∥BD．……………………………………………………6分 ∵BD⊥CD，∴OC⊥CD． 又∵点C为⊙O上一点， 10 ∴CD为⊙O的切线．…………………………………………………………………8分 22．（8分） 解：（1）服装项目的权数为10%，普通话项目对应扇形的圆心角为72°；……………2分 （2）众数为85，中位数为82.5；………………………………………………………4分 （3）李明的得分为80.5，张华的得分为78.5，应推荐李明参加比赛．……………8分 23．（8分） 解：（1）设A型机器人每小时搬运xkg材料，则B型机器人每小时搬运(x－30)kg材料， 1000 800 ＝依题意得： ．………………………………………………………2分 xx – 30 解得x＝150，经检验，x＝150是原方程的解． 所以A型机器人每小时搬运150kg材料，B型机器人每小时搬运120kg材料． 答：略．…………………………………………………………………………………4分 （2）设公司购进A型机器人y台，则购进B型机器人(20－y)台，依题意得： 150y＋120(20－y)≥2800．………………………………………6分 1解得y≥13 ．因为y为整数，所以公司至少购进A型机器人14台． 3答：略．…………………………………………………………………………………8分 24．（8分） 解：在Rt△ABD中，∠ABD＝30°， 1所以AD＝ AB＝5．………………………………………………………………………2分 2AD 在Rt△ACD中，sin∠ACD＝ ，AC AD 5所以AC＝ ＝≈19.2(m)． ∠sin ACD sin15° 答：略．……………………………………………………………………………………8 分11 25．（8分） 解：（1）连接AC， ∵点O，E，F，G分别是AB，BC，CD，AD的中点， 11∴OE∥AC，OE＝ AC，GF∥AC，GF＝ AC． 22∴OE∥GF，OE＝GF． ∴四边形OEFG是平行四边形．……………………………………………………3分 （2）①∵△OGE绕点O顺时针旋转得到△OMN， ∴OG＝OM，OE＝ON，∠GOM＝∠EON． OG OM ∴＝OE ON ．∴△OGM∽△OEN． EN OE 33．………………………………………………………6分 ∴＝＝＝GM OG ②答案不唯一，满足AC＝BD即可．……………………………………………8分 26．（10分） 1解：（1）将抛物线y＝x2＋2x＋1沿x轴翻折得到：y＝－x2－2x－1， 将抛物线y＝－x2－2x－1，向右平移1个单位得到：y＝－x2, 将抛物线y＝－x2向上平移4个单位得到：y＝－x2＋4． 所求函数y＝ax2＋bx＋c的解析式为y＝－x2＋4．………………………………2分 （2）从A，C，D三个点中任选两个点和点B构造的三角形有：△BAC，△BAD，△BCD． A，B，C，D的坐标分别为(－1，0)，(0，4)，(2，0)，(－2，0)， 17 55，CD＝4， 可求得AB＝ ，AC＝3，BC＝2 ，AD＝1，BD＝2 1只有△BCD为等腰三角形，所以构造的三角形是等腰三角形的概率P＝ ．…4分 311（3）S△ABC＝ AC·BO＝ ×3×4＝6． 22①当点N在边AC上时，点M在边BC上，在Rt△AMN中，MN⊥AC． 设点N的坐标为(m，0)，则AN＝m＋1，点M的横坐标为m． 由B(0，4)，C(2，0)易得线段BC的解析式为y＝－2x＋4，其中0≤x≤2， 所以点M的纵坐标为－2m＋4，则MN＝－2m＋4． 11S△AMN ＝ AN·MN＝ (m＋1)(－2m＋4) 221＝ S△ABC＝2． 3解得m1＝1，m2＝0． 当m＝1时，N点的坐标为(1，0)，M点的坐标为(1 ，2)，AN＝2，MN＝2． 12 MN AN 2tan∠MAN＝ ＝ ＝1．……………5分 2当m＝0时，N点的坐标为(0，0)，M点与点B重合，坐标为(0，4)，AN＝1，MN＝ 4． MN AN 4tan∠MAN＝ ＝ ＝4．………………………………………………………6分 1②当点N在BC上时，点M在BC上，Rt△AMN中，MN⊥AN， 1 1 11因为S△AMN＝ S△ABC，所以 AN·MN＝ × BC·AN， 323 2 1所以MN＝ BC＝ 52．33115因为S△ABC＝ BC·AN＝ ×2 ·AN＝6， 226所以AN＝ ．552MN AN 536所以tan∠MAN＝ ＝＝ ．…………8分 95③当点N在AB上时，点M在BC上，Rt△AMN中，MN⊥AN． 17 设AN＝t，则BN＝ –t， 6过点A作AG⊥BC于点G，由②得AG＝ ．57AB2 – AG2 在Rt△ABG中，BG＝ ＝．5易证△BNM∽△BGA， BN MN MN 17 7- t 所以 ＝BG AG ，即 ＝，65517 6- 6t 求得MN＝ ，71117 6- 6t ＝2， 所以S△AMN＝ AN·MN＝ t· 2272化简得3t2－3 t＋14＝0，△＝(3 17 17 ) －4×3×14＝－15＜0，此方程无解 ，13 所以此情况不存在． 综上所述，当点N在AC上，点M与点B重合时，tan∠MAN＝4； 当点N在AC上，点M不与点B重合时，tan∠MAN＝1； 5当点N在BC上时，tan∠MAN＝ ．…………………………10分 9注：解答题用其它方法解答参照给分． 14