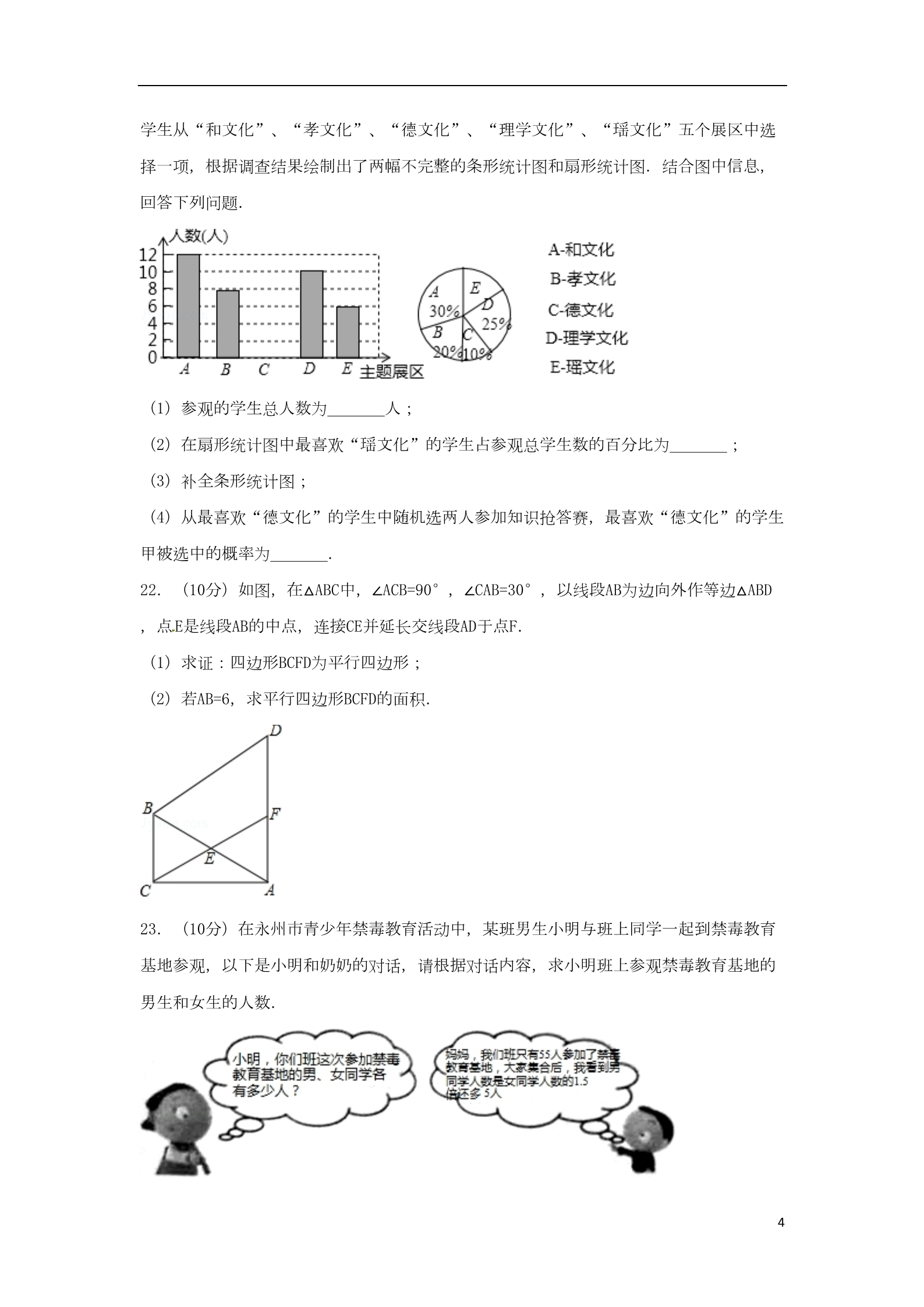
湖南省永州市2018年中考数学真题试题（含解析）

湖南省永州市2018年中考数学真题试题一、选择题（本大题共10个小题，每个小题只有一个正确选项，每小题4分，共40分 1．（4分）﹣2018的相反数是（　　） A．2018 B．﹣2018 C． D．﹣ 2．（4分）誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着500多方古今名家碑文，其中悬针篆文具有较高的历史意义和研究价值，下面四个悬针篆文文字明显不是轴对称图形的是（　　） A． B． C． D． 3．（4分）函数y= 中自变量x的取值范围是（　　） A．x≥3 B．x＜3 C．x≠3 D．x=3 4．（4分）如图几何体的主视图是（　　） A． B． C． D． 5．（4分）下列运算正确的是（　　） A．m2+2m3=3m5 B．m2•m3=m6 C．（﹣m）3=﹣m3 D．（mn）3=mn3 6．（4分）已知一组数据45，51，54，52，45，44，则这组数据的众数、中位数分别为（　　）A．45，48 B．44，45 C．45，51 D．52，53 7．（4分）下列命题是真命题的是（　　） A．对角线相等的四边形是矩形 B．对角线互相垂直的四边形是菱形 C．任意多边形的内角和为360° D．三角形的中位线平行于第三边，并且等于第三边的一半 8．（4分）如图，在△ABC中，点D是边AB上的一点，∠ADC=∠ACB，AD=2，BD=6，则边AC的长 1为（　　） A．2 B．4 C．6 D．8 9．（4分）在同一平面直角坐标系中，反比例函数y= （b≠0）与二次函数y=ax2+bx（a≠0 ）的图象大致是（　　） A． B． C． D． 10．（4分）甲从商贩A处购买了若干斤西瓜，又从商贩B处购买了若干斤西瓜．A、B两处所购买的西瓜重量之比为3：2，然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙，结果发现他赔钱了，这是因为（　　） A．商贩A的单价大于商贩B的单价 B．商贩A的单价等于商贩B的单价 C．商版A的单价小于商贩B的单价 D．赔钱与商贩A、商贩B的单价无关　二、填空题（本大题共8个小题，每小题4分，共32分） 11．（4分）截止2017年年底，我国60岁以上老龄人口达2.4亿，占总人口比重达17.3%．将 2.4亿用科学记数法表示为　　．　． 12．（4分）因式分解：x2﹣1=　 13．（4分）一副透明的三角板，如图叠放，直角三角板的斜边AB、CE相交于点D，则∠BDC =　． 214．（4分）化简：（1+ ）÷ =　　． 15．（4分）在一个不透明的盒子中装有n个球，它们除了颜色之外其它都没有区别，其中含有3个红球，每次摸球前，将盒中所有的球摇匀，然后随机摸出一个球，记下颜色后再放回盒中．通过大量重复试验，发现摸到红球的频率稳定在0.03，那么可以推算出n的值大约是　 16．（4分）如图，在平面直角坐标系中，已知点A（1，1），以点O为旋转中心，将点A逆时针旋转到点B的位置，则的长为　．　． 17．（4分）对于任意大于0的实数x、y，满足：log2（x•y）=log2x+log2y，若log22=1，则 log216=　． 18．（4分）现有A、B两个大型储油罐，它们相距2km，计划修建一条笔直的输油管道，使得A、B两个储油罐到输油管道所在直线的距离都为0.5km，输油管道所在直线符合上述要求的设计方案有　　种．　三、解答题（本大题共8个小题，解答题要求写出证明步骤或解答过程） 19．（8分）计算：2﹣1 ﹣sin60°+|1﹣ |． 20．（8分）解不等式组，并把解集在数轴上表示出来． 21．（8分）永州植物园“清风园”共设11个主题展区．为推进校园文化建设，某校九年级（1）班组织部分学生到“清风园”参观后，开展“我最喜欢的主题展区”投票调查．要求 3学生从“和文化”、“孝文化”、“德文化”、“理学文化”、“瑶文化”五个展区中选择一项，根据调查结果绘制出了两幅不完整的条形统计图和扇形统计图．结合图中信息，回答下列问题．（1）参观的学生总人数为　　人；（2）在扇形统计图中最喜欢“瑶文化”的学生占参观总学生数的百分比为　（3）补全条形统计图；　；（4）从最喜欢“德文化”的学生中随机选两人参加知识抢答赛，最喜欢“德文化”的学生甲被选中的概率为　． 22．（10分）如图，在△ABC中，∠ACB=90°，∠CAB=30°，以线段AB为边向外作等边△ABD ，点E是线段AB的中点，连接CE并延长交线段AD于点F．（1）求证：四边形BCFD为平行四边形；（2）若AB=6，求平行四边形BCFD的面积． 23．（10分）在永州市青少年禁毒教育活动中，某班男生小明与班上同学一起到禁毒教育基地参观，以下是小明和奶奶的对话，请根据对话内容，求小明班上参观禁毒教育基地的男生和女生的人数． 424．（10分）如图，线段AB为⊙O的直径，点C，E在⊙O上， = ，CD⊥AB，垂足为点D，连接BE，弦BE与线段CD相交于点F．（1）求证：CF=BF；（2）若cos∠ABE= ，在AB的延长线上取一点M，使BM=4，⊙O的半径为6．求证：直线CM是 ⊙O的切线． 25．（12分）如图1，抛物线的顶点A的坐标为（1，4），抛物线与x轴相交于B、C两点，与 y轴交于点E（0，3）．（1）求抛物线的表达式；（2）已知点F（0，﹣3），在抛物线的对称轴上是否存在一点G，使得EG+FG最小，如果存在，求出点G的坐标：如果不存在，请说明理由．（3）如图2，连接AB，若点P是线段OE上的一动点，过点P作线段AB的垂线，分别与线段AB 、抛物线相交于点M、N（点M、N都在抛物线对称轴的右侧），当MN最大时，求△PON的面积．26．（12分）如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，C D是边AB上的高，CD交GH于点I．若CI=4，HI=3，AD= ．矩形DFGI恰好为正方形． 5（1）求正方形DFGI的边长；（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP 上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长．　6参考答案与试题解析一、选择题（本大题共10个小题，每个小题只有一个正确选项，每小题4分，共40分 1．（4分）﹣2018的相反数是（　　） A．2018 B．﹣2018 C． D．﹣ 【分析】只有符号不同的两个数叫做互为相反数．【解答】解：﹣2018的相反数是2018．故选：A．【点评】本题主要考查的是相反数的定义，掌握相反数的定义是解题的关键．　2．（4分）誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着500多方古今名家碑文，其中悬针篆文具有较高的历史意义和研究价值，下面四个悬针篆文文字明显不是轴对称图形的是（　　） A． B． C． D．【分析】根据轴对称图形的概念进行判断即可．【解答】解：A、是轴对称图形，故此选项错误； B、是轴对称图形，故此选项错误； C、不是轴对称图形，故此选项正确； D、是轴对称图形，故此选项错误；故选：C．【点评】本题考查的是轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．　3．（4分）函数y= 中自变量x的取值范围是（　　） A．x≥3 B．x＜3 C．x≠3 D．x=3 【分析】根据分式的意义，分母不等于0，可以求出x的范围．【解答】解：根据题意得：x﹣3≠0，解得：x≠3． 7故选：C．【点评】考查了函数自变量的范围，注意：函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．　4．（4分）如图几何体的主视图是（　　） A． B． C． D．【分析】依据从该几何体的正面看到的图形，即可得到主视图．【解答】解：由图可得，几何体的主视图是：故选：B．【点评】本题主要考查了三视图，解题时注意：视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上．　5．（4分）下列运算正确的是（　　） A．m2+2m3=3m5 B．m2•m3=m6 C．（﹣m）3=﹣m3 D．（mn）3=mn3 【分析】根据合并同类项法则、同底数幂的乘法、幂的乘方与积的乘方逐一计算可得．【解答】解：A、m2与2m3不是同类项，不能合并，此选项错误； B、m2•m3=m5，此选项错误； C、（﹣m）3=﹣m3，此选项正确； D、（mn）3=m3n3，此选项错误；故选：C．【点评】本题主要考查整式的运算，解题的关键是掌握合并同类项法则、同底数幂的乘法 8、幂的乘方与积的乘方．　6．（4分）已知一组数据45，51，54，52，45，44，则这组数据的众数、中位数分别为（　　）A．45，48 B．44，45 C．45，51 D．52，53 【分析】先把原数据按由小到大排列，然后根据众数、中位数的定义求解．【解答】解：数据从小到大排列为：44，45，45，51，52，54，所以这组数据的众数为45，中位数为（45+51）=48．故选：A．【点评】本题考查了众数：一组数据中出现次数最多的数据叫做众数．也考查了中位数．　7．（4分）下列命题是真命题的是（　　） A．对角线相等的四边形是矩形 B．对角线互相垂直的四边形是菱形 C．任意多边形的内角和为360° D．三角形的中位线平行于第三边，并且等于第三边的一半【分析】根据矩形的判定方法对A进行判断；根据菱形的判定方法对B进行判断；根据多边形的内角和对C进行判断；根据三角形中位线性质对D进行判断．【解答】解：A、对角线相等的平行四边形是矩形，所以A选项为假命题； B、对角线互相垂直的平行四边形是菱形，所以B选项为假命题； C、任意多边形的外角和为360°，所以C选项为假命题； D、三角形的中位线平行于第三边且等于第三边的一半，所以D选项为真命题．故选：D．【点评】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成 “如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．　8．（4分）如图，在△ABC中，点D是边AB上的一点，∠ADC=∠ACB，AD=2，BD=6，则边AC的长为（　　） 9A．2 B．4 C．6 D．8 【分析】只要证明△ADC∽△ACB，可得 = ，即AC2=AD•AB，由此即可解决问题；【解答】解：∵∠A=∠A，∠ADC=∠ACB， ∴△ADC∽△ACB， ∴ = ，∴AC2=AD•AB=2×8=16， ∵AC＞0， ∴AC=4，故选：B．【点评】本题考查相似三角形的判定和性质、解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．　9．（4分）在同一平面直角坐标系中，反比例函数y= （b≠0）与二次函数y=ax2+bx（a≠0 ）的图象大致是（　　） A． B． C． D．【分析】直接利用二次函数图象经过的象限得出a，b的值取值范围，进而利用反比例函数的性质得出答案．【解答】解：A、抛物线y=ax2+bx开口方向向上，则a＞0，对称轴位于y轴的右侧，则a、b 异号，即b＜0．所以反比例函数y= 的图象位于第二、四象限，故本选项错误； B、抛物线y=ax2+bx开口方向向上，则a＞0，对称轴位于y轴的左侧，则a、b同号，即b＞0 ．所以反比例函数y= 的图象位于第一、三象限，故本选项错误； C、抛物线y=ax2+bx开口方向向下，则a＜0，对称轴位于y轴的右侧，则a、b异号，即b＞0 10 ．所以反比例函数y= 的图象位于第一、三象限，故本选项错误； D、抛物线y=ax2+bx开口方向向下，则a＜0，对称轴位于y轴的右侧，则a、b异号，即b＞0 ．所以反比例函数y= 的图象位于第一、三象限，故本选项正确；故选：D．【点评】此题主要考查了反比例函数的图象，以及二次函数的图象，要熟练掌握二次函数，反比例函数中系数与图象位置之间关系．　10．（4分）甲从商贩A处购买了若干斤西瓜，又从商贩B处购买了若干斤西瓜．A、B两处所购买的西瓜重量之比为3：2，然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙，结果发现他赔钱了，这是因为（　　） A．商贩A的单价大于商贩B的单价 B．商贩A的单价等于商贩B的单价 C．商版A的单价小于商贩B的单价 D．赔钱与商贩A、商贩B的单价无关【分析】本题考查一元一次不等式组的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解．【解答】解：利润=总售价﹣总成本= ×5﹣（3a+2b）=0.5b﹣0.5a，赔钱了说明利润＜ 0∴0.5b﹣0.5a＜0， ∴a＞b．故选：A．【点评】此题考查一元一次不等式组的应用，解决本题的关键是读懂题意，找到符合题意的不等关系式．　二、填空题（本大题共8个小题，每小题4分，共32分） 11．（4分）截止2017年年底，我国60岁以上老龄人口达2.4亿，占总人口比重达17.3%．将 2.4亿用科学记数法表示为　2.4×108　．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原 11 数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：2.4亿=2.4×108．故答案为：2.4×108 【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤ |a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　12．（4分）因式分解：x2﹣1=　（x+1）（x﹣1）　．【分析】方程利用平方差公式分解即可．【解答】解：原式=（x+1）（x﹣1）．故答案为：（x+1）（x﹣1）．【点评】此题考查了因式分解﹣运用公式法，熟练掌握平方差公式是解本题的关键．　13．（4分）一副透明的三角板，如图叠放，直角三角板的斜边AB、CE相交于点D，则∠BDC =　75°　．【分析】根据三角板的性质以及三角形内角和定理计算即可；【解答】解：∵∠CEA=60°，∠BAE=45°， ∴∠ADE=180°﹣∠CEA﹣∠BAE=75°， ∴∠BDC=∠ADE=75°，故答案为75°．【点评】本题考查三角板的性质，三角形内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考基础题．　14．（4分）化简：（1+ ）÷ =　　．【分析】根据分式的加法和除法可以解答本题． 12 【解答】解：（1+ ）÷ ===，故答案为：．【点评】本题考查分式的混合运算，解答本题的关键是明确分式的混合运算的计算方法．　15．（4分）在一个不透明的盒子中装有n个球，它们除了颜色之外其它都没有区别，其中含有3个红球，每次摸球前，将盒中所有的球摇匀，然后随机摸出一个球，记下颜色后再放回盒中．通过大量重复试验，发现摸到红球的频率稳定在0.03，那么可以推算出n的值大约是　100　．【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，列出方程求解．【解答】解：由题意可得， =0.03，解得，n=100．故估计n大约是100．故答案为：100．【点评】此题主要考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：概率=所求情况数与总情况数之比．　16．（4分）如图，在平面直角坐标系中，已知点A（1，1），以点O为旋转中心，将点A逆时针旋转到点B的位置，则的长为　　． 13 【分析】由点A（1，1），可得OA= =，点A在第一象限的角平分线上，那么∠AO B=45°，再根据弧长公式计算即可．【解答】解：∵点A（1，1）， ∴OA= =，点A在第一象限的角平分线上， ∵以点O为旋转中心，将点A逆时针旋转到点B的位置， ∴∠AOB=45°， ∴的长为故答案为【点评】本题考查了弧长公式：l= =．．（弧长为l，圆心角度数为n，圆的半径为R），也考查了坐标与图形变化﹣旋转，求出OA= 以及∠AOB=45°是解题的关键．　17．（4分）对于任意大于0的实数x、y，满足：log2（x•y）=log2x+log2y，若log22=1，则 log216=　4　．【分析】利用log2（x•y）=log2x+log2y得到log216=log22+log22+log22+log22，然后根据log 22=1进行计算．【解答】解：log216=log2（2•2•2•2）=log22+log22+log22+log22=1+1+1+1=4．故答案为4．【点评】本题考查了规律型：认真观察、仔细思考，善用联想是解决这类问题的方法．　18．（4分）现有A、B两个大型储油罐，它们相距2km，计划修建一条笔直的输油管道，使得A、B两个储油罐到输油管道所在直线的距离都为0.5km，输油管道所在直线符合上述要求的设计方案有　4　种．【分析】根据点A、B的可以在直线的两侧或异侧两种情形讨论即可；【解答】解：输油管道所在直线符合上述要求的设计方案有4种，如图所示； 14 故答案为4．【点评】本题考查整体﹣应用与设计，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．　三、解答题（本大题共8个小题，解答题要求写出证明步骤或解答过程） 19．（8分）计算：2﹣1 ﹣sin60°+|1﹣ |．【分析】原式利用负整数指数幂法则，特殊角的三角函数值，以及绝对值的代数意义计算即可求出值．【解答】解：原式= ﹣× +2=1．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．　20．（8分）解不等式组，并把解集在数轴上表示出来．【分析】分别解不等式组的两个不等式，即可得到其公共部分，依据解集即可在数轴上表示出来．【解答】解：，解不等式①，可得 x＜3，解不等式②，可得 x＞﹣1， ∴不等式组的解集为﹣1＜x＜3，在数轴上表示出来为： 15 【点评】本题主要考查了解一元一次不等式组，解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．　21．（8分）永州植物园“清风园”共设11个主题展区．为推进校园文化建设，某校九年级（1）班组织部分学生到“清风园”参观后，开展“我最喜欢的主题展区”投票调查．要求学生从“和文化”、“孝文化”、“德文化”、“理学文化”、“瑶文化”五个展区中选择一项，根据调查结果绘制出了两幅不完整的条形统计图和扇形统计图．结合图中信息，回答下列问题．（1）参观的学生总人数为　40　人；（2）在扇形统计图中最喜欢“瑶文化”的学生占参观总学生数的百分比为　15%　；（3）补全条形统计图；（4）从最喜欢“德文化”的学生中随机选两人参加知识抢答赛，最喜欢“德文化”的学生甲被选中的概率为　．【分析】（1）依据最喜欢“和文化”的学生数以及百分比，即可得到参观的学生总人数；（2）依据最喜欢“瑶文化”的学生数，即可得到其占参观总学生数的百分比；（3）依据“德文化”的学生数为40﹣12﹣8﹣10﹣6=4，即可补全条形统计图；（4）设最喜欢“德文化”的4个学生分别为甲乙丙丁，画树状图可得最喜欢“德文化”的学生甲被选中的概率．【解答】解：（1）参观的学生总人数为12÷30%=40（人）；（2）喜欢“瑶文化”的学生占参观总学生数的百分比为 ×100%=15%；（3）“德文化”的学生数为40﹣12﹣8﹣10﹣6=4，条形统计图如下： 16 （4）设最喜欢“德文化”的4个学生分别为甲乙丙丁，画树状图得： ∵共有12种等可能的结果，甲同学被选中的有6种情况， ∴甲同学被选中的概率是： = 故答案为：40；15%；．．【点评】此题考查了条形统计图和扇形统计图，树状图法与列表法求概率．用到的知识点为：概率=所求情况数与总情况数之比．　22．（10分）如图，在△ABC中，∠ACB=90°，∠CAB=30°，以线段AB为边向外作等边△ABD ，点E是线段AB的中点，连接CE并延长交线段AD于点F．（1）求证：四边形BCFD为平行四边形；（2）若AB=6，求平行四边形BCFD的面积．【分析】（1）在Rt△ABC中，E为AB的中点，则CE= AB，BE= AB，得到∠BCE=∠EBC=60°．由△AEF≌△BEC，得∠AFE=∠BCE=60°．又∠D=60°，得∠AFE=∠D=60度．所以FC∥BD，又因为 ∠BAD=∠ABC=60°，所以AD∥BC，即FD∥BC，则四边形BCFD是平行四边形．（2）在Rt△ABC中，求出BC，AC即可解决问题； 17 【解答】（1）证明：在△ABC中，∠ACB=90°，∠CAB=30°， ∴∠ABC=60°．在等边△ABD中，∠BAD=60°， ∴∠BAD=∠ABC=60°． ∵E为AB的中点， ∴AE=BE．又∵∠AEF=∠BEC， ∴△AEF≌△BEC．在△ABC中，∠ACB=90°，E为AB的中点， ∴CE= AB，BE= AB． ∴CE=AE， ∴∠EAC=∠ECA=30°， ∴∠BCE=∠EBC=60°．又∵△AEF≌△BEC， ∴∠AFE=∠BCE=60°．又∵∠D=60°， ∴∠AFE=∠D=60°． ∴FC∥BD．又∵∠BAD=∠ABC=60°， ∴AD∥BC，即FD∥BC． ∴四边形BCFD是平行四边形．（2）解：在Rt△ABC中，∵∠BAC=30°，AB=6， ∴BC= AB=3，AC= BC=3 ∴S平行四边形BCFD=3× =9 ，．18 【点评】本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直角三角形、勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．　23．（10分）在永州市青少年禁毒教育活动中，某班男生小明与班上同学一起到禁毒教育基地参观，以下是小明和奶奶的对话，请根据对话内容，求小明班上参观禁毒教育基地的男生和女生的人数．【分析】设小明班上参观禁毒教育基地的男生人数为x人，女生人数为y人，根据“男生人数+女生人数=55、男生人数=1.5×女生人数+5”列出方程组并解答．【解答】解：设小明班上参观禁毒教育基地的男生人数为x人，女生人数为y人，依题意得：，解得，答：小明班上参观禁毒教育基地的男生人数为35人，女生人数为20人．【点评】考查了二元一次方程组的应用．分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．　24．（10分）如图，线段AB为⊙O的直径，点C，E在⊙O上， = ，CD⊥AB，垂足为点D，连接BE，弦BE与线段CD相交于点F．（1）求证：CF=BF； 19 （2）若cos∠ABE= ，在AB的延长线上取一点M，使BM=4，⊙O的半径为6．求证：直线CM是 ⊙O的切线．【分析】（1）延长CD交⊙O于G，如图，利用垂径定理得到 = ，则可证明 = ，然后根据圆周角定理得∠CBE=∠GCB，从而得到CF=BF；（2）连接OC交BE于H，如图，先利用垂径定理得到OC⊥BE，再在Rt△OBH中利用解直角三角形得到BH= ，OH= ，接着证明△OHB∽△OCM得到∠OCM=∠OHB=90°，然后根据切线的判定定理得到结论．【解答】证明：（1）延长CD交⊙O于G，如图， ∵CD⊥AB， ∴ = ∵ = ∴ = ，，，∴∠CBE=∠GCB， ∴CF=BF；（2）连接OC交BE于H，如图， ∵ = ，∴OC⊥BE，在Rt△OBH中，cos∠OBH= = ，∴BH= ×6= ∴OH= ，=，20 ∵ = =， = ∴ = = ，，而∠HOB=∠COM， ∴△OHB∽△OCM， ∴∠OCM=∠OHB=90°， ∴OC⊥CM， ∴直线CM是⊙O的切线．【点评】本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了垂径定理、圆周角定理和解直角三角形．　25．（12分）如图1，抛物线的顶点A的坐标为（1，4），抛物线与x轴相交于B、C两点，与 y轴交于点E（0，3）．（1）求抛物线的表达式；（2）已知点F（0，﹣3），在抛物线的对称轴上是否存在一点G，使得EG+FG最小，如果存在，求出点G的坐标：如果不存在，请说明理由．（3）如图2，连接AB，若点P是线段OE上的一动点，过点P作线段AB的垂线，分别与线段AB 、抛物线相交于点M、N（点M、N都在抛物线对称轴的右侧），当MN最大时，求△PON的面积．21 【分析】（1）根据顶点式可求得抛物线的表达式；（2）根据轴对称的最短路径问题，作E关于对称轴的对称点E’，连接E’F交对称轴于G，此时EG+FG的值最小，先求E’F的解析式，它与对称轴的交点就是所求的点G；（3）如图2，先利用待定系数法求AB的解析式为：y=﹣2x+6，设N（m，﹣m2+2m+3），则Q （m，﹣2m+6），（0≤m≤3），表示NQ=﹣m2+4m﹣3，证明△QMN∽△ADB，列比例式可得MN的表达式，根据配方法可得当m=2时，MN有最大值，证明△NGP∽△ADB，同理得PG的长，从而得OP的长，根据三角形的面积公式可得结论，并将m=2代入计算即可．【解答】解：（1）设抛物线的表达式为：y=a（x﹣1）2+4，把（0，3）代入得：3=a（0﹣1）2+4， a=﹣1， ∴抛物线的表达式为：y=﹣（x﹣1）2+4=﹣x2+2x+3；（2）存在，如图1，作E关于对称轴的对称点E’，连接E’F交对称轴于G，此时EG+FG的值最小， ∵E（0，3）， ∴E’（2，3），易得E’F的解析式为：y=3x﹣3，当x=1时，y=3×1﹣3=0， ∴G（1，0）（3）如图2，∵A（1，4），B（3，0），易得AB的解析式为：y=﹣2x+6，设N（m，﹣m2+2m+3），则Q（m，﹣2m+6），（0≤m≤3）， ∴NQ=（﹣m2+2m+3）﹣（﹣2m+6）=﹣m2+4m﹣3， ∵AD∥NH， ∴∠DAB=∠NQM， 22 ∵∠ADB=∠QMN=90°， ∴△QMN∽△ADB， ∴，∴，∴MN=﹣ ∵﹣ （m﹣2）2+ ＜0，，∴当m=2时，MN有最大值；过N作NG⊥y轴于G， ∵∠GPN=∠ABD，∠NGP=∠ADB=90°， ∴△NGP∽△ADB， ∴= = ，∴PG= NG= m， ∴OP=OG﹣PG=﹣m2+2m+3﹣ m=﹣m2+ m+3， ∴S△PON= OP•GN= （﹣m2+ m+3）•m，当m=2时，S△PON= ×2（﹣4+3+3）=2． 23 【点评】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、一次函数的解析式、相似三角形的性质和判定、三角形的面积、轴对称的最短路径问题，根据比例式列出关于m的方程是解题答问题（3）的关键．　26．（12分）如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，C D是边AB上的高，CD交GH于点I．若CI=4，HI=3，AD= ．矩形DFGI恰好为正方形．（1）求正方形DFGI的边长；（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP 上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长．【分析】（1）由HI∥AD，得到 = ，求出AD即可解决问题；（2）如图2中，设等G落在PC时对应的点为G′，点F的对应的点为F′．求出IG′和BD的长比较即可判定；（3）如图3中，如图将△DMI′绕点D逆时针旋转90°得到△DF′R，此时N、F′、R共线．想办法证明MN=MI′+NF′，即可解决问题；【解答】解：（1）如图1中， 24 ∵HI∥AD， ∴ = ，∴ = ，∴AD=6， ∴ID=CD﹣CI=2， ∴正方形的边长为2．（2）如图2中，设等G落在PC时对应的点为G′，点F的对应的点为F′． ∵CA=CP，CD⊥PA， ∴∠ACD=∠PCD，∠A=∠P， ∵HG′∥PA， ∴∠CHG′=∠A，∠CG′H=∠P， ∴∠CHG′=∠CG′H， ∴CH=CG′， ∴IH=IG′=DF′=3， ∵IG∥DB， ∴ = ∴ = ，，25 ∴DB=3， ∴DB=DF′=3， ∴点B与点F′重合， ∴移动后的矩形与△CBP重叠部分是△BGG′， ∴移动后的矩形与△CBP重叠部分的形状是三角形．（3）如图3中，如图将△DMI′绕点D逆时针旋转90°得到△DF′R，此时N、F′、R共线． ∵∠MDN=∠NDF+∠MDI′=∠NDF′+∠DF′R=∠NDR=45°， ∵DN=DN，DM=DR， ∴△NDM≌△NDR， ∴MN=NR=NF′+RF′=NF′+MI′， ∴△MNG′的周长=MN+MG′+NG′=MG′+MI′+NG′+F′R=2I′G′=4．【点评】本题考查四边形综合题、矩形的性质、正方形的性质、平行线等分线段定理、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用旋转法添加辅助线，构造全等三角形解决问题，属于中考压轴题．　26