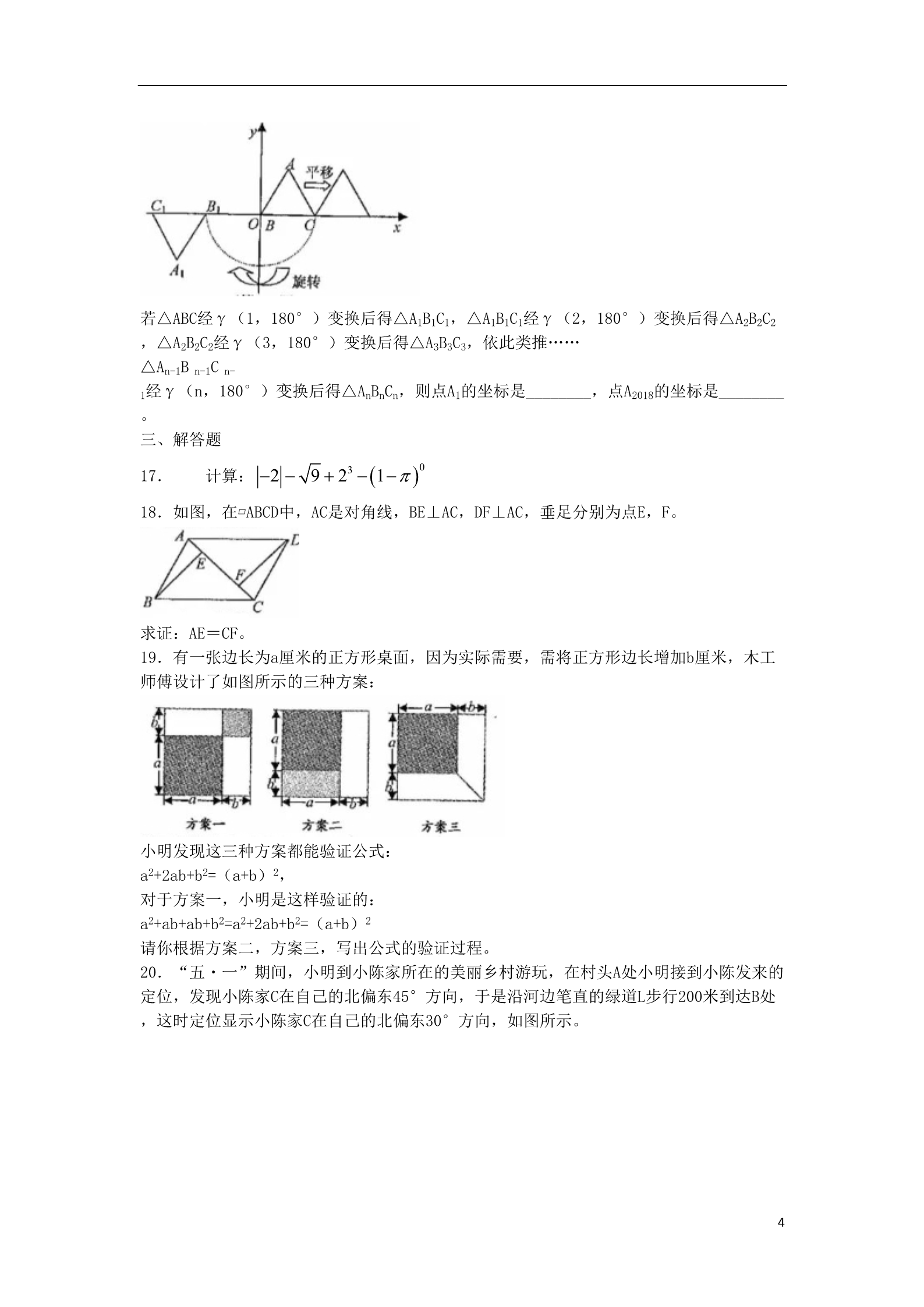
浙江省衢州市2018年中考数学真题试题（含扫描答案）

浙江省衢州市2018年中考数学真题试题一、选择题 1．-3的相反数是（）1313A．3 B．-3 C． D． 2．如图，直线a，b效直线c所截，那么∠1的同位角是（▲） A．∠2 B．∠3 C．∠4 D．∠5 3．根据衢州市统计局发布的统计数据显示，衢州市2017年全市生产总值为138000000000元，按可比价格计算，比上年增长7.3%，数据138000000000元用科学记数法表示为（▲） A．1.38×1010元 B．1.38×1011元 C．1.38×1012元 D．0.138×1012元 4．由五个大小相同的正方体组成的几何体如图所示，那么它的主视图是（▲） A． B． C． D． 5．如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（▲） 1A．75° B．70° C．65° D．35° 6．某班共有42名同学，其中有2名同学习惯用左手写字，其余同学都习惯用右手写字，老师随机请1名同学解答问题，习惯用左手写字的同学被选中的概率是（ A．0 ）1B． 21 1C． 42 D．1 7．不等式3x＋2≥5的解集是（▲） A．x≥1 7B． x  3C．x≤1 D．x≤－1 8．如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE=32°，则∠GHC等于（▲） A．112° B．110° C．108° D．106° 9．如图，AB是圆锥的母线，BC为底面直径，已知BC=6cm，圆锥的面积为15πcm2，则sin∠ ABC的值为（）3A． 43B． 54C． 5253D． 10．如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2c m，则OF的长度是（ A．3cm ）B． C．2.5cm D． cm 二、填空题 6cm 511．分解因式： x2 9  ________· 12．数据5，5，4，2，3，7，6的中位数是________· 13．如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，BF＝CE，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是________________（只需写一个，不添加辅助线） 14．星期天，小明上午8：00从家里出发，骑车到图书馆去借书，再骑车回到家，他离家的距离y（千米）与时间t（分钟）的关系如图所示，则上午8：45小明离家的距离是________ 千米。 k15．如图，点A，B是反比例函数 y  x  0 图象上的两点，过点A，B分别作AC⊥x轴于 x点C，BD⊥x于点D，连接OA，BC，已知点C（2，0），BD＝2，S△BCD＝3，则S△AOC＝________ 。16．定义；在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫做图形的γ（a，θ）变换。如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△ A1B1C1就是△ABC经γ（1，180°）变换后所得的图形． 3若△ABC经γ（1，180°）变换后得△A1B1C1，△A1B1C1经γ（2，180°）变换后得△A2B2C2 ，△A2B2C2经γ（3，180°）变换后得△A3B3C3，依此类推…… △An-1B n-1C n- 1经γ（n，180°）变换后得△AnBnCn，则点A1的坐标是________，点A2018的坐标是________ 。三、解答题 017．计算： 2  9  23  1 18．如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F。求证：AE＝CF。 19．有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：小明发现这三种方案都能验证公式： a2+2ab+b2=（a+b）2，对于方案一，小明是这样验证的： a2+ab+ab+b2=a2+2ab+b2=（a+b）2 请你根据方案二，方案三，写出公式的验证过程。 20．“五・一”期间，小明到小陈家所在的美丽乡村游玩，在村头A处小明接到小陈发来的定位，发现小陈家C在自己的北偏东45°方向，于是沿河边笔直的绿道L步行200米到达B处，这时定位显示小陈家C在自己的北偏东30°方向，如图所示。 4根据以上信息和下面的对话，请你帮小明算一算他还需沿绿道继续直走多少米才到达桥头D 处（精确到1米）。备用数据 ≈1.414， ≈1.732） 2321．为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”“文明交通”、“关爱老人”、“义务植树”“社区服务”等五项，活动期间，随机抽取了部分学生对志者服务情况进行调查．结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如所示不完整的折线统计图和扇形统计图。（1）被随机抽取的学生共有多少名？（2）在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；（3）该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？ 22．如图，已知AB为⊙O直径，AC是⊙O的切线，连接BC交⊙O于点F，取弧BF的中点D，连接 AD交BC于点E，过点E作EF⊥AB于H。 5（1）求证：△HBE∽△ABC；（2）若CF＝4，BF＝5，求AC和EH的长。 23．某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合，如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系。（1）求水柱所在抛物线（第一象限部分）的函数表达式；（2）王师傅在水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？（3）经检修评估，游乐园决定对喷水设施做如下设计改进；在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后水热水柱的最大高度。 24．如图，Rt△OAB的直角边OA在x轴上，顶点B的坐标为（6，8），直线CD交AB于点D（6， 3），交x轴于点C（12，0）。（1）求直线CD的函数表达式；（2）动点P在x轴上从点（－10，0）出发，以每秒1个单位的速度向x轴正方向运动，过点P 作直线L垂直于x轴，设运动时间为t。 ①点P在运动过程中，是否存在某个位置，使得∠PDA=∠B，若存在，请求出点P的坐标；若不存在，请说明理由； ②请探索当t为何值时，在直线L上存在点M，在直线CD上存在点Q，使得以OB为一边，O，B ，M，Q为顶点的四边形为菱形，并求出此时t的值。 678910