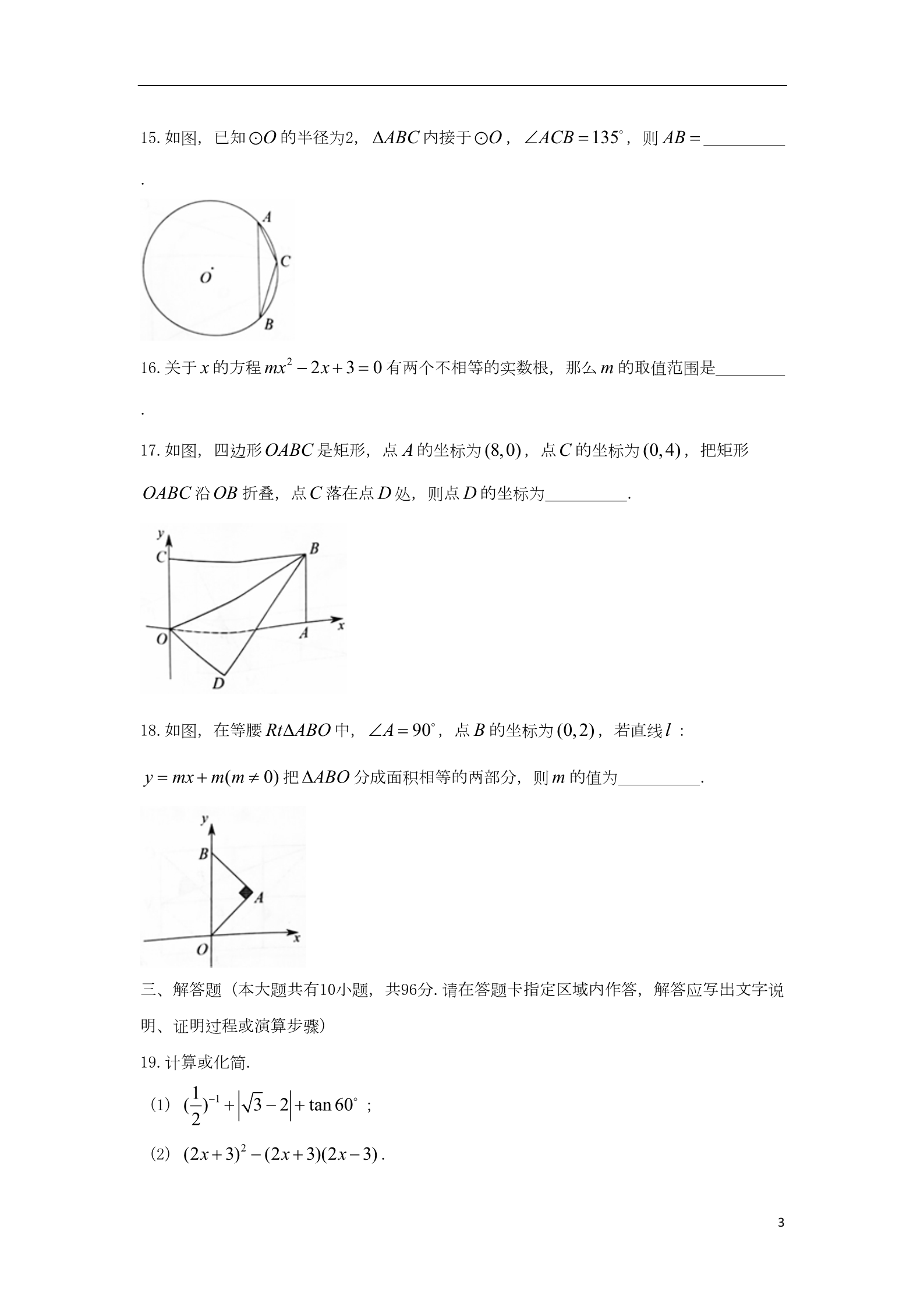
江苏省扬州市2018年中考数学真题试题（含答案）

江苏省扬州市2018年中考数学真题试题一、选择题： 1．  5的倒数是（）11A． B． C．5 D．  5 552．使 x 3 有意义的 x的取值范围是（）A． x  3 B． x  3 C． x  3 D． x  3 3.如图所示的几何体的主视图是（）A． B． C． D． 4.下列说法正确的是（）A．一组数据2，2，3，4，这组数据的中位数是2 B．了解一批灯泡的使用寿命的情况，适合抽样调查 C．小明的三次数学成绩是126分，130分，136分，则小明这三次成绩的平均数是131分 D．某日最高气温是 7 C ，最低气温是 2 C ，则该日气温的极差是5 C 35.已知点 A(x1,3) 、 B(x2 ,6) 都在反比例函数 y  的图象上，则下列关系式一定正确的 x是（）A． x1  x2  0 B． x1  0  x2 C． x2  x1  0 D． x2  0  x1 6.在平面直角坐标系的第二象限内有一点 M，点 M到x轴的距离为3，到 y轴的距离为4 ，则点 M的坐标是（）A． (3,4) B． (4,3) C． (4,3) CE 平分 ACD D． (3,4) 7.在 RtABC 中， ACB  90 ，CD  AB 于D，交 AB 于 E ，则下 1列结论一定成立的是（）A． BC  EC B． EC  BE C． BC  BE D． AE  EC CD 与 BE 8.如图，点 A在线段 BD 上，在 BD 的同侧作等腰 RtABC 和等腰 RtADE ，、AE 分别交于点 .对于下列结论： P 、 M ①BAE  CAD ；② MPMD  MAME ；③ 2CB2  CPCM .其中正确的是（）A．①②③ B．① C．①② D．②③ 二、填空题（本大题共有10小题，每小题3分，共30分.不需写出解答过程，请把答案直接填写在答题卡相应位置上） 9.在人体血液中，红细胞直径约为 0.00077cm ，数据0.00077用科学记数法表示为．10.因式分解：18 2×2  11.有4根细木棒，长度分别为2cm、3cm、4cm、5cm，从中任选3根，恰好能搭成一个三角形的概率是 12.若 m 是方程 2×2 3x 1 0的一个根，则 6m2 9m  2015的值为 13.用半径为10cm，圆心角为120 的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆．．．半径为 cm ．3x 1 5x 14.不等式组的解集为． x 1  2  2 215.如图，已知 O 的半径为2， ABC 内接于 O ， ACB 135 ，则 AB  ．16.关于 x的方程 mx2  2x  3  0 有两个不相等的实数根，那么 m 的取值范围是．17.如图，四边形OABC 是矩形，点 A的坐标为 (8,0)，点的坐标为 C的坐标为 (0,4) ，把矩形 OABC 沿OB 折叠，点落在点处，则点 CDD．18.如图，在等腰 RtABO 中， A  90 ，点 B 的坐标为 (0,2) ，若直线l ： y  mx  m(m  0) 把 ABO 分成面积相等的两部分，则 m 的值为．三、解答题（本大题共有10小题，共96分.请在答题卡指定区域内作答，解答应写出文字说明、证明过程或演算步骤） 19.计算或化简. 1（1） ( )1  3  2  tan 60 ；2（2） (2x  3)2  (2x  3)(2x 3) .320. 对于任意实数 a、b，定义关于“  ”的一种运算如下： a b  2a  b .例如 3 4  23 4 10 .（1）求 2(5) 的值；（2）若 x (y)  2 ，且 2y  x  1，求 x  y 的值. 21.江苏省第十九届运动会将于2018年9月在扬州举行开幕式，某校为了了解学生“最喜爱的省运会项目”的情况，随机抽取了部分学生进行问卷调查，规定每人从“篮球”、“羽毛球”、 “自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个，并将调查结果绘制成如下两幅不完整的统计图表. 最喜爱的省运会项目的人数调查统计表最喜爱的项目篮球人数 20 9羽毛球自行车游泳 10 a其他 b合计根据以上信息，请回答下列问题：（1）这次调查的样本容量是，a  b  ；（2）扇形统计图中“自行车”对应的扇形的圆心角为度；（3）若该校有1200名学生，估计该校最喜爱的省运会项目是篮球的学生人数. 22.4张相同的卡片上分别写有数字-1、-3、4、6，将卡片的背面朝上，并洗匀. （1）从中任意抽取1张，抽到的数字是奇数的概率是；4（2）从中任意抽取1张，并将所取卡片上的数字记作一次函数 y  kx  b 中的 k；再从余下的卡片中任意抽取1张，并将所取卡片上的数字记作一次函数 y  kx  b 中的树状图或列表的方法，求这个一次函数的图象经过第一、二、四象限的概率. b .利用画 23.京沪铁路是我国东部沿海地区纵贯南北的交通大动脉，全长1462km ，是我国最繁忙的铁路干线之一.如果从北京到上海的客车速度是货车速度的2倍，客车比货车少用 6h ，那么货车的速度是多少？（精确到 0.1km / h 24.如图，在平行四边形 ABCD 中， DB  DA ，点 CB 的延长线于点，连接 AE ）F是 AB 的中点，连接 DF 并延长，交E.（1）求证：四边形 AEBD 是菱形；（2）若 DC  10 25.如图，在 ABC 中， AB  AC 心，OE 为半径作半圆，交 AO 于点，tan DCB  3，求菱形 AEBD 的面积. ，AO  BC 于点 O，OE  AB 于点 E ，以点O 为圆 F.（1）求证： AC 是 O 的切线；（2）若点 AO 的中点，OE  3，求图中阴影部分的面积； F是（3）在（2）的条件下，点的长. P是BC 边上的动点，当 PE  PF 取最小值时，直接写出 BP 26.“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量（件）与销售单价（元）之间存在一次函数关系，如图所示. yx5（1）求 y 与 x 之间的函数关系式；（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围. 27.问题呈现如图1，在边长为1的正方形网格中，连接格点，求 tan CPN 的值. D 、 N 和 E 、C ， DN 与 EC 相交于点 P 方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形.观察发现问题中CPN 不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题.比如连接格点，可得 MN / /EC ，则 DNM  CPN ，连接 DM ，那么 CPN 就变换到中 RtDMN M、 N .问题解决（1）直接写出图1中 tan CPN 的值为_________；（2）如图2，在边长为1的正方形网格中， AN 思维拓展与CM 相交于点 P ，求 cosCPN 的值； 6（3）如图3， AB  BC ，AB  4BC ，点 AB 上，且 AM  BC ，延长CB M在到 N ，使BN  2BC ，连接 AN 交CM 的延长线于点 P ，用上述方法构造网格求 CPN 的度数 .28.如图1，四边形OABC 是矩形，点出发，沿OA以每秒1个单位长度的速度向点秒2个单位长度的速度向点运动，当点与点 A的坐标为 (3,0)，点运动，同时点重合时运动停止.设运动时间为t c的坐标为 (0,6) .点从点出发，沿 AB 以每秒. P 从点O AQABPA（1）当t  2时，线段 PQ 的中点坐标为________；（2）当 CBQ PAQ 相似时，求的值；（3）当t 1时，抛物线 y  x2  bx  c 经过点为，如图2所示.问该抛物线上是否存在点出所有满足条件的点坐标；若不存在，说明理由. 与tP、Q两点，与 y轴交于点 M ，抛物线的顶 1KD，使 MQD  MKQ ，若存在，求 2D7参考答案一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的．题号 1A2C3B4B5A6C7C8A选项二、填空题：本大题共4小题，每小题5分，共20分． 39． 7104 　　　　　10． 2(3 x)(3 x) 　　　　　11．12．2018 410 11313．14．  3  x  　　　　　15． 2 2　　　　16． m  且m  0 325  13 216 12 17． (, ) 　　　　18． 55三、解答：本大共6小题题题满须说证过骤程和演算步．，分70分．解答写出文字明、明19．解：（1）原式  2  2  3  3  4 （2）原式  4×2  9 12x  4×2  9 12x  8 20．解：（1） 2  (5)  2 2  5  1 79x  2x  y  2 13（2）由题意得 ∴x  y  .4y  x  1 49y   21．（1）∵羽毛球占18% ，羽毛球有9人 ∴9 18%  50（人）总共50人，所以游泳和其他50  20 10  9 11 （2）∵自行车10人，总共50人即a  b 11 ∴10 503600  720 （3）篮球学生20人，总共50人 20 501200  480人答：该校最喜爱的省运动会项目是篮球的学生人数为480人. 122．解：（1）总共有四个，奇数有两个，所以概率就是 2  4  2（2）根据题意得：一次函数图形过第一、二、四象限，则 k  0,b  0 3 1 1 1 1 4  3 4 4  3 66  3 46613∴图象经过第一、二、四象限的概率是 4 12  .823．解：设货车的速度为 xkm/ h 1462 1462 由题意得  6  x 121.8 x2x 经检验 x 121.8是该方程的解答：货车的速度是121.8千米/小时. 24．解：（1）∵四边形 ABCD 是平行四边形 ∴∵AD // BC ，∴ ADE  DEB AB 的中点，∴ AF  BF BFE 中， ADE  DEB, AF  BF,AFD  BFE AD // BC ，∴四边形 AEBD 是平行四边形 DB  DA，∴四边形 AEBD 是菱形 F是∴在 AFD ∵与∵（2）∵四边形 AEBD 是菱形， DB  DA ∴∴AD  BD  BE  BC ，ADE  BDE,BDC  BCD AD // BC ADE  BDE  BDC  BCD 1800 BDE  BDC  900 ∵∴∴∵ DC  10 ， tan DCB  3 DE ∴ 3， DC  3 10 DC ∴ SAEBD  AB  DE  2  10 3 10 2 15 . 25.（1）过 O作AC 垂线OM ，垂足为 M∵∴AB  AC AO 平分 BAC ，AO  BC ∵OE  AB,OM  AC ∴∵∴∴OE  OM OE 为⊙ OM 为⊙ AC 是⊙ O 的半径， O的半径， O的切线（2）∵OM  OE  OF  3 且F是OA的中点 ∴∴AO  6 ， AE  3 3， 9SAEO  AO  AE  2  329∵∴OE  AB EOF  600 99 600 3 即S扇形OEF ，3600 23∴ S阴影 3   22（3）作 B关于 BC 的对称点 G，交 BC 于，H，连接 FG 交 BC 于 P 此时 PE  PF 最小由（2）知 EOF  600 ，EAO  300 ∴∵B  600 EO  3 323∴EG  3 ， EH  ，BH  2∵∴EG  BC ，FO  BC EHP FOP ∽EH HP 3212∴3  即2HP  OP FO PO 3∵ BO  HP  OP  3 ， 233∴∴3HP  BP  3即HP   3 ，22332.226.（1）设 y  kx  b ，将 (40,300),(55,150)代入，得 40k  b  300 k  10 55k  b 150 b  700 ∴y  10x  700 （2）设利润为 w 元 w  (x  3)(10x  700)  10×2 1000x  21000  10(x  50)2  4000 ∵y  240 ∴10x  700  240 解得 x  46 10 ∴x  46 时， ymax  3840 元答：单价为46元时，利润最大为3840元. （3）由题意得 w 150  10×2 1000x  21000 150  10×2 1000x  21150 ∴10×2 1000x  2115  360 45  x  55 即(x  45)(x  55)  0 则答：单价的范围是45元到55元. 27.（1）如图进行构造（2） CPN  EAN ∵EA  EN ，AE  EN ∴CPN  EAN  450 2∴cosCPN  2（3） CPN  FAN  450 ，证明同（2）. 28.（1）∵t  2，∴OP  2, AP 1, AQ  2 ∴∴P(2,0),Q(3,4) ，PQ 的中点坐标是 (2.5,2) （2）由题意得 PA  3 t, AQ  2t, BQ  6  2t 且有两种情况 ①CBA ∽PAQ CB BQ 36  2t 2t 9  3 5   t  AP AQ 3 t 2∵t  3 9  3 5 ∴t  2②CBA ∽ QAP 11 CB BQ 36  2t 34  t  （t  3 舍去） AQ AP 2t 3 t 9  3 5 3综上所述t  或t  . 24（3）作 KH  MQ ，则 KH 垂直平分 MQ ，1∴MKH  MKQ 223tan D QM tan D2QM  tan MKH  1223∴D2Q ： y  x  4 ， D Q ：y  x ， 132 4 D1( , ) 3 9 2 40 D2 ( , 3 9 ，) . 12 13 14 15 16 17 18 19 20 21 22 23 24