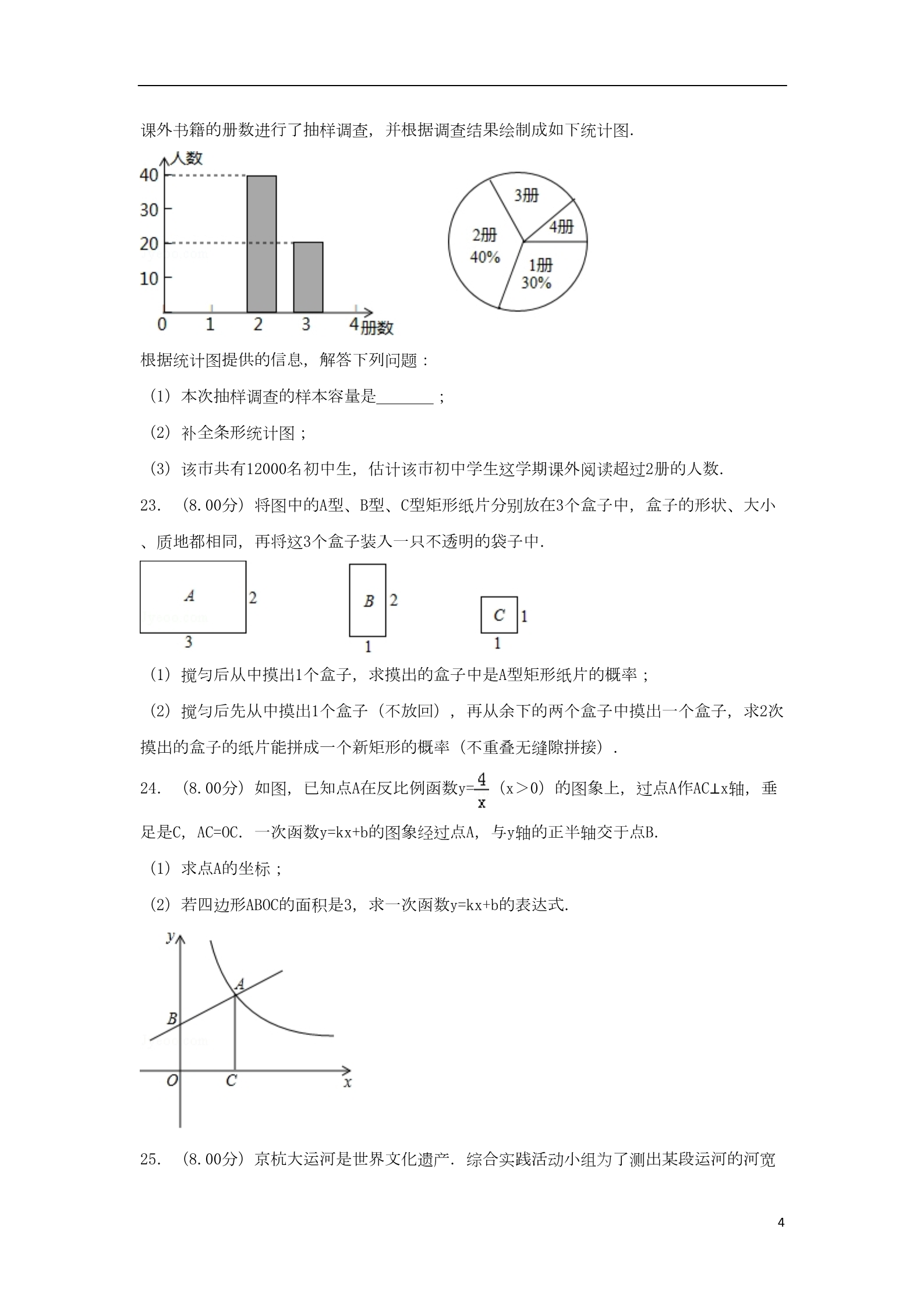
江苏省常州市2018年中考数学真题试题（含解析）

江苏省常州市2018年中考数学真题试题一、选择题（本大题共8小题，每小题2分，共16分.在每小题所给出的四个选项中，只有一项是正确的） 1．（2.00分）﹣3的倒数是（　　） A．﹣3 B．3 2．（2.00分）已知苹果每千克m元，则2千克苹果共多少元？（　　） A．m﹣2 B．m+2 C． D．2m 3．（2.00分）下列图形中，哪一个是圆锥的侧面展开图？（　　） C．﹣ D． A． 4．（2.00分）一个正比例函数的图象经过（2，﹣1），则它的表达式为（　　） A．y=﹣2x B．y=2x C． D． B． C． D． 5．（2.00分）下列命题中，假命题是（　　） A．一组对边相等的四边形是平行四边形 B．三个角是直角的四边形是矩形 C．四边相等的四边形是菱形 D．有一个角是直角的菱形是正方形 6．（2.00分）已知a为整数，且 A．1 B．2 C．3 D．4 ，则a等于（　　） 7．（2.00分）如图，AB是⊙O的直径，MN是⊙O的切线，切点为N，如果∠MNB=52°，则∠NO A的度数为（　　） A．76° B．56° C．54° D．52° 8．（2.00分）某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为1的半圆形量角器中，画一个直径为1的圆，把刻度尺CA的0刻度固定在半圆的圆心O处，刻度尺可以 1绕点O旋转．从图中所示的图尺可读出sin∠AOB的值是（　　） A． B． C． D．　二、填空题（本大题共10小题，每小题2分，共20分.不需写出解答过程，请把答案直接写在答题卡相应位置上） 9．（2.00分）计算：|﹣3|﹣1=　 10．（2.00分）化简： =　 11．（2.00分）分解因式：3×2﹣6x+3=　 12．（2.00分）已知点P（﹣2，1），则点P关于x轴对称的点的坐标是　　．　．　．　． 13．（2.00分）地球与月球的平均距离大约384000km，用科学计数法表示这个距离为　　km． 14．（2.00分）中华文化源远流长，如图是中国古代文化符号的太极图，圆中的黑色部分和白色部分关于圆心中心对称．在圆内随机取一点，则此点取黑色部分的概率是　　． 15．（2.00分）如图，在▱ABCD中，∠A=70°，DC=DB，则∠CDB=　　． 16．（2.00分）如图，△ABC是⊙O的内接三角形，∠BAC=60°，的长是径是　．，则⊙O的半 217．（2.00分）下面是按一定规律排列的代数式：a2，3a4，5a6，7a8，…则第8个代数式是　　．18．（2.00分）如图，在△ABC纸板中，AC=4，BC=2，AB=5，P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是　　．　三、解答题（本大题共10小题，共84分.请在答题卡指定区域内作答，如无特殊说明，解答应写出文字说明、演算步骤或推理过程） 19．（6.00分）计算：|﹣1|﹣ ﹣（1﹣ ）0+4sin30°． 20．（8.00分）解方程组和不等式组：（1）（2） 21．（8.00分）如图，把△ABC沿BC翻折得△DBC．（1）连接AD，则BC与AD的位置关系是　　．（2）不在原图中添加字母和线段，只加一个条件使四边形ABDC是平行四边形，写出添加的条件，并说明理由． 22．（8.00分）为了解某市初中学生课外阅读情况，调查小组对该市这学期初中学生阅读 3课外书籍的册数进行了抽样调查，并根据调查结果绘制成如下统计图．根据统计图提供的信息，解答下列问题：（1）本次抽样调查的样本容量是　（2）补全条形统计图；　；（3）该市共有12000名初中生，估计该市初中学生这学期课外阅读超过2册的人数． 23．（8.00分）将图中的A型、B型、C型矩形纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．（1）搅匀后从中摸出1个盒子，求摸出的盒子中是A型矩形纸片的概率；（2）搅匀后先从中摸出1个盒子（不放回），再从余下的两个盒子中摸出一个盒子，求2次摸出的盒子的纸片能拼成一个新矩形的概率（不重叠无缝隙拼接）． 24．（8.00分）如图，已知点A在反比例函数y= （x＞0）的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图象经过点A，与y轴的正半轴交于点B．（1）求点A的坐标；（2）若四边形ABOC的面积是3，求一次函数y=kx+b的表达式． 25．（8.00分）京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽 4（岸沿是平行的），如图，在岸边分别选定了点A、B和点C、D，先用卷尺量得AB=160m，CD =40m，再用测角仪测得∠CAB=30°，∠DBA=60°，求该段运河的河宽（即CH的长）． 26．（10.00分）阅读材料：各类方程的解法求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想转化，把未知转化为已知．用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x3+x2﹣2x=0，可以通过因式分解把它转化为x（x2+x﹣2）=0，解方程x=0和x2+x﹣2=0，可得方程x3+x2﹣2 x=0的解．（1）问题：方程x3+x2﹣2x=0的解是x1=0，x2=　　，x3=　　；（2）拓展：用“转化”思想求方程 =x的解；（3）应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长． 27．（10.00分）（1）如图1，已知EK垂直平分BC，垂足为D，AB与EK相交于点F，连接CF．求证：∠AFE=∠CFD．（2）如图2，在Rt△GMN中，∠M=90°，P为MN的中点． ①用直尺和圆规在GN边上求作点Q，使得∠GQM=∠PQN（保留作图痕迹，不要求写作法）； ②在①的条件下，如果∠G=60°，那么Q是GN的中点吗？为什么？ 528．（10.00分）如图，二次函数y=﹣ ，点A的坐标为（﹣4，0），P是抛物线上一点（点P与点A、B、C不重合）．（1）b=　，点B的坐标是　； +bx+2的图象与x轴交于点A、B，与y轴交于点C （2）设直线PB与直线AC相交于点M，是否存在这样的点P，使得PM：MB=1：2？若存在求出点P的横坐标；若不存在，请说明理由；（3）连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由．　6参考答案与试题解析一、选择题（本大题共8小题，每小题2分，共16分.在每小题所给出的四个选项中，只有一项是正确的） 1．（2.00分）﹣3的倒数是（　　） A．﹣3 B．3 C．﹣ D．【分析】根据倒数的定义可得﹣3的倒数是﹣ ．【解答】解：﹣3的倒数是﹣ 故选：C．．【点评】主要考查倒数的概念及性质．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．　2．（2.00分）已知苹果每千克m元，则2千克苹果共多少元？（　　） A．m﹣2 B．m+2 C． D．2m 【分析】根据苹果每千克m元，可以用代数式表示出2千克苹果的价钱．【解答】解：∵苹果每千克m元， ∴2千克苹果2m元，故选：D．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．　3．（2.00分）下列图形中，哪一个是圆锥的侧面展开图？（　　） A． B． C． D．【分析】根据圆锥的侧面展开图的特点作答．【解答】解：圆锥的侧面展开图是光滑的曲面，没有棱，只是扇形．故选：B．【点评】此题考查了几何体的展开图，注意圆锥的侧面展开图是扇形．　4．（2.00分）一个正比例函数的图象经过（2，﹣1），则它的表达式为（　　） 7A．y=﹣2x B．y=2x C． D．【分析】设该正比例函数的解析式为y=kx（k≠0），再把点（2，﹣1）代入求出k的值即可．【解答】解：设该正比例函数的解析式为y=kx（k≠0）， ∵正比例函数的图象经过点（2，﹣1）， ∴2=﹣k，解得k=﹣2， ∴这个正比例函数的表达式是y=﹣2x．故选：A．【点评】本题考查的是待定系数法求正比例函数的解析式，熟知正比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键．　5．（2.00分）下列命题中，假命题是（　　） A．一组对边相等的四边形是平行四边形 B．三个角是直角的四边形是矩形 C．四边相等的四边形是菱形 D．有一个角是直角的菱形是正方形【分析】根据矩形、正方形、平行四边形、菱形的判定即可求出答案．【解答】解：A、一组对边平行且相等的四边形是平行四边形，是假命题； B、三个角是直角的四边形是矩形，是真命题； C、四边相等的四边形是菱形，是真命题； D、有一个角是直角的菱形是正方形，是真命题；故选：A．【点评】本题考查菱形、矩形和平行四边形的判定与命题的真假区别，关键是根据矩形、正方形、平行四边形、菱形的判定解答．　6．（2.00分）已知a为整数，且 A．1 B．2 C．3 D．4 【分析】直接利用【解答】解：∵a为整数，且，则a等于（　　），接近的整数是2，进而得出答案．，8∴a=2．故选：B．【点评】此题主要考查了估算无理数大小，正确得出无理数接近的有理数是解题关键．　7．（2.00分）如图，AB是⊙O的直径，MN是⊙O的切线，切点为N，如果∠MNB=52°，则∠NO A的度数为（　　） A．76° B．56° C．54° D．52° 【分析】先利用切线的性质得∠ONM=90°，则可计算出∠ONB=38°，再利用等腰三角形的性质得到∠B=∠ONB=38°，然后根据圆周角定理得∠NOA的度数．【解答】解：∵MN是⊙O的切线， ∴ON⊥NM， ∴∠ONM=90°， ∴∠ONB=90°﹣∠MNB=90°﹣52°=38°， ∵ON=OB， ∴∠B=∠ONB=38°， ∴∠NOA=2∠B=76°．故选：A．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．　8．（2.00分）某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为1的半圆形量角器中，画一个直径为1的圆，把刻度尺CA的0刻度固定在半圆的圆心O处，刻度尺可以绕点O旋转．从图中所示的图尺可读出sin∠AOB的值是（　　） 9A． B． C． D．【分析】如图，连接AD．只要证明∠AOB=∠ADO，可得sin∠AOB=sin∠ADO= = 【解答】解：如图，连接AD．；∵OD是直径， ∴∠OAD=90°， ∵∠AOB+∠AOD=90°，∠AOD+∠ADO=90°， ∴∠AOB=∠ADO， ∴sin∠AOB=sin∠ADO= = 故选：D．，【点评】本题考查圆周角定理、直径的性质、锐角三角函数等知识，解题的关键是学会用转化的思想思考问题，属于中考创新题目．　二、填空题（本大题共10小题，每小题2分，共20分.不需写出解答过程，请把答案直接写在答题卡相应位置上） 9．（2.00分）计算：|﹣3|﹣1=　2　．【分析】原式利用绝对值的代数意义，以及减法法则计算即可求出值．【解答】解：原式=3﹣1=2．故答案为：2 【点评】此题考查了有理数的减法，熟练掌握运算法则是解本题的关键．　10 10．（2.00分）化简： =　1　．【分析】原式利用同分母分式的减法法则计算即可．【解答】解：原式= 故答案为：1 =1，【点评】此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．　11．（2.00分）分解因式：3×2﹣6x+3=　3（x﹣1）2　．【分析】先提取公因式3，再对余下的多项式利用完全平方公式继续分解．【解答】解：3×2﹣6x+3， =3（x2﹣2x+1）， =3（x﹣1）2．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．　12．（2.00分）已知点P（﹣2，1），则点P关于x轴对称的点的坐标是　（﹣2，﹣1）　．【分析】根据关于x轴对称的点的横坐标相等，纵坐标互为相反数，可得答案．【解答】解：点P（﹣2，1），则点P关于x轴对称的点的坐标是（﹣2，﹣1），故答案为：（﹣2，﹣1）．【点评】本题考查了关于x轴对称的对称点，利用关于x轴对称的点的横坐标相等，纵坐标互为相反数是解题关键．　13．（2.00分）地球与月球的平均距离大约384000km，用科学计数法表示这个距离为　 3.84×105　km．【分析】科学记数法的一般形式为：a×10n，在本题中a应为3.84，10的指数为6﹣1=5．【解答】解：384 000=3.84×105km．故答案为3.84×105．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤ |a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　11 14．（2.00分）中华文化源远流长，如图是中国古代文化符号的太极图，圆中的黑色部分和白色部分关于圆心中心对称．在圆内随机取一点，则此点取黑色部分的概率是　．【分析】根据中心对称图形的性质得到圆中的黑色部分和白色部分面积相等，根据概率公式计算即可．【解答】解：∵圆中的黑色部分和白色部分关于圆心中心对称， ∴圆中的黑色部分和白色部分面积相等， ∴在圆内随机取一点，则此点取黑色部分的概率是故答案为：，．【点评】本题考查的是概率公式、中心对称图形，掌握概率公式是解题的关键．　15．（2.00分）如图，在▱ABCD中，∠A=70°，DC=DB，则∠CDB=　40°　．【分析】根据等腰三角形的性质，平行四边形的性质以及三角形内角和定理即可解决问题．【解答】解：∵四边形ABCD是平行四边形， ∴∠A=∠C=70°， ∵DC=DB， ∴∠C=∠DBC=70°， ∴∠CDB=180°﹣70°﹣70°=40°，故答案为40°．【点评】本题考查平行四边形的性质、等腰三角形的性质、三角形内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．　12 16．（2.00分）如图，△ABC是⊙O的内接三角形，∠BAC=60°，的长是径是　2　．，则⊙O的半【分析】连接OB、OC，利用弧长公式转化为方程求解即可；【解答】解：连接OB、OC． ∵∠BOC=2∠BAC=120°，的长是，∴=，∴r=2，故答案为2．【点评】本题考查三角形的外接圆与外心，圆周角定理，弧长的计算等知识，解题的关键是熟练掌握弧长公式，属于中考常考题型．　17．（2.00分）下面是按一定规律排列的代数式：a2，3a4，5a6，7a8，…则第8个代数式是　 15a16　．【分析】直接利用已知单项式的次数与系数特点得出答案．【解答】解：∵a2，3a4，5a6，7a8，… ∴单项式的次数是连续的偶数，系数是连续的奇数， ∴第8个代数式是：（2×8﹣1）a2×8=15a16．故答案为：15a16．【点评】此题主要考查了单项式，正确得出单项式次数与系数的变化规律是解题关键．　18．（2.00分）如图，在△ABC纸板中，AC=4，BC=2，AB=5，P是AC上一点，过点P沿直线剪 13 下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是　 3≤AP＜4　．【分析】分四种情况讨论，依据相似三角形的对应边成比例，即可得到AP的长的取值范围．【解答】解：如图所示，过P作PD∥AB交BC于D或PE∥BC交AB于E，则△PCD∽△ACB或△APE∽△AC B，此时0＜AP＜4；如图所示，过P作∠APF=∠B交AB于F，则△APF∽△ABC，此时0＜AP≤4；如图所示，过P作∠CPG=∠CBA交BC于G，则△CPG∽△CBA，此时，△CPG∽△CBA，当点G与点B重合时，CB2=CP×CA，即22=CP×4， ∴CP=1，AP=3， ∴此时，3≤AP＜4；综上所述，AP长的取值范围是3≤AP＜4．故答案为：3≤AP＜4．【点评】本题主要考查了相似三角形的性质，相似三角形的对应角相等，对应边的比相等．14 　三、解答题（本大题共10小题，共84分.请在答题卡指定区域内作答，如无特殊说明，解答应写出文字说明、演算步骤或推理过程） 19．（6.00分）计算：|﹣1|﹣ ﹣（1﹣ ）0+4sin30°．【分析】直接利用特殊角的三角函数值以及绝对值的性质、零指数幂的性质分别化简得出答案．【解答】解：原式=1﹣2﹣1+4× =1﹣2﹣1+2 =0．【点评】此题主要考查了实数运算，正确化简各数是解题关键．　20．（8.00分）解方程组和不等式组：（1）（2）【分析】（1）方程组利用加减消元法求出解即可；（2）分别求出不等式组中两不等式的解集，找出解集的公共部分即可．【解答】解：（1），①+②得：x=2，把x=2代入②得：y=﹣1，所以方程组的解为：；（2），解不等式①得：x≥3；解不等式②得：x≥﹣1，所以不等式组的解集为：x≥3．【点评】此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．　21．（8.00分）如图，把△ABC沿BC翻折得△DBC．（1）连接AD，则BC与AD的位置关系是　BC⊥AB　． 15 （2）不在原图中添加字母和线段，只加一个条件使四边形ABDC是平行四边形，写出添加的条件，并说明理由．【分析】（1）先由折叠知，AB=BD，∠ACB=∠DBC，进而判断出△AOB≌△DOB，最后用平角的定义即可得出结论；（2）由折叠得出∠ABC=∠DBC，∠ACB=∠DCB，再判断出∠ABC=∠ACB，进而得出∠ACB=∠DBC=∠A BC=∠DCB，最后用两边分别平行的四边形是平行四边形．【解答】解：（1）如图，连接AD交BC于O，由折叠知，AB=BD，∠ACB=∠DBC， ∵BO=BO， ∴△ABO≌△DBO（SAS）， ∴∠AOB=∠DOB， ∵∠AOB+∠DOB=180°， ∴∠AOB=∠DOB=90°， ∴BC⊥AD，故答案为：BC⊥AD；（2）添加的条件是AB=AC，理由：由折叠知，∠ABC=∠DBC，∠ACB=∠DCB， ∵AB=AC， ∴∠ABC=∠ACB， ∴∠ACB=∠DBC=∠ABC=∠DCB， ∴AC∥BD，AB∥CD， ∴四边形ABDC是平行四边形． 16 【点评】此题主要考查了折叠的性质，平行四边形的判定，等腰三角形的性质，全等三角形的判定和性质，判断出△ABO≌△DBO（SAS）是解本题的关键．　22．（8.00分）为了解某市初中学生课外阅读情况，调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查，并根据调查结果绘制成如下统计图．根据统计图提供的信息，解答下列问题：（1）本次抽样调查的样本容量是　100　；（2）补全条形统计图；（3）该市共有12000名初中生，估计该市初中学生这学期课外阅读超过2册的人数．【分析】（1）根据2册的人数除以占的百分比即可得到总人数；（2）求出1册的人数是100×30%=30人，4册的人数是100﹣30﹣40﹣20=10人，再画出即可；（3）先列出算式，再求出即可．【解答】解：（1）40÷40%=100（册），即本次抽样调查的样本容量是100，故答案为：100； 17 （2）如图：；（3）12000×（1﹣30%）=8400（人），答：估计该市初中学生这学期课外阅读超过2册的人数是8400人．【点评】本题考查了条形统计图、扇形统计图，总体、个体、样本、样本容量，用样本估计总体等知识点，两图结合是解题的关键．　23．（8.00分）将图中的A型、B型、C型矩形纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．（1）搅匀后从中摸出1个盒子，求摸出的盒子中是A型矩形纸片的概率；（2）搅匀后先从中摸出1个盒子（不放回），再从余下的两个盒子中摸出一个盒子，求2次摸出的盒子的纸片能拼成一个新矩形的概率（不重叠无缝隙拼接）．【分析】（1）直接利用概率公式计算可得；（2）画树状图得出所有等可能结果，从中找打2次摸出的盒子的纸片能拼成一个新矩形的结果数，利用概率公式计算可得．【解答】解：（1）搅匀后从中摸出1个盒子有3种等可能结果，所以摸出的盒子中是A型矩形纸片的概率为（2）画树状图如下：；18 由树状图知共有6种等可能结果，其中2次摸出的盒子的纸片能拼成一个新矩形的有4种结果，所以2次摸出的盒子的纸片能拼成一个新矩形的概率为 = ．【点评】此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．　24．（8.00分）如图，已知点A在反比例函数y= （x＞0）的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图象经过点A，与y轴的正半轴交于点B．（1）求点A的坐标；（2）若四边形ABOC的面积是3，求一次函数y=kx+b的表达式．【分析】（1）根据反比例函数k值的几何意义可求点A的坐标；（2）根据梯形的面积公式可求点B的坐标，再根据待定系数法可求一次函数y=kx+b的表达式．【解答】解：（1）∵点A在反比例函数y= （x＞0）的图象上，AC⊥x轴，AC=OC， ∴AC•OC=4， ∴AC=OC=2， ∴点A的坐标为（2，2）；（2）∵四边形ABOC的面积是3， ∴（OB+2）×2÷2=3， 19 解得OB=1， ∴点B的坐标为（0，1），依题意有，解得．故一次函数y=kx+b的表达式为y= x+1．【点评】考查了反比例函数与一次函数的交点问题，关键是熟练掌握反比例函数k值的几何意义、梯形的面积、待定系数法求一次函数解析式．　25．（8.00分）京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点A、B和点C、D，先用卷尺量得AB=160m，CD =40m，再用测角仪测得∠CAB=30°，∠DBA=60°，求该段运河的河宽（即CH的长）．【分析】过D作DE⊥AB，可得四边形CHED为矩形，由矩形的对边相等得到两对对边相等，分别在直角三角形ACH与直角三角形BDE中，设CH=DE=xm，利用锐角三角函数定义表示出AH与B E，由AH+HE+EB=AB列出方程，求出方程的解即可得到结果．【解答】解：过D作DE⊥AB，可得四边形CHED为矩形， ∴HE=CD=40m，设CH=DE=xm，在Rt△BDE中，∠DBA=60°， ∴BE= xm，在Rt△ACH中，∠BAC=30°， ∴AH= xm，由AH+HE+EB=AB=160m，得到 x+40+ x=160，解得：x=30 ，即CH=30 m，则该段运河的河宽为30 m． 20 【点评】此题考查了解直角三角形的应用，熟练掌握锐角三角函数定义是解本题的关键．　26．（10.00分）阅读材料：各类方程的解法求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想转化，把未知转化为已知．用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x3+x2﹣2x=0，可以通过因式分解把它转化为x（x2+x﹣2）=0，解方程x=0和x2+x﹣2=0，可得方程x3+x2﹣2 x=0的解．（1）问题：方程x3+x2﹣2x=0的解是x1=0，x2=　﹣2　，x3=　1　；（2）拓展：用“转化”思想求方程 =x的解；（3）应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长．【分析】（1）因式分解多项式，然后得结论；（2）两边平方，把无理方程转化为整式方程，求解，注意验根；（3）设AP的长为xm，根据勾股定理和BP+CP=10，可列出方程，由于方程含有根号，两边平方，把无理方程转化为整式方程，求解，【解答】解：（1）x3+x2﹣2x=0， x（x2+x﹣2）=0， x（x+2）（x﹣1）=0 21 所以x=0或x+2=0或x﹣1=0 ∴x1=0，x2=﹣2，x3=1；故答案为：﹣2，1；（2） =x，方程的两边平方，得2x+3=x2 即x2﹣2x﹣3=0 （x﹣3）（x+1）=0 ∴x﹣3=0或x+1=0 ∴x1=3，x2=﹣1，当x=﹣1时， = =1≠﹣1，所以﹣1不是原方程的解．所以方程 =x的解是x=3；（3）因为四边形ABCD是矩形，所以∠A=∠D=90°，AB=CD=3m 设AP=xm，则PD=（8﹣x）m 因为BP+CP=10， BP= ∴，CP= +=10 ∴=10﹣ 两边平方，得（8﹣x）2+9=100﹣20 整理，得5 =4x+9 +9+x2 两边平方并整理，得x2﹣8x+16=0 即（x﹣4）2=0 所以x=4．经检验，x=4是方程的解．答：AP的长为4m．【点评】本题考查了转化的思想方法，一元二次方程的解法．解无理方程是注意到验根．解决（3）时，根据勾股定理和绳长，列出方程是关键． 22 　27．（10.00分）（1）如图1，已知EK垂直平分BC，垂足为D，AB与EK相交于点F，连接CF．求证：∠AFE=∠CFD．（2）如图2，在Rt△GMN中，∠M=90°，P为MN的中点． ①用直尺和圆规在GN边上求作点Q，使得∠GQM=∠PQN（保留作图痕迹，不要求写作法）； ②在①的条件下，如果∠G=60°，那么Q是GN的中点吗？为什么？【分析】（1）只要证明FC=FB即可解决问题；（2）①作点P关于GN的对称点P′，连接P′M交GN于Q，连接PQ，点Q即为所求． ②结论：Q是GN的中点．想办法证明∠N=∠QMN=30°，∠G=∠GMQ=60°，可得QM=QN，QM=QG；【解答】（1）证明：如图1中， ∵EK垂直平分线段BC， ∴FC=FB， ∴∠CFD=∠BFD， ∵∠BFD=∠AFE， ∴∠AFE=∠CFD．（2）①作点P关于GN的对称点P′，连接P′M交GN于Q，连接PQ，点Q即为所求． 23 ②结论：Q是GN的中点．理由：设PP′交GN于K． ∵∠G=60°，∠GMN=90°， ∴∠N=30°， ∵PK⊥KN， ∴PK=KP′= PN， ∴PP′=PN=PM， ∴∠P′=∠PMP′， ∵∠NPK=∠P′+∠PMP′=60°， ∴∠PMP′=30°， ∴∠N=∠QMN=30°，∠G=∠GMQ=60°， ∴QM=QN，QM=QG， ∴QG=QN， ∴Q是GN的中点．【点评】本题考查作图﹣复杂作图、线段的垂直平分线的性质、直角三角形斜边中线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．　28．（10.00分）如图，二次函数y=﹣ +bx+2的图象与x轴交于点A、B，与y轴交于点C ，点A的坐标为（﹣4，0），P是抛物线上一点（点P与点A、B、C不重合）．（1）b=　﹣ 　，点B的坐标是　（，0）　；（2）设直线PB与直线AC相交于点M，是否存在这样的点P，使得PM：MB=1：2？若存在求出点P的横坐标；若不存在，请说明理由；（3）连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由． 24 【分析】（1）由点A的坐标，利用二次函数图象上点的坐标特征可求出b的值，代入y=0求出x值，进而可得出点B的坐标；（2）代入x=0求出y值，进而可得出点C的坐标，由点A、C的坐标利用待定系数法可求出直线AC的解析式，假设存在，设点M的坐标为（m， m+2），分B、P在直线AC的同侧和异侧两种情况考虑，由点B、M的坐标结合PM：MB=1：2即可得出点P的坐标，再利用二次函数图象上点的坐标特征可得出关于m的一元二次方程，解之即可得出结论；（3）作∠CBA的角平分线，交y轴于点E，过点E作EF⊥BC于点F，设OE=n，则CE=2﹣n，EF=n ，利用面积法可求出n值，进而可得出 = = ，结合∠AOC=90°=∠BOE可证出△AOC∽△BO E，根据相似三角形的性质可得出∠CAO=∠EBO，再根据角平分线的性质可得出∠CBA=2∠EBO= 2∠CAB，此题得解．【解答】解：（1）∵点A（﹣4，0）在二次函数y=﹣ +bx+2的图象上， ∴﹣ ﹣4b+2=0， ∴b=﹣ ．当y=0时，有﹣ x2﹣ x+2=0，解得：x1=﹣4，x2= ，∴点B的坐标为（，0）．故答案为：﹣ ；（，0）．（2）当x=0时，y=﹣ x2﹣ x+2=2， ∴点C的坐标为（0，2）．设直线AC的解析式为y=kx+c（k≠0），将A（﹣4，0）、C（0，2）代入y=kx+c中， 25 得：，解得：，∴直线AC的解析式为y= x+2．假设存在，设点M的坐标为（m， m+2）． ①当点P、B在直线AC的异侧时，点P的坐标为（ m﹣ ， m+3）， ∵点P在抛物线y=﹣ x2﹣ x+2上， ∴m+3=﹣ ×（ m﹣ ）2﹣ ×（ m﹣ ）+2，整理，得：12m2+20m+9=0． ∵△=202﹣4×12×9=﹣32＜0， ∴方程无解，即不存在符合题意得点P； ②当点P、B在直线AC的同侧时，点P的坐标为（ m+ ， m+1）， ∵点P在抛物线y=﹣ x2﹣ x+2上， ∴m+1=﹣ ×（ m+ ）2﹣ ×（ m+ ）+2，整理，得：4m2+44m﹣9=0，解得：m1=﹣ ，m2= ，∴点P的横坐标为﹣2﹣ 或﹣2+ ．综上所述：存在点P，使得PM：MB=1：2，点P的横坐标为﹣2﹣ （3）∠CBA=2∠CAB，理由如下：或﹣2+ ．作∠CBA的角平分线，交y轴于点E，过点E作EF⊥BC于点F，如图2所示． ∵点B（，0），点C（0，2）， ∴OB= ，OC=2，BC= ．设OE=n，则CE=2﹣n，EF=n，由面积法，可知： OB•CE= BC•EF，即（2﹣n）= n，解得：n= ．26 ∵ = = ，∠AOC=90°=∠BOE， ∴△AOC∽△BOE， ∴∠CAO=∠EBO， ∴∠CBA=2∠EBO=2∠CAB．【点评】题考查了二次函数图象上点的坐标特征、待定系数法求一次函数解析式、三角形的面积、勾股定理、一次函数图象上点的坐标特征以及相似三角形的判定与性质，解题的关键是：（1）由点A的坐标，利用二次函数图象上点的坐标特征求出b的值；（2）分B、P 在直线AC的同侧和异侧两种情况找出点P的坐标；（3）构造相似三角形找出两角的数量关系． 27