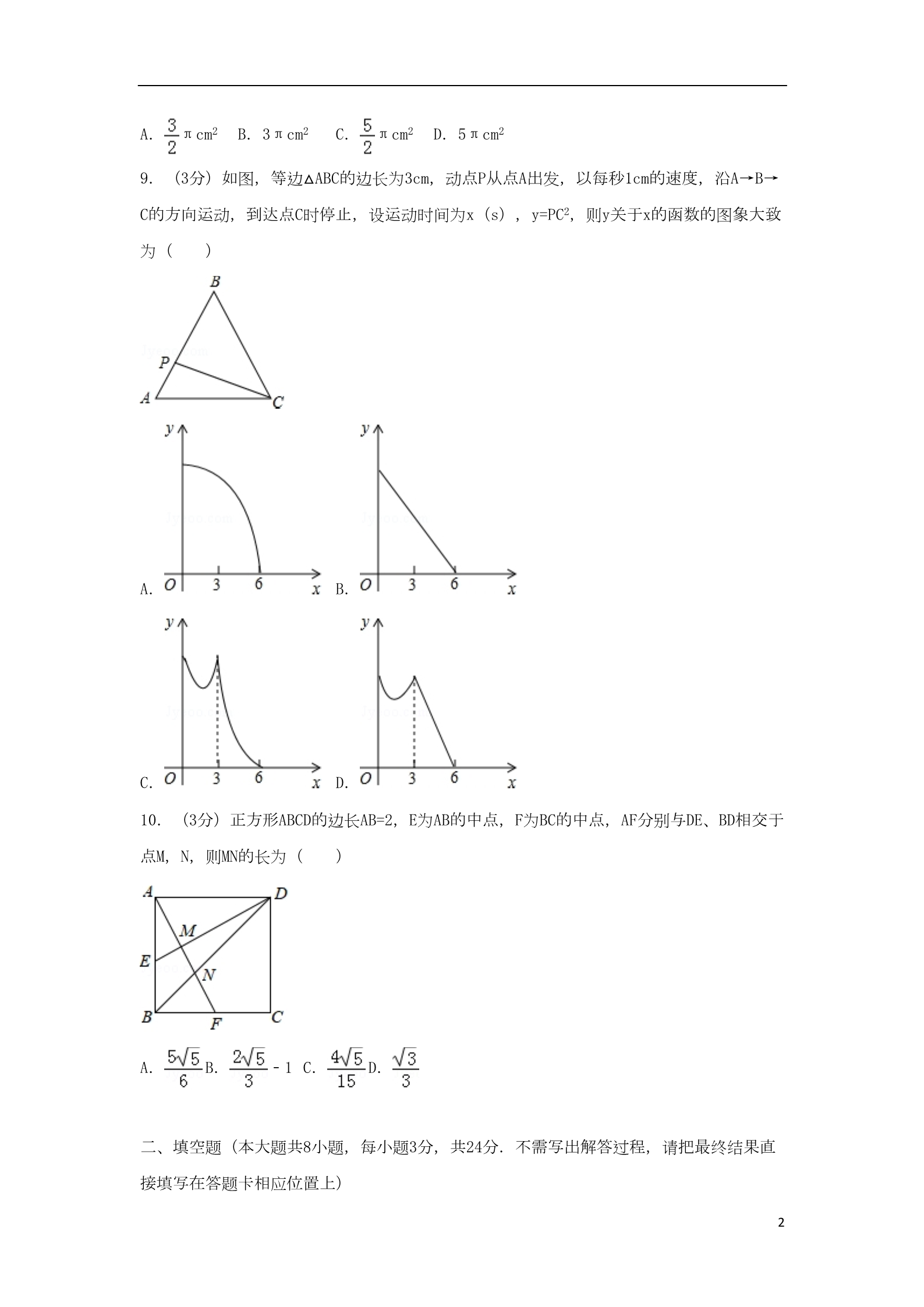
江苏省南通市2018年中考数学真题试题（含解析）

江苏省南通市2018年中考数学真题试题一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 1．（3分）的值是（　　） A．4 B．2 C．±2 D．﹣2 2．（3分）下列计算中，正确的是（　　） A．a2•a3=a5 B．（a2）3=a8 C．a3+a2=a5 D．a8÷a4=a2 3．（3分）若在实数范围内有意义，则x的取值范围是（　　） A．x≥3 B．x＜3 C．x≤3 D．x＞3 4．（3分）函数y=﹣x的图象与函数y=x+1的图象的交点在（　　） A．第一象限 B．第二象限 C．第三象限 D．第四象限 5．（3分）下列说法中，正确的是（　　） A．一个游戏中奖的概率是，则做10次这样的游戏一定会中奖 B．为了了解一批炮弹的杀伤半径，应采用全面调查的方式 C．一组数据8，8，7，10，6，8，9的众数是8 D．若甲组数据的方差是0.1，乙组数据的方差是0.2，则乙组数据比甲组数据波动小 6．（3分）篮球比赛规定：胜一场得3分，负一场得1分，某篮球队共进行了6场比赛，得了 12分，该队获胜的场数是（　　） A．2 B．3 C．4 D．5 7．（3分）如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于点E、F ，再分别以E、F为圆心，大于 EF的同样长为半径作圆弧，两弧交于点P，作射线AP，交CD 于点M，若∠ACD=110°，则∠CMA的度数为（　　） A．30° B．35° C．70° D．45° 8．（3分）一个空间几何体的主视图和左视图都是边长为2cm的正三角形，俯视图是一个圆，那么这个几何体的表面积是（　　） 1A． πcm2 B．3πcm2 C． πcm2 D．5πcm2 9．（3分）如图，等边△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→ C的方向运动，到达点C时停止，设运动时间为x（s），y=PC2，则y关于x的函数的图象大致为（　　） A． B． C． D． 10．（3分）正方形ABCD的边长AB=2，E为AB的中点，F为BC的中点，AF分别与DE、BD相交于点M，N，则MN的长为（　　） A． B． ﹣1 C． D．　二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把最终结果直接填写在答题卡相应位置上） 211．（3分）“辽宁舰“最大排水量为67500吨，将67500用科学记数法表示为　 12．（3分）分解因式：a3﹣2a2b+ab2=　　．　． 13．（3分）已知正n边形的每一个内角为135°，则n=　 14．（3分）某厂一月份生产某机器100台，计划三月份生产160台．设二、三月份每月的平均增长率为x，根据题意列出的方程是　． 15．（3分）如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=3，AB=5，OD⊥BC于点D，则 OD的长为　．　． 16．（3分）下面是“作一个30°角”的尺规作图过程．已知：平面内一点A．求作：∠A，使得∠A=30°．作图：如图，（1）作射线AB；（2）在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；（3）以C为圆心，OC为半径作弧，与⊙O交于点D，作射线AD，∠DAB即为所求的角．请回答：该尺规作图的依据是　　． 17．（3分）如图，在△ABC中，∠C=90°，AC=3，BC=4，点O是BC中点，将△ABC绕点O旋转得△A′B’C，则在旋转过程中点A、C′两点间的最大距离是　． 318．（3分）在平面直角坐标系xOy中，过点A（3，0）作垂直于x轴的直线AB，直线y=﹣x+b 与双曲线y= 交于点P（x1，y1），Q（x2，y2），与直线AB交于点R（x3，y3），若y1＞y2＞ y3时，则b的取值范围是　　．　三、解答题（本大题共10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤） 19．（10分）（1）计算：| ﹣2|+20130﹣（﹣ ）﹣1+3tan30°；（2）解方程： =﹣3． 20．（8分）解不等式组，并写出x的所有整数解． 21．（8分）“校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题：（1）接受问卷调查的学生共有　　人，扇形统计图中“了解”部分所对应扇形的圆心角为　　度； 4（2）请补全条形统计；（3）若该中学共有学生1200人，估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数． 22．（8分）四张扑克牌的点数分别是2，3，4，8，除点数不同外，其余都相同，将它们洗匀后背面朝上放在桌上．（1）从中随机抽取一张牌，求这张牌的点数是偶数的概率；（2）随机抽取一张牌不放回，接着再抽取一张牌，求这两张牌的点数都是偶数的概率． 23．（8分）如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60° 方向行驶12千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地的距离．（结果保留根号） 24．（8分）如图，▱ABCD中，点E是BC的中点，连接AE并延长交DC延长线于点F．（1）求证：CF=AB；（2）连接BD、BF，当∠BCD=90°时，求证：BD=BF． 25．（8分）一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：（1）慢车的速度为　　km/h，快车的速度为　　km/h；（2）解释图中点C的实际意义并求出点C的坐标；（3）求当x为多少时，两车之间的距离为500km． 526．（12分）如图，△ABC中，AB=6cm，AC=4 cm，BC=2 cm，点P以1cm/s的速度从点B 出发沿边BA→AC运动到点C停止，运动时间为t s，点Q是线段BP的中点．（1）若CP⊥AB时，求t的值；（2）若△BCQ是直角三角形时，求t的值；（3）设△CPQ的面积为S，求S与t的关系式，并写出t的取值范围． 27．（12分）已知，正方形ABCD，A（0，﹣4），B（l，﹣4），C（1，﹣5），D（0，﹣5 ），抛物线y=x2+mx﹣2m﹣4（m为常数），顶点为M．（1）抛物线经过定点坐标是　　，顶点M的坐标（用m的代数式表示）是　　；（2）若抛物线y=x2+mx﹣2m﹣4（m为常数）与正方形ABCD的边有交点，求m的取值范围；（3）若∠ABM=45°时，求m的值． 628．（14分）如图，⊙O的直径AB=26，P是AB上（不与点A、B重合）的任一点，点C、D为⊙ O上的两点，若∠APD=∠BPC，则称∠CPD为直径AB的“回旋角”．（1）若∠BPC=∠DPC=60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；（2）若的长为 π，求“回旋角”∠CPD的度数；（3）若直径AB的“回旋角”为120°，且△PCD的周长为24+13 ，直接写出AP的长．　7参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 1．（3分）的值是（　　） A．4 B．2 C．±2 D．﹣2 【分析】根据算术平方根解答即可．【解答】解： =2，故选：B．【点评】此题考查算术平方根问题，关键是根据4的算术平方根是2解答．　2．（3分）下列计算中，正确的是（　　） A．a2•a3=a5 B．（a2）3=a8 C．a3+a2=a5 D．a8÷a4=a2 【分析】根据同底数幂的乘法、幂的乘方、合并同类项法则及同底数幂的除法逐一计算可得．【解答】解：A、a2•a3=a5，此选项正确； B、（a2）3=a6，此选项错误； C、a3、a2不能合并，此选项错误； D、a8÷a4=a4，此选项错误；故选：A．【点评】本题主要考查整式的运算，解题的关键是掌握同底数幂的乘法、幂的乘方、合并同类项法则及同底数幂的除法．　3．（3分）若在实数范围内有意义，则x的取值范围是（　　） A．x≥3 B．x＜3 C．x≤3 D．x＞3 【分析】根据二次根式有意义的条件；列出关于x的不等式，求出x的取值范围即可．【解答】解：∵ ∴x﹣3≥0，解得x≥3．故选：A．在实数范围内有意义，【点评】本题考查的是二次根式有意义的条件，熟知二次根式具有非负性是解答此题的关键． 8　4．（3分）函数y=﹣x的图象与函数y=x+1的图象的交点在（　　） A．第一象限 B．第二象限 C．第三象限 D．第四象限【分析】根据题目中的函数解析式可以求得这两个函数的交点坐标，从而可以解答本题．【解答】解：，解得，，∴函数y=﹣x的图象与函数y=x+1的图象的交点是（，），故函数y=﹣x的图象与函数y=x+1的图象的交点在第二象限，故选：B．【点评】本题考查两条直线相交或平行问题，解答本题的关键是明确题意，求出两个函数的交点坐标，利用函数的思想解答．　5．（3分）下列说法中，正确的是（　　） A．一个游戏中奖的概率是，则做10次这样的游戏一定会中奖 B．为了了解一批炮弹的杀伤半径，应采用全面调查的方式 C．一组数据8，8，7，10，6，8，9的众数是8 D．若甲组数据的方差是0.1，乙组数据的方差是0.2，则乙组数据比甲组数据波动小【分析】根据概率的意义可判断出A的正误；根据抽样调查与全面调查意义可判断出B的正误；根据众数和中位数的定义可判断出C的正误；根据方差的意义可判断出D的正误．【解答】解：A、一个游戏中奖的概率是项错误；，做10次这样的游戏也不一定会中奖，故此选 B、为了了解一批炮弹的杀伤半径，应采用抽样调查的方式，故此选项错误； C、一组数据8，8，7，10，6，8，9的众数和中位数都是8，故此选项正确； D、若甲组数据的方差是0.1，乙组数据的方差是0.2，则乙组数据比甲组数据波动大；故选：C．【点评】此题主要考查了概率、抽样调查与全面调查、众数和中位数、方差，关键是注意再找中位数时要把数据从小到大排列再找出位置处于中间的数． 9　6．（3分）篮球比赛规定：胜一场得3分，负一场得1分，某篮球队共进行了6场比赛，得了 12分，该队获胜的场数是（　　） A．2 B．3 C．4 D．5 【分析】设该队获胜x场，则负了（6﹣x）场，根据总分=3×获胜场数+1×负了的场数，即可得出关于x的一元一次方程，解之即可得出结论．【解答】解：设该队获胜x场，则负了（6﹣x）场，根据题意得：3x+（6﹣x）=12，解得：x=3．答：该队获胜3场．故选：B．【点评】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．　7．（3分）如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于点E、F ，再分别以E、F为圆心，大于 EF的同样长为半径作圆弧，两弧交于点P，作射线AP，交CD 于点M，若∠ACD=110°，则∠CMA的度数为（　　） A．30° B．35° C．70° D．45° 【分析】直接利用平行线的性质结合角平分线的作法得出∠CAM=∠BAM=35°，即可得出答案．【解答】解：∵AB∥CD，∠ACD=110°， ∴∠CAB=70°， ∵以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于点E、F，再分别以E、F为圆心，大于 EF的同样长为半径作圆弧，两弧交于点P，作射线AP，交CD于点M， ∴AP平分∠CAB， ∴∠CAM=∠BAM=35°， 10 ∵AB∥CD， ∴∠CMA=∠MAB=35°．故选：B．【点评】此题主要考查了基本作图以及平行线的性质，正确得出∠CAM=∠BAM是解题关键．　8．（3分）一个空间几何体的主视图和左视图都是边长为2cm的正三角形，俯视图是一个圆，那么这个几何体的表面积是（　　） A． πcm2 B．3πcm2 C． πcm2 D．5πcm2 【分析】根据三视图的知识可知该几何体为一个圆锥．又已知底面半径可求出母线长以及侧面积、底面积后即可求得其表面积．【解答】解：综合主视图，俯视图，左视图可以看出这个几何体应该是圆锥，且底面圆的半径为1，母线长为2，因此侧面面积为1×π×2=2π，底面积为π×（1）2=π．表面积为2π+π=3π；故选：B．【点评】此题考查由三视图判定几何体，本题中要先确定出几何体的面积，然后根据其侧面积的计算公式进行计算．本题要注意圆锥的侧面积的计算方法是圆锥的底面半径乘以圆周率再乘以母线长．　9．（3分）如图，等边△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→ C的方向运动，到达点C时停止，设运动时间为x（s），y=PC2，则y关于x的函数的图象大致为（　　） 11 A． B． C． D．【分析】需要分类讨论：①当0≤x≤3，即点P在线段AB上时，根据余弦定理知cosA= ，所以将相关线段的长度代入该等式，即可求得y与x的函数关系式，然后根据函数关系式确定该函数的图象．②当3＜x≤6，即点P在线段BC上时，y与x的函数关系式是y=（6﹣x）2=（x﹣6）2（3＜x≤6），根据该函数关系式可以确定该函数的图象．【解答】解：∵正△ABC的边长为3cm， ∴∠A=∠B=∠C=60°，AC=3cm． ①当0≤x≤3时，即点P在线段AB上时，AP=xcm（0≤x≤3）；根据余弦定理知cosA= 即 = ，，解得，y=x2﹣3x+9（0≤x≤3）；该函数图象是开口向上的抛物线；解法二：过C作CD⊥AB，则AD=1.5cm，CD= 点P在AB上时，AP=x cm，PD=|1.5﹣x|cm， cm， ∴y=PC2=（）2+（1.5﹣x）2=x2﹣3x+9（0≤x≤3）该函数图象是开口向上的抛物线； 12 ②当3＜x≤6时，即点P在线段BC上时，PC=（6﹣x）cm（3＜x≤6）；则y=（6﹣x）2=（x﹣6）2（3＜x≤6）， ∴该函数的图象是在3＜x≤6上的抛物线；故选：C．【点评】本题考查了动点问题的函数图象．解答该题时，需要对点P的位置进行分类讨论，以防错选．　10．（3分）正方形ABCD的边长AB=2，E为AB的中点，F为BC的中点，AF分别与DE、BD相交于点M，N，则MN的长为（　　） A． B． ﹣1 C． D．【分析】首先过F作FH⊥AD于H，交ED于O，于是得到FH=AB=2，根据勾股定理求得AF，根据平行线分线段成比例定理求得OH，由相似三角形的性质求得AM与AF的长，根据相似三角形的性质，求得AN的长，即可得到结论．【解答】解：过F作FH⊥AD于H，交ED于O，则FH=AB=2， ∵BF=FC，BC=AD=2， ∴BF=AH=1，FC=HD=1， 13 ∴AF= ==，∵OH∥AE， ∴ = = ，，∴OH= AE= ∴OF=FH﹣OH=2﹣ = ，∵AE∥FO， ∴△AME∽FMO， ∴ = = ，∴AM= AF= ∵AD∥BF，，∴△AND∽△FNB， ∴ = =2， ∴AN=2AF= ，∴MN=AN﹣AM= 故选：C． ﹣=．【点评】本题考查了相似三角形的判定与性质，矩形的性质，勾股定理，比例的性质，准确作出辅助线，求出AN与AM的长是解题的关键．　二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把最终结果直接填写在答题卡相应位置上） 11．（3分）“辽宁舰“最大排水量为67500吨，将67500用科学记数法表示为　6.75×104　．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：67500=6.75×104，故答案为：6.75×104． 14 【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤ |a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　12．（3分）分解因式：a3﹣2a2b+ab2=　a（a﹣b）2　．【分析】先提取公因式a，再对余下的多项式利用完全平方公式继续分解．【解答】解：a3﹣2a2b+ab2， =a（a2﹣2ab+b2）， =a（a﹣b）2．【点评】本题考查提公因式法分解因式和完全平方公式分解因式，熟记公式结构是解题的关键，分解因式一定要彻底．　13．（3分）已知正n边形的每一个内角为135°，则n=　8　．【分析】根据多边形的内角就可求得外角，根据多边形的外角和是360°，即可求得外角和中外角的个数，即多边形的边数．【解答】解：多边形的外角是：180﹣135=45°， ∴n= =8．【点评】任何任何多边形的外角和是360°，不随边数的变化而变化．根据这个性质把多边形的角的计算转化为外角的计算，可以使计算简化．　14．（3分）某厂一月份生产某机器100台，计划三月份生产160台．设二、三月份每月的平均增长率为x，根据题意列出的方程是　100（1+x）2=160　．【分析】设二，三月份每月平均增长率为x，根据一月份生产机器100台，三月份生产机器1 60台，可列出方程．【解答】解：设二，三月份每月平均增长率为x， 100（1+x）2=160．故答案为：100（1+x）2=160．【点评】本题考查理解题意的能力，本题是个增长率问题，发生了两次变化，先找出一月份的产量和三月份的产量，从而可列出方程．　15 15．（3分）如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=3，AB=5，OD⊥BC于点D，则 OD的长为　2　．【分析】先利用圆周角定理得到∠ACB=90°，则可根据勾股定理计算出AC=4，再根据垂径定理得到BD=CD，则可判断OD为△ABC的中位线，然后根据三角形中位线性质求解．【解答】解：∵AB是⊙O的直径， ∴∠ACB=90°， ∴AC= =4， ∵OD⊥BC， ∴BD=CD，而OB=OA， ∴OD为△ABC的中位线， ∴OD= AC= ×4=2．故答案为2．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理．　16．（3分）下面是“作一个30°角”的尺规作图过程．已知：平面内一点A．求作：∠A，使得∠A=30°．作图：如图，（1）作射线AB；（2）在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；（3）以C为圆心，OC为半径作弧，与⊙O交于点D，作射线AD，∠DAB即为所求的角．请回答：该尺规作图的依据是　 16 直径所对的圆周角的直角，等边三角形的时故内角为60°，直角三角形两锐角互余等　．【分析】连接OD、CD．只要证明△ODC是等边三角形即可解决问题；【解答】解：连接OD、CD．由作图可知：OD=OC=CD， ∴△ODC是等边三角形， ∴∠DCO=60°， ∵AC是⊙O直径， ∴∠ADC=90°， ∴∠DAB=90°﹣60°=30°． ∴作图的依据是：直径所对的圆周角的直角，等边三角形的时故内角为60°，直角三角形两锐角互余等，故答案为直径所对的圆周角的直角，等边三角形的时故内角为60°，直角三角形两锐角互余等．【点评】本题考查作图﹣复杂作图，圆的有关性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．　17．（3分）如图，在△ABC中，∠C=90°，AC=3，BC=4，点O是BC中点，将△ABC绕点O旋转得△A′B’C，则在旋转过程中点A、C′两点间的最大距离是　2+ 　． 17 【分析】连接OA，AC′，如图，易得OC=2，再利用勾股定理计算出OA= ，接着利用旋转的性质得OC′=OC=2，根据三角形三边的关系得到AC′≤OA+OC′（当且仅当点A、O、C′共线时，取等号），从而得到AC′的最大值．【解答】解：连接OA，AC′，如图， ∵点O是BC中点， ∴OC= BC=2，在Rt△AOC中，OA= =，∵△ABC绕点O旋转得△A′B’C′， ∴OC′=OC=2， ∵AC′≤OA+OC′（当且仅当点A、O、C′共线时，取等号）， ∴AC′的最大值为2+ 即在旋转过程中点A、C′两点间的最大距离是2+ 故答案为2+ ，．．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．　18．（3分）在平面直角坐标系xOy中，过点A（3，0）作垂直于x轴的直线AB，直线y=﹣x+b 与双曲线y= 交于点P（x1，y1），Q（x2，y2），与直线AB交于点R（x3，y3），若y1＞y2＞ 18 y3时，则b的取值范围是　2＜b＜　．【分析】根据y2大于y3，说明x=3时，﹣x+b＜，再根据y1大于y2，说明直线l和抛物线有两个交点，即可得出结论．【解答】解：如图，当x=3时，y2= ，y3=﹣3+b， ∵y3＜y2， ∴﹣3+b＜，∴b＜，∵y1＞y2， ∴直线l：y=﹣x+b①与双曲线y= ②有两个交点，联立①②化简得，x2﹣bx+1=0有两个不相等的实数根， ∴△=b2﹣4＞0， ∴b＜﹣2（舍）或b＞2， ∴2＜b＜，故答案为：2＜b＜．【点评】此题主要考查了反比例函数和一次函数的交点问题，一元二次方程根的判别式，熟练掌握一次函数和双曲线的性质是解本题的关键．　三、解答题（本大题共10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤） 19 19．（10分）（1）计算：| ﹣2|+20130﹣（﹣ ）﹣1+3tan30°；（2）解方程： ﹣3． =【分析】（1）原式利用绝对值的代数意义，零指数幂、负整数指数幂法则，以及特殊角的三角函数值计算即可求出值；（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：（1）原式=2﹣ +1+3+ =6；（2）去分母得：1=x﹣1﹣3x+6，解得：x=2，经检验x=2是增根，分式方程无解．【点评】此题考查了解分式方程，以及实数的运算，熟练掌握运算法则是解本题的关键．　20．（8分）解不等式组，并写出x的所有整数解．【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．【解答】解：解不等式①，得：x≥﹣ ，解不等式②，得：x＜3，则不等式组的解集为﹣ ≤x＜3， ∴不等式组的整数解为：﹣1、0、1、2．【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“ 同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．　21．（8分）“校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题： 20 （1）接受问卷调查的学生共有　60　人，扇形统计图中“了解”部分所对应扇形的圆心角为　90　度；（2）请补全条形统计；（3）若该中学共有学生1200人，估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数．【分析】（1）由基本了解的有30人，占50%，可求得接受问卷调查的学生数，继而求得扇形统计图中“了解”部分所对应扇形的圆心角；（2）由（1）可求得了解很少的人数，继而补全条形统计图；（3）利用样本估计总体的方法，即可求得答案．【解答】解：（1）接受问卷调查的学生共有30÷50%=60人，扇形统计图中“了解”部分所对应扇形的圆心角为360°× =90°，故答案为：60、90．（2）“了解很少”的人数为60﹣（15+30+5）=10人，补全图形如下： 21 （3）估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数为1200× =900人．【点评】此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图．关键是根据列表法或树状图法求概率以及条形统计图与扇形统计图．　22．（8分）四张扑克牌的点数分别是2，3，4，8，除点数不同外，其余都相同，将它们洗匀后背面朝上放在桌上．（1）从中随机抽取一张牌，求这张牌的点数是偶数的概率；（2）随机抽取一张牌不放回，接着再抽取一张牌，求这两张牌的点数都是偶数的概率．【分析】（1）利用数字2，3，4，8中一共有3个偶数，总数为4，即可得出点数偶数的概率；（2）列表得出所有情况，让点数都是偶数的情况数除以总情况数即为所求的概率．【解答】解：（1）因为共有4张牌，其中点数是偶数的有3张，所以这张牌的点数是偶数的概率是；（2）列表如下： 2348234（2，3）（2，4）（3，4）（2，8）（3，8）（4，8）（3，2）（4，2）（4，3） 22 8（8，2）（8，3）（8，4）从上面的表格可以看出，总共有12种结果，每种结果出现的可能性相同，其中恰好两张牌的点数都是偶数有6种，所以这两张牌的点数都是偶数的概率为 = ．【点评】此题主要考查了列表法求概率，列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适用于两步或两步以上完成的事件；解题时还要注意是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．　23．（8分）如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60° 方向行驶12千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地的距离．（结果保留根号）【分析】作BH⊥AC于H，根据正弦的定义求出BH，根据余弦的定义计算即可．【解答】解：作BH⊥AC于H，由题意得，∠CBH=45°，∠BAH=60°，在Rt△BAH中，BH=AB×sin∠BAH=6 在Rt△BCH中，∠CBH=45°，，∴BC= =6 （千米），答：B，C两地的距离为6 千米． 23 【点评】本题考查的是解直角三角形的应用﹣方向角问题，掌握锐角三角函数的定义、正确标出方向角是解题的关键．　24．（8分）如图，▱ABCD中，点E是BC的中点，连接AE并延长交DC延长线于点F．（1）求证：CF=AB；（2）连接BD、BF，当∠BCD=90°时，求证：BD=BF．【分析】（1）欲证明AB=CF，只要证明△AEB≌△FEC即可；（2）想办法证明AC=BD，BF=AC即可解决问题；【解答】证明：（1）∵四边形ABCD是平行四边形， ∴AB∥DF， ∴∠BAE=∠CFE ∵AE=EF，∠AEB=∠CEF， ∴△AEB≌△FEC， ∴AB=CF．（2）连接AC． ∵四边形ABCD是平行四边形，∠BCD=90°， ∴四边形ABCD是矩形， ∴BD=AC， ∵AB=CF，AB∥CF， ∴四边形ACFB是平行四边形， ∴BF=AC， 24 ∴BD=BF．【点评】本题考查平行四边形的判定和性质、矩形的判定和性质、全等三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．　25．（8分）一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：（1）慢车的速度为　80　km/h，快车的速度为　120　km/h；（2）解释图中点C的实际意义并求出点C的坐标；（3）求当x为多少时，两车之间的距离为500km．【分析】（1）由图象可知，两车同时出发．等量关系有两个：3.6×（慢车的速度+快车的速度）=720，（9﹣3.6）×慢车的速度=3.6×快车的速度，设慢车的速度为akm/h，快车的速度为bkm/h，依此列出方程组，求解即可；（2）点C表示快车到达乙地，然后求出快车行驶完全程的时间从而求出点C的横坐标，再求出相遇后两辆车行驶的路程得到点C的纵坐标，从而得解；（3）分相遇前相距500km和相遇后相遇500km两种情况求解即可．【解答】解：（1）设慢车的速度为akm/h，快车的速度为bkm/h，根据题意，得，解得，故答案为80，120；（2）图中点C的实际意义是：快车到达乙地； ∵快车走完全程所需时间为720÷120=6（h）， ∴点C的横坐标为6，纵坐标为（80+120）×（6﹣3.6）=480， 25 即点C（6，480）；（3）由题意，可知两车行驶的过程中有2次两车之间的距离为500km．即相遇前：（80+120）x=720﹣500，解得x=1.1，相遇后：∵点C（6，480）， ∴慢车行驶20km两车之间的距离为500km， ∵慢车行驶20km需要的时间是 =0.25（h）， ∴x=6+0.25=6.25（h），故x=1.1 h或6.25 h，两车之间的距离为500km．【点评】本题考查了一次函数的应用，主要利用了路程、时间、速度三者之间的关系，（3 ）要分相遇前与相遇后两种情况讨论，这也是本题容易出错的地方．　26．（12分）如图，△ABC中，AB=6cm，AC=4 cm，BC=2 cm，点P以1cm/s的速度从点B 出发沿边BA→AC运动到点C停止，运动时间为t s，点Q是线段BP的中点．（1）若CP⊥AB时，求t的值；（2）若△BCQ是直角三角形时，求t的值；（3）设△CPQ的面积为S，求S与t的关系式，并写出t的取值范围．【分析】（1）如图1中，作CH⊥AB于H．设BH=x，利用勾股定理构建方程求出x，当点P与H 重合时，CP⊥AB，此时t=2；（2）分两种情形求解即可解决问题；（3）分两种情形：①如图4中，当0＜t≤6时，S= ×PQ×CH；②如图5中，当6＜t＜6+4 时，作BG⊥AC于G，QM⊥AC于M．求出QM即可解决问题；【解答】解：（1）如图1中，作CH⊥AB于H．设BH=x， 26 ∵CH⊥AB， ∴∠CHB=∠CHB=90°， ∴AC2﹣AH2=BC2﹣BH2， ∴（4 ）2﹣（6﹣x）2=（2 ）2﹣x2，解得x=2， ∴当点P与H重合时，CP⊥AB，此时t=2．（2）如图2中，当点Q与H重合时，BP=2BQ=4，此时t=4．如图3中，当CP=CB=2 时，CQ⊥PB，此时t=6+（4 ﹣2 ）=6+4 ﹣2 ．（3）①如图4中，当0＜t≤6时，S= ×PQ×CH= × t×4=t． 27 ②如图5中，当6＜t＜6+4 时，作BG⊥AC于G，QM⊥AC于M．易知BG=AG=3 ，CG= ．MQ= BG= ．∴S= ×PC×QM= • 综上所述，s= •（6+4 ﹣t）= +6﹣ t．．【点评】本题考查三角形综合题、勾股定理、等腰三角形的判定和性质、三角形的面积等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．　27．（12分）已知，正方形ABCD，A（0，﹣4），B（l，﹣4），C（1，﹣5），D（0，﹣5 ），抛物线y=x2+mx﹣2m﹣4（m为常数），顶点为M．（1）抛物线经过定点坐标是　（2，0）　，顶点M的坐标（用m的代数式表示）是　（﹣ ，﹣ ）　；（2）若抛物线y=x2+mx﹣2m﹣4（m为常数）与正方形ABCD的边有交点，求m的取值范围；（3）若∠ABM=45°时，求m的值． 28 【分析】（1）判断函数图象过定点时，可以分析代入的x值使得含m的同类项合并后为系数为零．（2）由（1）中用m表示的顶点坐标，可以得到在m变化时，抛物线顶点M抛物线在y=﹣x2+4 x﹣4上运动，分析该函数图象和正方形ABCD的顶点位置关系可以解答本题；（3）由已知点M在过点B且与AB夹角为45°角的直线与抛物线在y=﹣x2+4x﹣4的交点上，则问题可解．【解答】解：（1）y=x2+mx﹣2m﹣4=（x2﹣4）+m（x﹣2）=（x﹣2）（x+2+m），当x=2时，y=0， ∴抛物线经过定点坐标是（2，0）． ∵抛物线的解析式为y=x2+mx﹣2m﹣4， ∴顶点M的对称轴为直线x=﹣ =﹣ 当x═﹣ 时，y=（﹣ ）2+m•（﹣ ）﹣2m﹣4=﹣ 故答案为：（2，0）；（﹣ ，﹣ （2）设x=﹣ ，y=﹣ ）．则m=﹣2x，带入y=﹣ ，﹣ ．整理得 29 y=﹣x2+4x﹣4 即抛物线的顶点在抛物线y=﹣x2+4x﹣4上运动．其对称轴为直线x=2，当抛物线顶点直线x=2右侧时即m＜﹣4时，抛物线y=x2+mx﹣2m﹣4与正方形ABCD无交点．当m＞﹣4时，观察抛物线的顶点所在抛物线y=﹣x2+4x﹣4恰好过点A（0，﹣4），此时m=0 当抛物线y=x2+mx﹣2m﹣4过点C（1，﹣5）时 ﹣5=1+m﹣2m﹣4，得m=2 ∴抛物线y=x2+mx﹣2m﹣4（m为常数）与正方形ABCD的边有交点时m的范围为： 0≤m≤2 （3）由（2）抛物线顶点M在抛物线y=﹣x2+4x﹣4上运动当点M在线段AB上方时，过点B且使∠ABM=45°的直线解析式为y=﹣x﹣3 联立方程﹣x2+4x﹣4=﹣x﹣3 求交点横坐标的x1= （舍去） x2= m=﹣5+ 当点M在线段AB下方时过点B且使∠ABM=45°的直线解析式为y=x﹣5 联立方程﹣x2+4x﹣4=x﹣5 求交点横坐标为x1= （舍去）x2= m=﹣3 ∴m的值为﹣5+ 或﹣3 【点评】本题考查含有字母参数的二次函数图象及其性质，解答过程中注意数形结合，关注m的变化过程中，抛物线的变化趋势．　28．（14分）如图，⊙O的直径AB=26，P是AB上（不与点A、B重合）的任一点，点C、D为⊙ O上的两点，若∠APD=∠BPC，则称∠CPD为直径AB的“回旋角”．（1）若∠BPC=∠DPC=60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；（2）若的长为 π，求“回旋角”∠CPD的度数；（3）若直径AB的“回旋角”为120°，且△PCD的周长为24+13 ，直接写出AP的长． 30 【分析】（1）利用平角求出∠APD=60°，即可得出结论；（2）先求出∠COD=45°，进而判断出点D，P，E在同一条直线上，求出∠CED，即可得出结论；（3）①当点P在半径OA上时，利用（2）的方法求出∠CFD=60°，∠COD=120°，利用三角函数求出CD，进而求出DF，再用勾股定理求出OH，即可求出OP即可得出结论； ②当点P在半径OB上时，同①方法求出BP=3，即可得出结论．【解答】解：∠CPD是直径AB的“回旋角”，理由：∵∠CPD=∠BPC=60°， ∴∠APD=180°﹣∠CPD﹣∠BPC=180°﹣60°﹣60°=60°， ∴∠BPC=∠APD， ∴∠CPD是直径AB的“回旋角”；（2）如图1，∵AB=26， ∴OC=OD=OA=13，设∠COD=n°， ∵∴的长为 π，，∴n=45， ∴∠COD=45°，作CE⊥AB交⊙O于E，连接PE， ∴∠BPC=∠OPE， ∵∠CPD为直径AB的“回旋角”， ∴∠APD=∠BPC， ∴∠OPE=∠APD， ∵∠APD+∠CPD+∠BPC=180°， 31 ∴∠OPE+∠CPD+∠BPC=180°， ∴点D，P，E三点共线， ∴∠CED= ∠COD=22.5°， ∴∠OPE=90°﹣22.5°=67.5°， ∴∠APD=∠BPC=67.5°， ∴∠CPD=45°，即：“回旋角”∠CPD的度数为45°，（3）①当点P在半径OA上时，如图2，过点C作CF⊥AB交⊙O于F，连接PF， ∴PF=PC，同（2）的方法得，点D，P，F在同一条直线上， ∵直径AB的“回旋角”为120°， ∴∠APD=∠BPC=30°， ∴∠CPF=60°， ∴△PCF是等边三角形， ∴∠CFD=60°，连接OC，OD， ∴∠COD=120°，过点O作OG⊥CD于G， ∴CD=2DG，∠DOG= ∠COD=60°， ∴DG=ODsin∠DOG=13×sin60°= ∴CD=13 ，，∵△PCD的周长为24+13 ∴PD+PC=24，，∵PC=PF， ∴PD+PF=DF=24，过O作OH⊥DF于H， ∴DH= DF=12， 32 在Rt△OHD中，OH= =5，在Rt△OHP中，∠OPH=30°， ∴OP=10， ∴AP=OA﹣OP=3； ②当点P在半径OB上时，同①的方法得，BP=3， ∴AP=AB﹣BP=23，即：满足条件的AP的长为3或23．【点评】此题是圆的综合题，主要考查了垂径定理，三点共线，锐角三角函数，勾股定理，新定义，正确作出辅助线是解本题的关键．　33