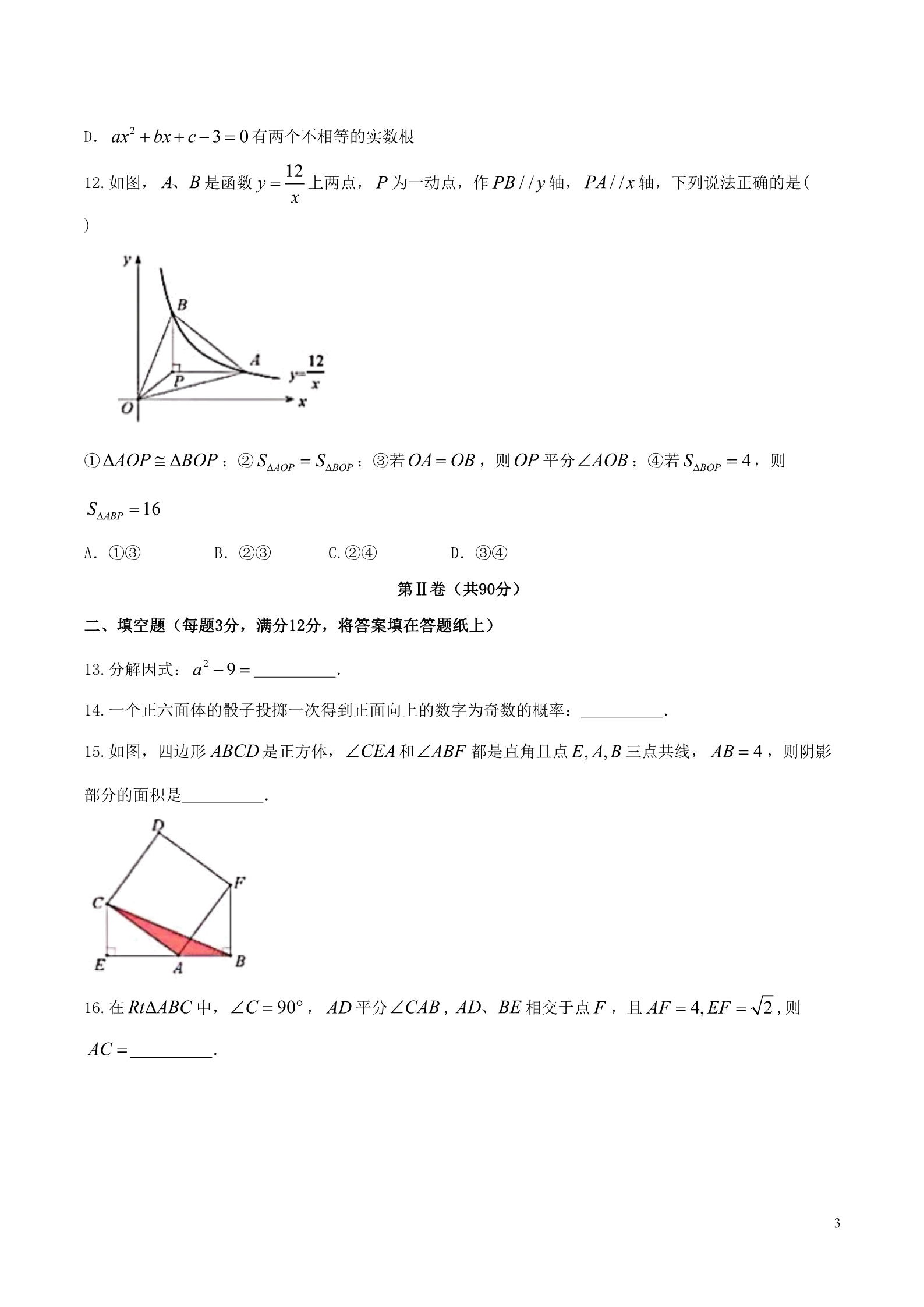
广东省深圳市2018年中考数学真题试题（含答案）

广东省深圳市2018年中考数学真题试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.6的相反数是( A． 6 )1616B． C． D．6 2.260000000用科学计数法表示为( )A． 0.26109 B． 2.6108 C． 2.6109 D． 26107 3.图中立体图形的主视图是( )A． B． C． D． 4.观察下列图形，是中心对称图形的是( )A． B． C. D． 5.下列数据： 75,80,85,85,85 ，则这组数据的众数和极差是( )A．85,10 B．85,5 C.80,85 D．80,10 6.下列运算正确的是( A． a2 a3  a6 )B．3a  a  2a C. a8  a4  a2 D． a  b  ab 17.把函数 y  x 向上平移3个单位，下列在该平移后的直线上的点是( A． 2,2 B． 2,3 C. 2,4 D． (2,5) c,d 所截，且 a / /b ，则下列结论中正确的是( )8.如图，直线 a,b 被)A． 1   2 B．   3  4 C.2  4 180 D． 1 4 180 9.某旅店一共70个房间，大房间每间住8个人，小房间每间住6个人，一共480个学生刚好住满，设大房间有x个，小房间有 y个.下列方程正确的是( )x  y  70 x  y  70 x  y  480 x  y  480 A． B． C. D． 8x  6y  480 6x 8y  480 6x 8y  70 8x  6y  70 10.如图，一把直尺， 60的直角三角板和光盘如图摆放，径是( A为60角与直尺交点， AB  3,则光盘的直 )A．3 B．3 3 C. 6D． 6 3 11.二次函数 y  ax2  bx  c(a  0)的图像如图所示，下列结论正确是( )A． abc  0 B． 2a  b  0 C.3a  c  0 2D． ax2  bx  c 3  0 有两个不相等的实数根 12 12.如图， A、B 是函数 y  上两点， P为一动点，作 PB / / y 轴， PA / /x 轴，下列说法正确的是( x)①AOP  BOP ；② SAOP  SBOP ；③若OA  OB ，则OP 平分 AOB ；④若 SBOP  4，则 SABP 16 A．①③ B．②③ C.②④ D．③④ 第Ⅱ卷（共90分）二、填空题（每题3分，满分12分，将答案填在答题纸上） 13.分解因式： a2 9  14.一个正六面体的骰子投掷一次得到正面向上的数字为奇数的概率： 15.如图，四边形 ABCD 是正方体， CEA ABF 都是直角且点 E, A, B 三点共线， AB  4 ，则阴影部分的面积是．．和．16.在 RtABC 中， C  90° AC  ，AD 平分 CAB F , ，且 AF  4, EF  2 ,则 AD、BE 相交于点．3三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） -1 1  17. 计算：  2sin 45°+2 +(2018- )0 .  2  xx2  2x 1 x2 1 18. 先化简，再求值： 1  ，其中 x  2 .x 1 19.某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：频数 40 频率 0.4 a体育科技艺术其它 25 0.15 0.2 b20 请根据上图完成下面题目： (1)总人数为__________人， a __________,b  __________. (2)请你补全条形统计图. (3)若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？ 20.已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在 CFE 中，CF  6,CE 12 为圆心，以任意 FCE  45° ，以点C ,41长为半径作 AD ，再分别以点 (1)求证：四边形 ACDB A和点 D为圆心，大于 AD 长为半径做弧，交 EF 于点 B, AB / /CD .2为FEC 的亲密菱形； (2)求四边形 ACDB 的面积. 21. 某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贯2元. (1)第一批饮料进货单价多少元？ (2)若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？10 22. 如图在 O 中， BC  2, AB  AC ，点 D为AC 上的动点，且 cos B  .10 (1)求 AB 的长度； (2)求 AD AE 的值； (3)过 A点作 AH  BD ，求证： BH  CD  DH .21235223.已知顶点为 A抛物线 y  a x  2经过点 B  ,2 ，点 C,2 .2(1)求抛物线的解析式； yE F (2)如图1，直线 AB 与轴相交于点M , y 轴相交于点，抛物线与轴相交于点，在直线AB 上有一 x5点P，若 OPM  MAF ，求 POE 的面积；图1 (3)如图2，点 QN是折线 A B C 上一点，过点 Q作QN / / y 轴，过点 E作EN / /x 轴，直线QN 与直线 EN 相交于点的坐标. ，连接QE ，将 QEN 沿QE 翻折得到 QEN1 ，若点 N1 落在轴上，请直接写出点 xQ图2 6参考答案一、选择题 1-5: ABBDA 二、填空题 6-10:BDBAD 11、12：CB 128 10 513. a  3 a 3 14. 15. 816.  三、解答题 17.3 x  x 1 (x 1)(x 1) x 1 118.解：原式 (x 1)2 x 1 13把x  2 代入得：原式 19.解：(1)0.4  40 100 （人） a  25100  0.25 ，b 1000.15 15 （人）， (2)如图： 7(3)6000.15  90（人） 20.解：(1)证明：由已知得： AC  CD AB  DB ,由已知尺规作图痕迹得： BC 则： ACB  DCB 是FCE 的角平分线又 AB / /CD ABC  DCB ACB  ABC  AC  AB 又 AC  CD, AB  DB  AC  CD  DB  BA 四边形 ACDB 是菱形 ACD ∴四边形 ACDB 与FCE 中的 FCE 重合，它的对角 ABD 顶点在 EF FEC 的亲密菱形上为(2)解：设菱形 ACDB 的边长为 x可证： EAB∽FCE FA AB x6  x 6则： ,即 FC CE 12 解得： x  4 过在A点作 AH  CD H于点 RtACH 中， ACH  45° AC  AH   2 2 2∴四边形 ACDB 的面积为： 42 2=8 2 81600 6000 21.解:（1）设第一批饮料进货单价为 x元，则：3 xx  2 解得： x  8 经检验： x  8是分式方程的解答：第一批饮料进货单价为8元. (2)设销售单价为 m元，则： (m 8)200  (m 10)600 1200 化简得： 2(m 8)  6(m 10) 12 解得： m 11 答：销售单价至少为11元. 22.解：(1)作 AM  BC  AB  AC, AM  BC, BC  2 1BM  CM  BC 1 2BM AB 10 cos B  ，在 RtAMB 中， BM 1 10 10  AB  BM cos B 1  10 .10 (2)连接 DC  AB  AC ACB  ABC ∵四边形 ABCD 内接于圆 O，ADC  ABC 180 ，ACE  ACB 180 ADC  ACE ，9CAE 公共 EAC∽CAD AC AE AD AC 2 AD AE  AC2  10 10 .（3）在 BD 上取一点 N，使得 BN  CD AB  AC 3  1 BN  CD 在ABN 和ACD 中ABN  ACD(SAS)  AN  AD  AN  AD, AH  BD NH  HD BN  CD, NH  HD BN  NH  CD  HD  BH .10 231223.解：(1)把点 B  ,2 代入 y  a x  2，解得： a 1 ，22127∴抛物线的解析式为： y  x   2 或y  x2  x  ；4(2)设直线 AB 解析式为： y  kx  b ，代入点 A, B 的坐标得： 12  k  b k  2 b  1 23，解得：，∴直线 AB 的解析式为： y  2x 1 ，2  k  b 2741易求 E 0,1 ,F 0, ,M  ,0 ,2若OPM  MAF ,OP OE 13443则当OP / /AF 时， OPE∽EAE ,,FA FE 22  6  2  44312745OP  FA  ,335设点 P t,2t 1 ，则： t2  (2t 1)2  322解得t1   ，t2   ，15 32由对称性知；当t1  时，也满足 OPM  MAF ,15 22t1   ，t2  都满足条件 15 3111POE 的面积，POE 的面积为或.  OE  l 215 311