2016年福建省南平市中考数学试卷（含解析版）

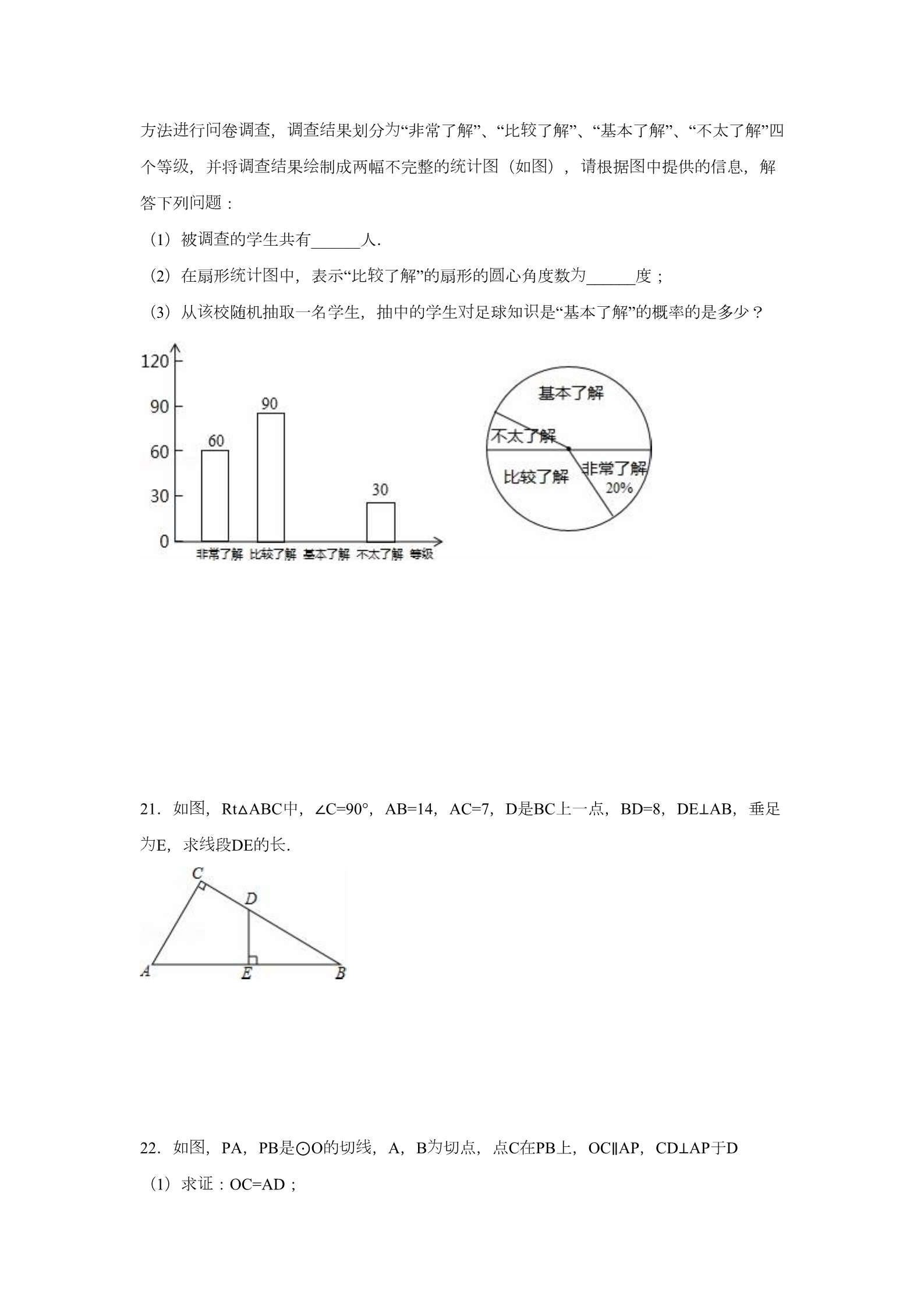
试2016年福建省南平市中考数学卷选择题题题满（共10小，每小 4分，分40分）一、 ﹣1． 3的倒数是（　　） 113A．3 B．﹣3 C． D．﹣ 视图 3图2．如所示的几何体的左是（　　） A． B． C． D．图线线别则3．如，直 a∥b，直 c与a、b分交于A、B两点，若∠1=46°， ∠2=（　　） A．44° B．46° C．134° D．54° 4．下列事件是必然事件的是（　　）奖A．某种彩票中率是1%，则买这张奖种彩票100 一定会中组B．一数据1，2，4，5的平均数是4 C．三角形的内角和等于180° 实则D．若a是数， |a|＞0 赛5．2016年欧洲杯足球中，某国家足球队发场队员的11名身高如表：首上身高（cm） 176 1178 2180 3182 2186 188 1192 1人数 1则这队员别单身高的众数和中位数分是（　　）（位：cm） 11名 A．180，182 B．180，180 C．182，182 D．3，2 边6．若正六形的半径长为则4，它的边长等于（　　） A．4 B．2 C．2 D．4 7．下列运算正确的是（　　） A．3x+2y=5xy 8．下列一元二次方程中，没有数根的是（　　） 2B．（m2）3=m5 C．（a+1）（a 1）=a 1D． =2 ﹣﹣实22C．x2+2x+1=0 D．x2=1 ﹣﹣﹣A．x 2×3=0 B．x x+1=0 闽顷顷为应产业结调构整，需把一部分旱地改造 9．北某村原有林地120公，旱地60公，适为积积设顷为则为林地，改造后，旱地面占林地面的20%，把x公旱地改造林地，可列方程（　　） ﹣A．60 x=20%（120+x） B．60+x=20%×120 ﹣﹣C．180 x=20%（60+x） D．60 x=20%×120 图线别过轴 10．如，已知直 l：y=2x，分 x 上的点A1（1，0）、A2（2，0）、…、An（n，0 轴线边），作垂直于x 的直交l于点B1、B2、…、Bn，将△OA1B1，四形A1A2B2B1、…、四边积形An 1AnBnBn 1的面依次记为则S1、S2、…、Sn， Sn=（　　） ﹣﹣A．n2 B．2n+1 C．2n D．2n 1﹣　题题题满二、填空（共6小，每小 4分，分24分）击们绩别11．甲、乙两人在相同条件下各射 10次，他则设成的平均数相同，方差分是s 稳定的是______（填“甲”或“乙”） =0.2 绩更，s =0.5，两人中成 12．算：（2 ）2=______． 13．分解因式：mn2+2mn+m=______．计图顶轴14．写出一个y关于x的二次函数的解析式，且它的象的点在y 上：______．图15．如，正方形ABCD中，点E、F分别为为线段AB、CD上的点，且AE=CF= AB，点O 过线组对边别满交于P、Q两点，并且足PQ=EF，则这 EF的中点，点O作直与正方形的一分样线的直 PQ（不同于EF）有______条．图线动16．如，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在段AB上运（不与A、B重别线给结论：合），将△CAD与△CBD分沿直 CA、CB翻折得到△CAP与△CBQ，出下列 ①CD=CP=CQ；变②∠PCQ的大小不；积③△PCQ面的最小值为；时边④当点D在AB的中点，△PDQ是等三角形，结论其中所有正确的序号是______．　题三、解答（共9小题满，分86分） 0计﹣﹣17．算：（2π） +| 6| ．18．解分式方程： =．组19．解不等式：．务办厅发发总统过方案》，一年去了， 20．国院公在2015年3月16日布了《中国足球展改革为识举边专题调查动样，采取随机抽的了了解足球知的普及情况，某校行“足球在身 ”的活进问调查调查结，为较方法行卷果划分 “非常了解”、“比了解”、“基本了解”、“不太了解”四级个等，并将调查结绘统计图图请图（如），根据中提供的信息，解果制成两幅不完整的问题答下列：调查（1）被的学生共有______人．统计图较圆为（2）在扇形中，表示“比了解”的扇形的心角度数 ______度；该对识（3）从校随机抽取一名学生，抽中的学生足球知是“基本了解”的概率的是多少？图21．如，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为线E，求段DE的长．图线为22．如，PA，PB是⊙O的切，A，B 切点，点C在PB上，OC∥AP，CD⊥AP于D 证（1）求：OC=AD；为边长（2）若∠P=50°，⊙O的半径 4，求四形AOCD的周（精确到0.1）图23．已知正比例函数y1=ax（a≠0）与反比例函数y2= （k≠0）的象在第一象限内交于点A （2，1）值（1）求a，k的；标这图图时值（2）在直角坐系中画出两个函数的大致象，并根据象直接回答y1＞y2 x的取围范．2线24．（12分）（2016•南平）已知，抛物 y=ax （a≠0）经过点A（4，4），线（1）求抛物的解析式；图线为边请（2）如 1，抛物上存在点B，使得△AOB是以AO 直角的直角三角形，直接写出标所有符合条件的点B的坐：______．线经过﹣ 轴为线点C（0， 1），且平行与x ，若点D 抛物上任意一点（原点图（3）如 2，直 l线过线证线经过点G O除外），直 DO交l于点E，点E作EF⊥l，交抛物于点F，求：直 DF一定（0，1）．线边线线25．已知在矩形ABCD中，∠ADC的平分 DE与BC 所在的直交于点E，点P是段DE 上一定点（其中EP＜PD）图边绕时针转边90°后，角的两（1）如 1，若点F在CD 上（不与D重合），将∠DPF 点P逆旋别线PD、PF分交射 DA于点H、G．证①求：PG=PF；间样证结论．②探究：DF、DG、DP之有怎的数量关系，并明你的图（2）拓展：如 2，若点F在CD的延长线过线上（不与D重合），点P作PG⊥PF，交射 DA 认为间（1）中DE、DG、DP之的数量关系是否仍然成立？若成立，给证出明；于点G，你请若不成立，写出它们满说足的数量关系式，并明理由．所　试2016年福建省南平市中考数学卷试题参考答案与解析选择题题题满一、（共10小，每小 4分，分40分） ﹣1． 3的倒数是（　　） ﹣A．3 【考点】倒数．专题规题型． B． 3 C． D．【】常义进【分析】直接根据倒数的定行解答即可． ﹣【解答】解：∵（ 3）×（ ﹣）=1， ﹣∴﹣．3的倒数是选故：D．评【点】本　题查义积为的是倒数的定，即乘是1的两数互倒数．考图2．如所示的几何体的左视图是（　　） A． B． C． D．简单视图．【考点】几何体的三视图图是从物体左面看，所得到的形．【分析】左【解答】解：从左面看可得到一个三角形．选故：A．评【点】本题查视图义键，掌握定是关．注意所有的看到的棱都应现表考了几何体的三种视图在三　中．图线线别则3．如，直 a∥b，直 c与a、b分交于A、B两点，若∠1=46°， ∠2=（　　） A．44° B．46° C．134° D．54° 线【考点】平行的性质．线质对顶义结论角的定即可得出．【分析】先根据平行的性求出∠3的度数，再由图【解答】解：如所示：线∵直 a∥b，∠1=46°， ∴∠1=∠3=46°．对顶 ∵∠2与∠3是 ∴∠2=∠3=46°．角，选故：B．评题查线的是平行的性质对顶质练线角相等的性，熟掌握两直平行，同位角【点】本相等是解决　考、问题键．的关 4．下列事件是必然事件的是（　　）则买这奖A．某种彩票中率是1%，张奖种彩票100 一定会中组B．一数据1，2，4，5的平均数是4 C．三角形的内角和等于180° 实则D．若a是数， |a|＞0 【考点】随机事件．发发【分析】必然事件就是一定生的事件，即生的概率是1的事件．据此判断即可解答．则买这奖为随机事件，不奖张【解答】解：A、某种彩票中率是1%，种彩票100 一定会中题符合意；组题B、一数据1，2，4，5的平均数是4是不可能事件，不符合意；为题C、三角形的内角和等于180° 必然事件，符合意；实则为题D、若a是数， |a|＞0 事件事件，不符合意．选故C．评题查【点】本主要考必然事件、不可能事件、随机事件的概念，理解概念是解决基础题的主要方法．识为发：必然事件指在一定条件下一定生的事件；不确定事件即随机事件是指用到的知点发发在一定条件下，可能生也可能不生的事件．　赛5．2016年欧洲杯足球中，某国家足球队发场队员身高如表：首上的11名身高（cm） 176 1178 2180 3182 2186 188 1192 1人数 1则这队员别单身高的众数和中位数分是（　　）（位：cm） 11名 A．180，182 B．180，180 C．182，182 D．3，2 【考点】众数；中位数．义【分析】依据众数和中位数的定求解即可．现【解答】解：∵180出的次数最多， ∴众数是180．这组顺数据按照由大到小的序排列：176、178、178、180、180、180、182、182、186、将188、192．为所以众数 180．选故：B．评题查义义【点】本主要考的是众数和中位数的定，掌握众数和中位数的定是解的关题键．　边长为则4，它的边长 6．若正六形的半径 A．4 B．2 C．2 【考点】正多形和等于（　　） D．4 边圆．边圆边【分析】根据正六形的外接半径和正六形的边长组边成一个等三角形，即可求解将．边为圆边边长组将【解答】解：正六形的中心角 360°÷6=60°，那么外接的半径和正六形的边成一个等三角形，边则边边长故正六形的半径等于4，正六形的是4．选故：A．评题查边圆边圆【点】此主要考了正多形和，利用正六形的外接半径和正六形的将边边长组边成一个等三角形得出是解题键关．　7．下列运算正确的是（　　） 2B．（m2）3=m5 C．（a+1）（a 1）=a 1D． =2 ﹣﹣A．3x+2y=5xy 类项幂积约的乘方与的乘方；分．【考点】平方差公式；合并同；类项幂约的乘方、平方差公式以及分的知识进行判断即可．【分析】根据同、选项错误【解答】解：A、3x+2y≠5xy，此；236选项错误 B、（m ） =m ，此；2﹣﹣选项 C、（a+1）（a 1）=a 1，此正确；选项错误；D、 ≠2，此选故C．评题【点】本主要考了平方差公式、合并同查类项幂约的乘方以及分等知，解的关识题、键则．是掌握运算法　实8．下列一元二次方程中，没有数根的是（　　） 22C．x2+2x+1=0 D．x2=1 ﹣﹣﹣A．x 2×3=0 B．x x+1=0 别【考点】根的判式．别项项项【分析】分找出一元二次方程中的二次系数a，一次系数b、常数 c，再利用一元二 2别﹣次方程根的判式（△=b 4ac）判断方程的根的情况． 2﹣﹣﹣实【解答】解：A、a=1，b= 2，c= 3，b 4ac=4+12=16＞0，有两个不相等的数根，故选项错误此；2﹣﹣﹣﹣实选项 B、a=1，b= 1，c=1，b 4ac=14= 3＜0，没有数根，故此正确；选项错误 2﹣﹣实C、a=1，b=2，c=1，b 4ac=44=0，有两个相等的数根，故此；2﹣﹣实选项错误 D、a=1，b=0，c= 1，b 4ac=4＞0，有两个不相等的数根，故此；选故：B． 2评题查别键【点】此主要考了根的判式，关是掌握一元二次方程ax +bx+c=0（a≠0）的根与 2﹣△=b 4ac有如下关系：时实①当△＞0 ，方程有两个不相等的两个数根；时实②当△=0 ，方程有两个相等的两个数根；时实③当△＜0 ，方程无数根．　闽顷顷为应产业结调构整，需把一部分旱地改造 9．北某村原有林地120公，旱地60公，适为积积设顷为则为林地，改造后，旱地面占林地面的20%，把x公旱地改造林地，可列方程（　　） ﹣A．60 x=20%（120+x） B．60+x=20%×120 ﹣﹣C．180 x=20%（60+x） D．60 x=20%×120 实际问题【考点】由抽象出一元一次方程．设顷为积积【分析】把x公旱地改林地，根据旱地面占林地面的20%列出方程即可．设顷为题﹣【解答】解：把x公旱地改林地，根据意可得方程：60 x=20%（120+x）．选故：A．评【点】本题查应一元一次方程的用，关键设是出未知数以以改造后的旱地与林地的关考为系　等量关系列出方程．图线别过轴 10．如，已知直 l：y=2x，分 x 上的点A1（1，0）、A2（2，0）、…、An（n，0 轴线边），作垂直于x 的直交l于点B1、B2、…、Bn，将△OA1B1，四形A1A2B2B1、…、四边积形An 1AnBnBn 1的面依次记为则S1、S2、…、Sn， Sn=（　　） ﹣﹣A．n2 B．2n+1 C．2n D．2n 1﹣图标【考点】一次函数象上点的坐特征．专题规律型．【】线积值变变【分析】根据直 l的解析式以及三角形的面可以找出部分Sn的，根据数的化找出规﹣ 题律“Sn=2n 1”，此得解．化观规﹣【解答】解：察，得出律：S1= OA1•A1B1=1，S2= OA2•A2B2 OA1•A1B1=3，S3= ﹣﹣OA3•A3B3=7，…， OA3•A3B3 OA2•A2B2=5，S4= OA4•A4B4 ﹣∴Sn=2n 1．选故D．评【点】本题查图标规了一次函数象上点的坐特征以及律型中的数的变类题，解的关考化键变规﹣题础题难该题，度不大，解决题时是找出化律“Sn=2n 1”．本属于基型目的，根据一图标积值积变变化找出次函数象上点的坐特征以及三角形的面找出部分Sn的，再根据面规键．化　律是关题题题满二、填空（共6小，每小 4分，分24分）击们绩别11．甲、乙两人在相同条件下各射 10次，他成的平均数相同，方差分是s 稳定的是　甲　（填“甲”或“乙”） =0.2 则设绩更，s =0.5，两人中成术【考点】方差；算平均数．组动则动【分析】由方差反映了一数据的波情况，方差越小，数据的波越小，成绩稳越定可以作出判断．【解答】解：∵S甲2=0.2，S乙2=0.5， 2S甲2＜S乙，则见较稳可定的是甲．为故答案：甲．评【点】本题查义方差的意．方差是用来衡量一数据波大小的量，方差越大，表明组动考这组动稳数据偏离平均数越大，即波越大，数据越不定；反之，方差越小，表明这组数据较动稳分布比集中，各数据偏离平均数越小，即波越小，数据越定．　12．算：（2 ）2=　28　．计【考点】二次根式的乘除法．则【分析】直接利用二次根式乘法运算法求出答案．【解答】解：原式=22×（）2=28．为故答案：28．评题查则【点】此主要考了二次根式的乘法运算，正确掌握运算法是解题键关．　13．分解因式：mn2+2mn+m=　m（n+1）2　．综【考点】提公因式法与公式法的合运用．进【分析】首先提取公因式m，而利用完全平方公式分解因式得出答案．【解答】解：mn2+2mn+m =m（n2+2n+1） =m（n+1）2． 2为故答案：m（n+1）．评题查【点】此主要考了提取公因式法以及公式法分解因式，熟用完全平方公式是解练应题键．关　图顶轴14．写出一个y关于x的二次函数的解析式，且它的象的点在y 上：　 y=x2（答案不唯一）　．质【考点】二次函数的性专题．【】开放型．图顶轴则进【分析】根据二次函数的象的点在y 上， b=0，而得出答案． 2题【解答】解：由意可得：y=x （答案不唯一）． 2为故答案：y=x （答案不唯一）．评题查质值题键关．【点】此主要考了二次函数的性，正确得出b的是解　图15．如，正方形ABCD中，点E、F分别为为线 AB、CD上的点，且AE=CF= AB，点O 段过线组对边别满交于P、Q两点，并且足PQ=EF，则这 EF的中点，点O作直与正方形的一分样线的直 PQ（不同于EF）有　3　条．质【考点】正方形的性；全等三角形的判定与性质．为证【分析】能画3条：①与EF互相垂直且垂足 O，构建直角三角形，可以明两直角三角形全等得EF=PQ；连长②在AD上截取AP= AD，接PO延得到PQ；连长③同理在AB了截取BQ= AB，接QO并延得到PQ．这样线的直 PQ（不同于EF）有3条，【解答】解：图过①如 1， O作PQ⊥EF，交AD于P，BC于Q，则PQ=EF；图②如 2，以点A 为圆为连长则心，以AE 半径画弧，交AD于P，接PO并延交BC于Q， PQ=E F；图为圆为连长则心，以AE 半径画弧，交AB于Q，接QO并延交DC于点P， PQ= ③如 3，以B EF．评【点】本题查质质了正方形的性和全等三角形的性与判定，本题虽线然是做一条段与考实际线上是做好两件事：①画段PQ，②能证这线两条段相等，这证为明更 EF相等，明比杂边长题线的段不止一复，因此首先要构建直角三角形全等，找到与EF相等的的位置，本丢条，容易解，要思考周全．　图线动16．如，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在段AB上运（不与A、B重别线给结论：合），将△CAD与△CBD分沿直 CA、CB翻折得到△CAP与△CBQ，出下列 ①CD=CP=CQ；变②∠PCQ的大小不；积③△PCQ面的最小值为；时边④当点D在AB的中点，△PDQ是等三角形，结论其中所有正确的序号是　①②④　．变换综题．【考点】几何合结论【分析】①由折叠直接得到；质义②由折叠的性求出∠ACP+∠BCQ=120°，再用周角的意求出∠PCQ=120°； CD2，判断出边③先作出△PCQ的 PC上的高，用三角函数求出QE= CQ，得到S△PCQ =积时△PCQ面最小，点D的位置，求出最小的CD=CF，即可；边边④先判断出△APD是等三角形，△BDQ是等三角形，再求出∠PDQ=60°，即可．别线【解答】解：①∵将△CAD与△CBD分沿直 CA、CB翻折得到△CAP与△CBQ， ∴CP=CD=CQ， ∴①正确；别线②∵将△CAD与△CBD分沿直 CA、CB翻折得到△CAP与△CBQ， ∴∠ACP=∠ACD，∠BCQ=∠BCD， ∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°， ﹣﹣∴∠PCQ=360° （∠ACP+BCQ+∠ACB）=360° （120°+120°）=120°，变∴∠PCQ的大小不 ∴②正确；；图③如，过长线于E，点Q作QE⊥PC交PC延 ∵∠PCQ=120°， ∴∠QCE=60°，在Rt△QCE中，tan∠QCE= ，∴QE=CQ×tan∠QCE=CQ×tan60°= CQ， ∵CP=CD=CQ ∴S△PCQ= CP×QE= CP×CQ= CD2，时∴CD最短，S△PCQ最小，时即：CD⊥AB ，CD最短，过时点C作CF⊥AB，此 CF就是最短的CD， ∵AC=BC=4，∠ACB=120°， ∴∠ABC=30°， ∴CF= BC=2，为即：CD最短 2， ∴S△PCQ最小 =CD2= ×22=2 ，错误 ∴③ ，别线④∵将△CAD与△CBD分沿直 CA、CB翻折得到△CAP与△CBQ， ∴AD=AP，∠DAC=∠PAC， ∵∠DAC=30°， ∴∠APD=60°，边∴△APD是等三角形， ∴PD=AD，∠ADP=60°，边同理：△BDQ是等三角形， ∴DQ=BD，∠BDQ=60°， ∴∠PDQ=60°， ∵当点D在AB的中点， ∴AD=BD， ∴PD=DQ，边∴△DPQ是等三角形． ∴④正确，为故答案：①②④．评题【点】此是几何变换综题查质质边，主要考了折叠的性，等腰三角形的性，等三角合锐值积题键形的判定，角三角函数，极的确定，三角形的面公式，解本的关是判断出∠PC 值Q=120°是个定；（其实这题还值题难的点是确定出△ 个目中有∠PDQ=60°也是定），解本积时PCQ面最小，点D的位置．　题三、解答（共9小题满，分86分） 0计﹣﹣17．算：（2π） +| 6| ．．实【考点】数的运算；零指数幂计【分析】首先算零次幂绝对值计、开立方，然后算有理数的加减即可．、﹣【解答】解：原式=1+6 2=5．评题【点】此主要考查实键数的运算，关是掌握零指数、开方、等考点的运算幂绝对值了．　18．解分式方程： =．【考点】解分式方程．【分析】先去分母，再解一元一次方程即可．【解答】解：去分母得，3（1+x）=4x，去括号得，3+3x=4x，项移、合并得，x=3，检验：把x=3代入x（x+1）=3×4=12≠0， ∴x=3是原方程的解．评【点】本题查验了解分式方程，解分式方程一定要根．考　组19．解不等式：．组【考点】解一元一次不等式．别【分析】分求出各不等式的解集，再求出其公共解集即可．【解答】解：由①得，x＜3，由②得，x＞1，组为故不等式的解集：1＜x＜3．评【点】本题查组间考的是解一元一次不等式，熟知“同大取大；同小取小；大小小大中找则题键；大大小小找不到”的原是解答此的关．　务办厅发发总统过方案》，一年去了， 20．国院公在2015年3月16日布了《中国足球展改革为识举边专题调查动样的了了解足球知的普及情况，某校行“足球在身 ”的活，采取随机抽果划分 “非常了解”、“比了解”、“基本了解”、“不太了解”四统计图进问调查调查结，为较方法行卷级个等，并将调查结绘图请图（如），根据中提供的信息，解果制成两幅不完整的问题答下列：调查（1）被的学生共有　300　人．统计图较圆为（2）在扇形中，表示“比了解”的扇形的心角度数108　度；该对识（3）从校随机抽取一名学生，抽中的学生足球知是“基本了解”的概率的是多少？统计图统计图．【考点】概率公式；扇形专题统计；条形【】与概率．统计图调查【分析】（1）根据中的数据可以求得本次统计图中的数据可以求得在扇形的人数；中，表示“比了解”的扇形的心角统计图较圆（2）根据条形度数；统计图该对识中的数据可以求得从校随机抽取一名学生，抽中的学生足球知是“ （3）根据基本了解”的概率．【解答】解：（1）由意可得，调查题被的学生有：60÷20%=300（人），为故答案：300；统计图较圆为（2）在扇形中，表示“比了解”的扇形的心角度数：360°× =108°，为故答案：108；题（3）由意可得，该对识从校随机抽取一名学生，抽中的学生足球知是“基本了解”的概率是： =0.4，该对识即从校随机抽取一名学生，抽中的学生足球知是“基本了解”的概率是0.4．统计图统计图题键题，解的关是明确意，找出所评题查【点】本考概率公式、条形、扇形问题．问题结求　需要的条件，利用数形合的思想解答图21．如，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为线E，求段DE的长．质【考点】相似三角形的判定与性．质【分析】根据相似三角形的判定与性，可得答案．【解答】解：∵DE⊥AB， ∴∠BED=90°，又∠C=90°， ∴∠BED=∠C．又∠B=∠B， ∴△BED∽△BCA， ∴=，∴DE= ==4 评【点】本题查质质了相似三角形的判定与性，利用相似三角形的性得出题是解考=键关　．图线为22．如，PA，PB是⊙O的切，A，B 切点，点C在PB上，OC∥AP，CD⊥AP于D 证（1）求：OC=AD；（2）若∠P=50°，⊙O的半径 4，求四形AOCD的周（精确到0.1）为边长线【考点】切的性质．证边【分析】（1）只要明四形OADC是矩形即可．问题（2）在RT△OBC中，根据sin∠BCO= ，求出OC即可解决．证【解答】（1）明：∵PA切⊙O于点A， ∴OA⊥PA，即∠OAD=90°， ∵OC∥AP， ﹣﹣∴∠COA=180° ∠OAD=180° 90°=90°， ∵CD∥PA， ∴∠CDA=∠OAD=∠COA=90°，边∴四形AOCD是矩形， ∴OC=AD．（2）解：∵PB切⊙O于等B， ∴∠OBP=90°， ∵OC∥AP， ∴∠BCO=∠P=50°，在RT△OBC中，sin∠BCO= ，OB=4， ∴OC= ≈5.22，长为 ∴矩形OADC的周 2（OA+OC）=2×（4+5.22）=18.4．评【点】本题查线质质的性、矩形的判定和性等知识题键的关是灵活应这识些知考切解用问题题，属于中考常考型．解决　图23．已知正比例函数y1=ax（a≠0）与反比例函数y2= （k≠0）的象在第一象限内交于点A （2，1）值（1）求a，k的；标这图图时值（2）在直角坐系中画出两个函数的大致象，并根据象直接回答y1＞y2 x的取围范．问题【考点】反比例函数与一次函数的交点．标线值【分析】（1）将A坐代入双曲解析式中，求出k的，确定出反比例函数解析式，将A 标值代入一次函数解析式中，求出a的，确定出一次函数解析式；坐图图时值围范．（2）画出两函数象，由函数象，即可得到y1＞y2 x的取【解答】解：（1）将A（2，1）代入正比例函数解析式得：1=2a，即a= ，故y1= x；线将A（2，1）代入双曲解析式得：1= ，即k=2，故y2= ；图（2）如所示：图时﹣，2＜x＜0或x＞2．由象可得：当y1＞y2 评【点】此题查问题识，涉及的知有：待定系数法确定考了反比例函数与一次函数的交点结结函数解析式，利用了数形合的思想，数形合是数学中重要的思想方法．　2线24．（12分）（2016•南平）已知，抛物 y=ax （a≠0）经过点A（4，4），线（1）求抛物的解析式；图线为边请（2）如 1，抛物上存在点B，使得△AOB是以AO 直角的直角三角形，直接写出标﹣﹣所有符合条件的点B的坐：　B（ 4，4）或（ 8，16）　．线经过﹣ 轴为线点C（0， 1），且平行与x ，若点D 抛物上任意一点（原点图（3）如 2，直 l线过线证线经过点G O除外），直 DO交l于点E，点E作EF⊥l，交抛物于点F，求：直 DF一定（0，1）．综题．【考点】二次函数合线【分析】（1）利用待定系数法求出抛物解析式，线线联（2）分两种情况，先确定出直 OB或AB，和抛物解析式立确定出点B的解析式；设标标进线标线而得出直 DF解析式，将点G坐代入直 DF （3）先出点D坐，确定出点F坐，满看是否足解析式． 2线【解答】解：（1）∵抛物 y=ax （a≠0）经过点A（4，4）， ∴16a=4， ∴a= ， 2线为∴抛物的解析式 y= x，为边（2）存在点B，使得△AOB是以AO 直角的直角三角形，图理由：如 1，为边∵使得△AOB是以AO 直角的直角三角形顶∴直角点是点O，或点A，顶①当直角点是点O 时过线点O作OB⊥OA，交抛物于点B，，∵点A（4，4），线为∴直 OA解析式 y=x，线为﹣∴直 OB解析式 y= x， ∵∴，（舍）或，﹣∴B（ 4，4），顶为过点A，点A作AB⊥OA， ②当直角点线为由①有，直 OA的解析式 y=x， ∵A（4，4），线为﹣∴直 AB解析式 y= x+8， ∵，（舍）或，﹣∴B（ 8，16），满∴﹣ ﹣ 足条件的点B（ 4，4）或（ 8，16）；为﹣﹣故答案 B（ 4，4）或（ 8，16）；（3）明：点D（m， m2），证设线为∴直 DO解析式 y= x，轴﹣∵l∥x ，C（0， 1）， ﹣则﹣令y= 1， x= ，线∴直 DO与l交于E（ ﹣﹣，1），轴∵EF⊥l，l∥x ，标为﹣ ∴F横坐，线∵点F在抛物上， ﹣∴F（，）设线为DF解析式 y=kx+b，直∴，∴，线为∴直 DF解析式 y= x+1，满线∴点G（0，1）足直 DF解析式，线∴直 DF一定经过点G．评题【点】此是二次函数综题查图标，主要考了待定系数法，函数象的交点坐，直角三合质线题键标线角形的性，判断点是否在直上，解本的关是确定出点B的坐，确定出直 DF的题难点．解析式是解本　的线边线线25．已知在矩形ABCD中，∠ADC的平分 DE与BC 所在的直交于点E，点P是段DE 上一定点（其中EP＜PD）图边绕时针转边90°后，角的两（1）如 1，若点F在CD 上（不与D重合），将∠DPF 点P逆旋别线PD、PF分交射 DA于点H、G．证①求：PG=PF；间样证结论 ②探究：DF、DG、DP之有怎的数量关系，并明你的．图（2）拓展：如 2，若点F在CD的延长线过线上（不与D重合），点P作PG⊥PF，交射 DA 认为间（1）中DE、DG、DP之的数量关系是否仍然成立？若成立，给证出明；于点G，你请若不成立，写出它们满说足的数量关系式，并明理由．所边综题．【考点】四形合证证转【分析】（1）①若 PG=PF，可 △HPG≌△DPF，已知∠DPH=∠HPG，由旋可知∠GPF 为=∠HPD=90°及DE平分∠ADC得△HPD 等腰直角三角形，即∠DHP=∠PDF=45°、PD=PH，证即可得；为②由△HPD 等腰直角三角形，△HPG≌△DPF知HD= DP，HG=DF，根据DG+DF=DG+G H=DH即可得；过线证为（2）点P作PH⊥PD交射 DA于点H，先 △HPD 等腰直角三角形可得PH=PD，HD= 证﹣﹣﹣DP，再 △HPG≌△DPF可得HG=DF，根据DH=DG HG=DG DF可得DG DF=DP ．【解答】解：（1）①∵∠GPF=∠HPD=90°，∠ADC=90°， ∴∠GPH=∠FPD， ∵DE平分∠ADC， ∴∠PDF=∠ADP=45°，为∴△HPD 等腰直角三角形， ∴∠DHP=∠PDF=45°，在△HPG和△DPF中， ∵，∴△HPG≌△DPF（ASA）， ∴PG=PF；结论 ②：DG+DF= DP，为由①知，△HPD 等腰直角三角形，△HPG≌△DPF， ∴HD= DP，HG=DF， ∴HD=HG+DG=DF+DG， ∴DG+DF= DP；应为 ﹣：DG DF=DP，（2）不成立，数量关系式图过线点P作PH⊥PD交射 DA于点H，如，∵PF⊥PG， ∴∠GPF=∠HPD=90°， ∴∠GPH=∠FPD， ∵DE平分∠ADC，且在矩形ABCD中，∠ADC=90°，为∴∠HDP=∠EDC=45°，得到△HPD 等腰直角三角形， ∴∠DHP=∠EDC=45°，且PH=PD，HD= DP， ﹣∴∠GHP=∠FDP=180° 45°=135°，在△HPG和△DPF中， ∵∴△HPG≌△DPF， ∴HG=DF， ﹣﹣∴DH=DG HG=DG DF， ﹣∴DG DF=DP．评题查质质质的【点】本主要考等腰直角三角形的性、全等三角形的判定与性、矩形的性证线间段关系综质转线合运用，灵活运用全等三角形的判定与性将待求段关系移至其他两题是解的关键．