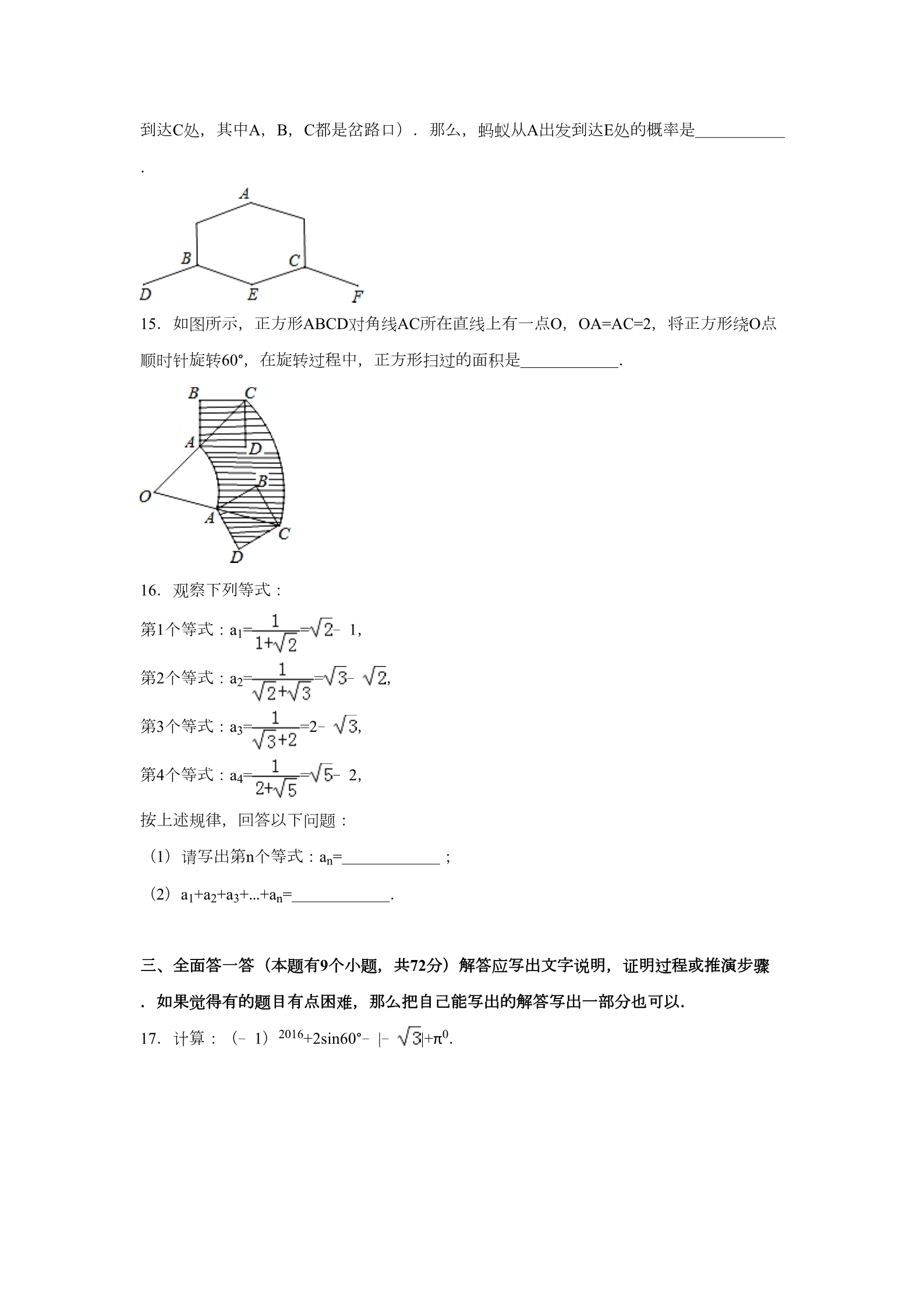
2016年湖北省黄石市中考数学试卷（含解析版）

2016年湖北省黄石市中考数学试卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每个小题给出的四个选项中，只有一个是正确的，请把正确选项所对应的字母在答题卷中相应的格子涂黑．注意可用多种不同的方法来选取正确答案． 1．的倒数是（　　） A． B．2 C．﹣2 D．﹣ 2．下列图形中，既是轴对称图形又是中心对称图形的是（　　） A． B． C． D． 3．地球的平均半径约为6 371 000米，该数字用科学记数法可表示为（　　） A．0.6371×107 B．6.371×106 C．6.371×107 D．6.371×103 4．如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（　　） A．50° B．100° C．120° D．130° 5．下列运算正确的是（　　） A．a3•a2=a6 B．a12÷a3=a4 C．a3+b3=（a+b）3 D．（a3）2=a6 6．黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%，请估计黄石地区1000 斤蚕豆种子中不能发芽的大约有（　　） A．971斤 B．129斤 C．97.1斤 D．29斤 7．某几何体的主视图和左视图如图所示，则该几何体可能是（　　） A．长方体 B．圆锥 C．圆柱 D．球 8．如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON=（　　） A．5 B．7 C．9 D．11 9．以x为自变量的二次函数y=x2﹣2（b﹣2）x+b2﹣1的图象不经过第三象限，则实数b的取值范围是（　　） A．b≥ B．b≥1或b≤﹣1 C．b≥2 D．1≤b≤2 10．如图所示，向一个半径为R、容积为V的球形容器内注水，则能够反映容器内水的体积 y与容器内水深x间的函数关系的图象可能是（　　） A． B． C． D．　二、认真填一填（本题有6个小题，每小题3分，共18分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案． 11．因式分解：x2﹣36=　　　　　　． 12．关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负，则实数m的取值范围是　　　　　　．13．如图所示，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔4海里的A处，该海轮沿南偏东30°方向航行　　　　　　海里后，到达位于灯塔P的正东方向的B处． 14．如图所示，一只蚂蚁从A点出发到D，E，F处寻觅食物．假定蚂蚁在每个岔路口都可能的随机选择一条向左下或右下的路径（比如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A，B，C都是岔路口）．那么，蚂蚁从A出发到达E处的概率是　　　　　　．15．如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是　　　　　　． 16．观察下列等式：第1个等式：a1= 第2个等式：a2= 第3个等式：a3= 第4个等式：a4= =﹣1， ﹣=，=2﹣ ，=﹣2，按上述规律，回答以下问题：（1）请写出第n个等式：an=　　　　　　；（2）a1+a2+a3+…+an=　　　　　　．　三、全面答一答（本题有9个小题，共72分）解答应写出文字说明，证明过程或推演步骤．如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以． 17．计算：（﹣1）2016+2sin60°﹣|﹣ |+π0． 18．先化简，再求值： ÷•，其中a=2016． 19．如图，⊙O的直径为AB，点C在圆周上（异于A，B），AD⊥CD．（1）若BC=3，AB=5，求AC的值；（2）若AC是∠DAB的平分线，求证：直线CD是⊙O的切线． 20．解方程组．21．为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况，现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本．体育成绩分为四个等次：优秀、良好、及格、不及格．体育锻炼时间 4≤x≤6 人数　　　 2≤x＜4 43 15 0≤x＜2 （1）试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数；（2）统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表（如图表所示），请将图表填写完整（记学生课外体育锻炼时间为x小时）；（3）全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”，请估计这些学生中课外体育锻炼时间不少于4小时的学生人数． 22．如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．（1）求AB段山坡的高度EF；（2）求山峰的高度CF．（ 1.414，CF结果精确到米） 23．科技馆是少年儿童节假日游玩的乐园．如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为y= ，1 0：00之后来的游客较少可忽略不计．（1）请写出图中曲线对应的函数解析式；（2）为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到 624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？ 24．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．（1）如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；（3）如图3，若α=45°，点E在BC的延长线上，则等式DE2=BD2+CE2还能成立吗？请说明理由． 25．如图1所示，已知：点A（﹣2，﹣1）在双曲线C：y= 上，直线l1：y=﹣x+2，直线l2 与l1关于原点成中心对称，F1（2，2），F2（﹣2，﹣2）两点间的连线与曲线C在第一象限内的交点为B，P是曲线C上第一象限内异于B的一动点，过P作x轴平行线分别交l1，l2于M ，N两点．（1）求双曲线C及直线l2的解析式；（2）求证：PF2﹣PF1=MN=4；（3）如图2所示，△PF1F2的内切圆与F1F2，PF1，PF2三边分别相切于点Q，R，S，求证：点Q与点B重合．（参考公式：在平面坐标系中，若有点A（x1，y1），B（x2，y2），则A 、B两点间的距离公式为AB= ．）　2016年湖北省黄石市中考数学试卷参考答案与试题解析一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每个小题给出的四个选项中，只有一个是正确的，请把正确选项所对应的字母在答题卷中相应的格子涂黑．注意可用多种不同的方法来选取正确答案． 1．的倒数是（　　） A． B．2 C．﹣2 D．﹣ 【分析】直接利用倒数的定义分析求出答案．【解答】解：∵2× =1， ∴的倒数是：2．故选：B．【点评】此题主要考查了倒数的定义，正确把握定义是解题关键．　2．下列图形中，既是轴对称图形又是中心对称图形的是（　　） A． B． C． D．【分析】依据轴对称图形的定义和中心对称图形的定义回答即可．【解答】解：A、是轴对称图形，但不是中心对称图形，故A错误； B、是轴对称图形，也是中心对称图形，故B正确； C、是中心对称图形，但不是轴对称图形，故C错误； D、是轴对称图形，但不是中心对称图形，故D错误．故选：B．【点评】本题主要考查的是轴对称图形和中心对称图形，掌握轴对称图形和中心对称图形的特点是解题的关键．　3．地球的平均半径约为6 371 000米，该数字用科学记数法可表示为（　　） A．0.6371×107B．6.371×106C．6.371×107D．6.371×103 【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：6 371 000=6.371×106，故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤| a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　4．如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（　　） A．50° B．100° C．120° D．130° 【分析】根据线段垂直平分线的性质得到DA=DC，根据等腰三角形的性质得到∠DCA=∠A ，根据三角形的外角的性质计算即可．【解答】解：∵DE是线段AC的垂直平分线， ∴DA=DC， ∴∠DCA=∠A=50°， ∴∠BDC=∠DCA+∠A=100°，故选：B．【点评】本题考查的是线段垂直平分线的性质和三角形的外角的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．　5．下列运算正确的是（　　） A．a3•a2=a6B．a12÷a3=a4C．a3+b3=（a+b）3D．（a3）2=a6 【分析】根据同底数幂的乘除法、合并同类项以及幂的乘方与积的乘方计算法则进行解答．【解答】解：A、原式=a3+2=a5，故本选项错误； B、原式=a12﹣3=a9，故本选项错误； C、右边=a3+3a2b+3ab2+b3≠左边，故本选项错误； D、原式=a3×2=a6，故本选项正确．故选：D．【点评】本题考查了同底数幂的乘除法、合并同类项以及幂的乘方与积的乘方，熟记计算法则即可解答该题．　6．黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%，请估计黄石地区1000 斤蚕豆种子中不能发芽的大约有（　　） A．971斤 B．129斤 C．97.1斤 D．29斤【分析】根据蚕豆种子的发芽率为97.1%，可以估计黄石地区1000斤蚕豆种子中不能发芽的大约有多少，本题得以解决．【解答】解：由题意可得，黄石地区1000斤蚕豆种子中不能发芽的大约有：1000×（1﹣97.1%）=1000×0.029=29斤，故选D．【点评】本题考查用样本估计总体，解题的关键是明确题意，注意求得是不能发芽的种子数．　7．某几何体的主视图和左视图如图所示，则该几何体可能是（　　） A．长方体 B．圆锥 C．圆柱 D．球【分析】主视图、左视图是分别从物体正面、左面看，所得到的图形，根据该几何体的主视图和左视图都是长方形，可得该几何体可能是圆柱体．【解答】解：∵如图所示几何体的主视图和左视图， ∴该几何体可能是圆柱体．故选C．【点评】本题考查由三视图确定几何体的形状，主要考查学生空间想象能力，掌握常见几何体的三视图是解题的关键．　8．如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON=（　　） A．5 B．7 C．9 D．11 【分析】根据⊙O的半径为13，弦AB的长度是24，ON⊥AB，可以求得AN的长，从而可以求得ON的长．【解答】解：由题意可得， OA=13，∠ONA=90°，AB=24， ∴AN=12， ∴ON= ，故选A．【点评】本题考查垂径定理，解题的关键是明确垂径定理的内容，利用垂径定理解答问题．　9．以x为自变量的二次函数y=x2﹣2（b﹣2）x+b2﹣1的图象不经过第三象限，则实数b的取值范围是（　　） A．b≥ B．b≥1或b≤﹣1 C．b≥2 D．1≤b≤2 【分析】由于二次函数y=x2﹣2（b﹣2）x+b2﹣1的图象不经过第三象限，所以抛物线在x轴的上方或在x轴的下方经过一、二、四象限，根据二次项系数知道抛物线开口方向向上，由此可以确定抛物线与x轴有无交点，抛物线与y轴的交点的位置，由此即可得出关于b的不等式组，解不等式组即可求解．【解答】解：∵二次函数y=x2﹣2（b﹣2）x+b2﹣1的图象不经过第三象限， ∴抛物线在x轴的上方或在x轴的下方经过一、二、四象限，当抛物线在 x轴的上方时， ∵二次项系数a=1， ∴抛物线开口方向向上， ∴b2﹣1≥0，△=[2（b﹣2）]2﹣4（b2﹣1）≤0，解得b≥ ；当抛物线在x轴的下方经过一、二、四象限时，设抛物线与x轴的交点的横坐标分别为x1，x2， ∴x1+x2=2（b﹣2）≥0，b2﹣1≥0， ∴△=[2（b﹣2）]2﹣4（b2﹣1）＞0，① b﹣2＞0，② b2﹣1＞0， ③ 由①得b＜，由②得b＞2， ∴此种情况不存在， ∴b≥ ，故选A．【点评】此题主要考查了二次函数的图象和性质，解题的关键是会根据图象的位置得到关于b的不等式组解决问题．　10．如图所示，向一个半径为R、容积为V的球形容器内注水，则能够反映容器内水的体积 y与容器内水深x间的函数关系的图象可能是（　　） A． B． C． D．【分析】水深h越大，水的体积v就越大，故容器内水的体积y与容器内水深x间的函数是增函数，根据球的特征进行判断分析即可．【解答】解：根据球形容器形状可知，函数y的变化趋势呈现出，当0＜x＜R时，y增量越来越大，当R＜x＜2R时，y增量越来越小，曲线上的点的切线斜率先是逐渐变大，后又逐渐变小，故y关于x的函数图象是先凹后凸．故选（A）【点评】本题主要考查了函数图象的变化特征，解题的关键是利用数形结合的数学思想方法．解得此类试题时注意，如果把自变量与函数的每一对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形就是这个函数的图象．　二、认真填一填（本题有6个小题，每小题3分，共18分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案． 11．因式分解：x2﹣36=　（x+6）（x﹣6）　．【分析】直接用平方差公式分解．平方差公式：a2﹣b2=（a+b）（a﹣b）．【解答】解：x2﹣36=（x+6）（x﹣6）．【点评】本题主要考查利用平方差公式分解因式，熟记公式结构是解题的关键．　12．关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负，则实数m的取值范围是　 m＞．【分析】设x1、x2为方程x2+2x﹣2m+1=0的两个实数根．由方程有实数根以及两根之积为负可得出关于m的一元一次不等式组，解不等式组即可得出结论．【解答】解：设x1、x2为方程x2+2x﹣2m+1=0的两个实数根，由已知得：，即解得：m＞．故答案为：m＞．【点评】本题考查了根与系数的关系、根的判别式以及解一元一次不等式，解题的关键是得出关于m的一元一次不等式组．本题属于基础题，难度不大，解决该题型题目时，根据根的情况结合根的判别式以及根与系数的关系得出关于m的一元一次不等式组是关键．　13．如图所示，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔4海里的A处，该海轮沿南偏东30°方向航行　4　海里后，到达位于灯塔P的正东方向的B处．【分析】根据等腰三角形的性质，可得答案．【解答】解：一艘海轮位于灯塔P的北偏东30°方向，距离灯塔4海里的A处，该海轮沿南偏东30°方向航行 4海里后，到达位于灯塔P的正东方向的B处故答案为：4．【点评】本题考查了等腰三角形的性质，利用了等腰三角形的腰相等是解题关键．　14．如图所示，一只蚂蚁从A点出发到D，E，F处寻觅食物．假定蚂蚁在每个岔路口都可能的随机选择一条向左下或右下的路径（比如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A，B，C都是岔路口）．那么，蚂蚁从A出发到达E处的概率是　．【分析】首先根据题意可得共有4种等可能的结果，蚂蚁从A出发到达E处的2种情况，然后直接利用概率公式求解即可求得答案．【解答】解：画树状图得： ∵共有4种等可能的结果，蚂蚁从A出发到达E处的2种情况， ∴蚂蚁从A出发到达E处的概率是：故答案为： = ．．【点评】此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．　15．如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是　2π+2　．【分析】如图，用大扇形的面积减去小扇形的面积再加上正方形ABCD的面积．【解答】解：∵OA=AC=2， ∴AB=BC=CD=AD= ，OC=4， S阴影 =+=2π+2，故答案为：2π+2．【点评】此题考查了扇形的面积公式和旋转的性质以及勾股定理，能够把不规则图形的面积转换为规则图形的面积是解答此题的关键．　16．观察下列等式：第1个等式：a1= 第2个等式：a2= 第3个等式：a3= 第4个等式：a4= =﹣1， ﹣=，=2﹣ ，=﹣2，按上述规律，回答以下问题：（1）请写出第n个等式：an=　 =﹣；　；（2）a1+a2+a3+…+an=　【分析】（1）根据题意可知，a1= ，a4= （2）将每一个等式化简即可求得答案． ﹣1　． =﹣1，a2= =﹣，a3= =2﹣ =﹣2，…由此得出第n个等式：an= =﹣；【解答】解：（1）∵第1个等式：a1= =﹣1，第2个等式：a2= 第3个等式：a3= 第4个等式：a4= ∴第n个等式：an= （2）a1+a2+a3+…+an ==2﹣ =﹣，，﹣2， =﹣；=（ ﹣1）+（ ﹣1．故答案为 ﹣）+（2﹣ ）+（ ﹣2）+…+（ ﹣）==﹣；﹣1．【点评】此题考查数字的变化规律以及分母有理化，要求学生首先分析题意，找到规律，并进行推导得出答案．　三、全面答一答（本题有9个小题，共72分）解答应写出文字说明，证明过程或推演步骤．如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以． 17．计算：（﹣1）2016+2sin60°﹣|﹣ |+π0．【分析】根据实数的运算顺序，首先计算乘方和乘法，然后从左向右依次计算，求出算式（﹣1）2016+2sin60°﹣|﹣ |+π0的值是多少即可．【解答】解：（﹣1）2016+2sin60°﹣|﹣ |+π0 =1+2× ﹣+1 =1+ =2 ﹣+1 【点评】（1）此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行．另外，有理数的运算律在实数范围内仍然适用．（2）此题还考查了零指数幂的运算，要熟练掌握，解答此题的关键是要明确：①a0=1（a ≠0）；②00≠1．（3）此题还考查了特殊角的三角函数值，要牢记30°、45°、60°角的各种三角函数值．　18．先化简，再求值： ÷•，其中a=2016．【分析】先算除法，再算乘法，把分式化为最简形式，最后把a=2016代入进行计算即可．【解答】解：原式= =（a﹣1）• ••=a+1，当a=2016时，原式=2017．【点评】本题考查的是分式的化简求值，在解答此类问题时要注意把分式化为最简形式，再代入求值．　19．如图，⊙O的直径为AB，点C在圆周上（异于A，B），AD⊥CD．（1）若BC=3，AB=5，求AC的值；（2）若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．【分析】（1）首先根据直径所对的圆周角为直角得到直角三角形，然后利用勾股定理求得 AC的长即可；（2）连接OC，证OC⊥CD即可；利用角平分线的性质和等边对等角，可证得∠OCA=∠CAD ，即可得到OC∥AD，由于AD⊥CD，那么OC⊥CD，由此得证．【解答】（1）解：∵AB是⊙O直径，C在⊙O上， ∴∠ACB=90°，又∵BC=3，AB=5， ∴由勾股定理得AC=4；（2）证明：∵AC是∠DAB的角平分线， ∴∠DAC=∠BAC，又∵AD⊥DC， ∴∠ADC=∠ACB=90°， ∴△ADC∽△ACB， ∴∠DCA=∠CBA，又∵OA=OC， ∴∠OAC=∠OCA， ∵∠OAC+∠OBC=90°， ∴∠OCA+∠ACD=∠OCD=90°， ∴DC是⊙O的切线．【点评】此题主要考查的是切线的判定方法．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．　20．解方程组．【分析】首先联立方程组消去x求出y的值，然后再把y的值代入x﹣y=2中求出x的值即可．【解答】解：将两式联立消去x得： 9（y+2）2﹣4y2=36，即5y2+36y=0，解得：y=0或﹣ 当y=0时，x=2，，y=﹣ 时，x=﹣ ；原方程组的解为或．【点评】本题主要考查了高次方程的知识，解答本题的关键是进行降次解方程，此题难度不大．　21．为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况，现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本．体育成绩分为四个等次：优秀、良好、及格、不及格．体育锻炼时间 4≤x≤6 人数　62　 43 2≤x＜4 0≤x＜2 15 （1）试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数；（2）统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表（如图表所示），请将图表填写完整（记学生课外体育锻炼时间为x小时）；（3）全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”，请估计这些学生中课外体育锻炼时间不少于4小时的学生人数．【分析】（1）直接利用扇形统计图得出体育成绩“良好”所占百分比，进而求出所对扇形圆心角的度数；（2）首先求出体育成绩“优秀”和“良好”的学生数，再利用表格中数据求出答案；（3）直接利用“优秀”和“良好”学生所占比例得出学生中课外体育锻炼时间不少于4小时的学生人数．【解答】解：（1）由题意可得：样本扇形图中体育成绩“良好”所对扇形圆心角的度数为：（1﹣15%﹣14%﹣26%）×360°=1 62°；（2）∵体育成绩“优秀”和“良好”的学生有：200×（1﹣14%﹣26%）=120（人）， ∴4≤x≤6范围内的人数为：120﹣43﹣15=62（人）；故答案为：62；（3）由题意可得： ×14400=7440（人），答：估计课外体育锻炼时间不少于4小时的学生人数为7440人．【点评】此题主要考查了扇形统计图以及利用样本估计总体，正确利用扇形统计图和表格中数据得出正确信息是解题关键．　22．如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．（1）求AB段山坡的高度EF；（2）求山峰的高度CF．（ 1.414，CF结果精确到米）【分析】（1）作BH⊥AF于H，如图，在Rt△ABF中根据正弦的定义可计算出BH的长，从而得到EF的长；（2）先在Rt△CBE中利用∠CBE的正弦计算出CE，然后计算CE和EF的和即可．【解答】解：（1）作BH⊥AF于H，如图，在Rt△ABF中，∵sin∠BAH= ，∴BH=800•sin30°=400， ∴EF=BH=400m；（2）在Rt△CBE中，∵sin∠CBE= ∴CE=200•sin45°=100 ≈141.4，，∴CF=CE+EF=141.4+400≈541（m）．答：AB段山坡高度为400米，山CF的高度约为541米．【点评】本题考查了解直角三角形的应用﹣坡度与坡角问题：坡度是坡面的铅直高度h和水平宽度l的比，又叫做坡比，它是一个比值，反映了斜坡的陡峭程度，一般用i表示，常写成i=1：m的形式．把坡面与水平面的夹角α叫做坡角，坡度i与坡角α之间的关系为：i═tanα ．　23．科技馆是少年儿童节假日游玩的乐园．如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为y= ，1 0：00之后来的游客较少可忽略不计．（1）请写出图中曲线对应的函数解析式；（2）为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到 624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？【分析】（1）构建待定系数法即可解决问题．（2）先求出馆内人数等于684人时的时间，再求出直到馆内人数减少到624人时的时间，即可解决问题．【解答】解（1）由图象可知，300=a×302，解得a= ，n=700，b×（30﹣90）2+700=300，解得b=﹣ ，∴y= ，（2）由题意﹣ （x﹣90）2+700=684，解得x=78， ∴=15， ∴15+30+（90﹣78）=57分钟所以，馆外游客最多等待57分钟．【点评】本题考查二次函数的应用、一元二次方程等知识，解题的关键是熟练掌握待定系数法，学会用方程的思想思考问题，属于中考常考题型．　24．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．（1）如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；（3）如图3，若α=45°，点E在BC的延长线上，则等式DE2=BD2+CE2还能成立吗？请说明理由．【分析】（1）根据轴对称的性质可得∠EAF=∠DAE，AD=AF，再求出∠BAC=∠DAF，然后根据两边对应成比例，夹角相等两三角形相似证明；（2）根据轴对称的性质可得EF=DE，AF=AD，再求出∠BAD=∠CAF，然后利用“边角边” 证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠ECF=90°，最后利用勾股定理证明即可；（3）作点D关于AE的对称点F，连接EF、CF，根据轴对称的性质可得EF=DE，AF=AD，再根据同角的余角相等求出∠BAD=∠CAF，然后利用“边角边”证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠ ECF=90°，最后利用勾股定理证明即可．【解答】证明：（1）∵点D关于直线AE的对称点为F， ∴∠EAF=∠DAE，AD=AF，又∵∠BAC=2∠DAE， ∴∠BAC=∠DAF， ∵AB=AC， ∴=，∴△ADF∽△ABC；（2）∵点D关于直线AE的对称点为F， ∴EF=DE，AF=AD， ∵α=45°， ∴∠BAD=90°﹣∠CAD， ∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD， ∴∠BAD=∠CAF，在△ABD和△ACF中，，∴△ABD≌△ACF（SAS）， ∴CF=BD，∠ACF=∠B， ∵AB=AC，∠BAC=2α，α=45°， ∴△ABC是等腰直角三角形， ∴∠B=∠ACB=45°， ∴∠ECF=∠ACB+∠ACF=45°+45°=90°，在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，所以，DE2=BD2+CE2；（3）DE2=BD2+CE2还能成立．理由如下：作点D关于AE的对称点F，连接EF、CF，由轴对称的性质得，EF=DE，AF=AD， ∵α=45°， ∴∠BAD=90°﹣∠CAD， ∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD， ∴∠BAD=∠CAF，在△ABD和△ACF中，，∴△ABD≌△ACF（SAS）， ∴CF=BD，∠ACF=∠B， ∵AB=AC，∠BAC=2α，α=45°， ∴△ABC是等腰直角三角形， ∴∠B=∠ACB=45°， ∴∠ECF=∠ACB+∠ACF=45°+45°=90°，在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，所以，DE2=BD2+CE2．【点评】本题是相似形综合题，主要利用了轴对称的性质，相似三角形的判定，同角的余角相等的性质，全等三角形的判定与性质，勾股定理，此类题目，小题间的思路相同是解题的关键．　25．如图1所示，已知：点A（﹣2，﹣1）在双曲线C：y= 上，直线l1：y=﹣x+2，直线l2 与l1关于原点成中心对称，F1（2，2），F2（﹣2，﹣2）两点间的连线与曲线C在第一象限内的交点为B，P是曲线C上第一象限内异于B的一动点，过P作x轴平行线分别交l1，l2于M ，N两点．（1）求双曲线C及直线l2的解析式；（2）求证：PF2﹣PF1=MN=4；（3）如图2所示，△PF1F2的内切圆与F1F2，PF1，PF2三边分别相切于点Q，R，S，求证：点Q与点B重合．（参考公式：在平面坐标系中，若有点A（x1，y1），B（x2，y2），则A 、B两点间的距离公式为AB= ．）【分析】（1）利用点A的坐标求出a的值，根据原点对称的性质找出直线l2上两点的坐标，求出解析式；（2）设P（x，），利用两点距离公式分别求出PF1、PF2、PM、PN的长，相减得出结论；（3）利用切线长定理得出，并由（2）的结论PF2﹣PF1=4得出PF2﹣PF1=QF2 ﹣QF1=4，再由两点间距离公式求出F1F2的长，计算出OQ和OB的长，得出点Q与点B重合．【解答】解：（1）解：把A（﹣2，﹣1）代入y= 中得： a=（﹣2）×（﹣1）=2， ∴双曲线C：y= ，∵直线l1与x轴、y轴的交点分别是（2，0）、（0，2），它们关于原点的对称点分别是（﹣ 2，0）、（0，﹣2）， ∴l2：y=﹣x﹣2 （2）设P（x，）， 2由F1（2，2）得：PF1 =（x﹣2）2+（ ﹣2）2=x2﹣4x+ ﹣ +8， 2∴PF1 =（x+ ﹣2）2， ∵x+ ﹣2= =＞0， ∴PF1=x+ ﹣2， ∵PM∥x轴 ∴PM=PE+ME=PE+EF=x+ ﹣2， ∴PM=PF1， 2同理，PF2 =（x+2）2+（ +2）2=（x+ +2）2， ∴PF2=x+ +2，PN=x+ +2 因此PF2=PN， ∴PF2﹣PF1=PN﹣PM=MN=4，（3）△PF1F2的内切圆与F1F2，PF1，PF2三边分别相切于点Q，R，S， ∴⇒PF2﹣PF1=QF2﹣QF1=4 又∵QF2+QF1=F1F2=4 ，QF1=2 ﹣2， ∴QO=2， ∵B（，）， ∴OB=2=OQ，所以，点Q与点B重合．【点评】此题主要考查了圆的综合应用以及反比例函数的性质等知识，将代数与几何融合在一起，注意函数中线段的长可以利用本题给出的两点距离公式解出，也可以利用勾股定理解出；解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．