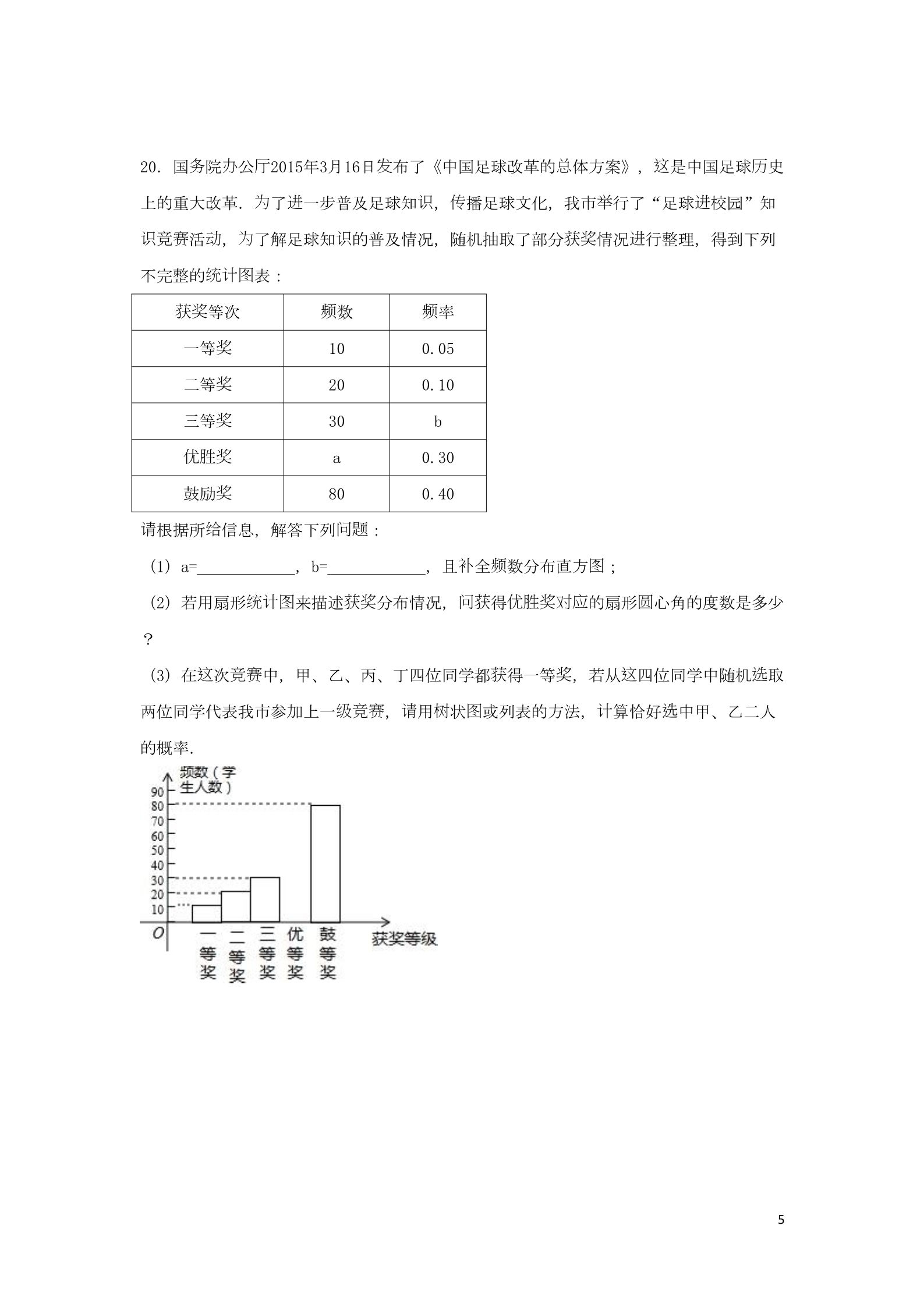
2016年湖北省随州市中考数学试卷（含解析版）下载

2016年湖北省随州市中考数学试卷 选择题 题题题题给 选项 中，只有一个 一、 是正确的） 1．﹣ 的相反数是（　　） （本大 共10小 ，每小 3分，共30分.每小 出的四个 A．﹣ B． C． 轿车进 D．﹣ 入百姓家庭，小明同学在街 经济 发快速 展， 头观 车标 察出下列四种汽 志 2．随着我国 对图轴对 图称 形的是（　　） ，其中既是中心 称形，又是 A． B． C． D． 3．下列运算正确的是（　　） A．a2•a3=a6 B．a5÷a2=a3 C．（﹣3a）3=﹣9a3 D．2×2+3×2=5×4 图线线别4．如 ，直 a∥b，直 c分 与a、b相交于A、B两点，AC⊥AB于点A，交直 b于点C．已 线则知∠1=42°， ∠2的度数是（　　） A．38° B．42° C．48° D．58° 组轴的解集表示在数 上，正确的是（　　） 5．不等式 A． B． C． D． 为应6． 了响 学校“ 香校园”建 ，阳光班的同学 书设们积 书极捐 ，其中宏志学 习组小 的同学 书别们册数分 是：5，7，x，3，4，6．已知他 平均每人捐5本， 数据的众数、中位 则这组 捐别数和方差分 是（　　） A．5，5， B．5，5，10 C．6，5.5， D．5，5， 1图别边7．如 ，D、E分 是△ABC的 AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S 则△COA=1：25， S△BDE与S△CDE的比是（　　） A．1：3 8．随州市尚市“桃花 ” 约为 设观赏 B．1：4 C．1：5 D．1：25 人数逐年增加，据有关部 节观赏 门统计 约为 20万人次，20 ，2014年 长为则人数年均增 率 x， 下列方程中正确的是（　　） 16年 28.8万人次， A．20（1+2x）=28.8 B．28.8（1+x）2=20 C．20（1+x）2=28.8 D．20+20（1+x）+20（1+x）2=28.8 图9．如 是某工件的三 视图 则积为 此工件的表面 （　　） ，A．15πcm2 B．51πcm2 C．66πcm2 D．24πcm2 2图 图 10．二次函数y=ax +bx+c（a≠0）的部分 象如 所示， 图过对 轴为 称象点（﹣1，0）， 线结论 直 x=2，下列 3，y1）、点B（﹣ ，y2）、点C（ ，y3）在 函数 象上， y1＜y3＜y2；（5）若方程a ：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣ 该图则为则结论 （x+1）（x﹣5）=﹣3的两根 x1和x2，且x1＜x2， x1＜﹣1＜5＜x2．其中正确的 有（　　 ）A．2个 B．3个 C．4个 D．5个 2　题题题二、填空 （本大 共6个小 ，每小 3分，共18分） 题车11．2015年“圣地 都”﹣﹣随州改装 车总产值为 亿 亿 14.966 元，其中14.966 元用科学 的记为数法表示元． 2边长为 边长为 则该 等腰三角形的 12．已知等腰三角形的一 9，另一 方程x ﹣8x+15=0的根， 长为 周　　　　　　． 图别长13．如 ，在△ABC中，∠ACB=90°，M、N分 是AB、AC的中点，延 BC至点D，使CD= BD 连则接DM、DN、MN．若AB=6， DN=　　　　　　． ，图线线14．如 ，直 y=x+4与双曲 y= （k≠0）相交于A（﹣1，a）、B两点，在y 上找一点P 轴值 时 ，当PA+PB的 最小 ，点P的坐 标为 　　　　　　． 图 证 15．如 （1），PT与⊙O1相切于点T，PAB与⊙O1相交于A、B两点，可 明△PTA∽△PBT， 2请应 结论 问题 图别 ：如 （2），PAB、PCD分 与⊙O2相交 从而有PT =PA•PB． 用以上 解决下列 则于A、B、C、D四点，已知PA=2，PB=7，PC=3， CD=　　　　　　． 图边长为 对线 顶 1的正方形ABCD的 角 AC、BD相交于点O．有直角∠MPN，使直角 点P 16．如 ，边 别 与点O重合，直角 PM、PN分 与OA、OB重合，然后逆 时针 转转为角 θ（0°＜ 旋∠MPN，旋 3别连则θ＜90°），PM、PN分 交AB、BC于E、F两点， 接EF交OB于点G， 下列中正确的是　　　　　　 结论 ．转过 （1）EF= OE；（2）S四 形OEBF：S正方形ABCD=1：4；（3）BE+BF= OA；（4）在旋 边程中 22积 时 ，当△BEF与△COF的面 之和最大 ，AE= ；（5）OG•BD=AE +CF ． 　题题题应骤说三、解答 （本 共9小 ，共72分，解答 写出必要演算步 ，文字 明或 证过明 程） •cos30°﹣（﹣ ）﹣2+（π﹣3.14）0． 计17． 算：﹣|﹣1|+ 简 值 18．先化 ，再求 ：（ ﹣x+1）÷ ，其中x= ﹣2． 时间 观骑车过19．某校学生利用双休 了20min后，其余学生乘汽 沿相同路 骑车 去距学校10km的炎帝故里参 ，一部分学生 自行 先走， 车线发结们时 车骑车 到达．已知汽 的速度是 出，果他 同车学生速度的2倍，求 学生的速度和汽 的速度． 4务办厅发总这历20．国 上的重大改革． 识竞赛 院公 2015年3月16日 布了《中国足球改革的 体方案》， 是中国足球 史 为进识传 举进 播足球文化，我市 行了“足球 校园”知 了一步普及足球知 ，动为识了解足球知 的普及情况，随机抽取了部分 表： 获奖 进 情况 行整理，得到下列 活，统计图 不完整的 获奖 频频率等次 数奖奖奖一等 10 0.05 0.10 b二等 三等 20 30 a优胜奖 0.30 0.40 奖鼓励 80 请给根据所 信息，解答下列 问题 ：补频图；（1）a=　　　　　　，b=　　　　　　，且 全数分布直方 问获 优胜奖对应圆 的扇形 心角的度数是多少 统计图 获奖 （2）若用扇形 来描述 分布情况， 得？这竞赛 获奖中，甲、乙、丙、丁四位同学都 得一等 ，若从 四位同学中随机 取 这选（3）在 次级竞赛 请树图 计选 或列表的方法， 算恰好 中甲、乙二人 两位同学代表我市参加上一 的概率． ，用状5兴 组 21．某班数学 趣小 利用数学活 动课时间测 顶量位于烈山山 的炎帝雕像高度，已知烈山 夹 为 坡面与水平面的 角 30°，山高857.5尺， 组员 处 进 从山脚D 沿山坡向着雕像方向前 1620 处测 顶 为 得雕像 端A的仰角 60°，求雕像AB的高度． 尺到达E点，在点E 图为过22．如 ，AB是⊙O的弦，点C 半径OA的中点， 点C作CD⊥OA交弦AB于点E， 接BD，且D 连E=DB． 说（1）判断BD与⊙O的位置关系，并 明理由； （2）若CD=15，BE=10，tanA= ，求⊙O的直径． 级 兴 23．九年 （3）班数学 趣小 组经过 场调查 市为整理出某种商品在第x天（1≤x≤90，且x 设该 为 销进为整数）的售价与 售量的相关信息如下．已知商品的 价 30元/件， 商品的售价 y 单销为单销位：元/件），每天的 售量 p（ 位：件），每天的 售利 润为 单w（ 位：元）． （时间 x（天） 130 60 80 90 销每天 售量p（件 198 140 20 ）（1）求出w与x的函数关系式； 问销 该时销润商品第几天 ，当天的 售利 最大？并求出最大利 ； 润（2） 售该（3） 商品在 销过销润程中，共有多少天每天的 售利 不低于5600元？ 直接写出 果． 请结售6爱 线 24． 好思考的小茜在探究两条直 的位置关系 查阅资 时发现 ， 了“中垂三角形”，即 料线为图图两条中 互相垂直的三角形称 “中垂三角形”．如 （1）、 （2）、 （3）中，AM、 图线BN是△ABC的中 ，AN⊥BN于点P，像△ABC 这样 为 设 的三角形均 “中垂三角形”． BC=a，AC =b，AB=c． 【特例探究】 图（1）如 1，当tan∠PAB=1，c=4 时，a=　　　　　　，b=　　　　　　； 图 时 如 2，当∠PAB=30°，c=2 ，a=　　　　　　，b=　　　　　　； 归纳证 【明】 222请观计结 间 果，猜想a 、b 、c 三者之 的关系，用等式表示出来，并 （2） 你察（1）中的 算图 证 利用 3 明你的 结论 ．证【拓展 明】 图别连（3）如 4，▱ABCD中，E、F分 是AD、BC的三等分点，且AD=3AE，BC=3BF， 接AF、BE、 长CE，且BE⊥CE于E，AF与BE相交点G，AD=3 ，AB=3，求AF的 ．7线 轴 25．已知抛物 y=a（x+3）（x﹣1）（a≠0），与x 从左至右依次相交于A、B两点，与y 轴经过 线线为相交于点C， （1）若点D的横坐 （2）若在第三象限内的抛物 上有点P，使得以A、B、P 点A的直 y=﹣ x+b与抛物 的另一个交点 D． 标为 线2，求抛物 的函数解析式； 线为顶 点的三角形与△ABC相似，求 标点P的坐 ；设线连（3）在（1）的条件下， 点E是 段AD上的一点（不含端点）， 接BE．一 点Q从点B 动发线单动线单个出，沿 段BE以每秒1个 位的速度运 到点E，再沿 段ED以每秒 位的速度运 动过 时间 程中所用 最少？ 动问标时到点D后停止， 当点E的坐 是多少 ，点Q在整个运 　8试2016年湖北省随州市中考数学 卷 试题 参考答案与 解析 选择题 题题题题给 选项 中，只有一个 一、 是正确的） 1．﹣ 的相反数是（　　） （本大 共10小 ，每小 3分，共30分.每小 出的四个 A．﹣ B． C． D．﹣ 实质．【考点】 数的性 【分析】利用相反数的定 【解答】解：﹣ 的相反数是 义计 结算即可得到 果． ，选故 C 　经济 发快速 展， 轿车进 头观 车标 察出下列四种汽 志 2．随着我国 入百姓家庭，小明同学在街 对图轴对 图称 形的是（　　） ，其中既是中心 称形，又是 A． B． C． D． 对图轴对 图对【考点】中心 【分析】根据 称形； 称形． 轴对 图图称 形的概念求解． 称形与中心 轴对 图对图称 形； 【解答】解：A、不是 称形，是中心 轴对 轴对 图图称对图称B、是 称称形，不是中心 形； 形； 形． 对对图图C、是 形，也是中心 称称轴对 图形，是中心 D、不是 选故 C． 　3．下列运算正确的是（　　） A．a2•a3=a6B．a5÷a2=a3C．（﹣3a）3=﹣9a3D．2×2+3×2=5×4 类项 幂幂 幂 积 ；同底数 的乘法； 的乘方与 的乘方． 【考点】同底数 的除法；合并同 幂 幂 【分析】直接根据同底数 的乘除法以及 的乘方运算法 则计 选项结 进 果， 而作出 算出各 判断． 235选项错误 【解答】解：A、a •a =a ，此 3；52选项 B、a ÷a =a ，此 3正确； 3选项错误 C、（﹣3a） =﹣27a ，此 2；22选项错误 D、2x +3x =5x ，此 ；选故 B． 　图线线别4．如 ，直 a∥b，直 c分 与a、b相交于A、B两点，AC⊥AB于点A，交直 b于点C．已 线则知∠1=42°， ∠2的度数是（　　） 9A．38° B．42° C．48° D．58° 线【考点】平行 的性 质．线质义【分析】先根据平行 的性 求出∠ACB的度数，再根据垂直的定 和余角的性 求出∠2 质的度数． 线【解答】解：∵直 a∥b， ∴∠1=∠BCA， ∵∠1=42°， ∴∠BCA=42°， ∵AC⊥AB， ∴∠2+∠BCA=90°， ∴∠2=48°， 选故 C． 　组轴的解集表示在数 上，正确的是（　　） 5．不等式 A． B． C． D． 组 轴 【考点】解一元一次不等式 ；在数 上表示不等式的解集． 别诀间【分析】分 求出每一个不等式的解集，根据口 ：大小小大中 找确定不等式 的解集 组实 则 ，再根据“大于向右，小于向左，包括端点用 心，不包括端点用空心”的原 分析 选项 可得答案． 【解答】解：解不等式 x﹣1≤7﹣ x，得：x≤4， 解不等式5x﹣2＞3（x+1），得：x＞ ， 组 为 ∴不等式 的解集 ： ＜x≤4， 选故　：A． 为应6． 了响 学校“ 香校园”建 ，阳光班的同学 书设们积 书极捐 ，其中宏志学 习组小 的同学 书别们册数分 是：5，7，x，3，4，6．已知他 平均每人捐5本， 数据的众数、中位 则这组 捐别数和方差分 是（　　） A．5，5， B．5，5，10 C．6，5.5， 【考点】方差；中位数；众数． D．5，5， 10 值义义【分析】根据平均数，可得x的 ，根据众数的定 、中位数的定 、方差的定 ，可得答 义案． 们【解答】解：由5，7，x，3，4，6．已知他 平均每人捐5本，得 x=5． 众数是5，中位数是5， 方差 = ， 选故　：D． 图别边7．如 ，D、E分 是△ABC的 AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S 则△COA=1：25， S△BDE与S△CDE的比是（　　） A．1：3 B．1：4 C．1：5 D．1：25 质【考点】相似三角形的判定与性 ．质【分析】根据相似三角形的判定定理得到△DOE∽△COA，根据相似三角形的性 定理得到 结图形得到 = ，得到答案． = ， = =， 合【解答】解：∵DE∥AC， ∴△DOE∽△COA，又S△DOE：S△COA=1：25， ∴ = ， ∵DE∥AC， ∴ = =， ∴ = ， ∴S△BDE与S△CDE的比是1：4， 选故　：B． 节8．随州市尚市“桃花 ” 观赏 门统计 约为 20万人次，20 人数逐年增加，据有关部 ，2014年 约为 设观赏 28.8万人次， 长为人数年均增 率 x， 下列方程中正确的是（　　） 则16年 A．20（1+2x）=28.8 B．28.8（1+x）2=20 C．20（1+x）2=28.8 D．20+20（1+x）+20（1+x）2=28.8 实际问题 【考点】由 【分析】 抽象出一元二次方程． 设这 观赏 长 为 人数年均增 率 x，根据“2014年 约为 约为 20万人次，2016年 28.8 两年 万人次”，可得出方程． 设观赏 2长为题人数年均增 率 x，那么依 意得20（1+x） =28.8， 【解答】解： 选故 C． 　11 图9．如 是某工件的三 视图 则积为 此工件的表面 （　　） ，A．15πcm2B．51πcm2C．66πcm2D．24πcm2 视图 【考点】由三 【分析】根据三 判断几何体． 视图 圆锥 圆锥 线长 的母 ，可得几何体是 ，根据勾股定理，可得 积 圆积 圆锥 ，根据 的面 公式，可得 ，根据扇形 积的面 公式，可得 圆锥 视图 侧积的底面 ，可得答案． 的面【解答】解：由三 ，得 ，OB=3cm，0A=4cm， 由勾股定理，得AB= =5cm， ×6π×5=15πcm2， 积面圆锥 侧的2圆锥 圆锥 积的底面 π×（ ）=9πcm， 2积的表面 15π+9π=24π（cm ）， 选故　：D． 2图 图 10．二次函数y=ax +bx+c（a≠0）的部分 象如 所示， 图过对 轴为 称象点（﹣1，0）， 线直 x=2，下列 结论 ：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣ 该图则3，y1）、点B（﹣ ，y2）、点C（ ，y3）在 函数 象上， y1＜y3＜y2；（5）若方程a 为则结论 （x+1）（x﹣5）=﹣3的两根 x1和x2，且x1＜x2， x1＜﹣1＜5＜x2．其中正确的 有（　　 ）12 A．2个 B．3个 C．4个 D．5个 图【考点】二次函数 象与系数的关系． 对轴计公式 算即可． 【分析】（1）正确．根据 称错误 时，利用x=﹣3 ，y＜0，即可判断． （2） 图（3）正确．由 象可知抛物 线经过 组（﹣1，0）和（5，0），列出方程 求出a、b即可判断 ．错误 图．利用函数 象即可判断． （4） 问题 （5）正确．利用二次函数与二次不等式关系即可解决 ．【解答】解：（1）正确．∵﹣ ∴4a+b=0．故正确． =2， 错误 时．∵x=﹣3 ，y＜0， （2） ∴9a﹣3b+c＜0， 错误 ∴9a+c＜3b，故（2） ．图（3）正确．由 象可知抛物 线经过 （﹣1，0）和（5，0）， ∴解得 ，∴8a+7b+2c=8a﹣28a﹣10a=﹣30a， ∵a＜0， ∴8a+7b=2c＞0，故（3）正确． 错误 （4） ，∵点A（﹣3，y1）、点B（﹣ ，y2）、点C（ ，y3）， ∵ ﹣2= ，2﹣（﹣ ）= ， ∴ ＜ 对轴的距离近， ∴点C离 称∴y3＞y2， ∵a＜0，﹣3＜﹣ ＜2， ∴y1＜y2 错误 ∴y1＜y2＜y3，故（4） （5）正确．∵a＜0， ．∴（x+1）（x﹣5）=﹣3/a＞0， 即（x+1）（x﹣5）＞0， 故x＜﹣1或x＞5，故（5）正确． ∴正确的有三个， 选故 B． 13 　题题题二、填空 （本大 共6个小 ，每小 3分，共18分） 题车11．2015年“圣地 都”﹣﹣随州改装 车总产值为 亿亿 14.966 元，其中14.966 元用科学 的9记为数法表示1.4966×10 　元． 记 较 【考点】科学 数法—表示 大的数． n记为为【分析】科学 数法的表示形式 a×10 的形式．其中1≤|a|＜10，n 整数，确定n的 值时变时动，要看把原数 成a ，小数点移 了多少位，n的 绝对值 动与小数点移 的位数相同．当 绝对值 时＞10 ，n是正数；当原数的 绝对值 时 负 ＜1 ，n是 数． 原数 9亿【解答】解：14.966 =1.4966×10． 9为故答案 ：1.4966×10 ． 　2边长为 边长为 则该 等腰三角形的 12．已知等腰三角形的一 长为 9，另一 方程x ﹣8x+15=0的根， 周　19或21或23　． 边【考点】解一元二次方程-因式分解法；三角形三 关系；等腰三角形的性 质．为边【分析】求出方程的解，分 两种情况，看看是否符合三角形三 关系定理，求出即可． 【解答】解：由方程x2﹣8x+15=0得：（x﹣3）（x﹣5）=0， ∴x﹣3=0或x﹣5=0， 解得：x=3或x=5， 边长为 边长为 边长为 边长为 时9、9、3 ，其周 长为 长为 当等腰三角形的三 当等腰三角形的三 当等腰三角形的三 当等腰三角形的三 21； 23； 时9、9、5 ，其周 时 边 9、3、3 ，3+3＜9，不符合三角形三 关系定理，舍去； 时9、5、5 ，其周 长为 19； 综该上， 等腰三角形的周 长为 19或21或23， 为故答案 ：19或21或23． 　图别长13．如 ，在△ABC中，∠ACB=90°，M、N分 是AB、AC的中点，延 BC至点D，使CD= BD 连则接DM、DN、MN．若AB=6， DN=　3　． ，线边线边【考点】三角形中位 定理；直角三角形斜 上的中 ；平行四 形的判定与性 ． 质14 连线证【分析】 接CM，根据三角形中位 定理得到NM= CB，MN∥BC， 明四 形DCMN是平行四 边边质 换 形，得到DN=CM，根据直角三角形的性 得到CM= AB=3，等量代 即可． 连【解答】解： 接CM， 别∵M、N分 是AB、AC的中点， ∴NM= CB，MN∥BC，又CD= BD， ∴MN=CD，又MN∥BC， 边 边 ∴四 形DCMN是平行四 形， ∴DN=CM， ∵∠ACB=90°，M是AB的中点， ∴CM= AB=3， ∴DN=3， 为故答案 ：3． 　图线线14．如 ，直 y=x+4与双曲 y= （k≠0）相交于A（﹣1，a）、B两点，在y 上找一点P 轴值 时 ，当PA+PB的 最小 ，点P的坐 标为 　（0， ）　． 问题 轴对 ；线问题 ．【考点】反比例函数与一次函数的交点 称-最短路 标【分析】根据一次函数和反比例函数的解析式求出点A、B的坐 ，然后作出点A关于y 轴的对连轴为称点C， 接BC，与y 的交点即 点P，然后求出直 BC的解析式，求出点P的坐 ． 线标标【解答】解：把点A坐 代入y=x+4得， ﹣1+4=a， a=3， 即A（﹣1，3）， 标 线 把点A坐 代入双曲 的解析式：3=﹣k， 解得：k=﹣3， 15 联立两函数解析式得： ，解得： ，，标为 即点B坐 ：（﹣3，1）， 轴对连轴为值作出点A关于y 的称点C， 接BC，与y 的交点即 点P，使得PA+PB的 最小， 标为 ：（1，3）， 则设点C坐 线 为 直 BC的解析式 ：y=ax+b， 标把B、C的坐 代入得： ，解得： ，为函数解析式 ：y= x+ ， 则轴 为 与y 的交点 ：（0， ）． 为故答案 ：（0， ）． 　图 证 15．如 （1），PT与⊙O1相切于点T，PAB与⊙O1相交于A、B两点，可 明△PTA∽△PBT， 2请应 结论 问题 图别 ：如 （2），PAB、PCD分 与⊙O2相交 从而有PT =PA•PB． 用以上 解决下列 则于A、B、C、D四点，已知PA=2，PB=7，PC=3， CD=　． 质线质【考点】相似三角形的判定与性 ；切 的性 ． 2图过线【分析】如 2中， 点P作⊙O的切 PT，切点是T，根据PT =PA•PB=PC•PD，求出PD即可解 问题 决．图过线【解答】解：如 2中， 点P作⊙O的切 PT，切点是T． 16 ∵PT2=PA•PB=PC•PD， ∵PA=2，PB=7，PC=3， ∴2×7=3×PD， ∴PD= ∴CD=PD﹣PC= ﹣3=． 　图边长为 对线 顶 1的正方形ABCD的 角 AC、BD相交于点O．有直角∠MPN，使直角 点P 16．如 ，边 别 与点O重合，直角 PM、PN分 与OA、OB重合，然后逆 时针 转转为角 θ（0°＜ 旋∠MPN，旋 别连则结论 中正确的 θ＜90°），PM、PN分 交AB、BC于E、F两点， 接EF交OB于点G， 下列 是　（1），（2），（3），（5）　． 转过 （1）EF= OE；（2）S四 形OEBF：S正方形ABCD=1：4；（3）BE+BF= OA；（4）在旋 边程中 22积 时 ，当△BEF与△COF的面 之和最大 ，AE= ；（5）OG•BD=AE +CF ． 边综题．【考点】四 【分析】（1）由四 形ABCD是正方形，直角∠MPN，易 得△BOE≌△COF（ASA）， 结论 形合边证则证可得；证（2）由（1）易 得S四 形OEBF=S△BOC= S正方形ABCD 边则证结论 得 ； ，可质证得BE+BF= OA； （3）由BE=CF，可得BE+BF=BC，然后由等腰直角三角形的性 ，设则继（4）首先 AE=x， BE=CF=1﹣x，BF=x， 而表示出△BEF与△COF的面 之和，然后利用 积值问题 二次函数的最 ，求得答案； （5）易 得△OEG∽△OBE，然后由相似三角形的 结论 2证对应边 证成比例， 得OG•OB=OE ，再利用O 证B与BD的关系，OE与EF的关系，即可 得．边【解答】解：（1）∵四 形ABCD是正方形， ∴OB=OC，∠OBE=∠OCF=45°，∠BOC=90°， ∴∠BOF+∠COF=90°， ∵∠EOF=90°， ∴∠BOF+∠COE=90°， ∴∠BOE=∠COF， 在△BOE和△COF中， ，∴△BOE≌△COF（ASA）， 17 ∴OE=OF，BE=CF， ∴EF= OE；故正确； （2）∵S四 形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC= S正方形ABCD 边，∴S四 形OEBF：S正方形ABCD=1：4；故正确； 边（3）∴BE+BF=BF+CF=BC= OA；故正确； 过（4） 点O作OH⊥BC， ∵BC=1， ∴OH= BC= ， 设则AE=x， BE=CF=1﹣x，BF=x， ∴S△BEF+S△COF= BE•BF+ CF•OH= x（1﹣x）+ （1﹣x）× =﹣ （x﹣ ）2+ ∵a=﹣ ＜0， ，时∴当x= ，S△BEF+S△COF最大； 转过 积时程中，当△BEF与△COF的面 之和最大 ，AE= ；故 ； 错误 即在旋 （5）∵∠EOG=∠BOE，∠OEG=∠OBE=45°， ∴△OEG∽△OBE， ∴OE：OB=OG：OE， ∴OG•OB=OE2， ∵OB= BD，OE= EF， ∴OG•BD=EF2， ∵在△BEF中，EF2=BE2+BF2， ∴EF2=AE2+CF2， ∴OG•BD=AE2+CF2．故正确． 为故答案 ：（1），（2），（3），（5）． 　题题题应骤说三、解答 （本 共9小 ，共72分，解答 写出必要演算步 ，文字 明或 证过明 程） 18 •cos30°﹣（﹣ ）﹣2+（π﹣3.14）0． 计17． 算：﹣|﹣1|+ 实【考点】 数的运算；零指数 幂负幂 值 整数指数 ；特殊角的三角函数 ． ；题【分析】本 涉及 绝对值 简、二次根式化 、特殊角的三角函数 值负 幂幂 指数 、零指数 5个 、计时针对 别进 计实 则 算，然后根据 数的运算法 求得 计结算考点．在 果． 算，需要 每个考点分 行【解答】解：原式=﹣1+2 × ﹣4+1 =﹣1+3﹣4+1 =﹣1． 　简 值 18．先化 ，再求 ：（ ﹣x+1）÷ ，其中x= ﹣2． 简值．【考点】分式的化 求转为 简值 乘法，化 后代入x的 即可求解 【分析】首先将括号里面的通分相减，然后将除法 ．化【解答】解：原式=[ ﹣]• ==•，时当x= ﹣2 原式= ，==2 ．　时间 观骑车过19．某校学生利用双休 了20min后，其余学生乘汽 沿相同路 骑车 去距学校10km的炎帝故里参 ，一部分学生 自行 先走， 车线发结们时 车 到达．已知汽 的速度是 骑车 出，果他 同车学生速度的2倍，求 学生的速度和汽 的速度． 应【考点】分式方程的 用． 时间 键来列等量关系．关 描述 语为 骑：“一部分学生 自 【分析】求速度，路程已知，根据 车过 车 先走， 了20min后，其余学生乘汽 沿相同路 线发结们时行出，果他 同到达”，根据等 量关系列出方程． 设骑车 为时车学生的速度 x千米/小 ，汽 的速度 2x千米/小 为时【解答】解： 可得： ，，解得：x=15， 经检验 x=15是原方程的解， 2x=2×15=30， 骑车 车 别时 学生的速度和汽 的速度分 是每小 15km，30km． 答： 　务办厅发总公 2015年3月16日 布了《中国足球改革的 体方案》， 是中国足球 史 这历20．国 院为进识传 举进 播足球文化，我市 行了“足球 校园”知 上的重大改革． 了一步普及足球知 ，19 识竞赛 动为识了解足球知 的普及情况，随机抽取了部分 获奖 进 情况 行整理，得到下列 活，统计图 不完整的 表： 获奖 频频率等次 数奖奖奖一等 10 0.05 0.10 b二等 三等 20 30 a优胜奖 0.30 0.40 奖鼓励 80 请给根据所 信息，解答下列 问题 ：补频图数分布直方 ； （1）a=　60　，b=　0.15　，且 全统计图 获奖 问获 优胜奖对应圆 的扇形 心角的度数是多少 （2）若用扇形 来描述 选中，甲、乙、丙、丁四位同学都 得一等 ，若从 四位同学中随机 取 分布情况， 得？这竞赛 获奖这（3）在 次级竞赛 请树图 计选 或列表的方法， 算恰好 中甲、乙二人 两位同学代表我市参加上一 的概率． ，用状树图频频法； 数（率）分布表； 数（率）分布直方 ；扇形 图统计图 【考点】列表法与 状．频 频 【分析】（1）根据公式 率= 数÷ 样总样总值本数，求得 本数，再根据公式得出a，b的 即可； 优胜奖对应 圆的扇形 心角的度数= 优胜奖 频计率×360° 算即可； （2）根据公式 的树图 结举 或列表将所有等可能的 果列 出来，利用概率公式求解即可． （3）画 状样总为数 10÷0.05=200人， 【解答】解：（1） 本a=200﹣10﹣20﹣30﹣80=60人， b=30÷200=0.15， 为故答案 200，0.15； 优胜奖 圆 为 所在扇形的 心角 0.30×360°=108°； （2） 别（2）列表：甲乙丙丁分 用ABCD表示， ABCDAAB AC AD BC BD B BA C CA CB CD D DA DB DC 结 选 ∵共有12种等可能的 果，恰好 中A、B的有2种， 树图如下： 画状20 选∴P（ 中A、B）= =． 　兴 组 21．某班数学 趣小 利用数学活 动课时间测 顶量位于烈山山 的炎帝雕像高度，已知烈山 夹 为 坡面与水平面的 角 30°，山高857.5尺， 组员 处 进 从山脚D 沿山坡向着雕像方向前 1620 处测 顶 为 得雕像 端A的仰角 60°，求雕像AB的高度． 尺到达E点，在点E 应【考点】解直角三角形的 用-仰角俯角 问题 ．锐【分析】构造直角三角形，利用 角三角函数， 进简单计 行 算即可． 图【解答】解：如 ，过点E作EF⊥AC，EG⊥CD， 在Rt△DEG中，∵DE=1620，∠D=30°， ∴EG=DEsin∠D=1620× =810， ∵BC=857.5，CF=EG， ∴BF=BC﹣CF=47.5， 在Rt△BEF中，tan∠BEF= ∴EF= BF， ，设在Rt△AEF中，∠AEF=60°， AB=x， ∵tan∠AEF= ∴AF=EF×tan∠AEF， ，21 ∴x+47.5=3×47.5， ∴x=95， 为答：雕像AB的高度 95尺． 　图为过22．如 ，AB是⊙O的弦，点C 半径OA的中点， 点C作CD⊥OA交弦AB于点E， 接BD，且D 连E=DB． 说（1）判断BD与⊙O的位置关系，并 明理由； （2）若CD=15，BE=10，tanA= ，求⊙O的直径． 线圆质．【考点】直 与的位置关系；垂径定理；相似三角形的判定与性 连圆证【分析】（1） 接OB，由 的半径相等和已知条件 明∠OBD=90°，即可 明BD是⊙O的 证线切；过 质 （2） 点D作DG⊥BE于G，根据等腰三角形的性 得到EG= BE=5，由两角相等的三角形相 对应 似，△ACE∽△DGE，利用相似三角形 角相等得到sin∠EDG=sinA= ，在Rt△EDG中， 长 结 利用勾股定理求出DG的 ，根据三角形相似得到比例式，代入数据即可得到 果． 证 连 【解答】（1） 明： 接OB， ∵OB=OA，DE=DB， ∴∠A=∠OBA，∠DEB=∠ABD， 又∵CD⊥OA， ∴∠A+∠AEC=∠A+∠DEB=90°， ∴∠OBA+∠ABD=90°， ∴OB⊥BD， 线∴BD是⊙O的切 ；图（2）如 ∵DE=DB， 过点D作DG⊥BE于G， ，∴EG= BE=5， ∵∠ACE=∠DGE=90°，∠AEC=∠GED， ∴∠GDE=∠A， ∴△ACE∽△DGE， ∴sin∠EDG=sinA= = ，即CE=13， 在Rt△ECG中， ∵DG= =12， ∵CD=15，DE=13， 22 ∴DE=2， ∵△ACE∽△DGE， ∴ = ，∴AC= •DG= ，∴⊙O的直径2OA=4AD= ．　级 兴 23．九年 （3）班数学 趣小 组经过 场调查 市为整理出某种商品在第x天（1≤x≤90，且x 设该 为 销进为整数）的售价与 售量的相关信息如下．已知商品的 价 30元/件， 商品的售价 y 单销为单销位：元/件），每天的 售量 p（ 位：件），每天的 售利 润为 单w（ 位：元）． （时间 x（天） 130 60 90 销每天 售量p（件 198 140 80 20 ）（1）求出w与x的函数关系式； 问销 该时销润商品第几天 ，当天的 售利 最大？并求出最大利 ； 润（2） 售该（3） 商品在 销过 销润 请结 程中，共有多少天每天的 售利 不低于5600元？ 直接写出 果． 售应应【考点】二次函数的 用；一元一次不等式的 用． 时间 为 x的函数关系式 y=kx+b，由点的坐 时设【分析】（1）当0≤x≤50 ，商品的售价y与 标时图利用待定系数法即可求出此 y关于x的函数关系式，根据 形可得出当50＜x≤90 ，y= 时结给设 销 定表格， 每天的 售量p与 时间 为 x的函数关系式 p=mx+n，套入数据利用待 90．再 合销润 单 润定系数法即可求出p关于x的函数关系式，根据 售利 = 件利 × 售数量即可得出w关 销于x的函数关系式； 虑值问题 时结合二次函数的性 （2）根据w关于x的函数关系式，分段考 其最 ．当0≤x≤50 即可求出在此范 内w的最大 ；当50＜x≤90 ，根据一次函数的性 即可求出在此范 结论 ，质围围值时质值值较内w的最大 ，两个最大 作比 即可得出 ；（3）令w≥5600，可得出关于x的一元二次不等式和一元一次不等式，解不等式即可得出x 结论 值围，由此即可得出 的取 范．时设时间 为为 x的函数关系式 y=kx+b（k、b 【解答】解：（1）当0≤x≤50 常数且k≠0）， ，商品的售价y与 23 经过 ∵y=kx+b ∴点（0，40）、（50，90）， ，解得： ，时间 为x的函数关系式 y=x+40； ∴售价y与 时当50＜x≤90 ，y=90． 时间 为x的函数关系式 y= ∴售价y与 ．书记 销可知每天的 售量p与 时间 x成一次函数关系， 由设销每天的 售量p与 时间 为 为 x的函数关系式 p=mx+n（m、n 常数，且m≠0）， 过∵p=mx+n 点（60，80）、（30，140）， ，解得： ∴p=﹣2x+200（0≤x≤90，且x 整数）， ∴，为2时当0≤x≤50 ，w=（y﹣30）•p=（x+40﹣30）（﹣2x+200）=﹣2x +180x+2000； 时当50＜x≤90 ，w=（90﹣30）（﹣2x+200）=﹣120x+12000． 综销润上所示，每天的 售利 w与 x的函数关系式是w= 时间 ．22时（2）当0≤x≤50 ，w=﹣2x +180x+2000=﹣2（x﹣45） +6050， ∵a=﹣2＜0且0≤x≤50， 时 值 ∴当x=45 ，w取最大 ，最大 值为 6050元． 时当50＜x≤90 ，w=﹣120x+12000， ∵k=﹣120＜0，w随x增大而减小， 时 值 ∴当x=50 ，w取最大 ，最大 值为 6000元． ∵6050＞6000， 时∴当x=45 ，w最大，最大 值为 6050元． 销时 获销 润润 售第45天 ，当天 得的 售利 最大，最大利 是6050元． 即22时（3）当0≤x≤50 ，令w=﹣2x +180x+2000≥5600，即﹣2x +180x﹣3600≥0， 解得：30≤x≤50， 50﹣30+1=21（天）； 时当50＜x≤90 ，令w=﹣120x+12000≥5600，即﹣120x+6400≥0， 解得：50＜x≤53 ， 为∵x 整数， ∴50＜x≤53， 53﹣50=3（天）． 综故　上可知：21+3=24（天）， 该销过销润商品在 售程中，共有24天每天的 售利 不低于5600元． 查阅资 发现 了“中垂三角形”，即 爱线时料 ， 24． 好思考的小茜在探究两条直 的位置关系 线为图图两条中 互相垂直的三角形称 “中垂三角形”．如 （1）、 （2）、 （3）中，AM、 图24 线BN是△ABC的中 ，AN⊥BN于点P，像△ABC 这样 为 设 的三角形均 “中垂三角形”． BC=a，AC =b，AB=c． 【特例探究】 图（1）如 1，当tan∠PAB=1，c=4 时，a=　4 　，b=　4 　； 图 时 如 2，当∠PAB=30°，c=2 ，a=　，b=　； 归纳证 【明】 222请观计结 间 果，猜想a 、b 、c 三者之 的关系，用等式表示出来，并 （2） 你察（1）中的 结论 算图 证 利用 3 明你的 ．证【拓展 明】 图别连（3）如 4，▱ABCD中，E、F分 是AD、BC的三等分点，且AD=3AE，BC=3BF， 接AF、BE、 长CE，且BE⊥CE于E，AF与BE相交点G，AD=3 ，AB=3，求AF的 ．边综题．【考点】四 【分析】（1）①首先 明△APB，△PEF都是等腰直角三角形，求出PA、PB、PE、PF，再利 问题 形合证用勾股定理即可解决 ．连质接EF，在RT△PAB，RT△PEF中，利用30°性 求出PA、PB、PE、PF，再利用勾股定理 ②问题 即可解决 ．222222结论 设则a +b =5c ． MP=x，NP=y， AP=2x，BP=2y，利用勾股定理分 求出a 、b 、c 别（2） 问题 即可解决 ．连 长 （3）取AB中点H， 接FH并且延 交DA的延 长线 证于P点，首先 明△ABF是中垂三角形，利 结论 问题 列出方程即可解决 用（2）中 ．图【解答】（1）解：如 1中，∵CE=AE，CF=BF， ∴EF∥AB，EF= AB=2 ∵tan∠PAB=1， ，∴∠PAB=∠PBA=∠PEF=∠PFE=45°， ∴PF=PE=2，PB=PA=4， ∴AE=BF= =2 ．∴b=AC=2AE=4 ，a=BC=4 ．为故答案 4 ，4 ．图 连 如 2中， 接EF， ，∵CE=AE，CF=BF， ∴EF∥AB，EF= AB=1， ∵∠PAB=30°， ∴PB=1，PA= ，在RT△EFP中，∵∠EFP=∠PAB=30°， 25 ∴PE= ，PF= ，∴AE= =，BF= =，∴a=BC=2BF= ，b=AC=2AE= ，别为 故答案分 ，．222结论 （2） a +b =5c ． 证图 连 明：如 3中， 接EF． 线∵AF、BE是中 ，∴EF∥AB，EF= AB， ∴△FPE∽△APB， ∴ = =， 设则FP=x，EP=y， AP=2x，BP=2y， ∴a2=BC2=4BF2=4（FP2+BP2）=4×2+16y2， b2=AC2=4AE2=4（PE2+AP2）=4y2+16×2， c2=AB2=AP2+BP2=4×2+4y2， ∴a2+b2=20×2+20y2=5（4×2+4y2）=5c2． 图（3）解：如 4中，在△AGE和△FGB中， ，∴△AGE≌△FGB， 连长长线 ∴BG=FG，取AB中点H， 接FH并且延 交DA的延 于P点， 证同理可 △APH≌△BFH， ∴AP=BF，PE=CF=2BF， 即PE∥CF，PE=CF， 边 边 ∴四 形CEPF是平行四 形， ∴FP∥CE， ∵BE⊥CE， ∴FP⊥BE，即FH⊥BG， ∴△ABF是中垂三角形， 由（2）可知AB2+AF2=5BF2， ∵AB=3，BF= AD= ，∴9+AF2=5×（ ）2， ∴AF=4． 26 　线 轴 25．已知抛物 y=a（x+3）（x﹣1）（a≠0），与x 从左至右依次相交于A、B两点，与y 轴经过 线线为相交于点C， （1）若点D的横坐 （2）若在第三象限内的抛物 上有点P，使得以A、B、P 点A的直 y=﹣ x+b与抛物 的另一个交点 D． 标为 线2，求抛物 的函数解析式； 线为顶 点的三角形与△ABC相似，求 标点P的坐 ；设线连（3）在（1）的条件下， 点E是 段AD上的一点（不含端点）， 接BE．一 点Q从点B出 动发线单动线单动，沿 段BE以每秒1个 位的速度运 到点E，再沿 段ED以每秒 位的速度运 动过 时间 程中所用 最少？ 个问标时到点D后停止， 当点E的坐 是多少 ，点Q在整个运 综题．【考点】二次函数 合标 线 【分析】（1）根据二次函数的交点式确定点A、B的坐 ，求出直 的解析式，求出点D的 标线，求出抛物 的解析式； 坐27 轴 设 （2）作PH⊥x 于H， 点P的坐 标为 （m，n），分△BPA∽△ABC和△PBA∽△ABC，根据相 质计 似三角形的性 算即可； 轴线轴义（3）作DM∥x 交抛物 于M，作DN⊥x 于N，作EF⊥DM于F，根据正切的定 求出Q的运 动时间 时t=BE+EF ，t最小即可． 【解答】解：（1）∵y=a（x+3）（x﹣1）， 标为 标为 （1，0）， ∴点A的坐 （﹣3，0）、点B两的坐 线经过 ∵直 y=﹣ x+b ∴b=﹣3 ∴y=﹣ x﹣3 点A， ，，，时当x=2 ，y=﹣5 则标为 点D的坐 （2，﹣5 ）， 线∵点D在抛物 上， ∴a（2+3）（2﹣1）=﹣5 ，解得，a=﹣ ，抛物 的解析式 y=﹣ （x+3）（x﹣1）=﹣ x2﹣2 x+3 ；则线为轴（2）作PH⊥x 于H， 设标为 点P的坐 （m，n）， 时当△BPA∽△ABC ，∠BAC=∠PBA， ∴tan∠BAC=tan∠PBA，即 = ，∴∴=，即n=﹣a（m﹣1）， ，题解得，m1=﹣4，m2=1（不合 意，舍去）， 时当m=﹣4 ，n=5a， ∵△BPA∽△ABC， ∴ = ，即AB2=AC•PB， ∴42= •，题（不合 意，舍去），a2=﹣ 解得，a1= ，则n=5a=﹣ ，标为 ∴点P的坐 当△PBA∽△ABC ，∠CBA=∠PBA， ∴tan∠CBA=tan∠PBA，即 = ，即n=﹣3a（m﹣1）， （﹣4，﹣ ）； 时，∴=28 ∴，题解得，m1=﹣6，m2=1（不合 意，舍去）， 时当m=﹣6 ，n=21a， ∵△PBA∽△ABC， ∴ = ，即AB2=BC•PB， ∴42= •，题（不合 意，舍去），a2=﹣ 解得，a1= ，则综标为 点P的坐 （﹣6，﹣ ）， 标为 上所述，符合条件的点P的坐 （﹣4，﹣ ）和（﹣6，﹣ ）； 轴线轴（3）作DM∥x 交抛物 于M，作DN⊥x 于N，作EF⊥DM于F， 则tan∠DAN= = =，∴∠DAN=60°， ∴∠EDF=60°， ∴DE= =EF， 动时间 ∴Q的运 t= + =BE+EF， 线时 ∴当BE和EF共 ，t最小， 则BE⊥DM，y=﹣4 ．29 　30