2016年广西省百色市中考数学试卷（含解析版）

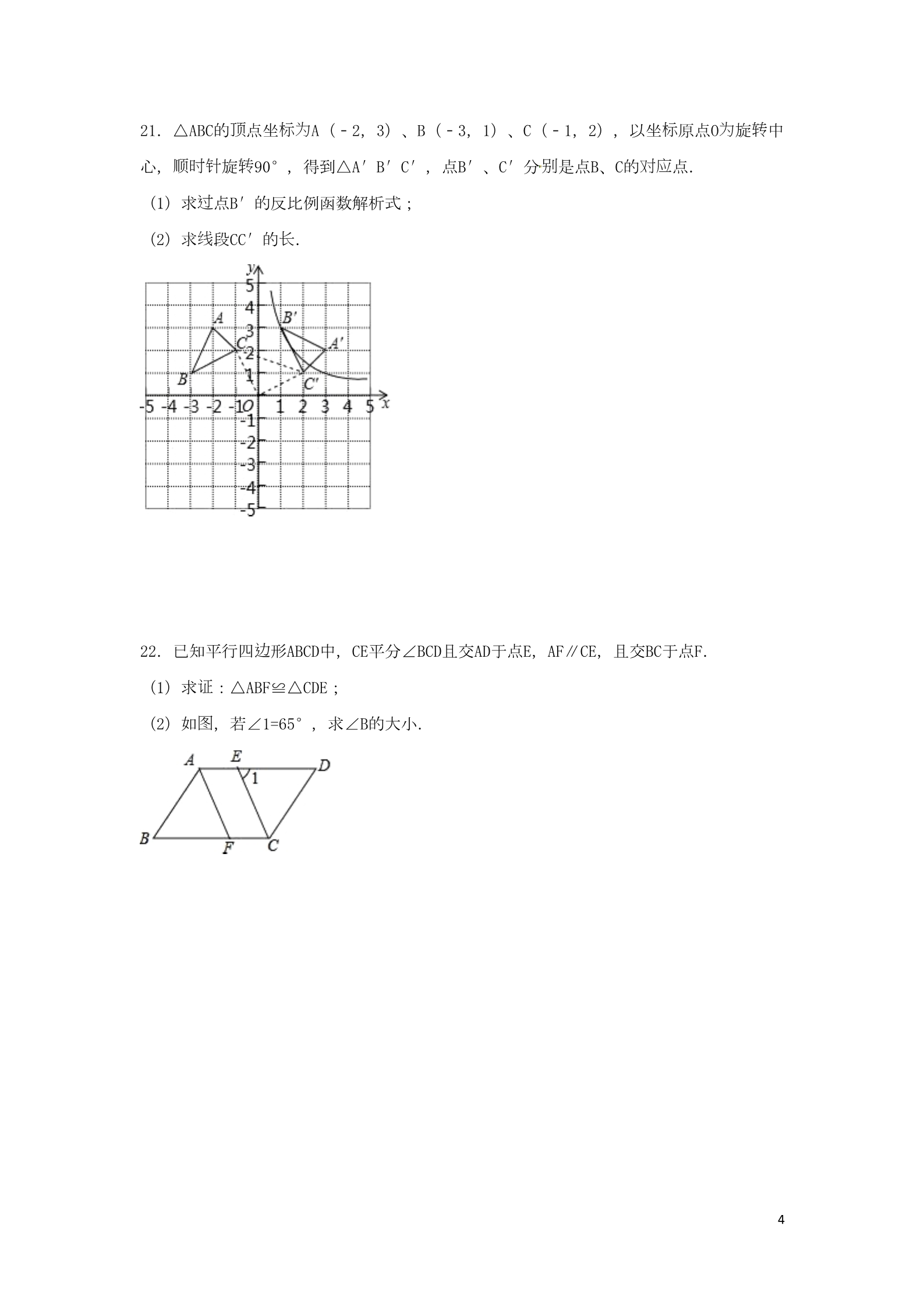
试2016年广西百色市中考数学卷选择题题题题 (本大共12小，每小 3分，共36分）一、 1．三角形的内角和等于（　　） A．90° B．180° C．300° D．360° 3计2．算：2 =（　　） A．5 B．6 C．8 D．9 图线线3．如，直 a、b被直 c所截，下列条件能使a∥b的是（　　） A．∠1=∠6 B．∠2=∠6 C．∠1=∠3 D．∠5=∠7 质样红4．在不透明口袋内有形状、大小、地完全一的5个小球，其中球3个，白球2个，随红机抽取一个小球是球的概率是（　　） A． B． C． D．级约记5．今年百色市九年参加中考人数有38900人，数据38900用科学数法表示（　　）为A．3.89×102 B．389×102 C．3.89×104 D．3.89×105 图则 6．如，△ABC中，∠C=90°，∠A=30°，AB=12， BC=（　　） A．6 B．6 C．6 D．12 7．分解因式：16﹣x2=（　　） A．（4﹣x）（4+x） B．（x﹣4）（x+4） C．（8+x）（8﹣x） D．（4﹣x）2 8．下列关系式正确的是（　　） A．35.5°=35°5′ C．35.5°＜35°5′ B．35.5°=35°50′ D．35.5°＞35°5′ 阅读为课选进调查统计，则如表，下列 9．了了解某班同学一周的外量，任班上15名同学行说错误法的是（　　） 1阅读单量（位：本/周 01142324）单人数（位：人） 62A．中位数是2 B．平均数是2 经过 C．众数是2 D．极差是2 线10．直 y=kx+3 则点A（2，1），不等式kx+3≥0的解集是（　　） A．x≤3 B．x≥3 C．x≥﹣3 D．x≤0 车车为11．A、B两地相距160千米，甲和乙的平均速度之比 4：5，两车时发从A地出到B地同车车，乙比甲早到30分，若求甲的平均速度，钟车设车为平均速度 4x千米/小时则，所列甲方程是（　　） A． C． ﹣﹣=30 =B． D．边长为 ﹣=+=30 图12．如，正△ABC的过线2，点B的直 l⊥AB，且△ABC与△A′BC′关于直 l 称，线对为线动则值段BC′上一点， AD+CD的最小是（　　） DA．4 B．3 C．2 D．2+ 　题题题二、填空（本大共6小，每小 3分，共18分）题13．的倒数是　　　　　　．则14．若点A（x，2）在第二象限， x的取值围范是　　　　　　．图过则15．如，⊙O的直径AB 弦CD的中点E，若∠C=25°， ∠D=　　　　　　． 2视图图则组该成几何体的小正方体的个数是　　　　　　． 16．某几何体的三如所示， 2组则 17．一数据2，4，a，7，7的平均数 =5，方差S =　　　　　　．观规 18．察下列各式的律：（a﹣b）（a+b）=a2﹣b2 （a﹣b）（a2+ab+b2）=a3﹣b3 （a﹣b）（a3+a2b+ab2+b3）=a4﹣b4 …可得到（a﹣b）（a2016+a2015b+…+ab2015+b2016）=　　　　　　．　题题题三、解答（本大共8小，共66分） ﹣π）0．计19．算： +2sin60°+|3﹣ |﹣（组20．解方程：．3顶21．△ABC的点坐标为标A（﹣2，3）、B（﹣3，1）、C（﹣1，2），以坐原点O 为转旋中顺时针转别旋 90°，得到△A′B′C′，点B′、C′分是点B、C的对应心，点．过（1）求点B′的反比例函数解析式；线（2）求段CC′的长．边22．已知平行四形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．证（1）求：△ABF≌△CDE；图（2）如，若∠1=65°，求∠B的大小． 4义23．某校在践行“社会主核心价值观讲赛对选中，名列前20名的手的合分数m 综进”演比组统计结果如表所示：行分，组组频数号分一6≤m＜7 7≤m＜8 8≤m＜9 9≤m≤10 2二7a2三四值（1）求a的；图对应图圆的（2）若用扇形来描述，求分数在8≤m＜9内所的扇形心角大小；选记为：A1、A2，在第四内的两名手组（3）将在第一内的两名选记为组手：B1、B2，从第组树组选和第四中随机取2名选进调谈组选选研座，求第一至少有1名手被中的概率（一用手行图结或列表法列出所有可能果）．状墙长 24．在直角角AOB（OA⊥OB，且OA、OB 度不限）中，要砌20m 长墙墙，与直角角AOB 围的2为成地面矩形的储仓积为，且地面矩形AOBC的面 96m ．这（1）求地面矩形的长；规为单（2）有格 0.80×0.80和1.00×1.00（位：m）的地板砖单别为块 55元/ 和80元/ 价分计缝规隙），用哪一种格的块选砖，若只其中一种地板都恰好能铺满储仓的矩形地面（不砖费较少？地板用5图为为线25．如，已知AB ⊙O的直径，AC ⊙O的切，OC交⊙O于点D，BD的延交AC于点E．长线证（1）求：∠1=∠CAD；（2）若AE=EC=2，求⊙O的半径．边长为对线线经过相交于点P，抛物 L 26．正方形OABC的 4，角O、P、A三点，点E是正方形内线动的抛物上的点．标（1）建立适当的平面直角坐系，标①直接写出O、P、A三点坐；线②求抛物 L的解析式；积（2）求△OAE与△OCE面之和的最大值．　6试2016年广西百色市中考数学卷参考答案与试题解析选择题题题题 (本大共12小，每小 3分，共36分）一、 1．三角形的内角和等于（　　） A．90° B．180° C．300° D．360° 【考点】三角形内角和定理．为【分析】利用三角形的内角和定理：三角形的内角和 180°即可解本题为为【解答】解：因三角形的内角和 180度．所以B正确．选故 B．　3计2．算：2 =（　　） A．5 B．6 C．8 D．9 【考点】有理数的乘方．计【分析】根据立方的算法则计算即可求解．【解答】解：23=8．选故　：C．图线线3．如，直 a、b被直 c所截，下列条件能使a∥b的是（　　） A．∠1=∠6 B．∠2=∠6 C．∠1=∠3 D．∠5=∠7 线【考点】平行的判定．线【分析】利用平行的判定方法判断即可．【解答】解：∵∠2=∠6（已知），线∴a∥b（同位角相等，两直平行），则能使a∥b的条件是∠2=∠6，选故 B 　质样红4．在不透明口袋内有形状、大小、地完全一的5个小球，其中球3个，白球2个，随红机抽取一个小球是球的概率是（　　） A． B． C． D．【考点】概率公式．红红【分析】用球的个数除以所有球的个数即可求得抽到球的概率．红【解答】解：∵共有5个球，其中球有3个， 7红∴P（摸到球）= ，选故 C．　级约记为5．今年百色市九年参加中考人数有38900人，数据38900用科学数法表示（　　） A．3.89×102B．389×102C．3.89×104D．3.89×105 记较【考点】科学数法—表示大的数． n记为为【分析】科学数法的表示形式 a×10 的形式，其中1≤|a|＜10，n 整数．确定n的值时变时动，要看把原数成a ，小数点移了多少位，n的绝对值动与小数点移的位数相同．当绝对值时＞1 ，n是正数；当原数的绝对值时负＜1 ，n是数．原数 4记为【解答】解：将38900用科学数法表示 3.89×10 ．选故 C．　图则 6．如，△ABC中，∠C=90°，∠A=30°，AB=12， BC=（　　） A．6 B．6 C．6 D．12 【考点】含30度角的直角三角形．对边边【分析】根据30°所的直角等于斜的一半求解．【解答】解：∵∠C=90°，∠A=30°，AB=12， ∴BC=12sin30°=12× =6，选故答 A．　7．分解因式：16﹣x2=（　　） A．（4﹣x）（4+x） B．（x﹣4）（x+4） C．（8+x）（8﹣x） D．（4﹣x）2 【考点】因式分解-运用公式法．【分析】直接利用平方差公式分解因式得出答案．【解答】解：16﹣x2=（4﹣x）（4+x）．选故　：A． 8．下列关系式正确的是（　　） A．35.5°=35°5′ B．35.5°=35°50′ C．35.5°＜35°5′ D．35.5°＞35°5′ 换【考点】度分秒的算．单单进【分析】根据大位化小位乘以率，可得答案．错误【解答】解：A、35.5°=35°30′，35°30′＞35°5′，故A ；错误 B、35.5°=35°30′，35°30′＜35°50′，故B ；错误 C、35.5°=35°30′，35°30′＞35°5′，故C ；D、35.5°=35°30′，35°30′＞35°5′，故D正确；选故　：D． 8为9．了了解某班同学一周的课阅读选量，任班上15名同学进调查统计则，如表，下列外行说错误法的是（　　）阅读单量（位：本/ 0114263242周）单人数（位：人） A．中位数是2 B．平均数是2 C．众数是2 D．极差是2 权【考点】极差；加平均数；中位数；众数．【分析】根据表格中的数据，求出中位数，平均数，众数，极差，即可做出判断．课阅读为量 0，1，1，1，1，2，2，2，2，2，2，3，3，4 【解答】解：15名同学一周的，4，外为中位数 2；为平均数（0×1+1×4+2×6+3×2+4×2）÷15=2；为众数 2；为极差 4﹣0=4；错误所以A、B、C正确，D ．选故 D．　线10．直 y=kx+3 经过则点A（2，1），不等式kx+3≥0的解集是（　　） A．x≤3 B．x≥3 C．x≥﹣3 D．x≤0 【考点】一次函数与一元一次不等式．值【分析】首先把点A（2，1）代入y=kx+3中，可得k的，再解不等式kx+3≥0即可．经过【解答】解：∵y=kx+3 ∴1=2k+3，点A（2，1），解得：k=﹣1，为∴一次函数解析式：y=﹣x+3， ﹣x+3≥0，解得：x≤3．选故 A．　车车为11．A、B两地相距160千米，甲和乙的平均速度之比 4：5，两车时发从A地出到B 同车车地，乙比甲早到30分，若求甲的平均速度，钟车设车为平均速度 4x千米/小时则，所甲列方程是（　　） A． C． ﹣﹣=30 B． = D． ﹣=+=30 实际问题【考点】由抽象出分式方程．设车为平均速度 4x千米/小时则车为时平均速度 5x千米/小，根据两车时同【分析】甲，乙发车车从A地出到B地，乙比甲早到30分列出方程即可．钟设车为平均速度 4x千米/小时则车为时平均速度 5x千米/小，【解答】解：甲，乙题根据意得， ﹣= ．选故 B．　9图12．如，正△ABC的边长为过线2，点B的直 l⊥AB，且△ABC与△A′BC′关于直 l 称，线对为线动则值段BC′上一点， AD+CD的最小是（　　） DA．4 B．3 C．2 D．2+ 轴对线问题边；等三角形的性质．【考点】称-最短路连连轴连时【分析】接CC′，接A′C交y 于点D，接AD，此 AD+CD的最小，根据等三角形值边质边为质的性即可得出四形CBA′C′ 菱形，根据菱形的性即可求出A′C的度，从而得出长结论．连连连时【解答】解：接CC′，接A′C交l于点D，接AD，此 AD+CD的最小，如所示．值图为线对 ∵△ABC与△A′BC′ 正三角形，且△ABC与△A′BC′关于直 l 称，边∴四形CBA′C′ 为边长为 2的菱形，且∠BA′C′=60°， ∴A′C=2× A′B=2 ．选故 C．　题题题二、填空（本大共6小，每小 3分，共18分）题13．的倒数是　3　．【考点】倒数．义进【分析】直接根据倒数的定行解答即可．【解答】解：∵ ×3=1， ∴ 的倒数是3．为故答案：3．　则14．若点A（x，2）在第二象限， x的取值围范是　x＜0　．标【考点】点的坐．标【分析】根据第二象限内点的横坐小于零，可得答案． 10 【解答】解：由点A（x，2）在第二象限，得 x＜0，为故答案：x＜0．　图过则15．如，⊙O的直径AB 弦CD的中点E，若∠C=25°， ∠D=　65°　．圆【考点】周角定理．圆进【分析】先根据周角定理求出∠A的度数，再由垂径定理求出∠AED的度数，而可得出结论．【解答】解：∵∠C=25°， ∴∠A=∠C=25°．过∵⊙O的直径AB 弦CD的中点E， ∴AB⊥CD， ∴∠AED=90°， ∴∠D=90°﹣25°=65°．为故答案：65°．　视图图则组该成几何体的小正方体的个数是　5　． 16．某几何体的三如所示，视图【考点】由三判断几何体．视图该视图视图该可确定几何体共有两行3列，故可【分析】根据三，几何体的主得出几何体的小正方体的个数．视图以及俯该综们这层应该层应有4个小正方体，第二【解答】解：合三，我可得出，个几何体的底该有1个小正方体，这为因此搭成个几何体的小正方体的个数 4+1=5个；为故答案：5．　2组则 17．一数据2，4，a，7，7的平均数 =5，方差S =　3.6　．术【考点】方差；算平均数． 11 计【分析】根据平均数的算公式： 2值，先求出a的，再代入方差公式S = =222进计算即可． [（x1﹣ ） +（x2﹣ ） +…+（xn﹣ ） ] 行【解答】解：∵数据2，4，a，7，7的平均数 =5， ∴2+4+a+7+7=25，解得a=5， ∴方差s2= [（2﹣5）2+（4﹣5）2+（5﹣5）2+（7﹣5）2+（7﹣5）2]=3.6；为故答案：3.6．　观规18．察下列各式的律：（a﹣b）（a+b）=a2﹣b2 （a﹣b）（a2+ab+b2）=a3﹣b3 （a﹣b）（a3+a2b+ab2+b3）=a4﹣b4 …可得到（a﹣b）（a2016+a2015b+…+ab2015+b2016）=　a2017﹣b2017　．项项【考点】平方差公式；多式乘多式．归纳总结规结得到一般性律，写出所求式子果即可．【分析】根据已知等式，【解答】解：（a﹣b）（a+b）=a2﹣b2；（a﹣b）（a2+ab+b2）=a3﹣b3；（a﹣b）（a3+a2b+ab2+b3）=a4﹣b4； …可得到（a﹣b）（a2016+a2015b+…+ab2015+b2016）=a2017﹣b2017 ，故答案：a2017﹣b2017 为　题题题三、解答（本大共8小，共66分） ﹣π）0．计19．算： +2sin60°+|3﹣ |﹣（实幂值【考点】数的运算；零指数；特殊角的三角函数．题简【分析】本涉及二次根式化、特殊角的三角函数值绝对值负幂整数指数 4个考点．、、计时针对别进每个考点分计实则算，然后根据数的运算法求得计结算果．在算，需要行【解答】解： +2sin60°+|3﹣ |﹣（ ﹣π）0 =3+2× +3﹣ ﹣1 =3+ +3﹣ ﹣1 =5．　组20．解方程：．组【考点】解二元一次方程．组【分析】方程利用加减消元法求出解即可． 12 【解答】解：，①×8+②得：33x=33，即x=1，把x=1代入①得：y=1，则组方程的解为．　顶21．△ABC的点坐标为标A（﹣2，3）、B（﹣3，1）、C（﹣1，2），以坐原点O 为转旋中顺时针转别旋 90°，得到△A′B′C′，点B′、C′分是点B、C的对应心，点．过（1）求点B′的反比例函数解析式；线（2）求段CC′的长．标图变转化-旋．【考点】待定系数法求反比例函数解析式；坐与形图转转转【分析】（1）据形旋方向以及旋中心和旋角度得出点，根据待定系数法，即对应可求出解．转转（2）根据勾股定理求得OC，然后根据旋的旋求得OC′，最后根据勾股定理即可求得．图图【解答】解：（1）如所示：由知B点的坐标为转转（﹣3，1），根据旋中心O，旋方向顺时针转，旋角度90°，对应标为（1，3），点B的设过点B′的坐为点B′的反比例函数解析式 y= ， ∴k=3×1=3，过为∴点B′的反比例函数解析式 y= ．（2）∵C（﹣1，2）， ∴OC= ∵△ABC以坐原点O =，标为转顺时针转旋 90°，旋中心， ∴OC′=OC= ∴CC′= 　，=．边22．已知平行四形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F． 13 证（1）求：△ABF≌△CDE；图（2）如，若∠1=65°，求∠B的大小．边质质【考点】平行四形的性；全等三角形的判定与性．边质【分析】（1）由平行四形的性得出AB=CD，AD∥BC，∠B=∠D，得出∠1=∠DCE，证结出果证∠AFB=∠1，由AAS 明△ABF≌△CDE即可；边质（2）由（1）得∠1=∠DCE=65°，由平行四形的性和三角形内角和定理即可得出．证边边【解答】（1）明：∵四形ABCD是平行四形， ∴AB=CD，AD∥BC，∠B=∠D， ∴∠1=∠DCE， ∵AF∥CE， ∴∠AFB=∠ECB， ∵CE平分∠BCD， ∴∠DCE=∠ECB， ∴∠AFB=∠1，在△ABF和△CDE中，，∴△ABF≌△CDE（AAS）；（2）解：由（1）得：∠1=∠ECB，∠DCE=∠ECB， ∴∠1=∠DCE=65°， ∴∠B=∠D=180°﹣2×65°=50°．　义23．某校在践行“社会主核心价值观讲赛对选中，名列前20名的手的合分数m 综进”演比组统计结果如表所示：行分，组组频数号分一6≤m＜7 7≤m＜8 8≤m＜9 9≤m≤10 2二7a2三四值（1）求a的；图对应图圆的（2）若用扇形来描述，求分数在8≤m＜9内所的扇形心角大小；选记为：A1、A2，在第四内的两名手组（3）将在第一内的两名选记为组手：B1、B2，从第组树组选和第四中随机取2名选进调谈组选选研座，求第一至少有1名手被中的概率（一用手行图结或列表法列出所有可能果）．状14 树图频统计图．【考点】列表法与【分析】（1）根基被（2）根据表格中的数据可以得到分数在8≤m＜9内所状法；数（率）分布表；扇形调查为值图人数 20和表格中的数据可以求得a的；的对应圆的扇形心角大；题组选（3）根据意可以写出所有的可能性，从而可以得到第一至少有1名手被中的概率选．题【解答】解：（1）由意可得， a=20﹣2﹣7﹣2=9，值即a的是9；题（2）由意可得，对应图圆为心角：360°× =36°；分数在8≤m＜9内所的扇形的题图（3）由意可得，所有的可能性如下所示，组选选故第一至少有1名手被中的概率是： = ，组选选即第一至少有1名手被中的概率是．　墙长 24．在直角角AOB（OA⊥OB，且OA、OB 度不限）中，要砌20m 长墙墙，与直角角AOB 围的2为成地面矩形的储仓积为，且地面矩形AOBC的面 96m ．这（1）求地面矩形的长；规为单（2）有格 0.80×0.80和1.00×1.00（位：m）的地板砖单别为块 55元/ 和80元/ 价分计缝规隙），用哪一种格的块选砖，若只其中一种地板都恰好能铺满储仓的矩形地面（不砖费较少？地板用应【考点】一元二次方程的用．题长【分析】（1）根据意表示出方形的长进长宽积而利用 × =面，求出即可；，15 别计规砖费较（2）分【解答】（1） x（20﹣x）=96，解得x1=12，x2=8（舍去），算出每一格的地板所需的用，然后比即可．设这长则题依意得：地面矩形的是xm，这长答：地面矩形的是12米；规为费（2）格 0.80×0.80所需的用：96×（0.80×0.80）×55=8250（元）．规为费格 1.00×1.00所需的用：96×（1.00×1.00）×80=7680（元）．为因 8250＜7680，规为所以采用格 1.00×1.00所需的费较用少．　图为为线25．如，已知AB ⊙O的直径，AC ⊙O的切，OC交⊙O于点D，BD的延交AC于点E．长线证（1）求：∠1=∠CAD；（2）若AE=EC=2，求⊙O的半径．线【考点】切的性质．为为线证【分析】（1）由AB ⊙O的直径，AC ⊙O的切，易得∠CAD=∠BDO，继证结论得；而证（2）由（1）易得△CAD∽△CDE，然后由相似三角形的对应边长成比例，求得CD的，再利用勾股定理，求得答案．证为【解答】（1）明：∵AB ⊙O的直径， ∴∠ADB=90°， ∴∠ADO+∠BDO=90°，为∵AC ⊙O的切线，∴OA⊥AC， ∴∠OAD+∠CAD=90°， ∵OA=OD， ∴∠OAD=∠ODA， ∵∠1=∠BDO， ∴∠1=∠CAD；（2）解：∵∠1=∠CAD，∠C=∠C， ∴△CAD∽△CDE， ∴CD：CA=CE：CD， ∴CD2=CA•CE， ∵AE=EC=2， ∴AC=AE+EC=4， ∴CD=2 ，16 设则为则 ⊙O的半径 x， OA=OD=x， 222Rt△AOC中，OA +AC =OC ， ∴x2+42=（2 +x）2，解得：x= ∴⊙O的半径　．为．边长为对线线经过相交于点P，抛物 L O、P、A三点，点E是正方形 26．正方形OABC的 4，角线动内的抛物上的点．（1）建立适当的平面直角坐系，标标①直接写出O、P、A三点坐；线②求抛物 L的解析式；积（2）求△OAE与△OCE面之和的最大值．综题．【考点】二次函数合为线【分析】（1）以O点原点，段OA所在的直线为轴 x线线为轴 y 建立直角，段OC所在的直标边长结质标合正方形的性即可得出点O、P、A三点的坐；② 抛物设坐系．①根据正方形的 2线为结标L的解析式 y=ax +bx+c，合点O、P、A的坐利用待定系数法即可求出抛物的解析线式；（2）由点E 正方形内的抛物上的点，出点E的坐为线动设标结积合三角形的面公式找出S ，质△OAE+SOCE关于m的函数解析式，根据二次函数的性即可得出结论．为线【解答】解：（1）以O点原点，段OA所在的直线为轴 x线线为轴段OC所在的直 y 建立，标图直角坐系，如所示．边长为对线角①∵正方形OABC的 4，相交于点P，标为标为标为（2，2）． ∴点O的坐（0，0），点A的坐 2（4，0），点P的坐设线为抛物 L的解析式 y=ax +bx+c， ②线经过 ∵抛物 L O、P、A三点， ∴有，17 解得：，线为∴抛物 L的解析式 y=﹣ （2）∵点E是正方形内的抛物上的点，标为 +2m）（0＜m＜4）， +2x．线动设∴点E的坐（m，﹣ ∴S△OAE+SOCE= OA•yE+ OC•xE=﹣m2+4m+2m=﹣（m﹣3）2+9，时积值为 ∴当m=3 ，△OAE与△OCE面之和最大，最大9．　18