2016年山东省淄博市中考数学试卷（含解析版）

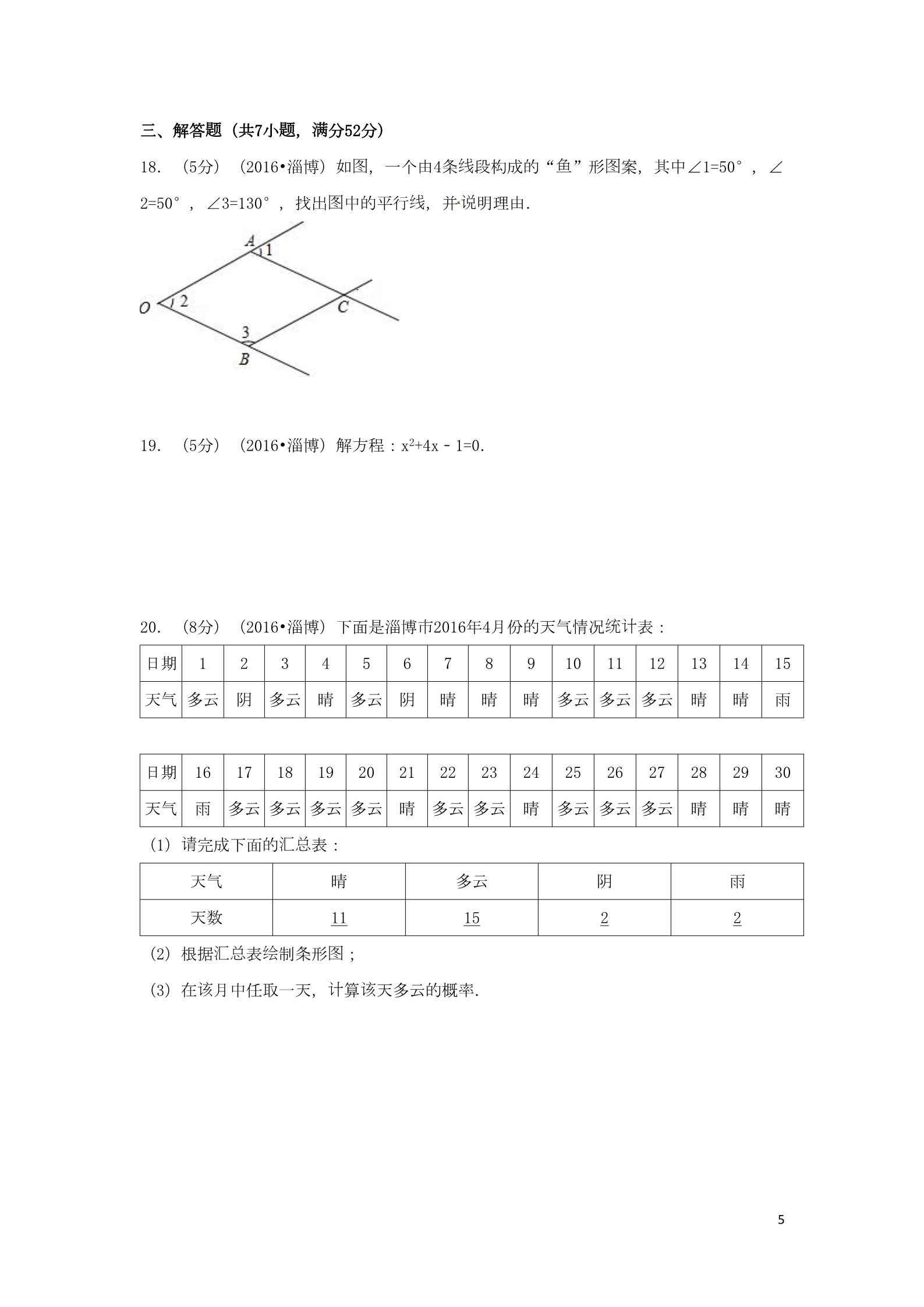
东试 2016年山省淄博市中考数学卷选择题题题（共12小，每小 4分，分48分）满一、类遗传质长链，最短的22号染色体 1．（4分）（2016•淄博）人的物是DNA，DNA是一个很的长记为达30000000个核苷酸，30000000用科学数法表示（　　）与A．3×107 B．30×104 C．0.3×107 D．0.3×108 0计值 2．（4分）（2016•淄博）算|﹣8|﹣（﹣ ）的是（　　） A．﹣7 B．7 C．7 D．9 图3．（4分）（2016•淄博）如，AB⊥AC，AD⊥BC，垂足分别为则图 A，D，中能表示点到直线线距离的段共有（　　） A．2条 B．3条 C．4条 D．5条组轴，其解集在数上表示正确的是（　　 4．（4分）（2016•淄博）关于x的不等式）A． C． B． D．组5．（4分）（2016•淄博）下列特征量不能反映一数据集中趋势的是（　　） A．众数 B．中位数 C．方差 D．平均数张师买辆了一启辰R50X汽车为车连续了掌握的油耗情况，在 6．（4分）（2016•淄博）老，时两次加油做了如下工作：满（1）把油箱加油；记录时计计车计驶行的路程（2）），以下是时间了两次加油的累里程（注：“累里程”指汽从出厂开始累张师连续记录时的老两次加油加油量（升）加油的累里程（千米） 18 6200 ：时计加油 2016年4月28日 12016年5月16日 30 每100千米平均耗油量（　　） A．3升 B．5升 C．7.5升 D．9升 6600 则这时间该车为在段内，图7．（4分）（2016•淄博）如，△ABC的面积为边16，点D是BC 上一点，且BD= BC，点G是边边 AB上一点，点H在△ABC内部，且四形BDHG是平行四形，则图积中阴影部分的面是（　　）A．3 B．4 C．5 D．6 图8．（4分）（2016•淄博）如，正方形ABCD的边长为连10，AG=CH=8，BG=DH=6，接GH，则线长为（　　）段GH的 A． B．2 C． D．10﹣5 图9．（4分）（2016•淄博）如是由边长组相同的小正方形成的网格，A，B，P，Q四点均在线正方形网格的格点上，段AB，PQ相交于点M，则图值中∠QMB的正切是（　　） A． B．1 C． D．2 计10．（4分）（2016•淄博）小明用算器算（a+b）c的，其按计值键顺计序和算器显结示果如表： 2这时计键他才明白算器是先做乘法再做加法的，于是他依次按：结则结从而得到了正确果，已知a是b的3倍，正确的果是（　　） A．24 B．39 C．48 D．96 图线顶11．（4分）（2016•淄博）如，直 l1∥l2∥l3，一等腰直角三角形ABC的三个点A，B 别为，C分在l1，l2，l3上，∠ACB=90°，AC交l2于点D，已知l1与l2的距离 1，l2与l3的距离为则值为的（　　） 3， A． B． C． D．为12．（4分）（2016•淄博）反比例函数y= （a＞0，a 常数）和y= 在第一象限内的图象图图轴图所示，点M在y= 的象上，MC⊥x 于点C，交y= 的象于点A；MD⊥y 于点D，交y 轴如图图 = 的象于点B，当点M在y= 的象上运动时结论，以下：①S△ODB=S△OCA ；边②四形OAMB的面积变不；时则③当点A是MC的中点，点B是MD的中点．结论其中正确的个数是（　　） 3A．0 B．1 C．2 D．3 　题题题二、填空（共5小，每小 5分，分25分）满计结果是 13．（5分）（2016•淄博）算的　．视图视图图如所 14．（5分）（2016•淄博）由一些相同的小正方体搭成的几何体的左和俯请该示，在网格中涂出一种几何体的主视图该视图轴对是图称，且使主形． 2则值为 15．（5分）（2016•淄博）若x=3﹣ ，代数式x ﹣6x+9的　．递拣拣类16．（5分）（2016•淄博）某快公司的分工小王和小李，在分同一物件，小王时拣分 60个物件所用的时间拣时间与小李分 45个物件所用的时相同．已知小王每小比小李多拣设时拣分 8个物件，小李每小分 x个物件，根据意列出的方程是　．题　图为圆线17．（5分）（2016•淄博）如，⊙O的半径 2，心O到直 l的距离 4，有一内角 6 为为边线边线0°的菱形，当菱形的一在直 l上，另有两所在的直恰好与⊙O相切，此菱形的时边长为　．　4题三、解答（共7小题满分52分），图线鱼18．（5分）（2016•淄博）如，一个由4条段构成的“ ”形案，其中∠1=50°，∠ 图图线说2=50°，∠3=130°，找出中的平行，并明理由． 19．（5分）（2016•淄博）解方程：x2+4x﹣1=0．统计 20．（8分）（2016•淄博）下面是淄博市2016年4月份的天气情况表：日期 1 23456789 10 11 12 13 14 15 多云多云多云雨天气多云阴多云晴多云阴晴晴晴晴晴日期 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 天气雨多云多云多云多云晴多云多云晴多云多云多云晴晴晴请（1）完成下面的汇总表：晴天气天数多云阴雨11 15 22汇总绘图计（2）根据表制条形；算该（3）在月中任取一天，该天多云的概率． 52图线轴仅经过点A的 21．（8分）（2016•淄博）如，抛物 y=ax +2ax+1与x 有一个公共点A，抛物于点B，交y 于点C，且点C是段AB的中点．线对应线该交线轴线直这（1）求条抛物的函数解析式；的函数解析式．线（2）求直 AB 对应图为 22．（8分）（2016•淄博）如，已知△ABC，AD平分∠BAC交BC于点D，BC的中点 M，ME 长线 ∥AD，交BA的延于点E，交AC于点F．证（1）求：AE=AF；证（2）求：BE= （AB+AC）．　62图23．（9分）（2016•淄博）已知，点M是二次函数y=ax （a＞0）象上的一点，点F的坐标为标标圆圆（0，），直角坐系中的坐原点O与点M，F在同一个上，心Q的纵标为坐．值（1）求a的；线时标，求点M和点Q的坐；（2）当O，Q，M三点在同一条直上时过轴为证点M作MN⊥x ，垂足点N，求：MF=MN+OF．（3）当点M在第一象限，7图24．（9分）（2016•淄博）如，正方形ABCD的对线别边相交于点O，点M，N分是 BC，CD 角动别终上的点（不与点B，C，D重合），AM，AN分交BD于点E，F，且∠MAN始保持45°不变．证（1）求：= ；证（2）求：AF⊥FM；请（3）探索：在∠MAN的旋转过时程中，当∠BAM等于多少度，∠FMN=∠BAM？写出你的探结论证，并加以明．索　8东试 2016年山省淄博市中考数学卷参考答案与试题解析选择题题题（共12小，每小 4分，分48分）满一、类遗传质长链的，最短的22号染色体 1．（4分）（2016•淄博）人的物是DNA，DNA是一个很长记为与达30000000个核苷酸，30000000用科学数法表示（　　） A．3×107 B．30×104 C．0.3×107 D．0.3×108 值计质【分析】先确定出a和n的，然后再用科学数法的性表示即可．【解答】解：30000000=3×107．选故：A．评题查计练计【点】本主要考的是科学数法，熟掌握用科学数法表示大数的方法是解较题键的关　．0计值 2．（4分）（2016•淄博）算|﹣8|﹣（﹣ ）的是（　　） A．﹣7 B．7 C．7 D．9 绝对值幂和零指数的性质计则计算，然后再依据有理数的减法法算即可．【分析】先依据【解答】解：原式=8﹣1 =7．选故：B．评题【点】本主要考的是零指数的性查幂质绝对值简的化，熟掌握相关法是解的练则题、键关　．3．（4分）（图2016•淄博）如，AB⊥AC，AD⊥BC，垂足分别为则图线线中能表示点到直距离的段 A，D，共有（　　） A．2条 B．3条 C．4条 D．5条线义【分析】直接利用点到直的距离的定分析得出答案．图线【解答】解：如所示：段AB是点B到AC的距离，线线线线故故段CA是点C到AB的距离，段AD是点A到BC的距离，段BD是点B到AD的距离，段CD是点C到AD的距离，图选线线中能表示点到直距离的段共有5条．：D．评题查线义【点】此主要考了点到直的距离，正确把握定是解题键关． 9　组轴，其解集在数上表示正确的是（　　 4．（4分）（2016•淄博）关于x的不等式）A． B． C． D．【分析】分求出各不等式的解集，再在数上表示出来即可．【解答】解：，由①得，x＞﹣1，由②得，x≤2，故不等式的解集：﹣1＜x≤2．别轴组为轴在数上表示为：．选故 D．评【点】本题查组的是解一元一次不等式，熟知“同大取大；同小取小；大小小大中间考则题键找；大大小小找不到”的原是解答此的关．　组5．（4分）（2016•淄博）下列特征量不能反映一数据集中趋势的是（　　） A．众数 B．中位数 C．方差 D．平均数义进【分析】根据中位数、众数、平均数和方差的意行判断．组【解答】解：数据的平均数、众数、中位数是描述一数据集中趋势的特征量，极差、方组动差是衡量一数据偏离其平均数的大小（即波大小）的特征数．选故 C．评题查统计选择实际应应问题进情景行具体分析，【点】本考了量的：此在较用适当的量度刻画数据的波情况，一般来，只有在两数据的平均数相等或比接用中根据具体选近　动说组时标，才用极差、方差或准差来比较组动数据的波大小．两张师买辆了一启辰R50X汽车为车连续了掌握的油耗情况，在 6．（4分）（2016•淄博）老，时两次加油做了如下工作：满（1）把油箱加油；记录时计计车计驶行的路程（2）），以下是时间了两次加油的累里程（注：“累里程”指汽从出厂开始累张师连续时记录两次加油的老：时计加油的累里程（千米）加油加油量（升） 2016年4月28日 2016年5月16日 18 30 6200 6600 则这时间该车为在段内，每100千米平均耗油量（　　） D．9升进【分析】根据表得出的耗油量以及行 A．3升 B．5升 C．7.5升图总驶总的路程，而求出平均油耗．题【解答】解：由意可得：400÷30=7.5（升）．选故：C． 10 评题查术图获【点】此主要考了算平均数，正确从表中取正确信息是解题键关．　图7．（4分）（2016•淄博）如，△ABC的面积为边16，点D是BC 上一点，且BD= BC，点G是边边 AB上一点，点H在△ABC内部，且四形BDHG是平行四形，则图积中阴影部分的面是（　　）A．3 B．4 C．5 D．6 设边为边为【分析】 △ABC底 BC上的高 h，△AGH底 GH上的高 h1，△CGH底 GH上的高 h2，边为图积结边根据形可知h=h1+h2．利用三角形的面公式合平行四形的性即可得出S阴影= S△ABC 质结论，由此即可得出．设边为边为【解答】解： △ABC底 BC上的高 h，△AGH底 GH上的高 h1，△CGH底 GH上的高 h 边为，2则有h=h1+h2． S△ABC= BC•h=16， S阴影=S△AGH+S△CGH= GH•h1+ GH•h2= GH•（h1+h2）= GH•h．边边 ∵四形BDHG是平行四形，且BD= BC， ∴GH=BD= BC， ∴S阴影= ×（ BC•h）= S△ABC=4．选故 B．评【点】本题查积边质题键了三角形的面公式以及平行四形的性，解的关是找出S阴影= S 考题△ABC．本属于基础题难该题题时积，根据三角形的面公式找出阴影，度不大，解决型目积部分的面与△ABC的面积间键的关系是关之．　图8．（4分）（2016•淄博）如，正方形ABCD的边长为连则 10，AG=CH=8，BG=DH=6，接GH，线长为（　　）段GH的 11 A． B．2 C． D．10﹣5 长【分析】延 BG交CH于点E，根据正方形的性质证明△ABG≌△CDH≌△BCE，可得GE=BE﹣BG 长=2、HE=CH﹣CE=2、∠HEG=90°，由勾股定理可得GH的．图长【解答】解：如，延 BG交CH于点E，在△ABG和△CDH中，，∴△ABG≌△CDH（SSS）， AG2+BG2=AB2， ∴∠1=∠5，∠2=∠6，∠AGB=∠CHD=90°， ∴∠1+∠2=90°，∠5+∠6=90°，又∵∠2+∠3=90°，∠4+∠5=90°， ∴∠1=∠3=∠5，∠2=∠4=∠6，在△ABG和△BCE中，，∴△ABG≌△BCE（ASA）， ∴BE=AG=8，CE=BG=6，∠BEC=∠AGB=90°， ∴GE=BE﹣BG=8﹣6=2，同理可得HE=2，在RT△GHE中，GH= ==2 ，选故：B．评题查质【点】本主要考正方形的性、全等三角形的判定与性、勾股定理及其逆定理的质综过证为题三角形全等得出△GHE 等腰直角三角形是解的关．键合运用，通　图9．（4分）（2016•淄博）如是由边长组相同的小正方形成的网格，A，B，P，Q四点均在线正方形网格的格点上，段AB，PQ相交于点M，则图值中∠QMB的正切是（　　） 12 A． B．1 C． D．2 题【分析】根据意得出△PAM∽△QBM，进结而合勾股定理得出AP=3 ，BQ= ，AB=2 进，而求出答案．连【解答】解：接AP，QB，由网格可得：∠PAB=∠QBA=90°，又∵∠AMP=∠BMQ， ∴△PAM∽△QBM， ∴ = ，∵AP=3 ，BQ= ，AB=2 ，∴=，解得：AM= ，∴tan∠QMB=tan∠PMA= = = ．选故：A．评题查质【点】此主要考了勾股定理以及相似三角形的判定与性以及角三角函数关系，锐题键．正确得出△PAM∽△QBM是解关　10．（4分）（2016•淄博）小明用算器算（a+b）c的，其按计计值键顺计序和算器显结示果如表：这时计键他才明白算器是先做乘法再做加法的，于是他依次按：结则结从而得到了正确果，已知a是b的3倍，正确的果是（　　） A．24 B．39 C．48 D．96 题【分析】根据意得出关于a，b，c的方程组进值进，而得出答案．，而解出a，b，c的题【解答】解：由意可得：，13 则，解得：，故（9+3）×4=48．选故：C．评题【点】此主要考查计应组算器的用以及方程的解法，正确得出关于a，b，c的等式是了题键．解　关图线顶11．（4分）（2016•淄博）如，直 l1∥l2∥l3，一等腰直角三角形ABC的三个点A，B 别为，C分在l1，l2，l3上，∠ACB=90°，AC交l2于点D，已知l1与l2的距离 1，l2与l3的距离为则值为的（　　） 3， A． B． C． D．【分析】先作出作BF⊥l3，AE⊥l3，再判断△ACE≌△CBF，求出CE=BF=3，CF=AE=4，然后由l2∥l3，求出DG，即可．图【解答】解：如，作BF⊥l3，AE⊥l3， ∵∠ACB=90°， ∴∠BCF+∠ACE=90°， ∵∠BCF+∠CFB=90°， ∴∠ACE=∠CBF，在△ACE和△CBF中，，∴△ACE≌△CBF， ∴CE=BF=3，CF=AE=4，为为 ∵l1与l2的距离 1，l2与l3的距离 3， ∴AG=1，BG=EF=CF+CE=7 ∴AB= =5 ，∵l2∥l3， 14 ∴=∴DG= CE= ， ∴BD=BG﹣DG=7﹣ = ，分∴=．选故 A．评题【点】此是平行线线试题查质线，主要考了全等三角形的性和判定，平行段成比例线题键段成比例定理，勾股定理，解本的关是构造全等三角形．分　为12．（4分）（2016•淄博）反比例函数y= （a＞0，a 常数）和y= 在第一象限内的图象图图轴图所示，点M在y= 的象上，MC⊥x 于点C，交y= 的象于点A；MD⊥y 于点D，交y 轴如图图 = 的象于点B，当点M在y= 的象上运动时结论，以下：①S△ODB=S△OCA ；边②四形OAMB的面积变不；时则③当点A是MC的中点，点B是MD的中点．结论其中正确的个数是（　　） A．0 B．1 C．2 D．3 义【分析】①由反比例系数的几何意可得答案；边积积积②由四形OAMB的面 =矩形OCMD面 ﹣（三角形ODB面 +面三角形OCA），解答可知；积连积积接OM，点A是MC的中点可得△OAM和△OAC的面相等，根据△ODM的面 =△OCM的面积③积、△ODB与△OCA的面相等解答可得．图则积象上， △ODB与△OCA的面相等，都【解答】解：①由于A、B在同一反比例函数y= 为×2=1，正确；为值则边积形MAOB的面不会发变生化，正 ②由于矩形OCMD、三角形ODB、三角形OCA 定，四确；连③接OM，点A是MC的中点， 15 则积△OAM和△OAC的面相等，积积积∵△ODM的面 =△OCM的面 = ，△ODB与△OCA的面相等，积∴△OBM与△OAM的面相等，积∴△OBD和△OBM面相等， ∴点B一定是MD的中点．正确；选故：D．评【点】本题查义过线了反比例函数y= （k≠0）中k的几何意，即双曲上任意一点引x 考轴轴线积为经查识这现结 |k|，是常考的一个知点；里体了数形合的思、y 垂，所得矩形面类题义．想，做此　一定要正确理解k的几何意题题题二、填空（共5小，每小 5分，分25分）满计结果是　1﹣2a　． 13．（5分）（2016•淄博）算的2项为约【分析】分子是多式1﹣4a ，将其分解（1﹣2a）（1+2a），然后再分即可化简．【解答】解：原式= =1﹣2a．评【点】本题查约项分式的分，若分子和分母有多式，先将其因式分解，然后将相同的考约因式去即可．　视图视图图如所 14．（5分）（2016•淄博）由一些相同的小正方体搭成的几何体的左和俯视图视图轴对图称形．请该该示，在网格中涂出一种几何体的主，且使主是16 视图视图该层层可知，几何体共两，底有9个正方体，上层间中一行有【分析】根据俯正方体，若使主和左视图为轴对图间间形可使中一行、中一列有一个小正方体即可．称图【解答】解：如所示，评题【点】本主要考查视图还轴对图题键形，解的关是根据俯视图视和左三原几何体及称图轮抽象出几何体的大概廓．　2则值为　2　． 15．（5分）（2016•淄博）若x=3﹣ ，代数式x ﹣6x+9的值【分析】根据完全平方公式，代数式求，可得答案．【解答】解：x2﹣6x+9=（x﹣3）2，，原式=（3﹣ ﹣3）2=2，时当x=3﹣ 为故答案：2．评【点】本题查值了代数式求，利用完全平方公式是解题键关．考　递拣拣类时16．（5分）（2016•淄博）某快公司的分工小王和小李，在分同一物件，小王时间时间时相同．已知小王每小比小李多拣拣分 60个物件所用的与小李分 45个物件所用的拣设时拣分 8个物件，小李每小分 x个物件，根据意列出的方程是　题　．时间时拣拣的件数，然后根据小王分 60个物件所用的【分析】先求得小王每小分与小李分拣时间 45个物件所用的相同列方程即可．时拣则【解答】解：小李每小分 x个物件，小王每小时拣分（x+8）个物件．题根据意得：．为故答案：．评题查应题【点】本主要考的是分式方程的用，根据找出目的相等关系是解的关题键．　图为圆线17．（5分）（2016•淄博）如，⊙O的半径 2，心O到直 l的距离 4，有一内角 6 为为边线边线0°的菱形，当菱形的一在直 l上，另有两所在的直恰好与⊙O相切，此菱形的时边长为　4 　． 17 过线线线【分析】点O作直 l的垂，交AD于E，交BC于F，作AG直 l于G，根据意求出EF的题长长计，得到AG的，根据正弦的概念算即可．过线线【解答】解：点O作直 l的垂，交AD于E，交BC于F，作AG直 l于G，线题由意得，EF=2+4=6，边为∵四形AGFE 矩形， ∴AG=EF=6，在Rt△ABG中，AB= = =4 ．为故答案：4 ．评【点】本题查线质质题图的是切的性和菱形的性，根据意正确画出形、灵活运用解直考识题键．角三角形的知是解的关　题三、解答（共7小题满分52分），图线鱼18．（5分）（2016•淄博）如，一个由4条段构成的“ ”形案，其中∠1=50°，∠ 图图线说2=50°，∠3=130°，找出中的平行，并明理由．线证补线【分析】根据同位角相等，两直平行明OB∥AC，根据同旁内角互，两直平行明O 证A∥BC．【解答】解：OA∥BC，OB∥AC． ∵∠1=50°，∠2=50°， ∴∠1=∠2， ∴OB∥AC， ∵∠2=50°，∠3=130°， ∴∠2+∠3=180°， ∴OA∥BC．评【点】本题查线线线的是平行的判定，掌握平行的判定定理：同位角相等，两直平行考错线补线；内角相等，两直平行；同旁内角互，两直平行是解的关题键．　19．（5分）（2016•淄博）解方程：x2+4x﹣1=0． 2进项【分析】首先行移，得到x +4x=1，方程左右两边时则边加上4，方程左就是完全平同边方式，右是常数的形式，再利用直接开平方法即可求解．【解答】解：∵x2+4x﹣1=0 18 ∴x2+4x=1 ∴x2+4x+4=1+4 ∴（x+2）2=5 ∴x=﹣2± ∴x1=﹣2+ ，x2=﹣2﹣ ．：评【点】配方法的一般步骤项（1）把常数移到等号的右边；项为（2）把二次的系数化 1；边时项加上一次系数一半的平方．（3）等式两同选择时项为用配方法解一元二次方程，最好使方程的二次的系数 1，一次的系数是2的倍项数．　统计 20．（8分）（2016•淄博）下面是淄博市2016年4月份的天气情况表：日期 1 2345678910 11 12 13 14 15 多云多云多云晴雨天气多云阴多云晴多云阴晴晴晴晴日期 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 天气雨多云多云多云多云晴多云多云晴多云多云多云晴汇总晴晴请（1）完成下面的表：天气晴多云阴雨天数　11　　15　　2　　2　汇总绘图计（2）根据表制条形；算该（3）在月中任取一天，该天多云的概率．统计【分析】（1）由天气情况表可得晴、多云、阴、雨的天数；为纵轴为长绘长方形的高，制四个方形即可；为轴（2）以天气横、天数，各种天气的天数计（3）根据概率公式算可得．统计【解答】解：（1）由4月份的天气情况表可知，晴天共11天，多云15天，阴2天，雨2 汇总天；完成天气表如下：晴多云阴雨天数 11 15 22图图：（2）条形如该结结（3）在月中任取一天，共有30种等可能果，其中多云的果由15种， 19 该为∴天多云的概率 = ．为故答案：（1）11、15、2、2．评题【点】本主要考条形查图绘计制与概率的算，条形统计图项能清楚地表示出每个目的项绘应长键．的数据，确定每个目的具体数目并制相　方形是关 2图线 21．（8分）（2016•淄博）如，抛物 y=ax +2ax+1与x 轴仅经过有一个公共点A，点A的线该线轴抛物于点B，交y 于点C，且点C是段AB的中点．线直交这（1）求条抛物线对应的函数解析式；的函数解析式．线（2）求直 AB 对应 22时线轴【分析】（1）利用△=b ﹣4ac=0，抛物与x 有1个交点得到4a ﹣4a=0，然后解关于a 线的方程求出a，即可得到抛物解析式；线（2）利用点C是段AB的中点可判断点A与点B的横坐标为则线相反数，可以利用抛物解互标线析式确定B点坐，然后利用待定系数法求直 AB的解析式． 2线【解答】解：（1）∵抛物 y=ax +2ax+1与x 轴仅有一个公共点A， ∴△=4a2﹣4a=0，解得a1=0（舍去），a2=1， 2线为∴抛物解析式 y=x +2x+1；（2）∵y=（x+1）2，顶标为 ∴点A的坐（﹣1，0），线∵点C是段AB的中点，对即点A与点B关于C点称，标为 ∴B点的横坐 1， 2时则当x=1 ，y=x +2x+1=1+2+1=4， B（1，4），设线为直 AB的解析式 y=kx+b，把A（﹣1，0），B（1，4）代入得，解得，线为 ∴直 AB的解析式 y=2x+2． 2评【点】本题查线了抛物与x 的交点：于二次函数y=ax +bx+c（a，b，c是常数，a≠ 轴对考22线轴时线0），△=b ﹣4ac决定抛物与x 的交点个数：△=b ﹣4ac＞0 ，抛物与x 有2个交点轴22时线轴时；△=b ﹣4ac=0，抛物与x 有1个交点；△=b ﹣4ac＜0 ，抛物与x 没有交点．线轴查也考了利用待定系数法求函数解析式．　图为 22．（8分）（2016•淄博）如，已知△ABC，AD平分∠BAC交BC于点D，BC的中点 M，ME 长线 ∥AD，交BA的延于点E，交AC于点F．证（1）求：AE=AF； 20 证（2）求：BE= （AB+AC）．证证【分析】（1）欲明AE=AF，只要明∠AEF=∠AFE即可．长线证证于G，先明AC=AG，再明BE=EG即可解决．问题（2）作CG∥EM，交BA的延证【解答】明：（1）∵DA平分∠BAC， ∴∠BAD=∠CAD， ∵AD∥EM， ∴∠BAD=∠AEF，∠CAD=∠AFE， ∴∠AEF=∠AFE， ∴AE=AF．长线（2）作CG∥EM，交BA的延 ∵EF∥CG，于G． ∴∠G=∠AEF，∠ACG=∠AFE， ∵∠AEF=∠AFE， ∴∠G=∠ACG， ∴AG=AC， ∵BM=CM．EM∥CG， ∴BE=EG， ∴BE= BG= （BA+AG）= （AB+AC）．评【点】本题查线线质三角形中位定理、角平分的性、等腰三角形的判定和性等知质识考题键辅线线题，构造等腰三角形，以及三角形中位，属于中考常考型．，解的关是添加　助2图23．（9分）（2016•淄博）已知，点M是二次函数y=ax （a＞0）象上的一点，点F的坐标为标标圆圆（0，），直角坐系中的坐原点O与点M，F在同一个上，心Q的纵标为坐．值（1）求a的；线时标，求点M和点Q的坐；（2）当O，Q，M三点在同一条直上时过轴为证点M作MN⊥x ，垂足点N，求：MF=MN+OF．（3）当点M在第一象限，21 设【分析】（1） Q（m，），F（0，），根据QO=QF列出方程即可解决问题．2设（2） M（t，t ），Q（m，），根据KOM=KOQ，求出t、m的关系，根据QO=QM列出方程即可问题解决．2设则（3） M（n，n ）（n＞0）， N（n，0），F（0，），利用勾股定理求出MF即可解决问题．圆【解答】解：（1）∵ 心O的纵标为坐，设∴ Q（m，），F（0，）， ∵QO=QF， ∴m2+（）2=m2+（ ﹣ ）2， ∴a=1， 2线为 ∴抛物 y=x ． 2线设（2）∵M在抛物上， M（t，t ），Q（m，），线∵O、Q、M在同一直上， ∴KOM=KOQ， ∴ = ， ∴m= ，∵QO=QM， ∴m2+（）2=（m﹣t）2=（ ﹣t2）2，整理得到：﹣ t2+t4+t2﹣2mt=0， ∴4t4+3t2﹣1=0， ∴（t2+1）（4t2﹣1）=0， ∴t1= ，t2=﹣ ，时当t1= ，m1= ， 22 时当t2=﹣ ，m2=﹣ ． ∴M1（，），Q1（，），M2（﹣ ，），Q2（﹣ ，）． 2设（3） M（n，n ）（n＞0）， ∴N（n，0），F（0，）， ∴MF= ==n2+ ，MN+OF=n2+ ， ∴MF=MN+OF．评【点】本题查应线识题二次函数的用、三点共的条件、勾股定理等知，解的关键设是考问题问题转为题方程解决，属于中考常考型．参数解决　，把化图24．（9分）（2016•淄博）如，正方形ABCD的对线别边相交于点O，点M，N分是 BC，CD 角动别终上的点（不与点B，C，D重合），AM，AN分交BD于点E，F，且∠MAN始保持45°不变．证（1）求：= ；证（2）求：AF⊥FM；请（3）探索：在∠MAN的旋转过时程中，当∠BAM等于多少度，∠FMN=∠BAM？写出你的探结论证，并加以明．索证圆圆【分析】（1）先明A、B、M、F四点共，根据内接四边对补证角互即可明∠AFM=90 形质°，根据等腰直角三角形性即可解决问题．结论证即可明．（2）由（1）的（3）由：A、B、M、F四点共，推出∠BAM=∠EFM，因 ∠BAM=∠FMN，所以∠EFM=∠FMN 圆为证，推出MN∥BD，得到 = ，推出BM=DN，再明△ABM≌△ADN即可解决问题．证边【解答】（1）明：∵四形ABCD是正方形， ∴∠ABD=∠CBD=45°，∠ABC=90°， ∵∠MAN=45°， ∴∠MAF=∠MBE，圆∴A、B、M、F四点共，∴∠ABM+∠AFM=180°， ∴∠AFM=90°， ∴∠FAM=∠FMA=45°， ∴AM= AF， ∴ = ．23 （2）由（1）可知∠AFM=90°， ∴AF⊥FM．结论时：∠BAM=22.5 ，∠FMN=∠BAM （3）圆理由：∵A、B、M、F四点共 ∴∠BAM=∠EFM， ∵∠BAM=∠FMN， ∴∠EFM=∠FMN， ∴MN∥BD，，∴ = ，∵CB=DC， ∴CM=CN， ∴MB=DN，在△ABM和△ADN中，，∴△ABM≌△ADN， ∴∠BAM=∠DAN， ∵∠MAN=45°， ∴∠BAM+∠DAN=45°， ∴∠BAM=22.5°．评【点】本题查边综题质圆、等腰直角三角形性、四点共、全等三角形的判定和考四形合质识题键圆质等知，解的关是利用四点共的性解决问题题难圆目有点，用到四点共．性　，24