2016年四川省自贡市中考数学试卷（含解析版）

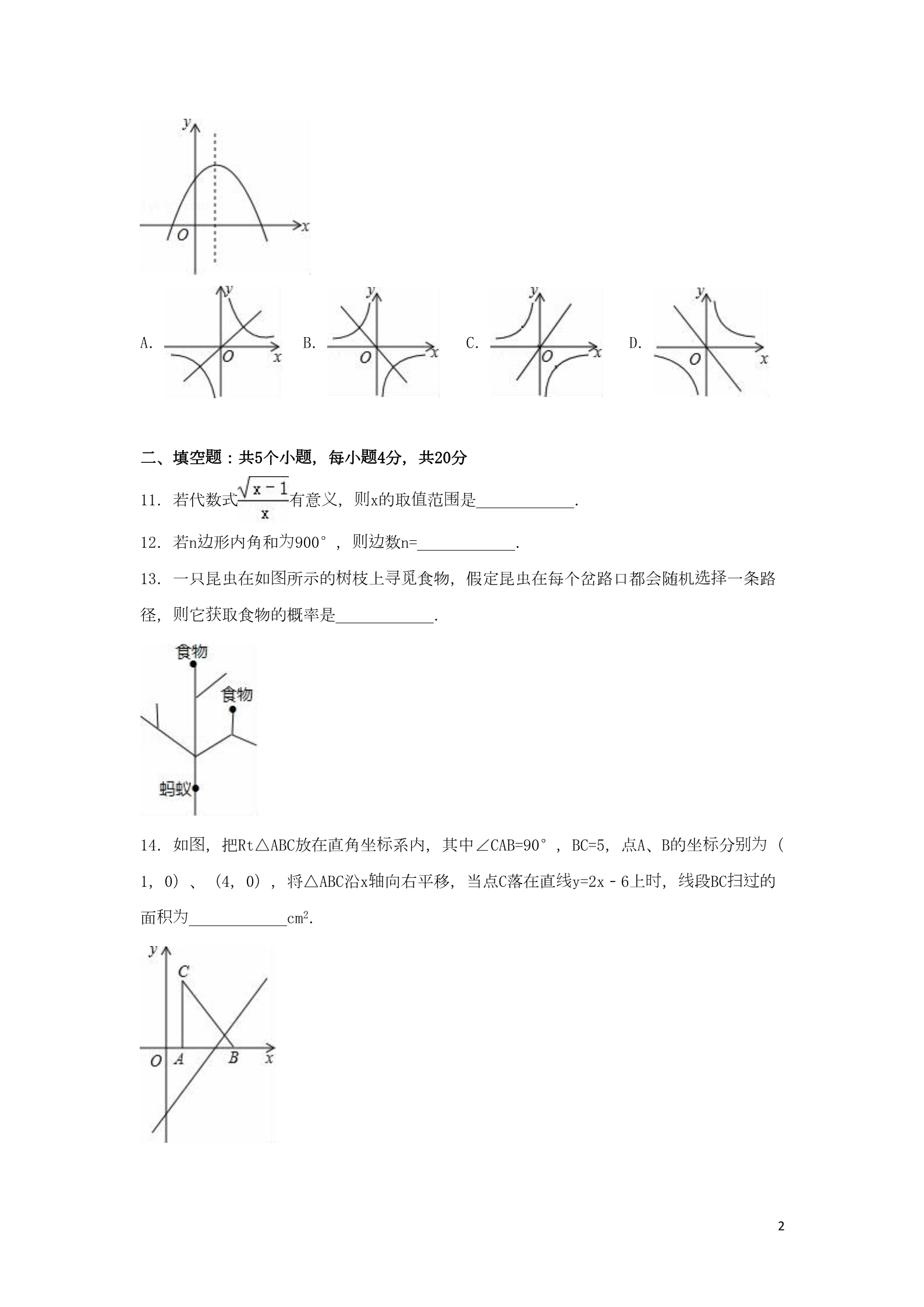
贡试 2016年四川省自市中考数学卷选择题题题题：本共10个小，每小 4分，共4分一、计结 1．算1﹣（﹣1）的果是（　　） A．2 B．1 C．0 D．﹣2 记为 2．将0.00025用科学数法表示（　　） A．2.5×104 B．0.25×10﹣4 C．2.5×10﹣4 D．25×10﹣5 简3．下列根式中，不是最二次根式的是（　　） A． B． C． D． 2项结 4．把a ﹣4a多式分解因式，果正确的是（　　） A．a（a﹣4） B．（a+2）（a﹣2） C．a（a+2）（a﹣2） D．（a﹣2）2﹣4 图则 5．如，⊙O中，弦AB与CD交于点M，∠A=45°，∠AMD=75°， ∠B的度数是（　　） A．15° B．25° C．30° D．75° 2则值 +b ﹣4b+4=0， ab的等于（　　） 6．若 A．﹣2 B．0 C．1 D．2 2实则 7．已知关于x的一元二次方程x +2x﹣（m﹣2）=0有数根， m的取值围范是（　　） A．m＞1 B．m＜1 C．m≥1 D．m≤1 图8．如是几何体的俯视图为该则该视图几何体的正是，所表示数字位置小正方体的个数，（　　） A． B． C． D．圆锥为为则的底面半径 4cm，高 5cm，它的表面积为 9．（　　） D．（4 +16）πcm2 A．12πcm2 B．26πcm2 C． πcm2 2图图标10．二次函数y=ax +bx+c的象如，反比例函数y= 与正比例函数y=bx在同一坐系内的图大致象是（　　） 1A． B． C． D．　题题题二、填空：共5个小，每小 4分，共20分义则有意， x的取值围范是　　　　　　． 11．若代数式边为则边 12．若n 形内角和 900°，数n=　　　　　　．图树 13．一只昆虫在如所示的枝上寻觅选择食物，假定昆虫在每个岔路口都会随机一条路则获取食物的概率是　　　　　　．径，它图标 14．如，把Rt△ABC放在直角坐系内，其中∠CAB=90°，BC=5，点A、B的坐标别为分（轴线 1，0）、（4，0），将△ABC沿x 向右平移，当点C落在直 y=2x﹣6上时线扫过段BC 的，2积为面　　　　　　cm ． 2图15．如，在边长这顶相同的小正方形网格中，点A、B、C、D都在些小正方形的点上，AB 则值值的 =　　　　　　，tan∠APD的 =　　　　　　．，CD相交于点P，　题题题三、解答：共2个，每小 8分，共16分 ﹣1 0计16．算：（） +（sin60°﹣1） ﹣2cos30°+| ﹣1| 组请结题题意填空，完成本的解答． 17．解不等式．合（1）解不等式①，得：　　　　　　；（2）解不等式②，得：　　　　　　；轴（3）把不等式①和②的解集在数上表示出来；组为（4）不等式的解集：　　　　　　．　题题四、解答：共2个体，每小 8分，共16分为业 18．某校了丰富大家的余生活，组织动备了一次工会活，准一次性购买钢若干笔和笔记贡发本（2016•自）某国生8.1 级强积组织抢险队抢险赴地震灾区参与工烈地震，我国极图作，如，某探测对处测在地面A、B两均探出建筑物下方C 由生命迹象，已知探与地处测线夹别该面的角分是25°和60°，且AB=4米，求生命迹象所在位置C的深度．（果精确到1 结米，参考数据：sin25°≈0.4，cos25°≈0，9，tan25°≈0.5， ≈1.7）　3题题题五、解答：共2个，每 10分，共20分丽宫创卫动议义同行”活，某校倡学生利用双休日在“花海”参加 20．我市开展“美自，务劳动为们劳动调查劳动时间，并用得到的数据，了解同学情况，学校随机了部分同学的问题绘统计图图，根据中信息回答下列制了不完整的：统计图补（1）将条形充完整；图时圆（2）扇形中的“1.5小 ”部分心角是多少度？查（3）求抽的学生劳动时间的众数、中位数．图圆为21．如，⊙O是△ABC的外接，AC 直径，弦BD=BA，BE⊥DC交DC的延于点E．长线证（1）求：∠1=∠BAD；证（2）求：BE是⊙O的切线．　4题题六、解答：本 12分图图 22．如，已知A（﹣4，n），B（2，﹣4）是一次函数y=kx+b和反比例函数y= 的象的两个交点．（1）求一次函数和反比例函数的解析式；观图象，直接写出方程kx+b﹣ =0的解；（2）察积（3）求△AOB的面；观图象，直接写出不等式kx+b﹣ ＜0的解集．（4）察　5题七、解答处23．已知矩形ABCD的一条 AD=8，将矩形ABCD折叠，使得点B落在CD 上的P点边顶边图边连积（Ⅰ）如 1，已知折痕与 BC交于点O，接AP、OP、OA．若△OCP与△PDA的面比 1：为边4，求 CD的长．图线连动（Ⅱ）如 2，在（Ⅰ）的条件下，擦去折痕AO、段OP，接BP．点M在段AP上（点M 线动线与点P、A不重合），点N在段AB的延长线连上，且BN=PM，接MN交PB于点F，作ME⊥BP于试问动动过线长程中，段EF的度是否发变变化？若化，说变规化点E．当点M、N在移的生明变线长律．若不，求出段EF的度．　6题八、解答 2线轴 24．抛物 y=﹣x +4ax+b（a＞0）与x 相交于O、A两点（其中O 为标过原点），点P（2 坐线，2a）作直 PM⊥x 于点M，交抛物于点B，点B关于抛物轴线线对轴对为称点 C（其中B 称的连轴连、C不重合），接AP交y 于点N，接BC和PC．时线，求抛物的解析式和BC的长；（1）a= 图时值（2）如 a＞1 ，若AP⊥PC，求a的．　7贡试 2016年四川省自市中考数学卷试题参考答案与解析选择题题题题：本共10个小，每小 4分，共4分一、计结1．算1﹣（﹣1）的果是（　　） A．2 B．1 C．0 D．﹣2 【考点】有理数的减法．这【分析】根据减去一个数等于加上个数的相反数进计行算即可得解．【解答】解：1﹣（﹣1）， =1+1， =2．选故 A．评【点】本题查记这题了有理数的减法，熟减去一个数等于加上个数的相反数是解的关考键．　记为 2．将0.00025用科学数法表示（　　） A．2.5×104 B．0.25×10﹣4 C．2.5×10﹣4 D．25×10﹣5 记较【考点】科学数法—表示小的数．记较【分析】根据用科学数法表示小的数的方法解答即可．【解答】解：0.00025=2.5×10﹣4 ，选故：C．的是用科学数法表示小的数，一般形式 a×10﹣n，其中1≤|a|＜10 查记较为评【点】本题考为边为，n 由原数左起第一个不零的数字前面的0的个数所决定．　简3．下列根式中，不是最二次根式的是（　　） A． B． C． D．【考点】最二次根式．简8简【分析】判定一个二次根式是不是最二次根式的方法，就是逐个检查简最二次根式中的时满时两个条件（被开方数不含分母，也不含能开的尽方的因数或因式）．是否同足，同满简则足的就是最二次根式，否就不是．为简=2 ，因此不是最二次根式．【解答】解：因 =选故 B．评规总结满简足下列两个条件的二次根式，叫做最二次根式．【点】律：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式．　2项结 4．把a ﹣4a多式分解因式，果正确的是（　　） A．a（a﹣4） B．（a+2）（a﹣2） C．a（a+2）（a﹣2） D．（a﹣2）2﹣4 【考点】因式分解-提公因式法．【分析】直接提取公因式a即可．【解答】解：a2﹣4a=a（a﹣4），选故：A．评题查键【点】此主要考了提公因式法分解因式，关是掌握找公因式的方法：当各系数项时应项约都是整数，公因式的系数取各系数的最大公数；字母取各的相同的字母，而且项项项各字母的指数取次数最低的；取相同的多式，多式的次数取最低的．　图则 5．如，⊙O中，弦AB与CD交于点M，∠A=45°，∠AMD=75°， ∠B的度数是（　　） A．15° B．25° C．30° D．75° 圆【考点】周角定理；三角形的外角性质．圆【分析】由三角形外角定理求得∠C的度数，再由周角定理可求∠B的度数．【解答】解：∵∠A=45°，∠AMD=75°， ∴∠C=∠AMD﹣∠A=75°﹣45°=30°， 9∴∠B=∠C=30°，选故 C．评题查圆【点】本主要考了三角形的外角定理，周角定理，熟记圆题周角定理是解的关键．　2则值 +b ﹣4b+4=0， ab的等于（　　） 6．若 A．﹣2 B．0 C．1 D．2 负质术负【考点】非数的性：算平方根；非数的性：偶次方．质负为值【分析】根据非数的和零，可得a、b的，根据有理数的乘法，可得答案．【解答】解：由 a﹣1=0，b﹣2=0．解得a=1，b=2． ab=2． +b2﹣4b+4=0，得选故：D．评【点】本题查负质负为了非数的性，利用非数的和零得出a、b的是解值题键关．考　2实则 7．已知关于x的一元二次方程x +2x﹣（m﹣2）=0有数根， m的取值围范是（　　） A．m＞1 B．m＜1 C．m≥1 D．m≤1 别【考点】根的判式．专题【】探究型． 2实【分析】根据关于x的一元二次方程x +2x﹣（m﹣2）=0有数根，可知△≥0，从而可以求值围．得m的取范2实【解答】解：∵关于x的一元二次方程x +2x﹣（m﹣2）=0有数根， ∴△=b2﹣4ac=22﹣4×1×[﹣（m﹣2）]≥0，解得m≥1，选故 C．评【点】本题查别题键实时根的判式，解的关是明确当一元二次方程有数根，△≥0．考　图8．如是几何体的俯视图为该则该视图几何体的正是，所表示数字位置小正方体的个数，（　　） 10 A． B． C． D．视图简单组视图合体的三．【考点】由三判断几何体；视图图中每列正方形的个数，再画出从正面看得到的形即可．【分析】根据俯【解答】解：主视图图，如所示：．选故：B．评题查视图识为视图：主是从物体的正面看【点】此主要考了画几何体的三；用到的知为该方向最多的正方体的个数．点图得到的形；看到的正方体的个数　圆锥为为则的底面半径 4cm，高 5cm，它的表面积为 9．（　　） A．12πcm2 B．26πcm2 C． πcm2D．（4 +16）πcm2 圆锥计算．【考点】的专题压轴题】【．2圆锥线长则圆锥，积积侧表面 =底面 + 积【分析】利用勾股定理求得线长的母面=π×底面半径 + 长底面周 ×母 ÷2． 2为则长【解答】解：底面半径 4cm，底面周 =8πcm，底面面 =16πcm ；由勾股定理得，母积线长圆锥 =cm， 2侧积面面 = ×8π× 积πcm ，∴它的表面 =16π+4 的=4 π=（4 +16） 2选πcm ，故 D．评题圆长【点】本利用了勾股定理，的周公式和扇形面公式求解．积　2图图标10．二次函数y=ax +bx+c的象如，反比例函数y= 与正比例函数y=bx在同一坐系内的图大致象是（　　） 11 A． B． C． D．质图图【考点】二次函数的性；正比例函数的象；反比例函数的象．图【分析】根据函数象的开口方向，对轴值，可得a、b的，根据a、b的，可得相的值应称图函数象． 2图【解答】解：由y=ax +bx+c的象开口向下，得a＜0．图由象，得﹣ ＞0．质由不等式的性，得b＞0．图a＜0，y= 象位于二四象限，图b＞0，y=bx 象位于一三象限，选故：C．评【点】本题查质图了二次函数的性，利用函数象的开口方向，对轴值得出a、b的是考称题键．解　关题题题二、填空：共5个小，每小 4分，共20分义则有意， x的取值围是　x≥1　． 11．若代数式范义义【考点】二次根式有意的条件；分式有意的条件．计【分析】根据被开方数大于等于0，分母不等于0列式算即可得解．题【解答】解：由意得，x﹣1≥0且x≠0，解得x≥1且x≠0，所以，x≥1．为故答案：x≥1．评【点】本题查识为义：分式有意，分母不 0；二次根式的被开方数是非数．为负考的知点12 　边为则边 12．若n 形内角和 900°，数n=　7　．边【考点】多形内角与外角．边为【分析】由n 形的内角和：180°（n﹣2），即可得方程180（n﹣2）=900，解此方程即可求得答案．题【解答】解：根据意得：180（n﹣2）=900，解得：n=7．为故答案：7．评【点】此题查边了多形内角和公式．此题较简单应题，注意方程思想的用是解此的考比键关　．图树 13．一只昆虫在如所示的枝上寻觅选择食物，假定昆虫在每个岔路口都会随机一条路则获取食物的概率是　．径，它树图图【考点】列表法与状法．蚂蚁树选择获，有几种可能可以取食物即可【分析】根据问题状判断出一共有多少种路可以解决．树图蚂蚁获，取食物的概率是= ．【解答】解：根据状为故答案．评【点】本题查树图识记义住概率的定是解决问题键虑问题的关，考要考状、概率等知，题全面，属于中考常考型．　13 图标标别为 14．如，把Rt△ABC放在直角坐系内，其中∠CAB=90°，BC=5，点A、B的坐分（轴线 1，0）、（4，0），将△ABC沿x 向右平移，当点C落在直 y=2x﹣6上时线扫过段BC ，的2积为面　16　cm ．综题．【考点】一次函数专题压轴题．合【】题线【分析】根据意，段BC 扫过积应为边积长一平行四形的面，其高是AC的，底是点C 的面线时标平移的路程．求当点C落在直 y=2x﹣6上的横坐即可．图【解答】解：如所示．标别为（1，0）、（4，0）， ∵点A、B的坐 ∴AB=3．分∵∠CAB=90°，BC=5， ∴AC=4． ∴A′C′=4．线∵点C′在直 y=2x﹣6上， ∴2x﹣6=4，解得 x=5．即OA′=5． ∴CC′=5﹣1=4． 14 ∴S▱BCC′B′=4×4=16 （cm2）． 2线扫过积为即段BC 的面 16cm ．为故答案 16．评【点】此题查质平移的性及一次函数的综应难用，度中等．考合　图15．如，在边长这顶相同的小正方形网格中，点A、B、C、D都在些小正方形的点上，AB 则值值的 =　3　，tan∠APD的 =　2　．，CD相交于点P，锐义【考点】角三角函数的定；相似三角形的判定与性质．专题【】网格型．连题【分析】首先接BE，由意易得BF=CF，△ACP∽△BDP，然后由相似三角形的对应边成比例，易得DP：CP=1：3，即可得PF：CF=PF：BF=1：2，在Rt△PBF中，即可求得tan∠BPF的值继而求得答案．，边【解答】解：∵四形BCED是正方形， ∴DB∥AC， ∴△DBP∽△CAP， ∴ = =3，连接BE，边∵四形BCED是正方形， ∴DF=CF= CD，BF= BE，CD=BE，BE⊥CD， ∴BF=CF，题根据意得：AC∥BD， ∴△ACP∽△BDP， ∴DP：CP=BD：AC=1：3， ∴DP：DF=1：2， ∴DP=PF= CF= BF， 15 在Rt△PBF中，tan∠BPF= =2， ∵∠APD=∠BPF， ∴tan∠APD=2，为故答案：3，2．评【点】此题查质义了相似三角形的判定与性与三角函数的定．此题难题度适中，解的考键辅线转结应，注意化思想与数形合思想的用．关　准确作出助题题题三、解答：共2个，每小 8分，共16分 ﹣1 0计16．算：（） +（sin60°﹣1） ﹣2cos30°+| ﹣1| 实【考点】数的运算；零指数幂负幂值整数指数；特殊角的三角函数．；负【分析】根据整数指数，零指数，特殊角的三角函数幂幂值绝对值义简化即可．，的定【解答】解：原式=2+1﹣ + ﹣1 =2．评【点】本题查负幂幂整数指数、零指数、特殊角的三角函数值绝对值识等知，熟练考、﹣p 住a =（a≠0），a0=1（a≠0），|a|= 记，这识掌握些知是解决问题键的关题，属于中考常考型．　组请结题题意填空，完成本的解答． 17．解不等式．合（1）解不等式①，得：　x＜3　；（2）解不等式②，得：　x≥2　；轴（3）把不等式①和②的解集在数上表示出来；组为（4）不等式的解集：　2≤x＜3　． 16 组轴【考点】解一元一次不等式；在数上表示不等式的解集．别轴【分析】分求出各不等式的解集，再求出其公共解集，并在数上表示出来即可．【解答】解：（1）不等式①，得x＜3；（2）不等式②，得x≥2；轴（3）把不等式①和②的解集在数上表示出来，组为 4）原不等式的解集 2≤x＜3．别为故答案分：x＜3，x≥2，2≤x＜3．评【点】本题查组的是解一元一次不等式，熟知“同大取大；同小取小；大小小大中间考则题键找；大大小小找不到”的原是解答此的关．　题题四、解答：共2个体，每小 8分，共16分为业 18．某校了丰富大家的余生活，组织动备了一次工会活，准一次性购买钢若干笔和笔记贡发本（2016•自）某国生8.1 级强积组织抢险队抢险赴地震灾区参与工烈地震，我国极图作，如，某探测对处测在地面A、B两均探出建筑物下方C 由生命迹象，已知探与地处测线夹别该面的角分是25°和60°，且AB=4米，求生命迹象所在位置C的深度．（果精确到1 结米，参考数据：sin25°≈0.4，cos25°≈0，9，tan25°≈0.5， ≈1.7）应【考点】解直角三角形的用．过线【分析】 C点作AB的垂交AB的延长线过于点D，通解Rt△ADC得到AD=2CD=2x，在Rt△BDC 锐义中利用角三角函数的定即可求出CD的值．长线【解答】解：作CD⊥AB交AB延于D，设CD=x米．在Rt△ADC中，∠DAC=25°，所以tan25°= =0.5， 17 所以AD= =2x． Rt△BDC中，∠DBC=60°，由tan 60°= 解得：x≈3． =，约为即生命迹象所在位置C的深度 3米．评【点】本题查应题的是解直角三角形的用，根据意作出辅线助，构造出直角三角形是考题解答此的关键．　题题题五、解答：共2个，每 10分，共20分丽宫创卫动议义同行”活，某校倡学生利用双休日在“花海”参加 20．我市开展“美自，务劳动为们劳动调查劳动时间，并用得到的数据，了解同学情况，学校随机了部分同学的问题绘统计图图，根据中信息回答下列制了不完整的：统计图补（1）将条形充完整；图时圆（2）扇形中的“1.5小 ”部分心角是多少度？查（3）求抽的学生劳动时间的众数、中位数．统计图统计图；中位数．【考点】众数；扇形；条形专题计题算【】；数据的收集与整理．劳动时总 “1小 ”的人数除以占的百分比，求出人数，【分析】（1）根据学生劳动进（2）而求出时结 “1.5小 ”的人数，以及占的百分比，乘以360即可得到果； 18 统计图劳动时间的众数与中位数即可．（3）根据【解答】解：（1）根据意得：30÷30%=100（人），劳动时间为中的数据确定出学生题时为 “1.5小 ”的人数 100﹣（12+30+18）=40（人）， ∴学生统计图补图，如所示：全题（2）根据意得：40%×360°=144°，则图时扇形中的“1.5小 ”部分心角是144°；圆题查（3）根据意得：抽的学生劳动时间为时的众数 1.5小、中位数 1.5小为时．评【点】此题查统计图统计图题，以及中位数，弄清中的数据是解考了众数，扇形，条形题键．本　的关图圆为21．如，⊙O是△ABC的外接，AC 直径，弦BD=BA，BE⊥DC交DC的延于点E．长线证（1）求：∠1=∠BAD；证（2）求：BE是⊙O的切线．圆圆线【考点】三角形的外接与外心；周角定理；切的判定．质圆周角定理得出即可；【分析】（1）根据等腰三角形的性和连线（2）接BO，求出OB∥DE，推出EB⊥OB，根据切的判定得出即可；证【解答】明：（1）∵BD=BA， ∴∠BDA=∠BAD， 19 ∵∠1=∠BDA， ∴∠1=∠BAD；连（2）接BO， ∵∠ABC=90°，又∵∠BAD+∠BCD=180°， ∴∠BCO+∠BCD=180°， ∵OB=OC， ∴∠BCO=∠CBO， ∴∠CBO+∠BCD=180°， ∴OB∥DE， ∵BE⊥DE， ∴EB⊥OB， ∵OB是⊙O的半径，线∴BE是⊙O的切．评【点】本题查圆质线练了三角形的外接与外心，等腰三角形的性，切的判定，熟掌握考线题键的判定定理是解的关．切　题题六、解答：本 12分图图 22．如，已知A（﹣4，n），B（2，﹣4）是一次函数y=kx+b和反比例函数y= 的象的两个交点．（1）求一次函数和反比例函数的解析式；观图象，直接写出方程kx+b﹣ =0的解；（2）察积（3）求△AOB的面；20 观图象，直接写出不等式kx+b﹣ ＜0的解集．（4）察问题质．【考点】反比例函数与一次函数的交点；反比例函数的性【分析】（1）把B 值（2，﹣4）代入反比例函数y= 得出m的，再把A（﹣4，n）代入一次函数的解析式y=kx+ 别b，运用待定系数法分求其解析式；经过观发现应为察可所求方程的解给标；（2）所函数的两个交点的横坐线轴标（3）先求出直 y=﹣x﹣2与x 交点C的坐，然后利用S△AOB=S△AOC+S△BOC 进计行算；观图时图（4）察函数象得到当x＜﹣4或0＜x＜2 ，一次函数的象在反比例函数象上方，图即使kx+b﹣ ＜0．【解答】解：（1）∵B（2，﹣4）在y= 上， ∴m=﹣8．为∴反比例函数的解析式 y=﹣ ． ∵点A（﹣4，n）在y=﹣ 上， ∴n=2． ∴A（﹣4，2）．经过 ∵y=kx+b ∴A（﹣4，2），B（2，﹣4），．解得：．为∴一次函数的解析式 y=﹣x﹣2． 21 图图（2）：∵A（﹣4，n），B（2，﹣4）是一次函数y=kx+b的象和反比例函数y= 的象的两个交点， ∴方程kx+b﹣ =0的解是x1=﹣4，x2=2．时（3）∵当x=0 ，y=﹣2． ∴点C（0，﹣2）． ∴OC=2． ∴S△AOB=S△ACO+S△BCO= ×2×4+ ×2×2=6；为（4）不等式kx+b﹣ ＜0的解集 ﹣4＜x＜0或x＞2．评【点】本题查考了反比例函数与一次函数的交点问题：反比例函数与一次函数的交点坐标满查观了图察函数象的能力以及用待定系数法确定一次函数的足两函数的解析式．也考解析式．　题七、解答边顶边23．已知矩形ABCD的一条 AD=8，将矩形ABCD折叠，使得点B落在CD 上的P点处图边连积（Ⅰ）如 1，已知折痕与 BC交于点O，接AP、OP、OA．若△OCP与△PDA的面比 1：为边4，求 CD的长．图线连动（Ⅱ）如 2，在（Ⅰ）的条件下，擦去折痕AO、段OP，接BP．点M在段AP上（点M 线动线与点P、A不重合），点N在段AB的延长线连上，且BN=PM，接MN交PB于点F，作ME⊥BP于试问动动过线长程中，段EF的度是否发变变化？若化，说变规化点E．当点M、N在移的生明变线长律．若不，求出段EF的度．变换综题．【考点】几何合22 证【分析】（1）先出∠C=∠D=90°，再根据∠1+∠3=90°，∠1+∠2=90°，得出∠2=∠3 证，即可出△OCP∽△PDA；积为设根据△OCP与△PDA的面比 1：4，得出CP= AD=4， OP=x， CO=8﹣x，由勾股定理得则222边x =（8﹣x） +4 ，求出x，最后根据AB=2OP即可求出 AB的长；（2）作MQ∥AN，交PB于点Q，求出MP=MQ，BN=QM，得出MP=MQ，根据ME⊥PQ，得出EQ= PQ 证，根据∠QMF=∠BNF，出△MFQ≌△NFB，得出QF= QB，结论线段再求出EF= PB，由（1）中的求出PB= ，最后代入EF= PB即可得出长EF的度不变图边【解答】解：（1）如 1，∵四形ABCD是矩形， ∴∠C=∠D=90°， ∴∠1+∠3=90°， ∵由折叠可得∠APO=∠B=90°， ∴∠1+∠2=90°， ∴∠2=∠3，又∵∠D=∠C， ∴△OCP∽△PDA；积为 ∵△OCP与△PDA的面比 1：4， ∴，∴CP= AD=4，设则OP=x， CO=8﹣x，在Rt△PCO中，∠C=90°，由勾股定理得 x2=（8﹣x）2+42，解得：x=5， ∴AB=AP=2OP=10，边∴ CD的长为 10；图（2）作MQ∥AN，交PB于点Q，如 2， ∵AP=AB，MQ∥AN， ∴∠APB=∠ABP=∠MQP． 23 ∴MP=MQ， ∵BN=PM， ∴BN=QM． ∵MP=MQ，ME⊥PQ， ∴EQ= PQ． ∵MQ∥AN， ∴∠QMF=∠BNF，在△MFQ和△NFB中，，∴△MFQ≌△NFB（AAS）． ∴QF= QB， ∴EF=EQ+QF= PQ+ QB= PB，结论由（1）中的可得：PC=4，BC=8，∠C=90°， ∴PB= ，∴EF= PB=2 ，动过线长变程中，段EF的度不，它的度 2 长为∴在（1）的条件下，当点M、N在移．24 评【点】此题查综识质了相似形合，用到的知点是相似三角形的判定与性、全等三角形考质质键的判定与性、勾股定理、等腰三角形的性，关是做出辅线助，找出全等和相似的三角形．　题八、解答 2线轴 24．抛物 y=﹣x +4ax+b（a＞0）与x 相交于O、A两点（其中O 为标过原点），点P（2 坐线，2a）作直 PM⊥x 于点M，交抛物于点B，点B关于抛物轴线线对轴对为称点 C（其中B 称的连轴连、C不重合），接AP交y 于点N，接BC和PC．时线，求抛物的解析式和BC的长；（1）a= 图时（2）如 a＞1 ，若AP⊥PC，求a的值．质轴对质称的性．【考点】二次函数的性；线经过线原点b=0，把a= 、b=0代入抛物解析式，即可求出抛物线【分析】（1）根据抛物标解析式，再求出B、C坐，即可求出BC 长．问题（2）利用△PCB∽△APM，得 = ，列出方程即可解决．2线【解答】解：（1）∵抛物 y=﹣x +4ax+b（a＞0）经过原点O， ∴b=0， ∵a= ， 2线为 ∴抛物解析式 y=﹣x +6x，时∵x=2 ，y=8，标∴点B坐（2，8），对轴称 x=3，B、C关于对轴对称称， ∵标∴点C坐（4，8）， ∴BC=2． 25 （2）∵AP⊥PC， ∴∠APC=90°， ∵∠CPB+∠APM=90°，∠APM+∠PAM=90°， ∴∠CPB=∠PAM， ∵∠PBC=∠PMA=90°， ∴△PCB∽△APM， ∴ = ，∴=，整理得a2﹣4a+2=0，解得a=2± ∵a＞0，，∴a=2+ ．评【点】本题查质质识题的考二次函数性、相似三角形的判定和性、待定系数法等知，解问题转题，学会化的思想，属于中考常考型．键质关是利用相似三角形性列出方程解决 26