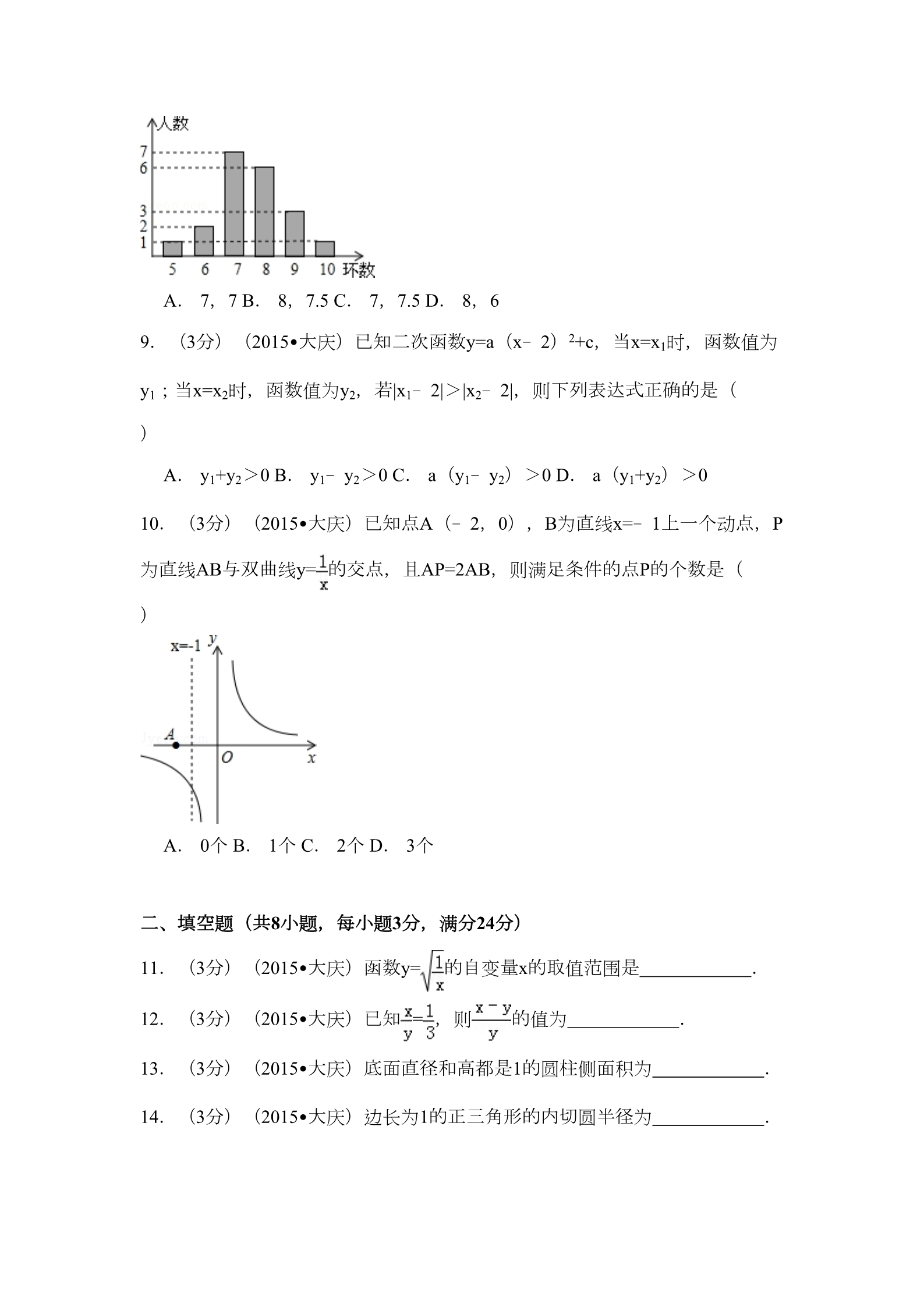
2015年黑龙江省大庆市中考数学试卷（含解析版）

2015年黑龙江省大庆市中考数学试卷一、选择题（共10小题，每小题3分，满分30分） 1．（3分）（2015•大庆）sin60°=（　　）　 A． B． C． 1 D． 2．（3分）（2015•大庆）将0.00007用科学记数法表示为（　　）　 A． 7×10﹣6 B． 70×10﹣5 C． 7×10﹣5 D． 0.7×10﹣6 3．（3分）（2015•大庆）a2的算术平方根一定是（　　）　 A． a B． |a| C． D． ﹣a 4．（3分）（2015•大庆）正n边形每个内角的大小都为108°，则n=（　　）　 A． 5 B． 6 C． 7 D． 8 5．（3分）（2015•大庆）某品牌自行车1月份销售量为100辆，每辆车售价相同．2月份的销售量比1月份增加10%，每辆车的售价比1月份降低了80元．2月份与1月份的销售总额相同，则1月份的售价为（　　）　 A． 880元 B． 800元 C． 720元 D． 1080元 6．（3分）（2015•大庆）在⊙O中，圆心O到弦AB的距离为AB长度的一半，则弦AB所对圆心角的大小为（　　）　 A． 30° B． 45° C． 60° D． 90° 7．（3分）（2015•大庆）以下图形中对称轴的数量小于3的是（　　）　 A． B． C． D． 8．（3分）（2015•大庆）某射击小组有20人，教练根据他们某次射击的数据绘制如图所示的统计图，则这组数据的众数和中位数分别是（　　）　 A． 7，7 B． 8，7.5 C． 7，7.5 D． 8，6 9．（3分）（2015•大庆）已知二次函数y=a（x﹣2）2+c，当x=x1时，函数值为 y1；当x=x2时，函数值为y2，若|x1﹣2|＞|x2﹣2|，则下列表达式正确的是（　　）　 A． y1+y2＞0 B． y1﹣y2＞0 C． a（y1﹣y2）＞0 D． a（y1+y2）＞0 10．（3分）（2015•大庆）已知点A（﹣2，0），B为直线x=﹣1上一个动点，P 为直线AB与双曲线y= 的交点，且AP=2AB，则满足条件的点P的个数是（　　）　 A． 0个 B． 1个 C． 2个 D． 3个　二、填空题（共8小题，每小题3分，满分24分） 11．（3分）（2015•大庆）函数y= 的自变量x的取值范围是　　　　　　． 12．（3分）（2015•大庆）已知 = ，则的值为　　　　　　． 13．（3分）（2015•大庆）底面直径和高都是1的圆柱侧面积为　　　　　　． 14．（3分）（2015•大庆）边长为1的正三角形的内切圆半径为　　　　　　． 15．（3分）（2015•大庆）用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱　　　　　　（写出所有正确结果的序号）． 16．（3分）（2015•大庆）方程3（x﹣5）2=2（x﹣5）的根是　　　　　　． 17．（3分）（2015•大庆）若a2n=5，b2n=16，则（ab）n=　　　　　　． 18．（3分）（2015•大庆）在Rt△ABC中，∠C=90°，AC=BC=1，将其放入平面直角坐标系，使A点与原点重合，AB在x轴上，△ABC沿x轴顺时针无滑动的滚动，点A再次落在x轴时停止滚动，则点A经过的路线与x轴围成图形的面积为　　　　　　．　三、解答题（共10小题，满分66分） 19．（4分）（2015•大庆）求值： +（）2+（﹣1）2015 ．20．（4分）（2015•大庆）解关于x的不等式：ax﹣x﹣2＞0．　21．（5分）（2015•大庆）已知实数a，b是方程x2﹣x﹣1=0的两根，求 + 的值．　22．（6分）（2015•大庆）已知一组数据x1，x2，…x6的平均数为1，方差为 222（1）求：x1 +x2 +…+x6 ；（2）若在这组数据中加入另一个数据x7，重新计算，平均数无变化，求这7个数据的方差（结果用分数表示）　23．（7分）（2015•大庆）某商场举行开业酬宾活动，设立了两个可以自由转动的转盘（如图所示，两个转盘均被等分），并规定：顾客购买满188元的商品，即可任选一个转盘转动一次，转盘停止后，指针所指区域内容即为优惠方式；若指针所指区域空白，则无优惠．已知小张在该商场消费300元（1）若他选择转动转盘1，则他能得到优惠的概率为多少？（2）选择转动转盘1和转盘2，哪种方式对于小张更合算，请通过计算加以说明．24．（7分）（2015•大庆）小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据： ≈1.732， ≈1.414．结果保留整数） 25．（7分）（2015•大庆）如图，△ABC中，∠ACB=90°，D、E分别是BC、BA 的中点，联结DE，F在DE延长线上，且AF=AE．（1）求证：四边形ACEF是平行四边形；（2）若四边形ACEF是菱形，求∠B的度数． 26．（8分）（2015•大庆）如图，一次函数y=kx+b的图象与反比例函数y=﹣ 的图象交于A（﹣1，m）、B（n，﹣1）两点（1）求一次函数的解析式；（2）求△AOB的面积．　27．（9分）（2015•大庆）如图，四边形ABCD内接于⊙O，AD∥BC，P为BD 上一点，∠APB=∠BAD．（1）证明：AB=CD；（2）证明：DP•BD=AD•BC；（2）证明：BD2=AB2+AD•BC．　28．（9分）（2015•大庆）已知二次函数y=x2+bx﹣4的图象与y轴的交点为C，与x轴正半轴的交点为A，且tan∠ACO= （1）求二次函数的解析式；（2）P为二次函数图象的顶点，Q为其对称轴上的一点，QC平分∠PQO，求Q点坐标；（3）是否存在实数x1、x2（x1＜x2），当x1≤x≤x2时，y的取值范围为 ≤y≤ 若存在，直接写在x1，x2的值；若不存在，说明理由．？　　2015年黑龙江省大庆市中考数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分） 1．（3分）（2015•大庆）sin60°=（　　）　 A． B． C． 1 D．考点：特殊角的三角函数值．专题：计算题．分析：原式利用特殊角的三角函数值解得即可得到结果．解答：解：sin60°= 故选D ，点评：此题考查了特殊角的三角函数值，牢记特殊角的三角函数值是解本题的关键．　2．（3分）（2015•大庆）将0.00007用科学记数法表示为（　　）　 A． 7×10﹣6 B． 70×10﹣5 C． 7×10﹣5 D． 0.7×10﹣6 考点：科学记数法—表示较小的数．分析：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．解答：解：0.00007=7×10﹣5．故选：C．点评：本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．　3．（3分）（2015•大庆）a2的算术平方根一定是（　　）　 A． a B． |a| C． D． ﹣a 考点：算术平方根．分析：根据算术平方根定义，即可解答．解答：解：故选：B．点评： =|a|．本题考查了对算术平方根定义的应用，能理解定义并应用定义进行计算是解此题的关键，难度不是很大．　4．（3分）（2015•大庆）正n边形每个内角的大小都为108°，则n=（　　）　 A． 5 B． 6 C． 7 D． 8 考点：多边形内角与外角．分析：利用正多边形的性质得出其外角，进而得出多边形的边数．解答：解：∵正n边形每个内角的大小都为108°， ∴每个外角为：72°，则n= =5．故选：A．点评：此题主要考查了多边形内角与外角，正确得出其外角度数是解题关键．　5．（3分）（2015•大庆）某品牌自行车1月份销售量为100辆，每辆车售价相同．2月份的销售量比1月份增加10%，每辆车的售价比1月份降低了80元．2月份与1月份的销售总额相同，则1月份的售价为（　　）　 A． 880元 B． 800元 C． 720元 D． 1080元考点：一元一次方程的应用．分析：设1月份每辆车售价为x元，则2月份每辆车的售价为（x﹣80）元，依据“2月份的销售量比1月份增加10%，每辆车的售价比1月份降低了80元．2月份与1月份的销售总额相同”列出方程并解答．解答：解：设1月份每辆车售价为x元，则2月份每辆车的售价为（x﹣80）元，依题意得 100x=（x﹣80）×100×（1+10%），解得x=880．即1月份每辆车售价为880元．故选：A．点评：本题考查了一元一次方程的应用．根据题意得到“2月份每辆车的售价”和“2月份是销售总量”是解题的突破口．　6．（3分）（2015•大庆）在⊙O中，圆心O到弦AB的距离为AB长度的一半，则弦AB所对圆心角的大小为（　　）　 A． 30° B． 45° C． 60° D． 90° 考点：垂径定理；等腰直角三角形．分析：利用等腰直角三角形的性质以及垂径定理得出∠BOC的度数进而求出．解答：解：如图所示：连接BO，AO， ∵圆心O到弦AB的距离为AB长度的一半， ∴DO=DB，DO⊥AB， ∴∠BOC=∠BOC=45°，则∠A=∠AOC=45°， ∴∠AOB=90°．故选：D．点评：此题主要考查了垂径定理以及等腰直角三角形的性质，得出∠BOC=∠BOC=45° 是解题关键．　7．（3分）（2015•大庆）以下图形中对称轴的数量小于3的是（　　）　 A． B． C． D．考点：轴对称图形．分析：根据对称轴的概念求解．解答：解：A、有4条对称轴； B、有6条对称轴； C、有4条对称轴； D、有2条对称轴．故选D．点评：本题考查了轴对称图形，解答本题的关键是掌握对称轴的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．　8．（3分）（2015•大庆）某射击小组有20人，教练根据他们某次射击的数据绘制如图所示的统计图，则这组数据的众数和中位数分别是（　　）　 A． 7，7 B． 8，7.5 C． 7，7.5 D． 8，6 考点：众数；条形统计图；中位数．分析：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，可得答案．解答：解：在这一组数据中7是出现次数最多的，故众数是7；排序后处于中间位置的那个数是7，8，那么由中位数的定义可知，这组数据的中位数是故选：C．点评： =7.5；本题为统计题，考查极差、众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数），叫做这组数据的中位数．如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．　9．（3分）（2015•大庆）已知二次函数y=a（x﹣2）2+c，当x=x1时，函数值为 y1；当x=x2时，函数值为y2，若|x1﹣2|＞|x2﹣2|，则下列表达式正确的是（　　）　 A． y1+y2＞0 B． y1﹣y2＞0 C． a（y1﹣y2）＞0 D． a（y1+y2）＞0 考点：二次函数图象上点的坐标特征．分析：分a＞0和a＜0两种情况根据二次函数的对称性确定出y1与y2的大小关系，然后对各选项分析判断即可得解．解答：解：①a＞0时，二次函数图象开口向上， ∵|x1﹣2|＞|x2﹣2|， ∴y1＞y2，无法确定y1+y2的正负情况， a（y1﹣y2）＞0， ②a＜0时，二次函数图象开口向下， ∵|x1﹣2|＞|x2﹣2|， ∴y1＜y2，无法确定y1+y2的正负情况， a（y1﹣y2）＞0，综上所述，表达式正确的是a（y1﹣y2）＞0．故选C．点评：本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的对称性，难点在于根据二次项系数a的正负情况分情况讨论．　10．（3分）（2015•大庆）已知点A（﹣2，0），B为直线x=﹣1上一个动点，P 为直线AB与双曲线y= 的交点，且AP=2AB，则满足条件的点P的个数是（　　）　 A． 0个 B． 1个 C． 2个 D． 3个考点：反比例函数与一次函数的交点问题．分析：如图，设P（m，），B（﹣1，n），直线x=﹣1与x轴交于C，有A（﹣2，0），得到OA=2，OC=1，AC=1，BC∥y轴，推出，于是得到这样的点P 不存在，点P4在AB之间，不满足AP=2AB，过P2作P2Q⊥x轴于Q，求得满足条件的点P（﹣4，﹣ ），于是得到满足条件的点P的个数是1，解答：解：如图，设P（m，），B（﹣1，n），直线x=﹣1与x轴交于C， ∵A（﹣2，0）， ∴OA=2，OC=1， ∴AC=1，BC∥y轴， ∴，∴P1，P3在y轴上，这样的点P不存在，点P4在AB之间，不满足AP=2AB，过P2作P2Q⊥x轴于Q， ∴P2Q∥B1C， ∴∴= ， = ， ∴m=﹣4， ∴P（﹣4，﹣ ）， ∴满足条件的点P的个数是1，故选B．点评：本题考查了一次函数与反比例函数的焦点问题，平行线分线段成比例，注意数形结合思想的应用．　二、填空题（共8小题，每小题3分，满分24分） 11．（3分）（2015•大庆）函数y= 的自变量x的取值范围是　x＞0　．考点：函数自变量的取值范围．分析：根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，就可以求解．解答：解：根据二次根式有意义，分式有意义得：x≥0且x≠0，解得：x＞0．故答案为：x＞0．点评：本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．　12．（3分）（2015•大庆）已知 = ，则的值为　﹣ 　．考点：比例的性质．分析：根据已知设x=k，y=3k，代入求出即可．解答：解：∵ = ， ∴设x=k，y=3k， ∴==﹣ ，故答案为：﹣ ．点评：本题考查了比例的性质的应用，能选择适当的方法求出结果是解此题的关键，难度不大．　13．（3分）（2015•大庆）底面直径和高都是1的圆柱侧面积为　π　．考点：圆柱的计算．分析：圆柱的侧面积=底面周长×高．解答：解：圆柱的底面周长=π×1=π．圆柱的侧面积=底面周长×高=π×1=π．故答案是：π．点评：本题考查了圆柱的计算，熟记公式即可解答该题．　14．（3分）（2015•大庆）边长为1的正三角形的内切圆半径为　．考点：三角形的内切圆与内心．分析：根据等边三角形的三线合一，可以构造一个由其内切圆的半径、外接圆的半径和半边组成的30°的直角三角形，利用锐角三角函数关系求出内切圆半径即可．解答：解：∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形，则∠OBD=30°，BD= ， ∴tan∠BOD= ∴内切圆半径OD= 故答案为： =，=．．点评：此题主要考查了三角形的内切圆，注意：根据等边三角形的三线合一，可以发现其内切圆的半径、外接圆的半径和半边正好组成了一个30°的直角三角形．　15．（3分）（2015•大庆）用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱　①③④　（写出所有正确结果的序号）．考点：截一个几何体．分析：当截面的角度和方向不同时，圆柱体的截面无论什么方向截取圆柱都不会截得三角形．解答：解：①正方体能截出三角形； ②圆柱不能截出三角形； ③圆锥沿着母线截几何体可以截出三角形； ④正三棱柱能截出三角形．故截面可能是三角形的有3个．故答案为：①③④．点评：本题考查几何体的截面，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．　16．（3分）（2015•大庆）方程3（x﹣5）2=2（x﹣5）的根是　x1=5，x2= 　．考点：解一元二次方程-因式分解法．专题：计算题．分析：方程移项变形后，利用因式分解法求出解即可．解答：解：方程变形得：3（x﹣5）2﹣2（x﹣5）=0，分解因式得：（x﹣5）[3（x﹣5）﹣2]=0，可得x﹣5=0或3x﹣17=0，解得：x1=5，x2= ．故答案为：x1=5，x2= 点评：此题考查了解一元二次方程﹣因式分解法，熟练掌握因式分解的方法是解本题的关键．　17．（3分）（2015•大庆）若a2n=5，b2n=16，则（ab）n=　　．考点：幂的乘方与积的乘方．分析：根据幂的乘方与即的乘方，即可解答．解答：解：∵a2n=5，b2n=16， ∴（an）2=5，（bn）2=16， ∴，∴，故答案为：点评：．本题考查了幂的乘方与即的乘方，解决本题的关键是注意公式的逆运用．　18．（3分）（2015•大庆）在Rt△ABC中，∠C=90°，AC=BC=1，将其放入平面直角坐标系，使A点与原点重合，AB在x轴上，△ABC沿x轴顺时针无滑动的滚动，点A再次落在x轴时停止滚动，则点A经过的路线与x轴围成图形的面积为　 π+ 　．考点：旋转的性质；扇形面积的计算．专题：规律型．分析：由勾股定理求出AB，由题意得出点A经过的路线与x轴围成的图形是一个圆心角为135°，半径为的扇形，加上△ABC，再加上圆心角是90°，半径是1的扇形；由扇形的面积和三角形的面积公式即可得出结果．解答：解：∵∠C=90°，AC=BC=1， ∴AB= =；根据题意得： △ABC绕点B顺时针旋转135°，BC落在x轴上；△ABC再绕点C 顺时针旋转90°，AC落在x轴上，停止滚动； ∴点A的运动轨迹是：先绕点B旋转135°，再绕点C旋转90°；如图所示： ∴点A经过的路线与x轴围成的图形是：一个圆心角为135°，半径为的扇形，加上△ABC，再加上圆心角是90°，半径是1的扇形； ∴点A经过的路线与x轴围成图形的面积 =+ ×1×1+ =π+ ；故答案为：π+ ．点评：本题考查了旋转的性质、扇形面积的计算公式；根据题意得出点A经过的路线与x轴围成的图形由三部分组成是解决问题的关键．　三、解答题（共10小题，满分66分） 19．（4分）（2015•大庆）求值： +（）2+（﹣1）2015 ．考点：实数的运算．专题：计算题．分析：原式第一项利用算术平方根定义计算，第二项利用乘方的意义化简，第三项利用乘方的意义化简，计算即可得到结果．解答：解：原式= + ﹣1=﹣ ．点评：此题考查了实数的运算，熟练掌握运算法则是解本题的关键．　20．（4分）（2015•大庆）解关于x的不等式：ax﹣x﹣2＞0．考点：解一元一次不等式．专题：分类讨论．分析：利用不等式的基本性质，把不等号左边的﹣2移到右边，再根据a﹣1的取值，即可求得原不等式的解集．解答：解：ax﹣x﹣2＞0．（a﹣1）x＞2，当a﹣1=0，则ax﹣x﹣2＞0为空集，当a﹣1＞0，则x＞当a﹣1＜0，则a＜，．点评：此题考查了解简单不等式的能力，掌握解不等式要依据不等式的基本性质：（1）不等式的两边同时加上或减去同一个数或整式不等号的方向不变；（2）不等式的两边同时乘以或除以同一个正数不等号的方向不变；（3）不等式的两边同时乘以或除以同一个负数不等号的方向改变．　21．（5分）（2015•大庆）已知实数a，b是方程x2﹣x﹣1=0的两根，求 + 的值．考点：根与系数的关系．分析：根据根与系数的关系得到a+b=1，ab=﹣1，再利用完全平方公式变形得到 + = =，然后利用整体代入的方法进行计算．解答：解：∵实数a，b是方程x2﹣x﹣1=0的两根， ∴a+b=1，ab=﹣1， ∴ + = 点评： ==﹣3．本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=﹣ ，x1x2= ．　22．（6分）（2015•大庆）已知一组数据x1，x2，…x6的平均数为1，方差为 222（1）求：x1 +x2 +…+x6 ；（2）若在这组数据中加入另一个数据x7，重新计算，平均数无变化，求这7个数据的方差（结果用分数表示）考点：方差；算术平均数．分析：（1）先由数据x1，x2，…x6的平均数为1，得出x1+x2+…+x6=1×6=6，再根据方差为，得到S2= [（x1﹣1）2+（x2﹣1）2+…+（x6﹣1）2]= ，利用完全平方公式 222求出（x1 +x2 +…+x6 ﹣2×6+6）= ，进而求解即可；（2）先由数据x1，x2，…x7的平均数为1，得出x1+x2+…+x7=1×7=7，而x1+x2+…+ x6=6，所以x7=1；再根据 [（x1﹣1）2+（x2﹣1）2+…+（x6﹣1）2]= ，得出（x1 ﹣1）2+（x2﹣1）2+…+（x6﹣1）2=10，然后根据方差的计算公式即可求出这7 个数据的方差．解答：解：（1）∵数据x1，x2，…x6的平均数为1， ∴x1+x2+…+x6=1×6=6，又∵方差为， ∴S2= [（x1﹣1）2+（x2﹣1）2+…+（x6﹣1）2] 222= [x1 +x2 +…+x6 ﹣2（x1+x2+…+x6）+6] 222= （x1 +x2 +…+x6 ﹣2×6+6） 222= （x1 +x2 +…+x6 ）﹣1= ， 222∴x1 +x2 +…+x6 =16；（2）∵数据x1，x2，…x7的平均数为1， ∴x1+x2+…+x7=1×7=7， ∵x1+x2+…+x6=6， ∴x7=1， ∵ [（x1﹣1）2+（x2﹣1）2+…+（x6﹣1）2]= ， ∴（x1﹣1）2+（x2﹣1）2+…+（x6﹣1）2=10， ∴S2= [（x1﹣1）2+（x2﹣1）2+…+（x7﹣1）2] = [10+（1﹣1）2] =．点评：本题考查了平均数与方差的意义．平均数是指在一组数据中所有数据之和再除以数据的个数．一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．计算公式是：s2= [（x1﹣ ）2+（x2﹣ ）2+…+（xn﹣ ）2]．　23．（7分）（2015•大庆）某商场举行开业酬宾活动，设立了两个可以自由转动的转盘（如图所示，两个转盘均被等分），并规定：顾客购买满188元的商品，即可任选一个转盘转动一次，转盘停止后，指针所指区域内容即为优惠方式；若指针所指区域空白，则无优惠．已知小张在该商场消费300元（1）若他选择转动转盘1，则他能得到优惠的概率为多少？（2）选择转动转盘1和转盘2，哪种方式对于小张更合算，请通过计算加以说明．考点：列表法与树状图法．分析：（1）根据转盘1，利用概率公式求得获得优惠的概率即可；（2）分别求得转动两个转盘所获得的优惠，然后比较即可得到结论．解答：解：（1）∵整个圆被分成了12个扇形，其中有6个扇形能享受折扣， ∴P（得到优惠）= =；（2）转盘1能获得的优惠为：转盘2能获得的优惠为：40× =20元，所以选择转动转盘1更优惠．点评： =25元，本题考查了几何概率，考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．用到的知识点为：概率=相应的面积与总面积之比．　24．（7分）（2015•大庆）小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据： ≈1.732， ≈1.414．结果保留整数）考点：解直角三角形的应用-仰角俯角问题．分析：延长AE交CD于点G，设CG=xm，在直角△CGE中利用x表示出EG，然后在直角 △ACG中，利用x表示出AG，根据AE=AG﹣EG即可列方程求得x的值，进而球儿CD的长．解答：解：延长AE交CD于点G．设CG=xm，在直角△CGE中，∠CEG=45°，则EG=CG=xm．在直角△ACG中，AG= ∵AG﹣EG=AE， =xm． ∴x﹣x=30，解得：x=15（ +1）≈15×2.732≈40.98（m）．则CD=40.98+1.5=42.48（m）．答：这栋建筑物CD的高度约为42m．点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．　25．（7分）（2015•大庆）如图，△ABC中，∠ACB=90°，D、E分别是BC、BA 的中点，联结DE，F在DE延长线上，且AF=AE．（1）求证：四边形ACEF是平行四边形；（2）若四边形ACEF是菱形，求∠B的度数．考点：菱形的性质；平行四边形的判定．分析：（1）根据直角三角形斜边上的中线等于斜边的一半可得CE=AE=BE，从而得到 AF=CE，再根据等腰三角形三线合一的性质可得∠1=∠2，根据等边对等角可得然后∠F=∠3，然后求出∠2=∠F，再根据同位角相等，两直线平行求出CE∥AF，然后利用一组对边平行且相等的四边形是菱形证明；（2）根据菱形的四条边都相等可得AC=CE，然后求出AC=CE=AE，从而得到△ AEC是等边三角形，再根据等边三角形的每一个角都是60°求出∠CAE=60°，然后根据直角三角形两锐角互余解答．解答：（1）证明：∵∠ACB=90°，E是BA的中点， ∴CE=AE=BE， ∵AF=AE， ∴AF=CE，在△BEC中，∵BE=CE且D是BC的中点， ∴ED是等腰△BEC底边上的中线， ∴ED也是等腰△BEC的顶角平分线， ∴∠1=∠2， ∵AF=AE， ∴∠F=∠3， ∵∠1=∠3， ∴∠2=∠F， ∴CE∥AF，又∵CE=AF， ∴四边形ACEF是平行四边形；（2）解：∵四边形ACEF是菱形， ∴AC=CE，由（1）知，AE=CE， ∴AC=CE=AE， ∴△AEC是等边三角形， ∴∠CAE=60°，在Rt△ABC中，∠B=90°﹣∠CAE=90°﹣60°=30°．点评：本题考查了菱形的性质，平行四边形的判定，等边三角形的判定与性质，直角三角形斜边上的中线等于斜边的一半，以及直角三角形两锐角互余的性质，熟记各性质与判定方法是解题的关键．　26．（8分）（2015•大庆）如图，一次函数y=kx+b的图象与反比例函数y=﹣ 的图象交于A（﹣1，m）、B（n，﹣1）两点（1）求一次函数的解析式；（2）求△AOB的面积．考点：反比例函数与一次函数的交点问题．专题：计算题．分析：（1）把A与B坐标代入反比例解析式求出m与n的值，确定出A与B坐标，代入一次函数解析式求出k与b的值，即可确定出一次函数解析式；（2）由A与B的坐标求出AB的长，利用点到直线的距离公式求出原点O到直线 AB的距离，即可求出三角形AOB面积．解答：解：（1）把A（﹣1，m），B（n，﹣1）代入反比例函数y=﹣ ，得：m=7，n =7，即A（﹣1，7），B（7，﹣1），把A与B坐标代入一次函数解析式得：，解得：k=﹣1，b=6，则一次函数解析式为y=﹣x+6；（2）∵A（﹣1，7），B（7，﹣1）， ∴AB= =8 ，∵点O到直线y=﹣x+6的距离d= =3 ∴S△AOB= AB•d=24．点评：，此题考查了反比例函数与一次函数的交点问题，涉及的知识有：待定系数法求一次函数解析式，两点间的距离公式，以及点到直线的距离公式，熟练掌握待定系数法是解本题第一问的关键．　27．（9分）（2015•大庆）如图，四边形ABCD内接于⊙O，AD∥BC，P为BD 上一点，∠APB=∠BAD．（1）证明：AB=CD；（2）证明：DP•BD=AD•BC；（2）证明：BD2=AB2+AD•BC．考点：相似三角形的判定与性质；圆周角定理．专题：证明题．分析：（1）利用平行线的性质结合圆周角定理得出 =，进而得出答案；（2）首先得出△ADP∽△DBC，进而利用相似三角形的性质得出答案；（3）利用相似三角形的判定方法得出△ABP∽△DBA，进而求出AB2=DB•PB，再利用（2）中所求得出答案．解答：证明：（1）∵AD∥BC， ∴∠ADB=∠BDC， ∴=，∴AB=BC；（2）∵∠APB=∠BAD，∠BAD+∠BCD=180°，∠APB+∠APD=180°， ∴∠BCD=∠APD，又∵∠ADB=∠CBD， ∴△ADP∽△DBC， ∴=，∴DP•BD=AD•BC；（3）∵∠APB=∠BAD，∠BAD=∠BPA， ∴△ABP∽△DBA， ∴=，∴AB2=DB•PB， ∴AB2+AD•BC=DB•PB+AD•BC ∵由（2）得：DP•BD=AD•BC， ∴AB2+AD•BC=DB•PB+DP•BD=DB（PB+DP）=DB2，即BD2=AB2+AD•BC．点评：此题主要考查了相似三角形的判定与性质以及圆周角定理，熟练应用相似三角形的判定与性质是解题关键．　28．（9分）（2015•大庆）已知二次函数y=x2+bx﹣4的图象与y轴的交点为C，与x轴正半轴的交点为A，且tan∠ACO= （1）求二次函数的解析式；（2）P为二次函数图象的顶点，Q为其对称轴上的一点，QC平分∠PQO，求Q点坐标；（3）是否存在实数x1、x2（x1＜x2），当x1≤x≤x2时，y的取值范围为 ≤y≤ 若存在，直接写在x1，x2的值；若不存在，说明理由．？考点：二次函数综合题．分析：（1）首先根据tan∠ACO= ，求出OA的值，即可判断出A点的坐标；然后把A 点的坐标代入y=x2+bx﹣4，求出b的值，即可判断出二次函数的解析式．（2）首先根据Q为抛物线对称轴上的一点，设点Q的坐标为（﹣ ，n）；然后根据∠OQC=∠CQP、∠CQP=∠OCQ，可得∠OQC=∠OCQ，所以OQ=OC，据此求出n的值，进而判断出Q点坐标即可．（3）根据题意，分3种情况：①当x1≤x2≤﹣ 时；②当x1≤﹣ ≤x2时；③当﹣ ＜x1≤x2时；然后根据二次函数的最值的求法，求出满足题意的实数x1、x2（x1 ＜x2），使得当x1≤x≤x2时，y的取值范围为 ≤y≤ 即可．解答：解：（1）如图1，连接AC，，∵二次函数y=x2+bx﹣4的图象与y轴的交点为C， ∴C点的坐标为（0，﹣4）， ∵tan∠ACO= ， ∴，又∵OC=4， ∴OA=1， ∴A点的坐标为（1，0），把A（1，0）代入y=x2+bx﹣4，可得0=1+b﹣4，解得b=3， ∴二次函数的解析式是：y=x2+3x﹣4．（2）如图2，，∵y=x2+3x﹣4， ∴抛物线的对称轴是：x=﹣ ， ∵Q为抛物线对称轴上的一点， ∴设点Q的坐标为（﹣ ，n）， ∵抛物线的对称轴平行于y轴， ∴∠CQP=∠OCQ，又∵∠OQC=∠CQP， ∴∠OQC=∠OCQ， ∴OQ=OC， ∴，∴，解得n=± ，∴Q点坐标是（﹣ ，）或（﹣ ，﹣ ）．（3）①当x1≤x2≤﹣ 时，二次函数y=x2+3x﹣4单调递减， ∵y的取值范围为 ≤y≤ ，∴由+3×1﹣4= 解得x1=﹣3，﹣2，2， +3×2﹣4= ，由，解得x2=﹣3，﹣2，2， ∵x1≤x2≤﹣ ， ∴②当x1≤﹣ ≤x2时， Ⅰ、当﹣ 时，可得x1+x2≤﹣3， ∵y的取值范围为 ≤y≤ ，∴由（1），可得，由（2），可得x1=﹣3，﹣2，2， ∵x1≤﹣ ＜x2，，∴没有满足题意的x1、x2． Ⅱ、当﹣ 时，可得x1+x2＞﹣3， ∵y的取值范围为 ≤y≤ ，∴解得 ∵x1+x2= ≈﹣1.98﹣1.92=﹣3.9＜﹣3， ∴没有满足题意的x1、x2． ③当﹣ ＜x1≤x2时，二次函数y=x2+3x﹣4单调递增， ∵y的取值范围为 ≤y≤ ，∴（1）×x2﹣（2）×x1，可得（x1﹣x2）（x1x2+4）=0， ∵x1﹣x2≠0， ∴x1x2+4=0， ∴…（1），把（3）代入（1），可得，∵∴，，∴∵，，∴没有满足题意的x1、x2．综上，可得 x1=﹣3，x2=﹣2时，当x1≤x≤x2时，y的取值范围为 ≤y≤ ．点评：（1）此题主要考查了二次函数综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力．（2）此题还考查了待定系数法求二次函数的解析式的方法，以及二次函数的最值的求法，要熟练掌握．