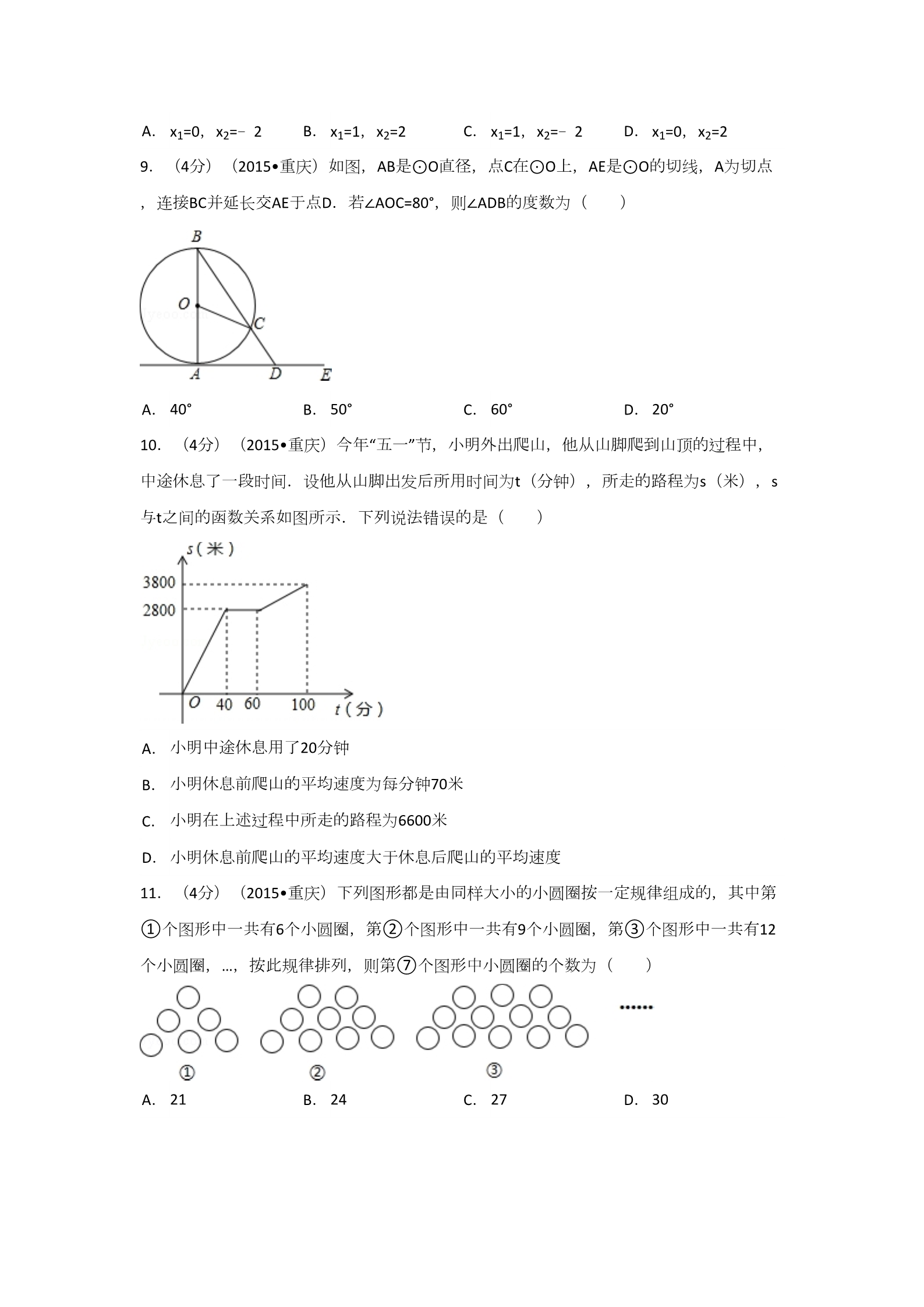
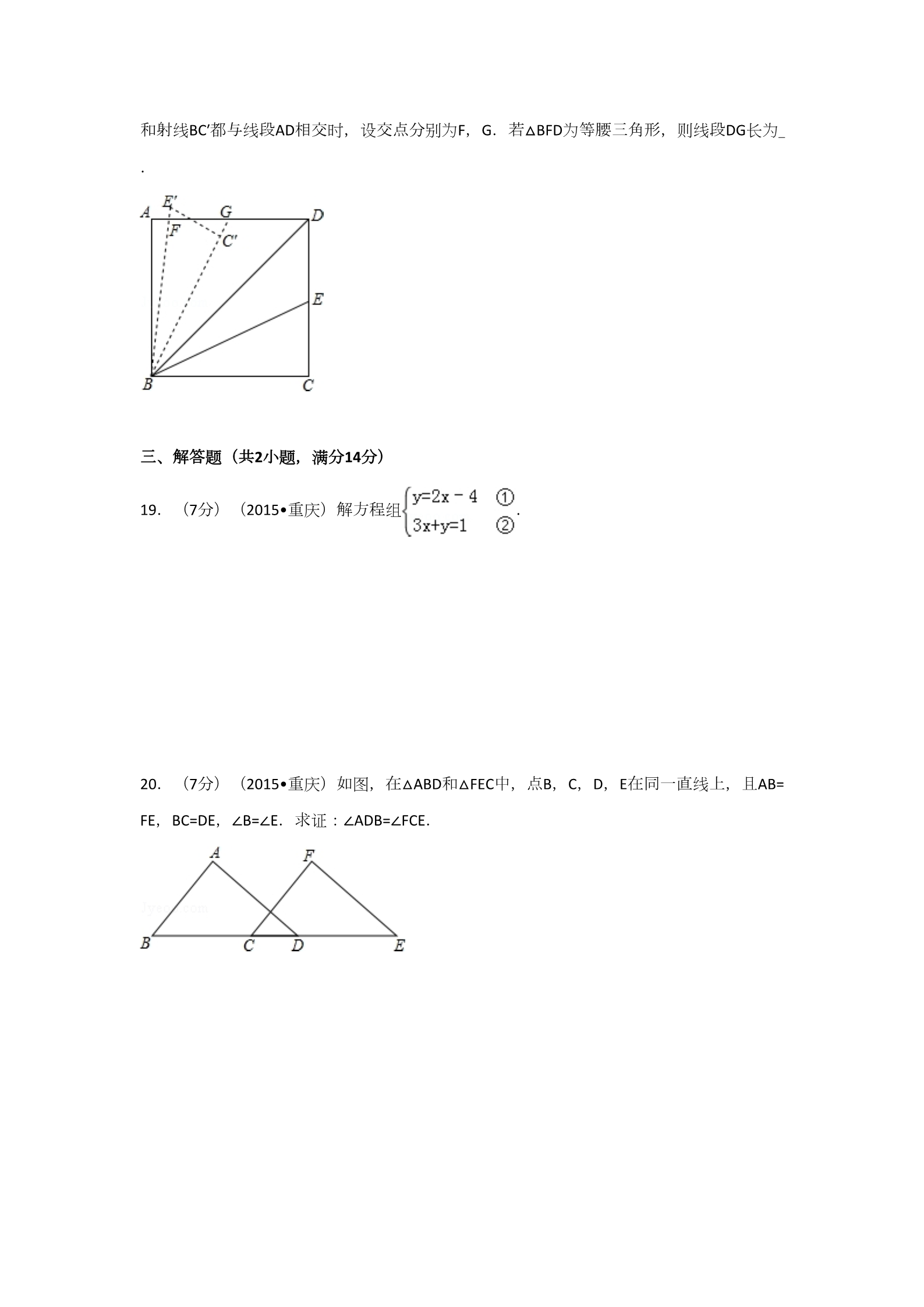
2015年重庆市中考数学试卷(A卷)（含解析版）

2015年重庆市中考数学试卷（A卷）一、选择题（共12小题，每小题4分，满分48分） 1．（4分）（2015•重庆）在﹣4，0，﹣1，3这四个数中，最大的数是（　　） ﹣4 ﹣1 　A． 03D． B． C． 2．（4分）（2015•重庆）下列图形是轴对称图形的是（　　） ABC　　　．　　　　　　　　．　　　　　　　．　　　　　　　　 D3．（4分）（2015•重庆）化简的结果是（　　） C．　A． B． D． D． 42324．（4分）（2015•重庆）计算（a2b）3的结果是（　　） 6323536　A． B． C． a b a b a b a b 5．（4分）（2015•重庆）下列调查中，最适合用普查方式的是（　　）调查一批电视机的使用寿命情况　A．调查某中学九年级一班学生的视力情况调查重庆市初中学生每天锻炼所用的时间情况调查重庆市初中学生利用网络媒体自主学习的情况　B．　C．　D． 6．（4分）（2015•重庆）如图，直线AB∥CD，直线EF分别与直线AB，CD相交于点G，H．若∠1=135°，则∠2的度数为（　　）　A． 65° 55° 45° 35° D． B． C． 7．（4分）（2015•重庆）在某校九年级二班组织的跳绳比赛中，第一小组五位同学跳绳的个数分别为198，230，220，216，209，则这五个数据的中位数为（　　）　A． 220 218 216 209 D． B． C． 8．（4分）（2015•重庆）一元二次方程x2﹣2x=0的根是（　　）　A． B． C． D． x1=0，x2=2 x1=0，x2=﹣2 x1=1，x2=2 x1=1，x2=﹣2 9．（4分）（2015•重庆）如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D．若∠AOC=80°，则∠ADB的度数为（　　）　A． 40° 50° 60° 20° D． B． C． 10．（4分）（2015•重庆）今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用时间为t（分钟），所走的路程为s（米），s 与t之间的函数关系如图所示．下列说法错误的是（　　）小明中途休息用了20分钟　A．小明休息前爬山的平均速度为每分钟70米小明在上述过程中所走的路程为6600米　B．　C．　D．小明休息前爬山的平均速度大于休息后爬山的平均速度 11．（4分）（2015•重庆）下列图形都是由同样大小的小圆圈按一定规律组成的，其中第 ①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12 个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（　　）　A． 21 24 27 30 D． B． C． 12．（4分）（2015•重庆）如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与 x轴平行，A，B两点的纵坐标分别为3，1．反比例函数y= 的图象经过A，B两点，则菱形AB CD的面积为（　　）　A． 24B． C． D． 42　二、填空题（共6小题，每小题4分，满分24分） 13．（4分）（2015•重庆）我国“南仓”级远洋综合补给舱满载排水量为37000吨，把数3700 0用科学记数法表示为　　　　　　． 14．（4分）（2015•重庆）计算：20150﹣|2|=　　　　　　． 15．（4分）（2015•重庆）已知△ABC∽△DEF，△ABC与△DEF的相似比为4：1，则△ABC与△ DEF对应边上的高之比为　　　　　　． 16．（4分）（2015•重庆）如图，在等腰直角三角形ABC中，∠ACB=90°，AB=4 ．以A为圆心，AC长为半径作弧，交AB于点D，则图中阴影部分的面积是　　　　　　．（结果保留π） 17．（4分）（2015•重庆）从﹣3，﹣2，﹣1，0，4这五个数中随机抽取一个数记为a，a的值既是不等式组的解，又在函数y= 的自变量取值范围内的概率是　　　　　　．18．（4分）（2015•重庆）如图，在矩形ABCD中，AB=4 ，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′ 和射线BC′都与线段AD相交时，设交点分别为F，G．若△BFD为等腰三角形，则线段DG长为　　　　　　．　三、解答题（共2小题，满分14分） 19．（7分）（2015•重庆）解方程组．　20．（7分）（2015•重庆）如图，在△ABD和△FEC中，点B，C，D，E在同一直线上，且AB= FE，BC=DE，∠B=∠E．求证：∠ADB=∠FCE．　　四、解答题（共4小题，满分40分） 21．（10分）（2015•重庆）计算：（1）y（2x﹣y）+（x+y）2；（2）（y﹣1﹣ ）÷ ．　22．（10分）（2015•重庆）为贯彻政府报告中“全民创新，万众创业”的精神，某镇对辖区内所有的小微企业按年利润w（万元）的多少分为以下四个类型：A类（w＜10），B类（1 0≤w＜20），C类（20≤w＜30），D类（w≥30），该镇政府对辖区内所有小微企业的相关信息进行统计后，绘制成以下条形统计图和扇形统计图，请你结合图中信息解答下列问题：（1）该镇本次统计的小微企业总个数是　　　　　　，扇形统计图中B类所对应扇形圆心角的度数为　　　　　　度，请补全条形统计图；（2）为了进一步解决小微企业在发展中的问题，该镇政府准备召开一次座谈会，每个企业派一名代表参会．计划从D类企业的4个参会代表中随机抽取2个发言，D类企业的4个参会代表中有2个来自高新区，另2个来自开发区．请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率．　23．（10分）（2015•重庆）如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数称为“和谐数”．例如自然数12321，从最高位到个位依次排出的一串数字是：1，2，3，2， 1，从个位到最高位依次排出的一串数字仍是：1，2，3，2，1，因此12321是一个“和谐数” ，再加22，545，3883，345543，…，都是“和谐数”．（1）请你直接写出3个四位“和谐数”；请你猜想任意一个四位“和谐数”能否被11整除？并说明理由；（2）已知一个能被11整除的三位“和谐数”，设其个位上的数字x（1≤x≤4，x为自然数），十位上的数字为y，求y与x的函数关系式．　24．（10分）（2015•重庆）某水库大坝的横截面是如图所示的四边形ABCD，其中AB∥CD ，大坝顶上有一瞭望台PC，PC正前方有两艘渔船M，N．观察员在瞭望台顶端P处观测到渔船M的俯角α为31°，渔船N的俯角β为45°．已知MN所在直线与PC所在直线垂直，垂足为E，且PE长为30米．（1）求两渔船M，N之间的距离（结果精确到1米）；（2）已知坝高24米，坝长100米，背水坡AD的坡度i=1：0.25，为提高大坝防洪能力，请施工队将大坝的背水坡通过填筑土石方进行加固，坝底BA加宽后变为BH，加固后背水坡DH的坡度i=1：1.75，施工队施工10天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的2倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：tan31°≈0.60，sin31°≈0.52）　　五、解答题（共2小题，满分24分） 25．（12分）（2015•重庆）如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE的垂线，过点A作AB的垂线，两垂线交于点D，连接DB，点F是BD 的中点，DH⊥AC，垂足为H，连接EF，HF．（1）如图1，若点H是AC的中点，AC=2 ，求AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想：△CEF是否是等边三角形？若是，请证明；若不是，说明理由．　26．（12分）（2015•重庆）如图1，在平面直角坐标系中，抛物线y=﹣ x2+ x+3 交x 轴于A，B两点（点A在点B的左侧），交y轴于点W，顶点为C，抛物线的对称轴与x轴的交点为D．（1）求直线BC的解析式；（2）点E（m，0），F（m+2，0）为x轴上两点，其中2＜m＜4，EE′，FF′分别垂直于x轴，交抛物线于点E′，F′，交BC于点M，N，当ME′+NF′的值最大时，在y轴上找一点R，使|RF′﹣ RE′|的值最大，请求出R点的坐标及|RF′﹣RE′|的最大值；（3）如图2，已知x轴上一点P（，0），现以P为顶点，2 为边长在x轴上方作等边三角形QPG，使GP⊥x轴，现将△QPG沿PA方向以每秒1个单位长度的速度平移，当点P到达点A时停止，记平移后的△QPG为△Q′P′G′．设△Q′P′G′与△ADC的重叠部分面积为s．当Q′到x轴的距离与点Q′到直线AW的距离相等时，求s的值．　　2015年重庆市中考数学试卷（A卷）参考答案与试题解析　一、选择题（共12小题，每小题4分，满分48分） 1．（4分）（2015•重庆）在﹣4，0，﹣1，3这四个数中，最大的数是（　　） ﹣4 ﹣1 　A． 03D． B． C．有理数大小比较．菁优网版权所有考点：先计算|﹣4|=4，|﹣1|=1，根据负数的绝对值越大，这个数越小得﹣4＜﹣1，再根分析：据正数大于0，负数小于0得到﹣4＜﹣1＜0＜3．解：∵|﹣4|=4，|﹣1|=1，解答：∴﹣4＜﹣1， ∴﹣4，0，﹣1，3这四个数的大小关系为﹣4＜﹣1＜0＜3．故选D．点评本题考查了有理数大小比较：正数大于0，负数小于0；负数的绝对值越大，这个数：　越小． 2．（4分）（2015•重庆）下列图形是轴对称图形的是（　　）　A． B． C． D．轴对称图形．菁优网版权所有考点：根据轴对称图形的概念求解．分析：解：A、是轴对称图形，故正确；解答 B、不是轴对称图形，故错误； C、不是轴对称图形，故错误； D、不是轴对称图形，故错误．故选A．：点评本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．：　3．（4分）（2015•重庆）化简的结果是（　　） C．　A． B． D． 2423二次根式的性质与化简．菁优网版权所有考点：直接利用二次根式的性质化简求出即可．分析：解答：解： =2 ．故选：B．点评此题主要考查了二次根式的性质与化简，正确化简二次根式是解题关键．：　4．（4分）（2015•重庆）计算（a2b）3的结果是（　　） 6323536　A． B． C． D． a b a b a b a b 幂的乘方与积的乘方．菁优网版权所有考点：根据幂的乘方和积的乘方的运算方法：①（am）n=amn（m，n是正整数）；②（ab ）n=anbn（n是正整数）；求出（a2b）3的结果是多少即可．分析：解：（a2b）3 =（a2）3•b3 =a6b3 解答：即计算（a2b）3的结果是a6b3．故选：A．点评此题主要考查了幂的乘方和积的乘方，要熟练掌握，解答此题的关键是要明确：① （am）n=amn（m，n是正整数）；②（ab）n=anbn（n是正整数）．：　5．（4分）（2015•重庆）下列调查中，最适合用普查方式的是（　　）调查一批电视机的使用寿命情况　A．调查某中学九年级一班学生的视力情况调查重庆市初中学生每天锻炼所用的时间情况调查重庆市初中学生利用网络媒体自主学习的情况　B．　C．　D．全面调查与抽样调查．菁优网版权所有考点：由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到分析：的调查结果比较近似．解：A、调查一批电视机的使用寿命情况，调查局有破坏性，适合抽样调查，故A不解答：符合题意； B、调查某中学九年级一班学生的视力情况，适合普查，故B符合题意； C、调查重庆市初中学生每天锻炼所用的时间情况，调查范围广，适合抽样调查，故 C不符合题意； D、调查重庆市初中学生利用网络媒体自主学习的情况，适合抽样调查，故D不符合题意；故选：B．点评本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．：　6．（4分）（2015•重庆）如图，直线AB∥CD，直线EF分别与直线AB，CD相交于点G，H．若∠1=135°，则∠2的度数为（　　）　A． 65° 55° 45° 35° D． B． C．平行线的性质．菁优网版权所有考点：根据平行线的性质求出∠2的度数即可．分析：解答解：∵AB∥CD，∠1=135°， ∴∠2=180°﹣135°=45°．故选C．：点评本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．：　7．（4分）（2015•重庆）在某校九年级二班组织的跳绳比赛中，第一小组五位同学跳绳的个数分别为198，230，220，216，209，则这五个数据的中位数为（　　）　A． 220 218 216 209 D． B． C．考点中位数．菁优网版权所有：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均分析：数）为中位数．解：先对这组数据按从小到大的顺序重新排序：198，209，216，220，230．解答：位于最中间的数是216，则这组数的中位数是216．故选C．点评本题属于基础题，考查了确定一组数据的中位数的能力．注意找中位数的时候一定要先排好顺序，然后根据奇数和偶数的个数来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．：　8．（4分）（2015•重庆）一元二次方程x2﹣2x=0的根是（　　）　A． B． C． D． x1=0，x2=2 x1=0，x2=﹣2 x1=1，x2=2 x1=1，x2=﹣2 考点解一元二次方程-因式分解法．菁优网版权所有：分析先分解因式，即可得出两个一元一次方程，求出方程的解即可．：解答解：x2﹣2x=0，：x（x﹣2）=0， x=0，x﹣2=0， x1=0，x2=2，故选D．点评本题考查了解一元二次方程的应用，解此题的关键是能把一元二次方程转化成一元一次方程，难度适中．：　9．（4分）（2015•重庆）如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D．若∠AOC=80°，则∠ADB的度数为（　　）　A． 40° 50° 60° 20° D． B． C．切线的性质．菁优网版权所有考点：分析：由AB是⊙O直径，AE是⊙O的切线，推出AD⊥AB，∠DAC=∠B= ∠AOC=40°，推出∠AOD =50°．解：∵AB是⊙O直径，AE是⊙O的切线， ∴∠BAD=90°，解答：∵∠B= ∠AOC=40°， ∴∠ADB=90°﹣∠B=50°，故选B．点评本题主要考查圆周角定理、切线的性质，解题的关键在于连接AC，构建直角三角形：　，求∠B的度数． 10．（4分）（2015•重庆）今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用时间为t（分钟），所走的路程为s（米），s 与t之间的函数关系如图所示．下列说法错误的是（　　）小明中途休息用了20分钟　A．小明休息前爬山的平均速度为每分钟70米小明在上述过程中所走的路程为6600米　B．　C．　D．小明休息前爬山的平均速度大于休息后爬山的平均速度一次函数的应用．菁优网版权所有考点：根据函数图象可知，小明40分钟爬山2800米，40～60分钟休息，60～100分钟爬山（ 3800﹣2800）米，爬山的总路程为3800米，根据路程、速度、时间的关系进行解答即可．分析：解：A、根据图象可知，在40～60分钟，路程没有发生变化，所以小明中途休息的时间为：60﹣40=20分钟，故正确；解答：B、根据图象可知，当t=40时，s=2800，所以小明休息前爬山的平均速度为：2800÷4 0=70（米/分钟），故B正确； C、根据图象可知，小明在上述过程中所走的路程为3800米，故错误； D、小明休息后的爬山的平均速度为：（3800﹣2800）÷（100﹣60）=25（米/分），小明休息前爬山的平均速度为：2800÷40=70（米/分钟）， 70＞25，所以小明休息前爬山的平均速度大于休息后爬山的平均速度，故正确；故选：C．点评本题考查了函数图象，解决本题的关键是读懂函数图象，获取信息，进行解决问题：　．11．（4分）（2015•重庆）下列图形都是由同样大小的小圆圈按一定规律组成的，其中第 ①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12 个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（　　）　A． 21 24 27 30 D． B． C．规律型：图形的变化类．菁优网版权所有考点：仔细观察图形，找到图形中圆形个数的通项公式，然后代入n=7求解即可．分析：解：观察图形得：解答：第1个图形有3+3×1=6个圆圈，第2个图形有3+3×2=9个圆圈，第3个图形有3+3×3=12个圆圈， …第n个图形有3+3n=3（n+1）个圆圈，当n=7时，3×（7+1）=24，故选B．点评本题考查了图形的变化类问题，解题的关键是仔细观察图形并找到图形变化的通项公式，难度不大．：　12．（4分）（2015•重庆）如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与 x轴平行，A，B两点的纵坐标分别为3，1．反比例函数y= 的图象经过A，B两点，则菱形AB CD的面积为（　　）　A． 24B． C． D． 42菱形的性质；反比例函数图象上点的坐标特征．菁优网版权所有考点：过点A作x轴的垂线，与CB的延长线交于点E，根据A，B两点的纵坐标分别为3，1，可得出横坐标，即可求得AE，BE，再根据勾股定理得出AB，根据菱形的面积公式：底乘高即可得出答案．分析：解：过点A作x轴的垂线，与CB的延长线交于点E，解答：∵A，B两点在反比例函数y= 的图象上且纵坐标分别为3，1， ∴A，B横坐标分别为1，3， ∴AE=2，BE=2， ∴AB=2 ，S菱形ABCD=底×高=2 ×2=4 ，故选D．点评本题考查了菱形的性质以及反比例函数图象上点的坐标特征，熟记菱形的面积公式是解题的关键．：　二、填空题（共6小题，每小题4分，满分24分） 13．（4分）（2015•重庆）我国“南仓”级远洋综合补给舱满载排水量为37000吨，把数3700 0用科学记数法表示为　3.7×104　．科学记数法—表示较大的数．菁优网版权所有考点：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解：将37000用科学记数法表示为3.7×104．分析：解答：故答案为：3.7×104．点评此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a |＜10，n为整数，表示时关键要正确确定a的值以及n的值．：　14．（4分）（2015•重庆）计算：20150﹣|2|=　﹣1　．实数的运算；零指数幂．菁优网版权所有考点：专题计算题．：原式第一项利用零指数幂法则计算，第二项利用绝对值的代数意义化简，计算即可得到结果．分析：解：原式=1﹣2 =﹣1．解答：故答案为：﹣1．点评此题考查了实数的运算，熟练掌握运算法则是解本题的关键．：　15．（4分）（2015•重庆）已知△ABC∽△DEF，△ABC与△DEF的相似比为4：1，则△ABC与△ DEF对应边上的高之比为　4：1　．相似三角形的性质．菁优网版权所有考点：根据相似三角形的对应边上的高之比等于相似比得出即可．分析：解：∵△ABC∽△DEF，△ABC与△DEF的相似比为4：1， ∴△ABC与△DEF对应边上的高之比是4：1，故答案为：4：1．解答：点评本题考查了相似三角形的性质的应用，能熟练地运用相似三角形的性质进行计算是解此题的关键，注意：相似三角形的对应边上的高之比等于相似比．：　16．（4分）（2015•重庆）如图，在等腰直角三角形ABC中，∠ACB=90°，AB=4 ．以A为圆心，AC长为半径作弧，交AB于点D，则图中阴影部分的面积是　8﹣2π　．（结果保留π）扇形面积的计算；等腰直角三角形．菁优网版权所有考点：根据等腰直角三角形性质求出∠A度数，解直角三角形求出AC和BC，分别求出△ACB 的面积和扇形ACD的面积即可．分析：解答解：∵△ACB是等腰直角三角形ABC中，∠ACB=90°， ∴∠A=∠B=45°，：∵AB=4 ，∴AC=BC=AB×sin45°=4， ∴S△ACB ===8，S扇形ACD ==2π， ∴图中阴影部分的面积是8﹣2π，故答案为：8﹣2π．点评本题考查了扇形的面积，三角形的面积，解直角三角形，等腰直角三角形性质的应用，解此题的关键是能求出△ACB和扇形ACD的面积，难度适中．：　17．（4分）（2015•重庆）从﹣3，﹣2，﹣1，0，4这五个数中随机抽取一个数记为a，a的值既是不等式组的解，又在函数y= 的自变量取值范围内的概率是　　．概率公式；解一元一次不等式组；函数自变量的取值范围．菁优网版权所有考点：分析：由a的值既是不等式组的解，又在函数y= 的自变量取值范围内的有﹣3，﹣2，可直接利用概率公式求解即可求得答案．解答：解：∵不等式组的解集是：﹣ ＜x＜， ∴a的值既是不等式组的解的有：﹣3，﹣2，﹣1，0， ∵函数y= 的自变量取值范围为：2×2+2x≠0，的自变量取值范围内的有﹣3，﹣2，4； ∴在函数y= ∴a的值既是不等式组的解，又在函数y= 的解，又在函数y= 的自变量取值范围的自变量取值范围内的有：﹣3，﹣2； ∴a的值既是不等式组内的概率是：．故答案为：．点评此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．：　18．（4分）（2015•重庆）如图，在矩形ABCD中，AB=4 ，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′ 和射线BC′都与线段AD相交时，设交点分别为F，G．若△BFD为等腰三角形，则线段DG长为　　．旋转的性质．菁优网版权所有考点：根据角平分线的性质，可得CE的长，根据旋转的性质，可得BC′=BC，E′C′=EC；根据等腰三角形，可得FD、FB的关系，根据勾股定理，可得BF的长，根据正切函数，可得tan∠ABF，tan∠FBG的值，根据三角函数的和差，可得AG的长，根据有理数的减法，可得答案．分析：解：作FK⊥BC′于K点，如图：解答：在Rt△ABD中，由勾股定理，得 BD= ==14 设DE=x，CE=4 ﹣x，由BE平分∠DBC，得 =，即 =．解得x= ，EC= ．在Rt△BCE中，由勾股定理，得 BE= 由旋转的性质，得 ==．BE′=BE= ，BC′=BC=10，E′C′=EC= ．△BFD是等腰三角形，BF=FD=x，在Rt△ABF中，由勾股定理，得 x2=（4 ）2+（10﹣x）2，解得x= ，AF=10﹣ = ． tan∠ABF= ==，tan∠FBG= ==，tan∠ABG=tan（∠ABF+∠FBG）= ==，tan∠ABG= =，AG= DG=AD﹣AG=10﹣ 故答案为：点评本题考查了旋转的性质，利用了勾股定理，旋转的性质，正切函数的定义，利用三 ×4 =，==，．角函数的和差得出AG的长是解题关键．：　三、解答题（共2小题，满分14分） 19．（7分）（2015•重庆）解方程组．解二元一次方程组．菁优网版权所有计算题．考点：专题：方程组利用代入消元法求出解即可．分析：解答：解：，①代入②得：3x+2x﹣4=1，解得：x=1，把x=1代入①得：y=﹣2，则方程组的解为．点评此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与：　加减消元法． 20．（7分）（2015•重庆）如图，在△ABD和△FEC中，点B，C，D，E在同一直线上，且AB= FE，BC=DE，∠B=∠E．求证：∠ADB=∠FCE．全等三角形的判定与性质．菁优网版权所有考点：专题证明题．：根据等式的性质得出BD=CE，再利用SAS得出：△ABD与△FEC全等，进而得出∠ADB=∠ 分析：FCE．证明：∵BC=DE， ∴BC+CD=DE+CD，即BD=CE，解答：在△ABD与△FEC中，，∴△ABD≌△FEC（SAS）， ∴∠ADB=∠FCE．点评此题考查全等三角形的判定和性质，关键是根据等式的性质得出BD=CE，再利用全等三角形的判定和性质解答．：　四、解答题（共4小题，满分40分） 21．（10分）（2015•重庆）计算：（1）y（2x﹣y）+（x+y）2；（2）（y﹣1﹣ ）÷ ．考点分式的混合运算；整式的混合运算．菁优网版权所有：专题：计算题．（1）原式利用单项式乘以多项式，以及完全平方公式化简，去括号合并即可得到结分析：果；（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．解：（1）原式=2xy﹣y2+x2+2xy+y2 =4xy+x2；解答：（2）原式= •=．点评此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．：　22．（10分）（2015•重庆）为贯彻政府报告中“全民创新，万众创业”的精神，某镇对辖区内所有的小微企业按年利润w（万元）的多少分为以下四个类型：A类（w＜10），B类（1 0≤w＜20），C类（20≤w＜30），D类（w≥30），该镇政府对辖区内所有小微企业的相关信息进行统计后，绘制成以下条形统计图和扇形统计图，请你结合图中信息解答下列问题：（1）该镇本次统计的小微企业总个数是　25　，扇形统计图中B类所对应扇形圆心角的度数为　72　度，请补全条形统计图；（2）为了进一步解决小微企业在发展中的问题，该镇政府准备召开一次座谈会，每个企业派一名代表参会．计划从D类企业的4个参会代表中随机抽取2个发言，D类企业的4个参会代表中有2个来自高新区，另2个来自开发区．请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率．列表法与树状图法；扇形统计图；条形统计图．菁优网版权所有考点：（1）由题意可得该镇本次统计的小微企业总个数是：4÷16%=25（个）；扇形统计图中B类所对应扇形圆心角的度数为： ×360°=72°；又由A类小微企业个数为：25﹣5 分析：﹣14﹣4=2（个）；即可补全条形统计图；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与所抽取的2 个发言代表都来自高新区的情况，再利用概率公式即可求得答案．解：（1）该镇本次统计的小微企业总个数是：4÷16%=25（个）；解答：扇形统计图中B类所对应扇形圆心角的度数为： ×360°=72°；故答案为：25，72； A类小微企业个数为：25﹣5﹣14﹣4=2（个）；补全统计图：（2）分别用A，B表示2个来自高新区的，用C，D表示2个来自开发区的．画树状图得： ∵共有12种等可能的结果，所抽取的2个发言代表都来自高新区的有2种情况， ∴所抽取的2个发言代表都来自高新区的概率为： = ．点评此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图．用到的知识点为：概率=所求情况数与总情况数之比．：　23．（10分）（2015•重庆）如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数称为“和谐数”．例如自然数12321，从最高位到个位依次排出的一串数字是：1，2，3，2， 1，从个位到最高位依次排出的一串数字仍是：1，2，3，2，1，因此12321是一个“和谐数” ，再加22，545，3883，345543，…，都是“和谐数”．（1）请你直接写出3个四位“和谐数”；请你猜想任意一个四位“和谐数”能否被11整除？并说明理由；（2）已知一个能被11整除的三位“和谐数”，设其个位上的数字x（1≤x≤4，x为自然数），十位上的数字为y，求y与x的函数关系式．因式分解的应用；规律型：数字的变化类．菁优网版权所有考点：（1）根据“和谐数”的定义（把一个自然数各数位上的数字从最高位到个位依次排出的一串数字，与从个位到最高位依次排出的一串数字完全相同）写出四个“和谐数” 分析：，设任意四位“和谐数”形式为：，根据和谐数的定义得到a=d，b=c，则 ===91a+10b为正整数，易证得任意四位“和谐数”都可以被11整除；（2）设能被11整除的三位“和谐数”为：，则 ===9x+y+ 为正整数．故y=2x（1≤x≤4，x为自然数）．解：（1）四位“和谐数”：1221，1331，1111，6666…（答案不唯一）任意一个四位“和谐数”都能被11整除，理由如下：解答：设任意四位“和谐数”形式为：，则满足：最高位到个位排列：d，c，b，a 个位到最高位排列：a，b，c，d．由题意，可得两组数据相同，则：a=d，b=c，则===91a+10b为正整数． ∴四位“和谐数”能被11整数，又∵a，b，c，d为任意自然数， ∴任意四位“和谐数”都可以被11整除；（2）设能被11整除的三位“和谐数”为：，则满足：个位到最高位排列：x，y，z．最高位到个位排列：z，y，x．由题意，两组数据相同，则：x=z，故故==101x+10y， ===9x+y+ 为正整数．故y=2x（1≤x≤4，x为自然数）．点评本题考查了因式分解的应用．解题的关键是弄清楚“和谐数”的定义，从而写出符合题意的数．：　24．（10分）（2015•重庆）某水库大坝的横截面是如图所示的四边形ABCD，其中AB∥CD ，大坝顶上有一瞭望台PC，PC正前方有两艘渔船M，N．观察员在瞭望台顶端P处观测到渔船M的俯角α为31°，渔船N的俯角β为45°．已知MN所在直线与PC所在直线垂直，垂足为E，且PE长为30米．（1）求两渔船M，N之间的距离（结果精确到1米）；（2）已知坝高24米，坝长100米，背水坡AD的坡度i=1：0.25，为提高大坝防洪能力，请施工队将大坝的背水坡通过填筑土石方进行加固，坝底BA加宽后变为BH，加固后背水坡DH的坡度i=1：1.75，施工队施工10天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的2倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：tan31°≈0.60，sin31°≈0.52）解直角三角形的应用-仰角俯角问题；分式方程的应用；解直角三角形的应用- 坡度坡角问题．菁优网版权所有考点：（1）在直角△PEN，利用三角函数即可求得ME的长，根据MN=EM﹣EN求解；（2）过点D作DN⊥AH于点N，利用三角函数求得AN和AH的长，进而求得△ADH的面积，得到需要填筑的土石方数，再根据结果比原计划提前20天完成，列方程求解．分析：解答：解：（1）在直角△PEN中，EN=PE=30m，ME= =50（m），则MN=EM﹣EN=20（m）．答：两渔船M、N之间的距离是20米；（2）过点D作DQ⊥AH于点Q．由题意得：tan∠DAB=4，tanH= ，在直角△DAQ中，AQ= 在直角△DHQ中，HQ= ===6（m）， =42（m）．故AH=HQ﹣AQ=42﹣6=36（m）． △ADH= AH•DQ=432（m2）． S故需要填筑的土石方是V=SL=432×100=43200（m3）．设原计划平均每天填筑xm3，则原计划每天填筑2xm3．天完成，则增加机械设备后，现在平均根据题意，得：10x+（）•2x=43200，解得：x=864．经检验x=864是原方程的解．答：施工队原计划平均每天填筑土石方864立方米．点评本题考查了仰角的定义以及坡度，要求学生能借助仰角构造直角三角形并解直角三：　角形．五、解答题（共2小题，满分24分） 25．（12分）（2015•重庆）如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE的垂线，过点A作AB的垂线，两垂线交于点D，连接DB，点F是BD 的中点，DH⊥AC，垂足为H，连接EF，HF．（1）如图1，若点H是AC的中点，AC=2 ，求AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想：△CEF是否是等边三角形？若是，请证明；若不是，说明理由．全等三角形的判定与性质；等边三角形的判定与性质；三角形中位线定理．菁优网版权所有考点：（1）根据直角三角形的性质和三角函数即可得到结果；分析：（2）如图1，连接AF，证出△DAE≌△ADH，△DHF≌△AEF，即可得到结果；（3）如图2，取AB的中点M，连接CM，FM，在Rt△ADE中，AD=2AE，根据三角形的中位线的性质得到AD=2FM，于是得到FM=AE，由∠CAE= ∠CAB=30°∠CMF=∠AMF﹣A MC=30°，证得△ACE≌△MCF，问题即可得证．解答解：（1）∵∠ACB=90°，∠BAC=60°，：∴∠ABC=30°， ∴AB=2AC=2×2 =4 ∵AD⊥AB，∠CAB=60°， ∴∠DAC=30°，，∵AH= AC= ∴AD= ，=2， =2 ∴BD= ；（2）如图1，连接AF， ∵AE是∠BAC角平分线， ∴∠HAE=30°， ∴∠ADE=∠DAH=30°，在△DAE与△ADH中，，∴△DAE≌△ADH， ∴DH=AE， ∵点F是BD的中点， ∴DF=AF， ∵∠EAF=∠EAB﹣∠FAB=30°﹣∠FAB ∠FDH=∠FDA﹣∠HDA=∠FDA﹣60°=（90°﹣∠FBA）﹣60°=30°﹣∠FBA， ∴∠EAF=∠FDH，在△DHF与△AEF中，，∴△DHF≌△AEF， ∴HF=EF；（3）如图2，取AB的中点M，连接CM，FM，在Rt△ADE中，AD=2AE， ∵DF=BF，AM=BM， ∴AD=2FM， ∴FM=AE， ∵∠ABC=30°， ∴AC=CM= AB=AM， ∵∠CAE= ∠CAB=30°∠CMF=∠AMF﹣∠AMC=30°，在△ACE与△MCF中，，∴△ACE≌△MCF， ∴CE=CF，∠ACE=∠MCF， ∵∠ACM=60°， ∴∠ECF=60°， ∴△CEF是等边三角形．点评本题考查了全等三角形的判定和性质，直角三角形的性质，等边三角形的判定，正确的作出辅助线构造全等三角形是解题的关键．：　26．（12分）（2015•重庆）如图1，在平面直角坐标系中，抛物线y=﹣ x2+ x+3 交x 轴于A，B两点（点A在点B的左侧），交y轴于点W，顶点为C，抛物线的对称轴与x轴的交点为D．（1）求直线BC的解析式；（2）点E（m，0），F（m+2，0）为x轴上两点，其中2＜m＜4，EE′，FF′分别垂直于x轴，交抛物线于点E′，F′，交BC于点M，N，当ME′+NF′的值最大时，在y轴上找一点R，使|RF′﹣ RE′|的值最大，请求出R点的坐标及|RF′﹣RE′|的最大值；（3）如图2，已知x轴上一点P（，0），现以P为顶点，2 为边长在x轴上方作等边三角形QPG，使GP⊥x轴，现将△QPG沿PA方向以每秒1个单位长度的速度平移，当点P到达点A时停止，记平移后的△QPG为△Q′P′G′．设△Q′P′G′与△ADC的重叠部分面积为s．当Q′到x轴的距离与点Q′到直线AW的距离相等时，求s的值．二次函数综合题．菁优网版权所有考点：（1）求出抛物线与x轴的交点坐标和顶点坐标，用待定系数法求解析式即可；（2）先求出E′、F′的坐标表示，然后求出E′M、F′N，用二次函数的顶点坐标求出当m =3时，ME′+NF′的值最大，得到E′、F′的坐标，再求出E′F′的解析式，当点R在直线E′F′ 与y轴的交点时，|RF′﹣RE′|的最大值，从而求出R点的坐标及|RF′﹣RE′|的最大值；（3）分类讨论Q点在∠CAB的角平分线或外角平分线上时，运用三角形相似求出相应线段，在求出△Q′P′G′与△ADC的重叠部分面积为S．分析：解：（1）令y=0，则﹣ x2+ x+3 =0，解答：解方程得：x=6或x=﹣2， ∴A（﹣2，0），B（6，0），又y=﹣ x2+ x+3 =﹣ （x﹣2）2+4 又顶点C（2，4 ），，设直线BC的解析式为：y=kx+b，代入B、C两点坐标得：，解得：，∴y=﹣ x+6 ；（2）如图1， ∵点E（m，0），F（m+2，0）， ∴E′（m，﹣ m2+ m+3 ），F′（m+2，﹣ m2+4 ）， ∴E′M=﹣ m2+ m+3 ﹣（﹣ m+6 ）=﹣ m2+2 m﹣3 F′N=﹣ m2+4 ﹣（﹣ m+4 ）=﹣ m2+ m，，∴E′M+F′N=﹣ m2+2 m﹣3 +（﹣ m2+ m）=﹣ m2+3 m﹣3 ，当m=﹣ =3时，E′M+F′N的值最大， ∴此时，E′（3，）F′（5，）， ∴直线E′F′的解析式为：y=﹣ x+ ∴R（0，），，根据勾股定理可得：RF′=10，RE′=6， ∴|RF′﹣RE′|的值最大值是4；（3）由题意得，Q点在∠CAB的角平分线或外角平分线上， ①如图2，当Q点在∠CAB的角平分线上时， Q′M=Q′N= ，AW= ∵△RMQ′∽△WOA，，∴∴RQ′= ∴RN= ，+，∵△ARN∽△AWO， ∵∴AN= ，∴DN=AD﹣AN=4﹣ ∴S= =，；②如图3，当Q点在∠CAB的外角平分线上时， ∵△Q′RN∽△WAO， ∴RQ′= ∴RM= ，﹣，∵△RAM∽△WOA， ∴AM= 在RtQ′MP′中，MP′= Q′M=3，，∴AP′=MP′﹣AM=3﹣ =，在Rt△AP′S中，P′S= AP′= ×，∴S= ．点评本题主要考查了待定系数法求函数解析式，二次函数的性质，三角形的三边关系，三角形相似的判定与性质以及数形结合和分类讨论思想的综合运用，此题牵扯知识面广，综合性强，难度较大．：