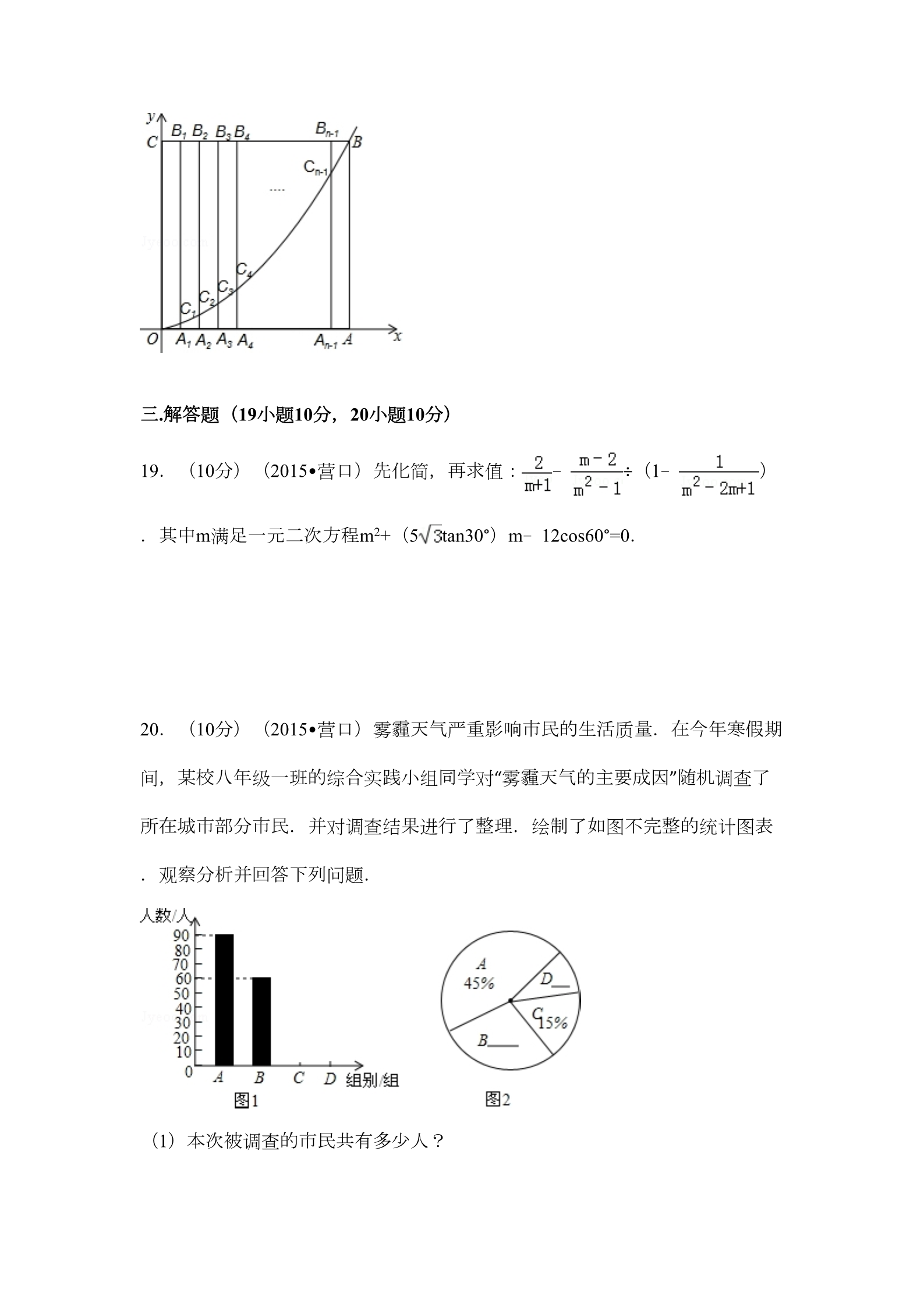
2015年辽宁省营口市中考数学试卷（含解析版）

2015年辽宁省营口市中考数学试卷一.选择题（每小题3分共30分，四个选项中只有一个选项是正确的） 1．（3分）（2015•营口）下列计算正确的是（　　）　 A． |﹣2|=﹣2 B． a2•a3=a6 C．（﹣3）﹣2= D． =3 2．（3分）（2015•营口）如图，是由若干个相同的小立方体搭成的几何体生物俯视图和左视图．则小立方体的个数可能是（　　）　 A． 5或6 B． 5或7 C． 4或5或6 D． 5或6或7 3．（3分）（2015•营口）函数y= 中自变量x的取值范围是（　　）　 A． x≥﹣3 B． x≠5 C． x≥﹣3或x≠5 D． x≥﹣3且x≠5 4．（3分）（2015•营口）▱ABCD中，对角线AC与BD交于点O，∠DAC=42°， ∠CBD=23°，则∠COD是（　　）　 A． 61° B． 63° C． 65° D． 67° 5．（3分）（2015•营口）云南鲁甸发生地震后，某社区开展献爱心活动，社区党员积极向灾区捐款，如图是该社区部分党员捐款情况的条形统计图，那么本次捐款钱数的众数和中位数分别是（　　）　 A． 100元，100元 B． 100元，200元　 C． 200元，100元 D． 200元，200元 6．（3分）（2015•营口）若关于x的分是方程 +=2有增根，则m的值是（　　）　 A． m=﹣1 B． m=0 C． m=3 D． m=0或m=3 7．（3分）（2015•营口）将弧长为2πcm，圆心角为120°的扇形围成一个圆锥的侧面，则这个圆锥的高及侧面积分别是（　　）　 A．　 C． 2 cm，6πcm2 D． cm，3πcm2 B． 2 cm，3πcm2 cm，6πcm2 8．（3分）（2015•营口）如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C（2，2），点D（3，1），则点D的对应点B的坐标是（　　）　 A．（4，2） B．（4，1） C．（5，2） D．（5，1） 9．（3分）（2015•营口）如图，在平面直角坐标系中，A（﹣3，1），以点O 为顶点作等腰直角三角形AOB，双曲线y1= 在第一象限内的图象经过点B．设直线AB的解析式为y2=k2x+b，当y1＞y2时，x的取值范围是（　　）　 A． ﹣5＜x＜1 B． 0＜x＜1或x＜﹣5 　 C． ﹣6＜x＜1 D． 0＜x＜1或x＜﹣6 10．（3分）（2015•营口）如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB 的度数是（　　）　 A． 25° B． 30° C． 35° D． 40° 二.填空题（每小题3分，共24分） 11．（3分）（2015•营口）分解因式：﹣a2c+b2c=　　　　　　． 12．（3分）（2015•营口）过度包装既浪费资源又污染环境．据测算，如果全国每年减少十分之一的包装纸用量，那么能减少3120000吨二氧化碳的排放量．把数据3120000用科学记数法表示为　　　　　　． 13．（3分）（2015•营口）不等式组的所有正整数解的和为　　　　　　．14．（3分）（2015•营口）圆内接正六边形的边心距为2 ，则这个正六边形的面积为　　　　　　cm2． 15．（3分）（2015•营口）如图，正方形的阴影部分是由四个直角边长都是1和 3的直角三角形组成的，假设可以在正方形内部随意取点，那么这个点取在阴影部分的概率为　　　　　　． 16．（3分）（2015•营口）某服装店购进单价为15元童装若干件，销售一段时间后发现：当销售价为25元时平均每天能售出8件，而当销售价每降低2元，平均每天能多售出4件，当每件的定价为　　　　　　元时，该服装店平均每天的销售利润最大． 17．（3分）（2015•营口）定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径，即损矩形外接圆的直径．如图，△ABC中，∠ABC=90°，以AC为一边向形外作菱形ACEF，点D是菱形ACEF对角线的交点，连接BD．若∠DBC=60°，∠ACB=15°，BD=2 ，则菱形ACEF的面积为　　　　　　． 18．（3分）（2015•营口）如图，边长为n的正方形OABC的边OA、OC分别在 x轴和y轴的正半轴上，A1、A2、A3、…、An﹣1为OA的n等分点，B1、B2、B3、… Bn﹣1为CB的n等分点，连接A1B1、A2B2、A3B3、…、An﹣1 Bn﹣1，分别交y= x2（ x≥0）于点C1、C2、C3、…、Cn﹣1，当B25C25=8C25A25时，则n=　　　　　　．　三.解答题（19小题10分，20小题10分） 19．（10分）（2015•营口）先化简，再求值： ﹣÷（1﹣ ）．其中m满足一元二次方程m2+（5 tan30°）m﹣12cos60°=0．　20．（10分）（2015•营口）雾霾天气严重影响市民的生活质量．在今年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．（1）本次被调查的市民共有多少人？（2）分别补全条形统计图和扇形统计图，并计算图2中区域B所对应的扇形圆心角的度数；（3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？组别 A百分比 45% m雾霾天气的主要成因工业污染 B汽车尾气排放炉烟气排放 CD15% n其他（滥砍滥伐等）　　四.解答题 21．（12分）（2015•营口）某化妆品专卖店，为了吸引顾客，在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动，凡购物满88元，均可得到一次摇奖的机会．已知在摇奖机内装有2个红球和2个白球，除颜色外其它都相同，摇奖者必须从摇奖机内一次连续摇出两个球，根据球的颜色决定送礼金券的多少（如表）甲种品牌化两白 . 乙种品牌化两白两红一红两红一红一白一白妆品球妆品球礼金券（元 6 12 6礼金券（元 12 612 ））（1）请你用列表法（或画树状图法）求一次连续摇出一红一白两球的概率；（2）如果一个顾客当天在本店购物满88元，若只考虑获得最多的礼品券，请你帮助分析选择购买哪种品牌的化妆品？并说明理由．　22．（12分）（2015•营口）如图，我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪，船长马上向我国渔政搜救中心发出求救信号，此时一艘渔政船正巡航到捕鱼船正西方向的B处，该渔政船收到渔政求救中心指令后前去救援，但两船之间有大片暗礁，无法直线到达，于是决定马上调整方向，先向北偏东6 0°方向以每小时30海里的速度航行半小时到达C处，同时捕鱼船低速航行到A点的正北1.5海里D处，渔政船航行到点C处时测得点D在南偏东53°方向上．（1）求CD两点的距离；（2）渔政船决定再次调整航向前去救援，若两船航速不变，并且在点E处相会合，求∠ECD的正弦值．（参考数据：sin53°≈ ，cos53°≈ ，tan53°≈ ） 23．（12分）（2015•营口）如图，点P是⊙O外一点，PA切⊙O于点A，AB是 ⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD= ，AC=8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．　24．（12分）（2015•营口）某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售，已知每天包装大黄米的质量是包装江米质量的倍，且每天包装大黄米和江米的质量之和为45千克．（1）求平均每天包装大黄米和江米的质量各是多少千克？（2）为迎接今年6月20日的“端午节”，该超市决定在前20天增加每天包装大黄米和江米的质量，二者的包装质量与天数的变化情况如图所示，节日后又恢复到原来每天的包装质量．分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式，并写出自变量的取值范围．（3）假设该超市每天都会将当天包装后的大黄米和江米全部售出，已知大黄米成本价为每千克7.9元，江米成本每千克9.5元，二者包装费用平均每千克均为0. 5元，大黄米售价为每千克10元，江米售价为每千克12元，那么在这20天中有哪几天销售大黄米和江米的利润之和大于120元？[总利润=售价额﹣成本﹣包装费用]．　25．（14分）（2015•营口）【问题探究】（1）如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD ，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．【深入探究】（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45° ，求BD的长．（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．　26．（14分）（2015•营口）如图1，一条抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，且当x=﹣1和x=3时，y的值相等，直线y= x﹣ 与抛物线有两个交点，其中一个交点的横坐标是6，另一个交点是这条抛物线的顶点M．（1）求这条抛物线的表达式．（2）动点P从原点O出发，在线段OB上以每秒1个单位长度的速度向点B运动，同时点Q从点B出发，在线段BC上以每秒2个单位长度的速度向点C运动，当一个点到达终点时，另一个点立即停止运动，设运动时间为t秒． ①若使△BPQ为直角三角形，请求出所有符合条件的t值； ②求t为何值时，四边形ACQP的面积有最小值，最小值是多少？（3）如图2，当动点P运动到OB的中点时，过点P作PD⊥x轴，交抛物线于点D ，连接OD，OM，MD得△ODM，将△OPD沿x轴向左平移m个单位长度（0＜m ＜2），将平移后的三角形与△ODM重叠部分的面积记为S，求S与m的函数关系式．　　2015年辽宁省营口市中考数学试卷参考答案与试题解析一.选择题（每小题3分共30分，四个选项中只有一个选项是正确的） 1．（3分）（2015•营口）下列计算正确的是（　　）　 A． |﹣2|=﹣2 B． a2•a3=a6 C．（﹣3）﹣2= D． =3 考点：同底数幂的乘法；绝对值；算术平方根；负整数指数幂．分析：分别根据绝对值的性质、同底数幂的乘法法则、负整数指数幂的运算法则及数的开方法则对各选项进行逐一计算即可．解答：解：A、原式=2≠﹣2，故本选项错误； B、原式=a5≠a6，故本选项错误； C、原式= ，故本选项正确； D、原式=2 ≠3 ，故本选项错误．故选C．点评：本题考查的是同底数幂的乘法，熟知绝对值的性质、同底数幂的乘法法则、负整数指数幂的运算法则及数的开方法则是解答此题的关键．　2．（3分）（2015•营口）如图，是由若干个相同的小立方体搭成的几何体生物俯视图和左视图．则小立方体的个数可能是（　　）　 A． 5或6 B． 5或7 C． 4或5或6 D． 5或6或7 考点：由三视图判断几何体．分析：易得这个几何体共有2层，由俯视图可得第一层立方体的个数，由左视图可得第二层最多和最少小立方体的个数，相加即可．解答：解：由俯视图易得最底层有4个小立方体，由左视图易得第二层最多有3个小立方体和最少有1个小立方体，那么小立方体的个数可能是5个或6个或7个．故选D．点评：本题考查了由三视图判断几何体，也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．注意俯视图中有几个正方形，底层就有几个小立方体．　3．（3分）（2015•营口）函数y= 中自变量x的取值范围是（　　）　 A． x≥﹣3 B． x≠5 C． x≥﹣3或x≠5 D． x≥﹣3且x≠5 考点：函数自变量的取值范围．分析：利用二次根式的性质以及分数的性质分别得出关系式求出即可．解答：解：由题意可得：x+3≥0，x﹣5≠0，解得：x≥﹣3且x≠5．故选：D．点评：此题主要考查了函数自变量的取值范围，熟练掌握二次根式的性质是解题关键．　4．（3分）（2015•营口）▱ABCD中，对角线AC与BD交于点O，∠DAC=42°， ∠CBD=23°，则∠COD是（　　）　 A． 61° B． 63° C． 65° D． 67° 考点：平行四边形的性质．分析：由平行四边形的性质可知：AD∥BC，进而可得∠DAC=∠BCA，再根据三角形外角和定理即可求出∠COD的度数．解答：解：∵四边形ABCD是平行四边形， ∴AD∥BC， ∴∠DAC=∠BCA=42°， ∴∠COD=∠CBD+∠BCA=65°，故选C．点评：本题考查了平行四边形的性质以及三角形的外角和定理，题目比较简单，解题的关键是灵活运用平行四边形的性质，将四边形的问题转化为三角形问题．　5．（3分）（2015•营口）云南鲁甸发生地震后，某社区开展献爱心活动，社区党员积极向灾区捐款，如图是该社区部分党员捐款情况的条形统计图，那么本次捐款钱数的众数和中位数分别是（　　）　 A． 100元，100元 B． 100元，200元 C． 200元，100元 D． 200元，200元考点：众数；条形统计图；中位数．分析：认真观察统计图，根据中位数和众数的定义求解即可．解答：解：从图中看出，捐100元的人数最多有18人，所以众数是100元，捐款人数为48人，中位数是第24、25的平均数，所以中位数是200元，故选：B．点评：本题考查众数与中位数的意义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），从统计图中获取正确的信息是解题的关键．　6．（3分）（2015•营口）若关于x的分是方程 +=2有增根，则m的值是（　　）　 A． m=﹣1 B． m=0 C． m=3 D． m=0或m=3 考点：分式方程的增根．分析：方程两边都乘以最简公分母（x﹣3），把分式方程化为整式方程，再根据分式方程的增根就是使最简公分母等于0的未知数的值求出x的值，然后代入进行计算即可求出m的值．解答：解：方程两边都乘以（x﹣3）得， 2﹣x﹣m=2（x﹣3）， ∵分式方程有增根， ∴x﹣3=0，解得x=3， ∴2﹣3﹣m=2（3﹣3），解得m=﹣1．故选A．点评：本题考查了分式方程的增根，增根问题可按如下步骤进行： ①让最简公分母为0确定增根； ②化分式方程为整式方程； ③把增根代入整式方程即可求得相关字母的值．　7．（3分）（2015•营口）将弧长为2πcm，圆心角为120°的扇形围成一个圆锥的侧面，则这个圆锥的高及侧面积分别是（　　）　 A． cm，6πcm2 cm，3πcm2 B． 2 cm，3πcm2 C． 2 cm，6πcm2 D．考点：圆锥的计算．分析：已知弧长为2πcm，圆心角为120°的扇形为4 cm，就可以求出扇形的半径，即圆锥的母线长，根据扇形的面积公式可求这个圆锥的侧面积，根据勾股定理可求出圆锥的高．解答：解：（2π×180）÷120π=3（cm）， 2π÷π÷2=1（cm）， =2 （cm）， =3π（cm2）．故这个圆锥的高是2 cm，侧面积是3πcm2．故选：B．点评：考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．　8．（3分）（2015•营口）如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C（2，2），点D（3，1），则点D的对应点B的坐标是（　　）　 A．（4，2） B．（4，1） C．（5，2） D．（5，1）考点：位似变换；坐标与图形性质．分析：设点B的坐标为（x，y），然后根据位似变换的性质列式计算即可得解．解答：解：设点B的坐标为（x，y）， ∵△ABE和△CDE是以点E为位似中心的位似图形， ∴=，=，解得x=5，y=2，所以，点B的坐标为（5，2）．故选C．点评：本题考查了位似变换，坐标与图形性质，灵活运用位似变换的性质并列出方程是解题的关键．　9．（3分）（2015•营口）如图，在平面直角坐标系中，A（﹣3，1），以点O 为顶点作等腰直角三角形AOB，双曲线y1= 在第一象限内的图象经过点B．设直线AB的解析式为y2=k2x+b，当y1＞y2时，x的取值范围是（　　）　 A． ﹣5＜x＜1 B． 0＜x＜1或x＜﹣5 C． ﹣6＜x＜1 D． 0＜x＜1或x＜﹣6 考点：反比例函数与一次函数的交点问题．专题：计算题．分析：由△AOB是等腰三角形，先求的点B的坐标，然后利用待定系数法可求得双曲线和直线的解析式，然后将将y1= 与y2= 联立，求得双曲线和直线的交点的横坐标，然后根据图象即可确定出x的取值范围．解答：解：如图所示： ∵△AOB为等腰直角三角形， ∴OA=OB，∠3+∠2=90°．又∵∠1+∠3=90°， ∴∠1=∠2． ∵点A的坐标为（﹣3，1）， ∴点B的坐标（1，3）．将B（1，3）代入反比例函数的解析式得：3= ， ∴k=3． ∴y1= 将A（﹣3，1），B（1，3）代入直线AB的解析式得：，解得：，∴直线AB的解析式为y2= ．将y1= 与y2= 联立得；，解得：，当y1＞y2时，双曲线位于直线线的上方， ∴x的取值范围是：x＜﹣6或0＜x＜1．故选：D．点评：本题主要考查了反比例函数和一次函数的交点问题，求得双曲线和直线的交点的横坐标是解题的关键，同时本题还考查了函数与不等式的关系：从函数的角度看，y1＞y2就是双曲线y1= 位于直线y2= 上方部分所有点的横坐标的集合；从不等式的角度来看y1＞y2就是求不等式＞的解集．　10．（3分）（2015•营口）如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB 的度数是（　　）　 A． 25° B． 30° C． 35° D． 40° 考点：轴对称-最短路线问题．分析：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N ，连接OC、OD、PM、PN、MN，由对称的性质得出PM=CM，OP=OC，∠CO A=∠POA；PN=DN，OP=OD，∠DOB=∠POB，得出∠AOB= ∠COD，证出△OC D是等边三角形，得出∠COD=60°，即可得出结果．解答：解：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示： ∵点P关于OA的对称点为C，关于OB的对称点为D， ∴PM=CM，OP=OC，∠COA=∠POA； ∵点P关于OB的对称点为D， ∴PN=DN，OP=OD，∠DOB=∠POB， ∴OC=OP=OD，∠AOB= ∠COD， ∵△PMN周长的最小值是5cm， ∴PM+PN+MN=5， ∴CM+DN+MN=5，即CD=5=OP， ∴OC=OD=CD，即△OCD是等边三角形， ∴∠COD=60°， ∴∠AOB=30°；故选：B．点评：本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质；熟练掌握轴对称的性质，证明三角形是等边三角形是解决问题的关键．　二.填空题（每小题3分，共24分） 11．（3分）（2015•营口）分解因式：﹣a2c+b2c=　﹣c（a+b）（a﹣b）　．考点：提公因式法与公式法的综合运用．分析：首先提公因式﹣c，然后利用平方差公式分解．解答：解：原式=﹣c（a2﹣b2）=﹣c（a+b）（a﹣b）．故答案是：﹣c（a+b）（a﹣b）．点评：本题考查了提公因式法，公式法分解因式，提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．　12．（3分）（2015•营口）过度包装既浪费资源又污染环境．据测算，如果全国每年减少十分之一的包装纸用量，那么能减少3120000吨二氧化碳的排放量．把数据3120000用科学记数法表示为　3.12×106　．考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：将3120000用科学记数法表示为3.12×106．故答案为：3.12×106．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中 1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　13．（3分）（2015•营口）不等式组 6　．的所有正整数解的和为　考点：一元一次不等式组的整数解．分析：先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求其整数解即可．解答：解：由 ﹣≤1，得 x≥1；由5x﹣2＜3（x+2），得 x＜4，不等式组的解集是1≤x＜4，不等式组的所有正整数解的和为1+2+3=6，故答案为：6．点评：本题考查了一元一次不等式组的解集，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．　14．（3分）（2015•营口）圆内接正六边形的边心距为2 ，则这个正六边形的面积为　24 　cm2．考点：正多边形和圆．分析：根据正六边形的特点，通过中心作边的垂线，连接半径，结合解直角三角形的有关知识解决．解答：解：如图，连接OA、OB；过点O作OG⊥AB于点G．在Rt△AOG中，OG=2 ，∠AOG=30°， ∵OG=OA•cos 30°， ∴OA= ==4， ∴这个正六边形的面积为6× ×4×2 =24 cm2．故答案为：24 点评：．此题主要考查正多边形的计算问题，根据题意画出图形，再根据正多边形的性质即锐角三角函数的定义解答即可．　15．（3分）（2015•营口）如图，正方形的阴影部分是由四个直角边长都是1和 3的直角三角形组成的，假设可以在正方形内部随意取点，那么这个点取在阴影部分的概率为　．考点：几何概率．分析：先求出正方形的面积，阴影部分的面积，再根据几何概率的求法即可得出答案．解答：解：∵S正方形= （3×2）2=18， S阴影=4× ×3×1=6， ∴这个点取在阴影部分的概率为： = ，故答案为：．点评：本题考查了几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．　16．（3分）（2015•营口）某服装店购进单价为15元童装若干件，销售一段时间后发现：当销售价为25元时平均每天能售出8件，而当销售价每降低2元，平均每天能多售出4件，当每件的定价为　22　元时，该服装店平均每天的销售利润最大．考点：二次函数的应用．分析：根据“利润=（售价﹣成本）×销售量”列出每天的销售利润y（元）与销售单价x （元）之间的函数关系式；把二次函数解析式转化为顶点式方程，利用二次函数图象的性质进行解答．解答：解：设定价为x元，根据题意得：y=（x﹣15）[8+2（25﹣x）] =﹣2×2+88x﹣870 ∴y=﹣2×2+88x﹣870， =﹣2（x﹣22）2+98 ∵a=﹣2＜0， ∴抛物线开口向下， ∴当x=22时，y最大值=98．故答案为：22．点评：此题题考查二次函数的实际应用，为数学建模题，借助二次函数解决实际问题，解决本题的关键是二次函数图象的性质．　17．（3分）（2015•营口）定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径，即损矩形外接圆的直径．如图，△ABC中，∠ABC=90°，以AC为一边向形外作菱形ACEF，点D是菱形ACEF对角线的交点，连接BD．若∠DBC=60°，∠ACB=15°，BD=2 ，则菱形ACEF的面积为　12 　．考点：菱形的性质；圆周角定理；解直角三角形．专题：新定义．分析：首先取AC的中点G，连接BG、DG，再根据∠ADC=90°，∠ABC=90°，判断出A 、B、C、D四点共圆，点G是圆心；然后求出∠BGD=90°，即可判断出△BGD是等腰直角三角形；最后解直角三角形，分别求出AD、CD的值，再根据三角形的面积的求法，求出菱形ACEF的面积为多少即可．解答：解：如图1，取AC的中点G，连接BG、DG， ∵四边形ACEF是菱形，，∴AE⊥CF， ∴∠ADC=90°，又∵∠ABC=90°， ∴A、B、C、D四点共圆，点G是圆心， ∴∠ACD=∠ABD=90°﹣∠DBC=90°﹣60°=30°， ∵∠AGB=15°×2=30°，∠AGD=30°×2=60°， ∴∠BGD=30°+60°=90°， ∴△BGD是等腰直角三角形， ∴BG=DG= ，∴AC=2 ∴AD=2 ，，∴，∴菱形ACEF的面积为： 3==故答案为：12 ．点评：（1）此题主要考查了菱形的性质和应用，要熟练掌握，解答此题的关键是要明确：①菱形具有平行四边形的一切性质；②菱形的四条边都相等； ③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．（2）此题还考查了圆周角定理的应用，要熟练掌握，解答此题的关键是要明确：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．（3）此题还考查了解直角三角形问题，以及勾股定理的应用，要熟练掌握．　18．（3分）（2015•营口）如图，边长为n的正方形OABC的边OA、OC分别在 x轴和y轴的正半轴上，A1、A2、A3、…、An﹣1为OA的n等分点，B1、B2、B3、… Bn﹣1为CB的n等分点，连接A1B1、A2B2、A3B3、…、An﹣1B n﹣1，分别交y= x2（ x≥0）于点C1、C2、C3、…、Cn﹣1，当B25C25=8C25A25时，则n=　5 　．考点：正方形的性质；二次函数图象上点的坐标特征．专题：规律型．分析：根据题意表示出OA25，B25A25的长，由B25C25=8C25A25确定点C25的坐标，代入解析式计算得到答案．解答：解：∵正方形OABC的边长为n，点A1，A2，…，An﹣1为OA的n等分点，点B1，B 2，…，Bn﹣1为CB的n等分点， ∴OA25= ，A25B25=n， ∵B25C25=8C25A25， ∴C25（，）， ∵点C25在y= x2（x≥0）上， ∴ = ×（）2，解得n=5 ．故答案为：5 点评：．本题考查的是二次函数图象上点的特征和正方形的性质，根据正方形的性质表示出点C25的坐标是解题的关键．　三.解答题（19小题10分，20小题10分） 19．（10分）（2015•营口）先化简，再求值： ﹣÷（1﹣ ）．其中m满足一元二次方程m2+（5 tan30°）m﹣12cos60°=0．考点：分式的化简求值；解一元二次方程-因式分解法；特殊角的三角函数值．专题：计算题．分析：原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分后两项通分并利用同分母分式的减法法则计算得到最简结果，求出m 的值代入计算即可求出值．解答：解：原式= ﹣÷=﹣•=﹣== ，方程m2+（5 tan30°）m﹣12cos60°=0，化简得：m2+5m﹣6=0，解得：m=1（舍去）或m=﹣6，当m=﹣6时，原式=﹣ ．点评：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．　20．（10分）（2015•营口）雾霾天气严重影响市民的生活质量．在今年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．（1）本次被调查的市民共有多少人？（2）分别补全条形统计图和扇形统计图，并计算图2中区域B所对应的扇形圆心角的度数；（3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？组别 A百分比 45% m雾霾天气的主要成因工业污染 B汽车尾气排放炉烟气排放 CD15% n其他（滥砍滥伐等）考点：条形统计图；用样本估计总体；扇形统计图．分析：（1）根据条形图和扇形图信息，得到A组人数和所占百分比，求出调查的市民的人数；（2）根据B组人数求出B组百分比，得到D组百分比，根据扇形圆心角的度数= 百分比×360°求出扇形圆心角的度数，根据所求信息补全条形统计图和扇形统计图；（3）根据持有A、B两组主要成因的市民百分比之和求出答案．解答：解：（1）从条形图和扇形图可知，A组人数为90人，占45%， ∴本次被调查的市民共有：90÷45%=200人；（2）60÷200=30%， 30%×360°=108°，区域B所对应的扇形圆心角的度数为：108°， 1﹣45%﹣30%﹣15%=10%， D组人数为：200×10%=20人，（3）100万×（45%+30%）=75万， ∴若该市有100万人口，持有A、B两组主要成因的市民有75万人．点评：本题考查的是条形统计图和扇形统计图的知识，正确获取图中信息并准确进行计算是解题的关键．　四.解答题 21．（12分）（2015•营口）某化妆品专卖店，为了吸引顾客，在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动，凡购物满88元，均可得到一次摇奖的机会．已知在摇奖机内装有2个红球和2个白球，除颜色外其它都相同，摇奖者必须从摇奖机内一次连续摇出两个球，根据球的颜色决定送礼金券的多少（如表）甲种品牌化两白 . 乙种品牌化妆品球两白两红一红两红一红妆品球一白一白礼金券（元 6 12 6礼金券（元 12 612 ））（1）请你用列表法（或画树状图法）求一次连续摇出一红一白两球的概率；（2）如果一个顾客当天在本店购物满88元，若只考虑获得最多的礼品券，请你帮助分析选择购买哪种品牌的化妆品？并说明理由．考点：列表法与树状图法．分析：（1）让所求的情况数除以总情况数即为所求的概率；（2）算出相应的平均收益，比较即可．解答：解：（1）树状图为： ∴一共有6种情况，摇出一红一白的情况共有4种，摇出一红一白的概率= （2）∵两红的概率P= ，两白的概率P= ，一红一白的概率P= ， ∴甲品牌化妆品获礼金券的平均收益是： ×6+ ×12+ ×6=10元．乙品牌化妆品获礼金券的平均收益是： ×12+ ×6+ ×12=8元．；∴我选择甲品牌化妆品．点评：本题主要考查的是概率的计算，画树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．　22．（12分）（2015•营口）如图，我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪，船长马上向我国渔政搜救中心发出求救信号，此时一艘渔政船正巡航到捕鱼船正西方向的B处，该渔政船收到渔政求救中心指令后前去救援，但两船之间有大片暗礁，无法直线到达，于是决定马上调整方向，先向北偏东6 0°方向以每小时30海里的速度航行半小时到达C处，同时捕鱼船低速航行到A点的正北1.5海里D处，渔政船航行到点C处时测得点D在南偏东53°方向上．（1）求CD两点的距离；（2）渔政船决定再次调整航向前去救援，若两船航速不变，并且在点E处相会合，求∠ECD的正弦值．（参考数据：sin53°≈ ，cos53°≈ ，tan53°≈ ）考点：解直角三角形的应用-方向角问题．分析：（1）过点C、D分别作CG⊥AB，DF⊥CG，垂足分别为G，F，根据直角三角形的性质得出CG，再根据三角函数的定义即可得出CD的长；（2）如图，设渔政船调整方向后t小时能与捕渔船相会合，由题意知CE=30t， DE=1.5×2×t=3t，∠EDC=53°，过点E作EH⊥CD于点H，根据三角函数表示出EH ，在Rt△EHC中，根据正弦的定义求值即可．解答：解：（1）过点C、D分别作CH⊥AB，DF⊥CH，垂足分别为H，F， ∵在Rt△CGB中，∠CBG=90°﹣60°=30°， ∴CG= BC= ×（30× ）=7.5， ∵∠DAG=90°， ∴四边形ADFG是矩形， ∴GF=AD=1.5， ∴CF=CG﹣GF=7.5﹣1.5=6，在Rt△CDF中，∠CFD=90°， ∵∠DCF=53°， ∴COS∠DCF= ∴CD= ，= =10（海里）．答：CD两点的距离是10；（2）如图，设渔政船调整方向后t小时能与捕渔船相会合，由题意知CE=30t，DE=1.5×2×t=3t，∠EDC=53°，过点E作EH⊥CD于点H，则∠EHD=∠CHE=90°， ∴sin∠EDH= ，∴EH=EDsin53°=3t× = t， ∴在Rt△EHC中，sin∠ECD= ==．答：sin∠ECD= ．点评：考查了解直角三角形的应用﹣方向角问题，此题是一道方向角问题，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．　23．（12分）（2015•营口）如图，点P是⊙O外一点，PA切⊙O于点A，AB是 ⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD= ，AC=8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．考点：切线的判定；扇形面积的计算．分析：（1）连接OC，证明△PAO≌△PCO，得到∠PCO=∠PAO=90°，证明结论；（2）证明△ADP∽△PDA，得到成比例线段求出BC的长，根据S阴=S⊙O﹣S△ABC 求出答案；（3）连接AE、BE，作BM⊥CE于M，分别求出CM和EM的长，求和得到答案．解答：（1）证明：如图1，连接OC， ∵PA切⊙O于点A，∴∠PAO=90°， ∵BC∥OP， ∴∠AOP=∠OBC，∠COP=∠OCB， ∵OC=OB，∴∠OBC=∠OCB， ∴∠AOP=∠COP，在△PAO和△PCO中，，∴△PAO≌△PCO， ∴∠PCO=∠PAO=90°， ∴PC是⊙O的切线；（2）解：由（1）得PA，PC都为圆的切线， ∴PA=PC，OP平分∠APC，∠ADO=∠PAO=90°， ∴∠PAD+∠DAO=∠DAO+∠AOD， ∴∠PAD=∠AOD， ∴△ADP∽△PDA， ∴，∴AD2=PD•DO， ∵AC=8，PD= ，∴AD= AC=4，OD=3，AO=5，由题意知OD为△的中位线， ∴BC=6，OD=6，AB=10． ∴S阴=S⊙O﹣S△ABC =﹣24；（3）解：如图2，连接AE、BE，作BM⊥CE于M， ∴∠CMB=∠EMB=∠AEB=90°， ∵点E是的中点， ∴∠ECB=∠CBM=∠ABE=45°， CM=MB=3 ，BE=AB•cos45°=5 ∴EM= ，=4 ，则CE=CM+EM=7 ．点评：本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质，灵活运用切线的性质：圆的切线垂直于过切点的半径和切线的判定是解题的关键．　24．（12分）（2015•营口）某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售，已知每天包装大黄米的质量是包装江米质量的倍，且每天包装大黄米和江米的质量之和为45千克．（1）求平均每天包装大黄米和江米的质量各是多少千克？（2）为迎接今年6月20日的“端午节”，该超市决定在前20天增加每天包装大黄米和江米的质量，二者的包装质量与天数的变化情况如图所示，节日后又恢复到原来每天的包装质量．分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式，并写出自变量的取值范围．（3）假设该超市每天都会将当天包装后的大黄米和江米全部售出，已知大黄米成本价为每千克7.9元，江米成本每千克9.5元，二者包装费用平均每千克均为0. 5元，大黄米售价为每千克10元，江米售价为每千克12元，那么在这20天中有哪几天销售大黄米和江米的利润之和大于120元？[总利润=售价额﹣成本﹣包装费用]．考点：一次函数的应用．分析：（1）设平均每天包装大黄米和江米的质量分别为a千克和b千克，然后列方程组求解即可；（2）设出函数的解析式，利用待定系数法求解即可；（3）根据销售大黄米和江米的利润之和大于120元列不等式求解即可．解答：解：（1）设平均每天包装大黄米和江米的质量分别为a千克和b千克，则，解得；答：平均每天包装大黄米和江米的质量分别为25千克和20千克．（2）观察图象，可设平均每天包装大黄米的质量与天数的关系式为y=k1x+b1，平均每天包装江米的质量与天数的关系式为y=k2x+b2． ①当0≤x≤15 时，由y=k1x+b1 的图象过点（0，25），（15，40）．则可列方程组为，解得，∴y1=x+25；由y=k2x+b2 的图象过点（0，20），（15，38）．则可列方程组为，解得，∴；②当15＜x≤20时，由y=k1x+b1 的图象过点（15，40），（20，25）．则可列方程组为，解得，∴y1=﹣3x+85；由y=k2x+b2 的图象过点（15，38），（20，20）．则可列方程组为，解得，∴y2= ，∴，．（3）设第x天销售的总利润为W元， ①当0≤x≤15 时，W=（10﹣7.9﹣0.5）y1+（12﹣9.5﹣0.5）y2=1.6y1+2y2=1.6（x+25）+2（1.2 x+20）=4x+80．由题意4x+80＞120，∴x＞10， ∴x的取值范围为10＜x≤15，由题意知 x=11，12，13，14，15； ②当15＜x≤20 时，W=（10﹣7.9﹣0.5）y1+（12﹣9.5﹣0.5）y2=1.6y1+2y2=1.6（﹣3x+85）+2 （）=﹣12x+30．由题意得：﹣12x+320＞120， ∴x＜，∴x的取值范围为15 由题意知x=16．．答：由①、②可知在第11，12，13，14，15，16天中销售大黄米和江米的总利润大于120元．点评：本题主要考查的是一次函数、二元一次方程组、一元一次不等式的应用，根据图象求得函数的解析式是解题的关键．　25．（14分）（2015•营口）【问题探究】（1）如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD ，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．【深入探究】（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45° ，求BD的长．（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．考点：全等三角形的判定与性质；等腰三角形的性质．分析：（1）首先根据等式的性质证明∠EAC=∠BAD，则根据SAS即可证明△EAC≌△B AD，根据全等三角形的性质即可证明；（2）在△ABC的外部，以A为直角顶点作等腰直角△BAE，使∠BAE=90°，AE= AB，连接EA、EB、EC，证明△EAC≌△BAD，证明BD=CE，然后在直角三角形 BCE中利用勾股定理即可求解；（3）在线段AC的右侧过点A作AE⊥AB于点A，交BC的延长线于点E，证明△E AC≌△BAD，证明BD=CE，即可求解．解答：解：（1）BD=CE．理由是：∵∠BAE=∠CAD， ∴∠BAE+∠BAC=∠CAD+∠BAC，即∠EAC=∠BAD，在△EAC和△BAD中，，∴△EAC≌△BAD， ∴BD=CE；（2）如图2，在△ABC的外部，以A为直角顶点作等腰直角△BAE，使∠BAE=90 °，AE=AB，连接EA、EB、EC． ∵∠ACD=∠ADC=45°， ∴AC=AD，∠CAD=90°， ∴∠BAE+∠BAC=∠CAD+∠BAC，即∠EAC=∠BAD，在△EAC和△BAD中，，∴△EAC≌△BAD， ∴BD=CE． ∵AE=AB=7， ∴BE= =7 ，∠AEC=∠AEB=45°，又∵∠ABC=45°， ∴∠ABC+∠ABE=45°+45°=90°， ∴EC= ==，∴BD=CE= ．（3）如图3，在线段AC的右侧过点A作AE⊥AB于点A，交BC的延长线于点E，连接BE． ∵AE⊥AB， ∴∠BAE=90°，又∵∠ABC=45°， ∴∠E=∠ABC=45°， ∴AE=AB=7，BE= =7 ，又∵∠ACD=∠ADC=45°， ∴∠BAE=∠DAC=90°， ∴∠BAE﹣∠BAC=∠DAC﹣∠BAC，即∠EAC=∠BAD，在△EAC和△BAD中，，∴△EAC≌△BAD， ∴BD=CE， ∵BC=3， ∴BD=CE=7 ﹣3（cm）．点评：本题考查了全等三角形的判定与性质，正确理解三个题目之间的联系，构造（1 ）中的全等三角形是解决本题的关键．　26．（14分）（2015•营口）如图1，一条抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，且当x=﹣1和x=3时，y的值相等，直线y= x﹣ 与抛物线有两个交点，其中一个交点的横坐标是6，另一个交点是这条抛物线的顶点M．（1）求这条抛物线的表达式．（2）动点P从原点O出发，在线段OB上以每秒1个单位长度的速度向点B运动，同时点Q从点B出发，在线段BC上以每秒2个单位长度的速度向点C运动，当一个点到达终点时，另一个点立即停止运动，设运动时间为t秒． ①若使△BPQ为直角三角形，请求出所有符合条件的t值； ②求t为何值时，四边形ACQP的面积有最小值，最小值是多少？（3）如图2，当动点P运动到OB的中点时，过点P作PD⊥x轴，交抛物线于点D ，连接OD，OM，MD得△ODM，将△OPD沿x轴向左平移m个单位长度（0＜m ＜2），将平移后的三角形与△ODM重叠部分的面积记为S，求S与m的函数关系式．考点：二次函数综合题．分析：（1）因为当x=﹣1和x=3时，y的值相等，所以抛物线的对称轴为直线x=1，将x =1和x=6分别代入中，可求得抛物线的顶点坐标和与直线另一交点的坐标，然后设出抛物线的顶点式，最后将（6，6）代入即可求得抛物线的解析式；（2）①先求得A（ 2，0），B（4，0），C（0，﹣3），从而可得到OA=2，OB=4；OC=3，由勾股定理知BC=5，有∠PQB=90°或∠BPQ=90°两种情况：当∠PQB=90°时，可得△P QB∽△COB，当∠BPQ=90°时，可得△BPQ∽△BOC；②过点Q作QG⊥AB于G，能够等到△BGQ∽△BOC，可求得GQ= 然后S四边形ACQP=S△ABC﹣S△BPQ=9 ，从而可求得四边形的面积的最值；（3）先求得点D的坐标，然后根据平移与坐标变换的关系得出点P1（2﹣m，0 ），D1（2﹣m，﹣3），E（2﹣m，﹣3+ ），①当0 时，作FH⊥轴于点H，S四边形ACQP=S△ABC﹣S△BPQ；当时，设D1P1交OM于点F，S△OEF= =．解答：解：（1）∵当x=﹣1和x=3时，y的值相等， ∴抛物线的对称轴为直线x=1，把x=1和x=6分别代入中，得顶点M（ 1，﹣ ），另一个交点坐标为（6，6），则可设抛物线的表达式为y=a（x﹣1）2﹣ ，将（6，6）代入其中，解得a= ， ∴抛物线的表达式为y= （2）如下图：，即 y= …3分当y=0时，．解得：x1=﹣2，x2=4．由题意可知：A（ 2，0），B（4，0），所以OA=2，OB=4；当x=0时，y=﹣3，所以点C（0，﹣3），OC=3，由勾股定理知BC=5， OP=1×t=t，BQ=2×t=2t， ①∵∠PBQ是锐角， ∴有∠PQB=90°或∠BPQ=90°两种情况：当∠PQB=90°时，可得△PQB∽△COB， ∴，∴，∴t= ；当∠BPQ=90°时，可得△BPQ∽△BOC， ∴，∴，∴t= ；由题意知0≤t≤2.5， ∴当t= 或t= 时，以B，P，Q为顶点的三角形是直角三角形…7分 ②过点Q作QG⊥AB于G， ∴△BGQ∽△BOC， ∴，，∴∴GQ= ，∴S四边形ACQP=S△ABC﹣S△BPQ =﹣==9 ．∵ ＞0， ∴四边形ACQP的面积有最小值，又∵t=2 满足0≤t≤2.5， ∴当t=2时，四边形ACQP的面积最小，最小值是（3）如下图，；由OB=4得OP=2，把 x=2代入y= 所以D（2，﹣3），中，得y=﹣3，直线CD∥x轴，设直线OD的解析式为y=k1x，则k1= ，所以y=﹣ x，因为△P1O1D1是由△POD 沿x轴向左平移m个单位得到的，所以P1（2﹣m，0），D1（2﹣m，﹣3），E（2﹣m ，﹣3+ ）设直线OM的解析式为y=k2x，则k2= ，所以y=﹣ ①当0 ．时，作FH⊥轴于点H，由题意O1（﹣m，0），又∵O1D1∥OD， ∴直线O1D1的解析式为y=﹣ ．联立方程组，解得，所以F（所以FH= ，），，=﹣﹣==3m﹣ ．如下图，当时，设D1P1交OM于点F，直线OM的解析式为y=﹣ ，所以F（2﹣m，﹣ 所以EF= ），，∴S△OEF= =综上所述，S= 点评：．本题主要考查的是二次函数的综合应用，属于动点问题，题目涉及了求二次函数的解析式，二次函数的最值，相似三角形的性质和判定、求不规则图形的面积等知识，难度较大．