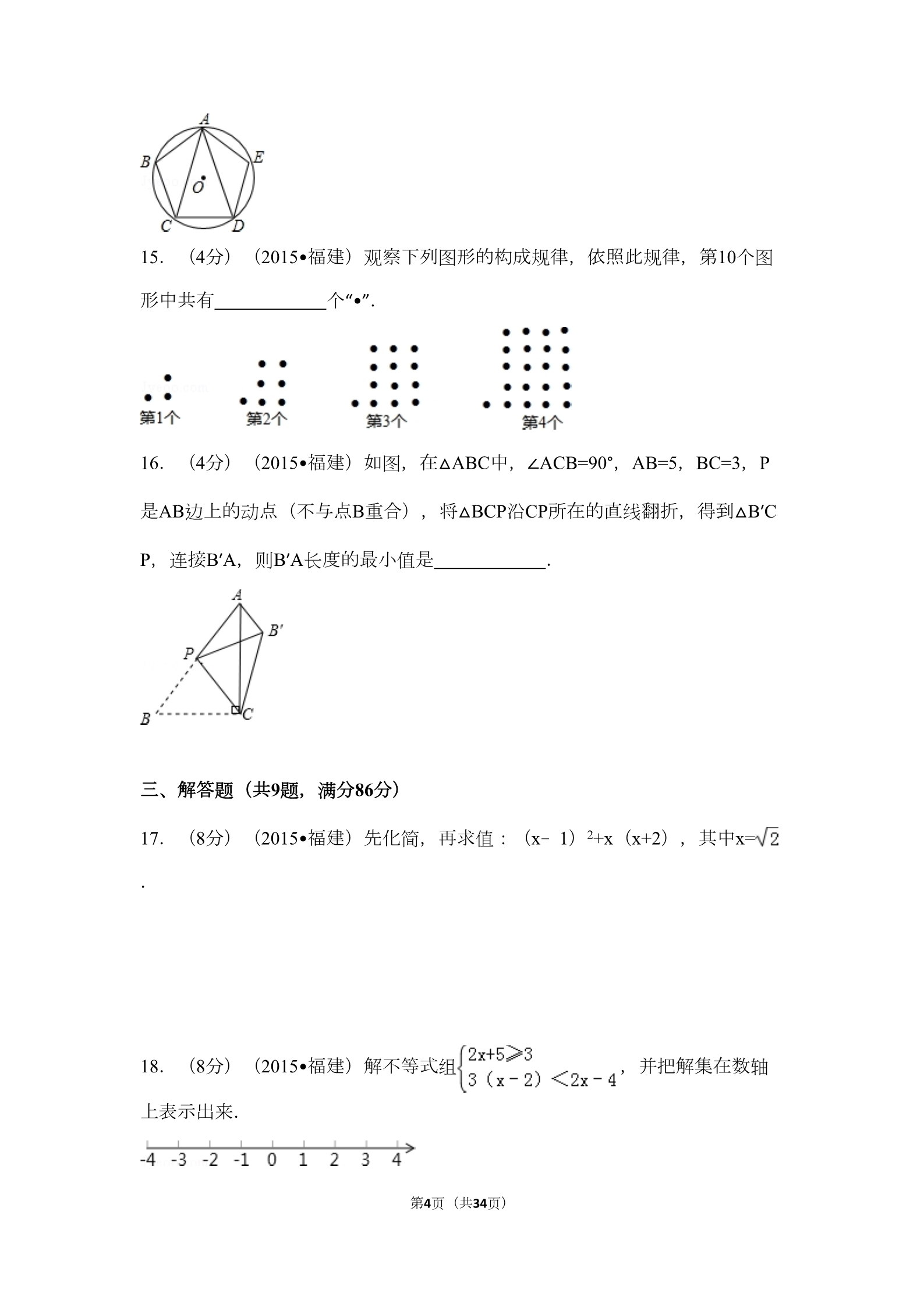
2015年福建省三明市中考数学试卷（含解析版）

2015年福建省三明市中考数学试卷一、选择题（共10题，每题4分，满分40分，每题只有一个正确选项） 1．（4分）（2015•福建）下列各数中，绝对值最大的数是（　　） ﹣3 ﹣2 　A 5 BC 0 D．．．．2．（4分）（2015•福建）一个正常人的心跳平均每分70次，一天大约跳100800 次，将100800用科学记数法表示为（　　） 0.1008×106 1.008×106 1.008×105 10.08×104 　A BCD．．．．3．（4分）（2015•福建）如图是由4个完全相同的小正方形组成的几何体，这个几何体的主视图是（　　）　 A． B． C． D． 4．（4分）（2015•福建）下列计算正确的是（　　） 2﹣1=﹣2 　A 22=4 B 20=0 CD=±2 ．．．．5．（4分）（2015•福建）在九（1）班的一次体育测试中，某小组7位女生的一分钟跳绳次数分别是：162，167，158，165，175，142，167，这组数据的中位数是（　　）　A 156 B 162 C 165 D 167 ．．．．6．（4分）（2015•福建）如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（　　）第1页（共34页） AB∥CD 　A B AB=CD C AC=BD D OA=OC ．．．．7．（4分）（2015•福建）在一个不透明的盒子里装有3个黑球和1个白球，每个球除颜色外都相同，从中任意摸出2个球，下列事件中，不可能事件是（　　）　A 摸出的2个球都是白球 B 摸出的2个球有一个是白球．．　C 摸出的2个球都是黑球 D 摸出的2个球有一个黑球．．8．（4分）（2015•福建）在半径为6的⊙O中，60°圆心角所对的弧长是（　　）π2π 4π 6π 　A BCD．．．．9．（4分）（2015•福建）如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于 AB）为半径作弧，两弧相交于点M和N，作直线MN交 AB于点D，交BC于点E，连接CD，下列结论错误的是（　　） ∠A=∠BED ∠ECD=∠EDC 　A AD=BD B BD=CD CD．．．．10．（4分）（2015•福建）如图，已知点A是双曲线y= 在第一象限的分支上的一个动点，连接AO并延长交另一分支于点B，过点A作y轴的垂线，过点B作x轴第2页（共34页）的垂线，两垂线交于点C，随着点A的运动，点C的位置也随之变化．设点C的坐标为（m，n），则m，n满足的关系式为（　　） n=﹣2m n=﹣4m 　A ．　BCDn=﹣ n=﹣ ．．．二、填空题（共6题，每题4分，满分24分） 11．（4分）（2015•福建）化简： =　　　　　　． 12．（4分）（2015•福建）某班数学老师想了解学生对数学的喜欢程度，对全班50名学生进行调查，根据调查结果绘制了扇形统计图（如图所示），其中A 表示“很喜欢”，B表示“一般”，C表示“不喜欢”，则该班“很喜欢”数学的学生有　　　　　　人． 13．（4分）（2015•福建）在一次函数y=kx+3中，y的值随着x值的增大而增大，请你写出符合条件的k的一个值：　　　　　　． 14．（4分）（2015•福建）如图，正五边形ABCDE内接于⊙O，则∠CAD=　　　　　　度．第3页（共34页） 15．（4分）（2015•福建）观察下列图形的构成规律，依照此规律，第10个图形中共有　　　　　　个“•”． 16．（4分）（2015•福建）如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P 是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′C P，连接B′A，则B′A长度的最小值是　　　　　　．　三、解答题（共9题，满分86分） 17．（8分）（2015•福建）先化简，再求值：（x﹣1）2+x（x+2），其中x= ．　18．（8分）（2015•福建）解不等式组，并把解集在数轴上表示出来．第4页（共34页）　19．（8分）（2015•福建）如图，一条河的两岸l1，l2互相平行，在一次综合实践活动中，小颖去测量这条河的宽度，先在对岸l1上选取一个点A，然后在河岸 l2时选择点B，使得AB与河岸垂直，接着沿河岸l2走到点C处，测得BC=60米，∠ BCA=62°，请你帮小颖算出河宽AB（结果精确到1米）．（参考数据：sin62°≈0. 88，cos62°≈0.47，tan62°≈1.88）　20．（8分）（2015•福建）某校开展校园“美德少年”评选活动，共有“助人为乐 ”，“自强自立”、“孝老爱亲”，“诚实守信”四种类别，每位同学只能参评其中一类，评选后，把最终入选的20位校园“美德少年”分类统计，制作了如下统计表，后来发现，统计表中前两行的数据都是正确的，后两行的数据中有一个是错误的．类别频数频率 a0.20 助人为乐美德少年自强自立美德少年孝老爱亲美德少年诚实守信美德少年 376b0.35 0.32 根据以上信息，解答下列问题：第5页（共34页）（1）统计表中的a=　　　　　　，b　　　　　　；（2）统计表后两行错误的数据是　　　　　　，该数据的正确值是　　　　　　；（3）校园小记者决定从A，B，C三位“自强自立美德少年”中随机采访两位，用画树状图或列表的方法，求A，B都被采访到的概率．　21．（8分）（2015•福建）某一天，蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子，到菜市场去卖，黄瓜和茄子当天的批发价与零售价如下表所示：品名黄瓜茄子 34批发价（元/千克）零售价（元/千克） 47当天他卖完这些黄瓜和茄子共赚了90元，这天他批发的黄瓜和茄子分别是多少千克？　22．（10分）（2015•福建）已知二次函数y=﹣x2+2x+m．（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；（2）如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．第6页（共34页）　23．（10分）（2015•福建）已知：AB是⊙O的直径，点P在线段AB的延长线上，BP=OB=2，点Q在⊙O上，连接PQ．（1）如图①，线段PQ所在的直线与⊙O相切，求线段PQ的长；（2）如图②，线段PQ与⊙O还有一个公共点C，且PC=CQ，连接OQ，AC交于点D． ①判断OQ与AC的位置关系，并说明理由； ②求线段PQ的长．　24．（12分）（2015•福建）如图，在平面直角坐标系中，顶点为A（1，﹣1）的抛物线经过点B（5，3），且与x轴交于C，D两点（点C在点D的左侧）．（1）求抛物线的解析式；第7页（共34页）（2）求点O到直线AB的距离；（3）点M在第二象限内的抛物线上，点N在x轴上，且∠MND=∠OAB，当△DM N与△OAB相似时，请你直接写出点M的坐标．　25．（14分）（2015•福建）在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG ≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2= ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．　　第8页（共34页） 2015年福建省三明市中考数学试卷参考答案与试题解析一、选择题（共10题，每题4分，满分40分，每题只有一个正确选项） 1．（4分）（2015•福建）下列各数中，绝对值最大的数是（　　） ﹣3 ﹣2 　A 5 BC 0 D．．．．考点：有理数大小比较；绝对值．菁优网版权所有分析：根据绝对值的概念，可得出距离原点越远，绝对值越大，可直接得出答案．解答：解：|5|=5，|﹣3|=3，|0|=0，|﹣2|=2， ∵5＞3＞2＞0， ∴绝对值最大的数是5，故选：A．点评：本题考查了实数的大小比较，以及绝对值的概念，解决本题的关键是求出各数的绝对值．　2．（4分）（2015•福建）一个正常人的心跳平均每分70次，一天大约跳100800 次，将100800用科学记数法表示为（　　） 0.1008×106 1.008×106 1.008×105 10.08×104 　A BCD．．．．考点：科学记数法—表示较大的数．菁优网版权所有分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时第9页（共34页），要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：100800=1.008×105．故故选C．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中 1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　3．（4分）（2015•福建）如图是由4个完全相同的小正方形组成的几何体，这个几何体的主视图是（　　） A． B． C． D．考点：简单组合体的三视图．菁优网版权所有分析：主视图是从正面看到的图形，是这个几何体从正面照射的正投影，据此求解．解答：解：观察该几何体发现：其主视图的第一层有两个正方形，上面有一个正方形，且位于左侧，故选D．点评：本题考查了简单组合体的三视图，解题的关键是了解主视图的定义，难度不大．　第10页（共34页） 4．（4分）（2015•福建）下列计算正确的是（　　） 2﹣1=﹣2 　A 22=4 B 20=0 CD=±2 ．．．．考点：负整数指数幂；有理数的乘方；算术平方根；零指数幂．菁优网版权所分析： A：根据有理数的乘方的运算方法判断即可． B：根据零指数幂的运算方法判断即可． C：根据负整数指数幂的运算方法判断即可． D：根据算术平方根的含义和求法判断即可．解答：解：∵22=4， ∴选项A正确； ∵20=1， ∴选项B不正确； ∵2﹣1= ， ∴选项C不正确； ∵，∴选项D不正确．故选：A．点评：（1）此题主要考查了负整数指数幂的运算，要熟练掌握，解答此题的关键是要明确：①a﹣p= （a≠0，p为正整数）；②计算负整数指数幂时，一定要根据负整数指数幂的意义计算；③当底数是分数时，只要把分子、分母颠倒，负指数就可变为正指数．（2）此题还考查了零指数幂的运算，要熟练掌握，解答此题的关键是要明确： ①a0=1（a≠0）；②00≠1．第11页（共34页）（3）此题还考查了有理数的乘方的运算方法，以及算术平方根的含义和求法，要熟练掌握．　5．（4分）（2015•福建）在九（1）班的一次体育测试中，某小组7位女生的一分钟跳绳次数分别是：162，167，158，165，175，142，167，这组数据的中位数是（　　）　A 156 B 162 C 165 D 167 ．．．．考点：中位数．菁优网版权所有分析：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．解答：解：这组数据按照从小到大的顺序排列为：142，158，162，165，167，167，1 75，第四个数为165，则中位数为：165．故选C．点评：本题考查了中位数的知识，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．　第12页（共34页） 6．（4分）（2015•福建）如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（　　） AB∥CD 　A B AB=CD C AC=BD D OA=OC ．．．．考点：平行四边形的性质．菁优网版权所有分析：根据平行四边形的性质推出即可．解答：解：∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD，OA=OC，但是AC和BD不一定相等，故选C．点评：本题考查了平行四边形的性质的应用，能熟记平行四边形的性质是解此题的关键，注意：平行四边形的对边相等且平行，平行四边形的对角线互相平分．　7．（4分）（2015•福建）在一个不透明的盒子里装有3个黑球和1个白球，每个球除颜色外都相同，从中任意摸出2个球，下列事件中，不可能事件是（　　）　A 摸出的2个球都是白球 B 摸出的2个球有一个是白球．．　C 摸出的2个球都是黑球 D 摸出的2个球有一个黑球．．考点：随机事件．菁优网版权所有分析：根据必然事件、不可能事件、随机事件的概念可区别各类事件．第13页（共34页）解答：解：A、只有一个白球，故A是不可能事件，故A正确； B、摸出的2个球有一个是白球是随机事件，故B错误； C、摸出的2个球都是黑球是随机事件，故C错误； D、摸出的2个球有一个黑球是随机事件，故D错误；故选：A．点评：本题考查了可能性的大小，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．　8．（4分）（2015•福建）在半径为6的⊙O中，60°圆心角所对的弧长是（　　）π2π 4π 6π 　A BCD．．．．考点：弧长的计算．菁优网版权所有分析：根据弧长的计算公式l= 计算即可． =2π．解答：解：l= 故选：B．点评： =本题考查的是弧长的计算，掌握弧长的计算公式：l= 是解题的关键．　第14页（共34页） 9．（4分）（2015•福建）如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于 AB）为半径作弧，两弧相交于点M和N，作直线MN交 AB于点D，交BC于点E，连接CD，下列结论错误的是（　　） ∠A=∠BED ∠ECD=∠EDC 　A AD=BD B BD=CD CD．．．．考点：作图— 基本作图；线段垂直平分线的性质；直角三角形斜边上的中线．版分析：由题意可知：MN为AB的垂直平分线，可以得出AD=BD；CD为直角三角形AB C斜边上的中线，得出CD=BD；利用三角形的内角和得出∠A=∠BED；因为∠A≠ 60°，得不出AC=AD，无法得出EC=ED，则∠ECD=∠EDC不成立；由此选择答案即可．解答：解：∵MN为AB的垂直平分线， ∴AD=BD，∠BDE=90°； ∵∠ACB=90°， ∴CD=BD； ∵∠A+∠B=∠B+∠BED=90°， ∴∠A=∠BED； ∵∠A≠60°，AC≠AD， ∴EC≠ED， ∴∠ECD≠∠EDC．故选：D．第15页（共34页）点评：此题考查了线段垂直平分线的性质以及直角三角形的性质．注意垂直平分线上任意一点，到线段两端点的距离相等．　10．（4分）（2015•福建）如图，已知点A是双曲线y= 在第一象限的分支上的一个动点，连接AO并延长交另一分支于点B，过点A作y轴的垂线，过点B作x轴的垂线，两垂线交于点C，随着点A的运动，点C的位置也随之变化．设点C的坐标为（m，n），则m，n满足的关系式为（　　） n=﹣2m n=﹣4m 　A BCDn=﹣ n=﹣ ．．．．考点：反比例函数图象上点的坐标特征．菁优网版权所有分析：首先根据点C的坐标为（m，n），分别求出点A的坐标、点B的坐标；然后根据 AO、BO所在的直线的斜率相同，求出m，n满足的关系式即可．解答：解：∵点C的坐标为（m，n）， ∴点A的纵坐标是n，横坐标是：， ∴点A的坐标为（，n）， ∵点C的坐标为（m，n）， ∴点B的横坐标是m，纵坐标是：，第16页（共34页） ∴点B的坐标为（m，），又∵ ，∴mn= ∴m2n2=4，又∵m＜0，n＞0， ∴mn=﹣2， ∴n=﹣ 故选：B．点评：此题主要考查了反比例函数的图象上点的坐标的特征，要熟练掌握，解答此题的关键是要明确：①图象上的点（x，y）的横纵坐标的积是定值k，即xy=k； ②双曲线是关于原点对称的，两个分支上的点也是关于原点对称；③在xk图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．　二、填空题（共6题，每题4分，满分24分） 11．（4分）（2015•福建）化简：考点：约分．菁优网版权所有 =　　．分析：将分母分解因式，然后再约分、化简．解答：解：原式= =．点评：利用分式的性质变形时必须注意所乘的（或所除的）整式不为零．第17页（共34页） 12．（4分）（2015•福建）某班数学老师想了解学生对数学的喜欢程度，对全班50名学生进行调查，根据调查结果绘制了扇形统计图（如图所示），其中A 表示“很喜欢”，B表示“一般”，C表示“不喜欢”，则该班“很喜欢”数学的学生有　 18　人．考点：扇形统计图．菁优网版权所有专题：计算题．分析：根据扇形统计图求出A占的百分比，由调查的总人数50计算即可得到结果．解答：解：根据题意得：（1﹣16%﹣48%）×50=18（人），则该班“很喜欢”数学的学生有18人．故答案为：18 点评：此题考查了扇形统计图，弄清图形中的数据是解本题的关键．　13．（4分）（2015•福建）在一次函数y=kx+3中，y的值随着x值的增大而增大，请你写出符合条件的k的一个值：　2　．考点：一次函数的性质．菁优网版权所有专题：开放型．分析：直接根据一次函数的性质进行解答即可．第18页（共34页）解答：解：当在一次函数y=kx+3中，y的值随着x值的增大而增大时，k＞0，则符合条件的k的值可以是1，2，3，4，5… 故答案是：2．点评：本题考查了一次函数的性质．在直线y=kx+b中，当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小．　14．（4分）（2015•福建）如图，正五边形ABCDE内接于⊙O，则∠CAD=　36　度．考点：圆周角定理；正多边形和圆．菁优网版权所有分析：圆内接正五边形ABCDE的顶点把圆五等分，即可求得五条弧的度数，根据圆周角的度数等于所对的弧的度数的一半即可求解．解答：解：∵五边形ABCDE是正五边形， ∴=====72°， ∴∠ADB= ×72°=36°．故答案为36．点评：本题考查了正多边形的计算，理解正五边形的顶点是圆的五等分点是关键．　第19页（共34页） 15．（4分）（2015•福建）观察下列图形的构成规律，依照此规律，第10个图形中共有　111　个“•”．考点：规律型：图形的变化类．菁优网版权所有分析：观察图形可知前4个图形中分别有：3，7，13，21个“•”，所以可得规律为：第n 个图形中共有[n（n+1）+1]个“•”．再将n=10代入计算即可．解答：解：由图形可知： n=1时，“•”的个数为：1×2+1=3， n=2时，“•”的个数为：2×3+1=7， n=3时，“•”的个数为：3×4+1=13， n=4时，“•”的个数为：4×5+1=21，所以n=n时，“•”的个数为：n（n+1）+1， n=10时，“•”的个数为：10×11+1=111．故答案为111．点评：本题主要考查了规律型：图形的变化类，关键在观察、分析已知数据，寻找它们之间的相互联系，探寻其规律，难度适中．　第20页（共34页） 16．（4分）（2015•福建）如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P 是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′C P，连接B′A，则B′A长度的最小值是　1　．考点：翻折变换（折叠问题）．菁优网版权所有分析：首先由勾股定理求得AC的长度，由轴对称的性质可知BC=CB′=3，当B′A有最小值时，即AB′+CB′有最小值，由两点之间线段最短可知当A、B′、C三点在一条直线上时，AB′有最小值．解答：解：在Rt△ABC中，由勾股定理可知：AC= 由轴对称的性质可知：BC=CB′=3， ∵CB′长度固定不变， ==4， ∴当AB′+CB′有最小值时，AB′的长度有最小值．根据两点之间线段最短可知：A、B′、C三点在一条直线上时，AB′有最小值， ∴AB′=AC﹣B′C=4﹣3=1．故答案为：1．点评：本题主要考查的是轴对称的性质、勾股定理和线段的性质，将求B′A的最小值转化为求AB′+CB′的最小值是解题的关键．　三、解答题（共9题，满分86分）第21页（共34页） 17．（8分）（2015•福建）先化简，再求值：（x﹣1）2+x（x+2），其中x= ．考点：整式的混合运算—化简求值．菁优网版权所有分析：原式第一项利用完全平方公式化简，第二项利用单项式乘多项式法则计算，去括号合并得到最简结果，将x的值代入计算即可求出值．解答：解：原式=x2﹣2x+1+x2+2x=2×2+1，当x= 时，原式=4+1=5．点评：此题考查了整式的混合运算﹣化简求值，涉及的知识有：完全平方公式，平方差公式，多项式除单项式，去括号法则，以及合并同类项法则，熟练掌握公式及法则是解本题的关键．　18．（8分）（2015•福建）解不等式组，并把解集在数轴上表示出来．考点：解一元一次不等式组；在数轴上表示不等式的解集．菁优网版权所有分析：先求出不等式组中每一个不等式的解集，然后把不等式的解集表示在数轴上，再表示出它们的公共部分即可．解答：解：，解①得：x≥﹣1，解②得：x＜2．第22页（共34页），不等式组的解集是：﹣1≤x＜2．点评：本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．要注意x是否取得到，若取得到则x在该点是实心的．反之x在该点是空心的．　19．（8分）（2015•福建）如图，一条河的两岸l1，l2互相平行，在一次综合实践活动中，小颖去测量这条河的宽度，先在对岸l1上选取一个点A，然后在河岸 l2时选择点B，使得AB与河岸垂直，接着沿河岸l2走到点C处，测得BC=60米，∠ BCA=62°，请你帮小颖算出河宽AB（结果精确到1米）．（参考数据：sin62°≈0. 88，cos62°≈0.47，tan62°≈1.88）考点：解直角三角形的应用．菁优网版权所有专题：应用题．分析：在直角三角形ABC中，利用锐角三角函数定义求出AB的长即可．解答：解：在Rt△ABC中，BC=60米，∠BCA=62°，可得tan∠BCA= ，即AB=BC•tan∠BCA=60×1.88≈113（米），则河宽AB为113米．点评：此题考查了解直角三角形的应用，熟练掌握锐角三角函数定义是解本题的关键．第23页（共34页）　20．（8分）（2015•福建）某校开展校园“美德少年”评选活动，共有“助人为乐 ”，“自强自立”、“孝老爱亲”，“诚实守信”四种类别，每位同学只能参评其中一类，评选后，把最终入选的20位校园“美德少年”分类统计，制作了如下统计表，后来发现，统计表中前两行的数据都是正确的，后两行的数据中有一个是错误的．类别频数频率 a0.20 助人为乐美德少年自强自立美德少年孝老爱亲美德少年诚实守信美德少年 376b0.35 0.32 根据以上信息，解答下列问题：（1）统计表中的a=　4　，b　0.15　；（2）统计表后两行错误的数据是　0.32　，该数据的正确值是　0.30　；（3）校园小记者决定从A，B，C三位“自强自立美德少年”中随机采访两位，用画树状图或列表的方法，求A，B都被采访到的概率．考点：列表法与树状图法；频数（率）分布表．菁优网版权所有分析：（1）根据频率= 直接求得a、b的值即可；（2）用频数除以样本总数看是否等于已知的频率即可；（3）列表将所有等可能的结果列举出来，利用概率公式求解即可．解答：解：（1）由题意得：a=20×0.20=4，b=3÷20=0.15；（2）∵6÷20=0.3≠0.32， ∴最后一行数据错误，正确的值为0.30；第24页（共34页）（3）列表得： A B C A ABAC B BABC C CA CB ∵共有6种等可能的结果，A、B都被选中的情况有2种， ∴P（A，B都被采访到）= = ．点评：本题考查了频数分布表及列表或树形图求概率的知识，解题的关键是能够正确的列表将所有等可能的结果列举出来，难度不大．　21．（8分）（2015•福建）某一天，蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子，到菜市场去卖，黄瓜和茄子当天的批发价与零售价如下表所示：品名黄瓜茄子 34批发价（元/千克）零售价（元/千克） 47当天他卖完这些黄瓜和茄子共赚了90元，这天他批发的黄瓜和茄子分别是多少千克？考点：二元一次方程组的应用．菁优网版权所有分析：设批发的黄瓜是x千克，茄子是y千克，根据“用了145元从蔬菜批发市场批发一些黄瓜和茄子，卖完这些黄瓜和茄子共赚了90元，”列出方程组解答即可．解答：解：设批发的黄瓜是x千克，茄子是y千克，由题意得第25页（共34页）解得答：这天他批发的黄瓜15千克，茄子是25千克．点评：此题考查二元一次方程组的实际运用，找出题目蕴含的数量关系是解决问题的关键．　22．（10分）（2015•福建）已知二次函数y=﹣x2+2x+m．（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；（2）如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．考点：抛物线与x轴的交点；二次函数的性质．菁优网版权所有分析：（1）由二次函数的图象与x轴有两个交点，得到△=22+4m＞0于是得到m＞﹣1 ；（2）把点A（3，0）代入二次函数的解析式得到m=3，于是确定二次函数的解析式为：y=﹣x2+2x+3，求得B（0，3），得到直线AB的解析式为：y=﹣x+3，把对称轴方程x=1，直线y=﹣x+3即可得到结果．第26页（共34页）解答：解：（1）∵二次函数的图象与x轴有两个交点， ∴△=22+4m＞0 ∴m＞﹣1；（2）∵二次函数的图象过点A（3，0）， ∴0=﹣9+6+m ∴m=3， ∴二次函数的解析式为：y=﹣x2+2x+3，令x=0，则y=3， ∴B（0，3），设直线AB的解析式为：y=kx+b， ∴，解得：，∴直线AB的解析式为：y=﹣x+3， ∵抛物线y=﹣x2+2x+3，的对称轴为：x=1， ∴把x=1代入y=﹣x+3得y=2， ∴P（1，2）．点评：本题考查了二次函数与x轴的交点问题，求函数的解析式，知道抛物线的对称轴与直线AB的交点即为点P的坐标是解题的关键．　23．（10分）（2015•福建）已知：AB是⊙O的直径，点P在线段AB的延长线上，BP=OB=2，点Q在⊙O上，连接PQ．（1）如图①，线段PQ所在的直线与⊙O相切，求线段PQ的长；第27页（共34页）（2）如图②，线段PQ与⊙O还有一个公共点C，且PC=CQ，连接OQ，AC交于点D． ①判断OQ与AC的位置关系，并说明理由； ②求线段PQ的长．考点：圆的综合题．菁优网版权所有分析：（1）如图①，连接OQ．利用切线的性质和勾股定理来求PQ的长度．（2）如图②，连接BC．利用三角形中位线的判定与性质得到BC∥OQ．根据圆周角定理推知BC⊥AC，所以，OQ⊥AC．（3）利用割线定理来求PQ的长度即可．解答：解：（1）如图①，连接OQ． ∵线段PQ所在的直线与⊙O相切，点Q在⊙O上， ∴OQ⊥OP．又∵BP=OB=OQ=2， ∴PQ= ==2 ，即PQ=2 ；（2）OQ⊥AC．理由如下：如图②，连接BC． ∵BP=OB， ∴点B是OP的中点，又∵PC=CQ， ∴点C是PQ的中点，第28页（共34页） ∴BC是△PQO的中位线， ∴BC∥OQ．又∵AB是直径， ∴∠ACB=90°，即BC⊥AC， ∴OQ⊥AC．（3）如图②，PC•PQ=PB•PA，即 PQ2=2×6，解得PQ=2 ．点评：本题考查了圆的综合题．掌握圆周角定理，三角形中位线定理，平行线的性质，熟练利用割线定理进行几何计算．　24．（12分）（2015•福建）如图，在平面直角坐标系中，顶点为A（1，﹣1）的抛物线经过点B（5，3），且与x轴交于C，D两点（点C在点D的左侧）．（1）求抛物线的解析式；（2）求点O到直线AB的距离；第29页（共34页）（3）点M在第二象限内的抛物线上，点N在x轴上，且∠MND=∠OAB，当△DM N与△OAB相似时，请你直接写出点M的坐标．考点：二次函数综合题．菁优网版权所有分析：（1）根据待定系数法，可得抛物线的解析式；（2）根据勾股定理，可得OA2、OB2、AB2的长，根据勾股定理的逆定理，可得∠OAB的度数，根据点到直线的距离的定义，可得答案；（3）根据抛物线上的点满足函数解析式，可得方程②，根据相似三角形的性质，可得方程①③，根据解方程组，可得M点的坐标．解答：解：（1）设抛物线的解析式为y=a（x﹣1）2﹣1，将B点坐标代入函数解析式，得（5﹣1）2a﹣1=3，解得a= ．故抛物线的解析式为y= （x﹣1）2﹣1；（2）由勾股定理，得OA2=11+12=2，OB2=52+32=34，AB2=（5﹣1）2+（3+1）2 =32， OA2+AB2=OB2， ∴∠OAB=90°， O到直线AB的距离是OA= ；（3）设M（a，b），N（a，0）第30页（共34页）当y=0时，（x﹣1）2﹣1=0，解得x1=3，x2=﹣1， D（3，0），DN=3﹣a． ①当△MND∽△OAB时，化简，得4b=a﹣3 ① =，即 =，M在抛物线上，得b= （a﹣1）2﹣1 ② 联立①②，得，解得a1=3（不符合题意，舍），a2=﹣2，b= ， M1（﹣2，），当△MND∽△BAO时， =，即 =，化简，得b=12﹣4a ③，联立②③，得，解得a1=3（不符合题意，舍），a2=﹣17，b=12﹣4×（﹣17）=80， M2（﹣17，80）．综上所述：当△DMN与△OAB相似时，点M的坐标（﹣2，），（﹣17，80）．点评：本题考查了二次函数综合题，（1）设成顶点式的解析式是解题关键，（2）利用了勾股定理及勾股定理的逆定理，点到直线的距离；（3）利用了相似三角形的性质，图象上的点满足函数解析式得出方程组是解题关键，要分类讨论，以防遗漏．第31页（共34页）　25．（14分）（2015•福建）在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG ≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2= ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．考点：四边形综合题．菁优网版权所有分析：（1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF ；（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AE G≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出 CE=CF，BE=BM，NF= DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG2=ME2+MG2，等量代换即可证明EF2=ME2+NF2；（3）将△ADF绕着点A顺时针旋转90°，得到△ABG，根据旋转的性质可以得到 △ADF≌△ABG，则DF=BG，再证明△AEG≌△AEF，得出EG=EF，由EG=BG+B E，等量代换得到EF=BE+DF．第32页（共34页）解答：（1）证明：∵△ADF绕着点A顺时针旋转90°，得到△ABG， ∴AF=AG，∠FAG=90°， ∵∠EAF=45°， ∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）证明：设正方形ABCD的边长为a．将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF， ∴EG=EF． ∵∠CEF=45°， ∴△BME、△DNF、△CEF均为等腰直角三角形， ∴CE=CF，BE=BM，NF= DF， ∴a﹣BE=a﹣DF， ∴BE=DF， ∴BE=BM=DF=BG， ∴∠BMG=45°， ∴∠GME=45°+45°=90°， ∴EG2=ME2+MG2， ∵EG=EF，MG= BM= DF=NF， ∴EF2=ME2+NF2；（3）解：EF2=2BE2+2DF2．第33页（共34页）点评：本题是四边形综合题，其中涉及到正方形的性质，旋转的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，矩形的性质，勾股定理．准确作出辅助线利用数形结合及类比思想是解题的关键．　第34页（共34页）