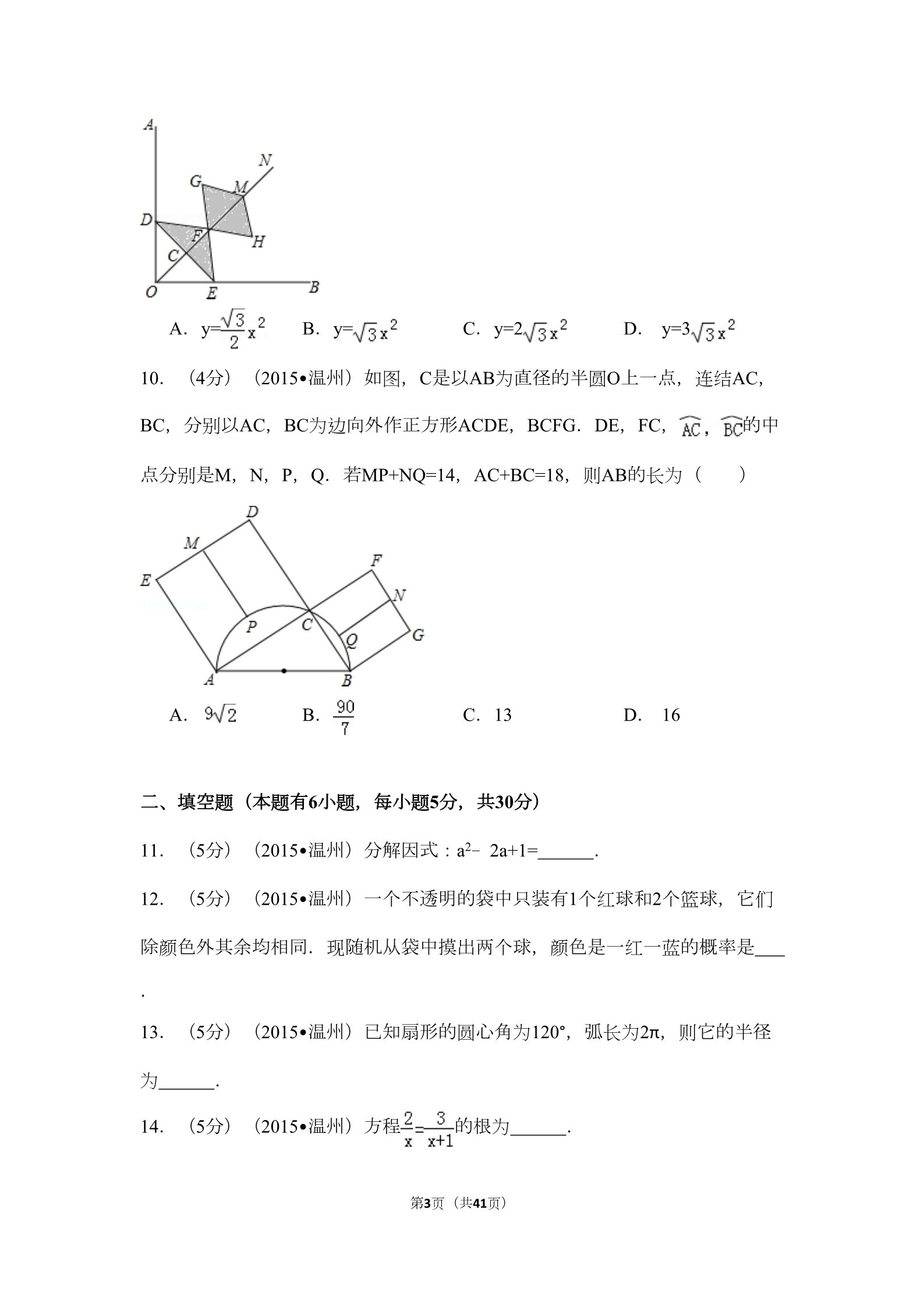
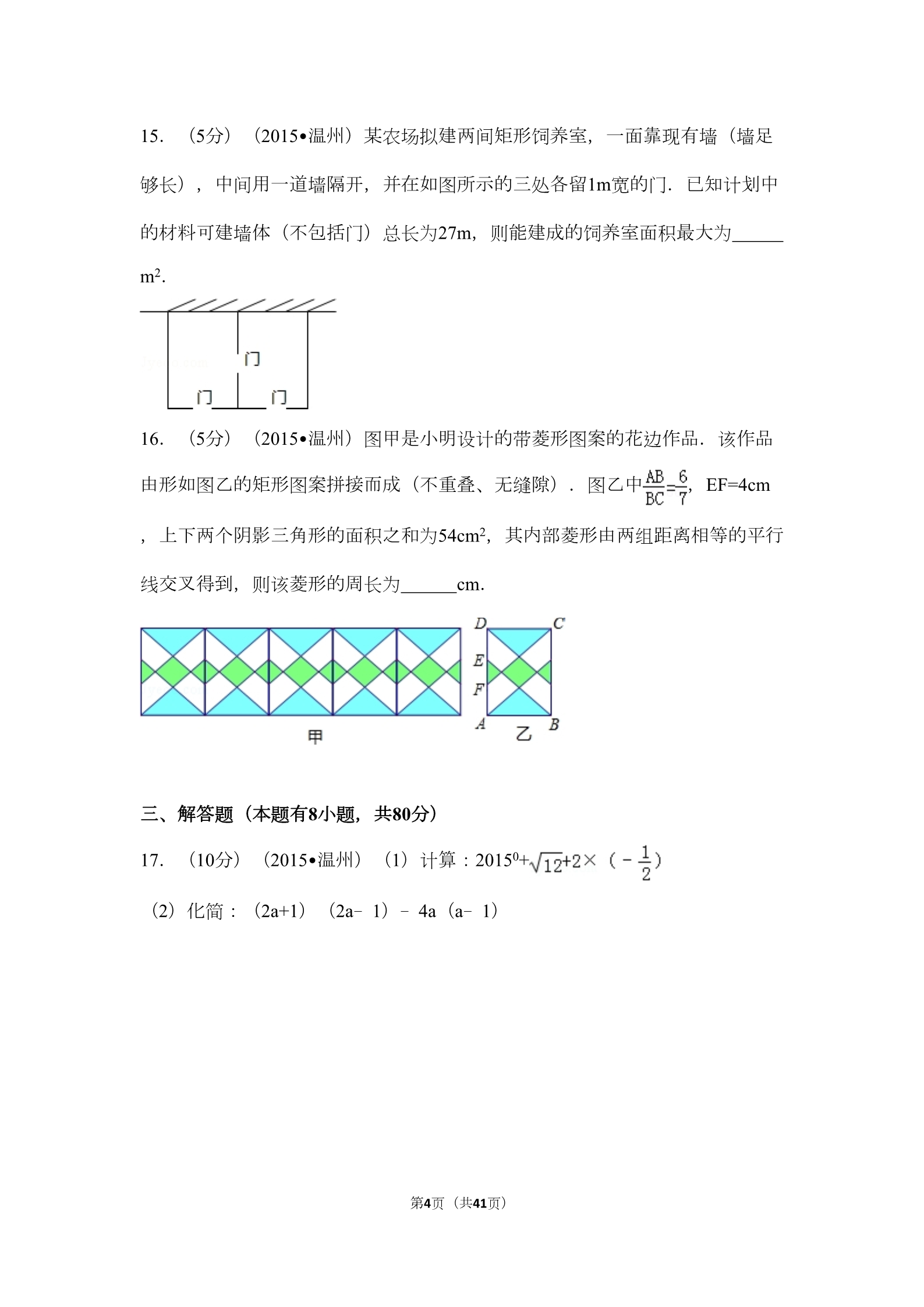
2015年浙江省温州市中考数学试卷（含解析版）

2015年浙江省温州市中考数学试卷一、选择题（本题有10小题，每小题4分，共40分） 1．（4分）（2015•温州）给出四个数0，，﹣1，其中最小的是（　　）　 A．0 B． C．1 D． ﹣1 2．（4分）（2015•温州）将一个长方体内部挖去一个圆柱（如图所示），它的主视图是（　　）　 A． B． C． D． 3．（4分）（2015•温州）某校学生参加体育兴趣小组情况的统计图如图所示，若参加人数最少的小组有25人，则参加人数最多的小组有（　　）　 A．25人 B．35人 C．40人 D． 100人 4．（4分）（2015•温州）下列选项中的图形，不属于中心对称图形的是（　　）　 A．等边三角形 B．正方形 C．正六边形 D．圆 5．（4分）（2015•温州）如图，在△ABC中，∠C=90°，AB=5，BC=3，则cosA 的值是（　　）第1页（共41页）　 A． B． C． D． 6．（4分）（2015•温州）若关于x的一元二次方程4×2﹣4x+c=0有两个相等实数根，则c的值是（　　）　 A．﹣1 B．1 C．﹣4 D． 4 7．（4分）（2015•温州）不等式组　 A．x＜1 B．x≥3 的解是（　　） C．1≤x＜3 D． 1＜x≤3 8．（4分）（2015•温州）如图，点A的坐标是（2，0），△ABO是等边三角形，点B在第一象限．若反比例函数y= 的图象经过点B，则k的值是（　　）　 A．1 B．2 C． D． 9．（4分）（2015•温州）如图，在Rt∠AOB的平分线ON上依次取点C，F，M ，过点C作DE⊥OC，分别交OA，OB于点D，E，以FM为对角线作菱形FGMH．已知∠DFE=∠GFH=120°，FG=FE，设OC=x，图中阴影部分面积为y，则y与x之间的函数关系式是（　　）第2页（共41页）　 A．y= 10．（4分）（2015•温州）如图，C是以AB为直径的半圆O上一点，连结AC， BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FC，的中点分别是M，N，P，Q．若MP+NQ=14，AC+BC=18，则AB的长为（　　） B．y= C．y=2 D． y=3 　 A． B． C．13 D． 16 二、填空题（本题有6小题，每小题5分，共30分） 11．（5分）（2015•温州）分解因式：a2﹣2a+1=　． 12．（5分）（2015•温州）一个不透明的袋中只装有1个红球和2个篮球，它们除颜色外其余均相同．现随机从袋中摸出两个球，颜色是一红一蓝的概率是　．13．（5分）（2015•温州）已知扇形的圆心角为120°，弧长为2π，则它的半径为　　． 14．（5分）（2015•温州）方程的根为　．第3页（共41页） 15．（5分）（2015•温州）某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为　m2． 16．（5分）（2015•温州）图甲是小明设计的带菱形图案的花边作品．该作品由形如图乙的矩形图案拼接而成（不重叠、无缝隙）．图乙中，EF=4cm ，上下两个阴影三角形的面积之和为54cm2，其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为　cm．　三、解答题（本题有8小题，共80分） 17．（10分）（2015•温州）（1）计算：20150+ （2）化简：（2a+1）（2a﹣1）﹣4a（a﹣1）　第4页（共41页） 18．（8分）（2015•温州）如图，点C，E，F，B在同一直线上，点A，D在BC 异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．　19．（8分）（2015•温州）某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：体能笔试面试甲乙丙83 85 80 79 80 90 90 75 73 （1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分．根据规定，请你说明谁将被录用．　第5页（共41页） 20．（8分）（2015•温州）各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形．如何计算它的面积？奥地利数学家皮克（G•Pick，1 859～1942年）证明了格点多边形的面积公式S=a+ b﹣1，其中a表示多边形内部的格点数，b表示多边形边界上的格点数，S表示多边形的面积．如图，a=4， b=6，S=4+ ×6﹣1=6 （1）请在图中画一个格点正方形，使它的内部只含有4个格点，并写出它的面积．（2）请在图乙中画一个格点三角形，使它的面积为，且每条边上除顶点外无其它格点．（注：图甲、图乙在答题纸上） 21．（10分）（2015•温州）如图，AB是半圆O的直径，CD⊥AB于点C，交半圆于点E，DF切半圆于点F．已知∠AEF=135°．（1）求证：DF∥AB；（2）若OC=CE，BF= ，求DE的长．第6页（共41页）　22．（10分）（2015•温州）某农业观光园计划将一块面积为900m2的圆圃分成 A，B，C三个区域，分别种植甲、乙、丙三种花卉，且每平方米栽种甲3株或乙 6株或丙12株．已知B区域面积是A区域面积的2倍．设A区域面积为x（m2）．（1）求该园圃栽种的花卉总株数y关于x的函数表达式．（2）若三种花卉共栽种6600株，则A，B，C三个区域的面积分别是多少？（3）若三种花卉的单价（都是整数）之和为45元，且差价均不超过10元，在（ 2）的前提下，全部栽种共需84000元．请写出甲、乙、丙三种花卉中，种植面积最大的花卉总价．　23．（12分）（2015•温州）如图，抛物线y=﹣x2+6x交x轴正半轴于点A，顶点为M，对称轴MB交x轴于点B．过点C（2，0）作射线CD交MB于点D（D在x轴上方），OE∥CD交MB于点E，EF∥x轴交CD于点F，作直线MF．（1）求点A，M的坐标．（2）当BD为何值时，点F恰好落在该抛物线上？第7页（共41页）（3）当BD=1时 ①求直线MF的解析式，并判断点A是否落在该直线上． ②延长OE交FM于点G，取CF中点P，连结PG，△FPG，四边形DEGP，四边形 OCDE的面积分别记为S1，S2，S3，则S1：S2：S3=　3：4：8　．　24．（14分）（2015•温州）如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O．点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交第8页（共41页） AB右侧的圆弧于点E．在射线CD上取点F，使DF= CD，以DE，DF为邻边作矩形DEGF．设AQ=3x．（1）用关于x的代数式表示BQ，DF．（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．（3）在点P的整个运动过程中， ①当AP为何值时，矩形DEGF是正方形？ ②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）．　第9页（共41页） 2015年浙江省温州市中考数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题4分，共40分） 1．（4分）（2015•温州）给出四个数0，，﹣1，其中最小的是（　　）　 A．0 B． C．1 D． ﹣1 【考点】实数大小比较．. 【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．【解答】解：根据实数比较大小的方法，可得 ﹣1＜0＜，∴四个数0，故选：D．，﹣1，其中最小的是﹣1．【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．　2．（4分）（2015•温州）将一个长方体内部挖去一个圆柱（如图所示），它的主视图是（　　）　 A． B． C． D．第10页（共41页）【考点】简单组合体的三视图．. 【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得主视图为长方形，中间有两条垂直地面的虚线．故选A．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．　3．（4分）（2015•温州）某校学生参加体育兴趣小组情况的统计图如图所示，若参加人数最少的小组有25人，则参加人数最多的小组有（　　）　 A．25人 B．35人 C．40人 D． 100人【考点】扇形统计图．. 【分析】根据参加足球的人数除以参加足球所长的百分比，可得参加兴趣小组的总人数，参加兴趣小组的总人数乘以参加乒乓球所占的百分比，可得答案．【解答】解：参加兴趣小组的总人数25÷25%=100（人），参加乒乓球小组的人数100×（1﹣25%﹣35%）=40（人），故选：C．【点评】本题考查了扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键，扇形统计图直接反映部分占总体的百分比大小．第11页（共41页）　4．（4分）（2015•温州）下列选项中的图形，不属于中心对称图形的是（　　）　 A．等边三角形 B．正方形 C．正六边形 D．圆【考点】中心对称图形．. 【分析】根据中心对称图形的概念求解．【解答】解：A、不是中心对称图形，故本选项正确； B、是中心对称图形，故本选项错误； C、是中心对称图形，故本选项错误； D、是中心对称图形，故本选项错误．故选A．【点评】本题考查了中心对称图形的概念：中心对称图形是要寻找对称中心，旋转180度后与原图重合．　5．（4分）（2015•温州）如图，在△ABC中，∠C=90°，AB=5，BC=3，则cosA 的值是（　　）　 A． B． C． D．【考点】锐角三角函数的定义．. 【分析】根据锐角的余弦等于邻边比斜边求解即可．第12页（共41页）【解答】解：∵AB=5，BC=3， ∴AC=4， ∴cosA= =．故选D．【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边　6．（4分）（2015•温州）若关于x的一元二次方程4×2﹣4x+c=0有两个相等实数根，则c的值是（　　）　 A．﹣1 B．1 C．﹣4 D． 4 【考点】根的判别式．. 【分析】根据判别式的意义得到△=42﹣4×4c=0，然后解一次方程即可．【解答】解：∵一元二次方程4×2﹣4x+c=0有两个相等实数根， ∴△=42﹣4×4c=0， ∴c=1，故选B．【点评】本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac ：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．　7．（4分）（2015•温州）不等式组　 A．x＜1 B．x≥3 的解是（　　） C．1≤x＜3 D． 1＜x≤3 第13页（共41页）【考点】解一元一次不等式组．. 【分析】先求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组的解集即可．【解答】解： ∵解不等式①得：x＞1，解不等式②得：x≤3， ∴不等式组的解集为1＜x≤3，故选D．【点评】本题考查了解一元一次不等式组的应用，解此题的关键是能根据不等式的解集求出不等式组的解集，难度适中．　8．（4分）（2015•温州）如图，点A的坐标是（2，0），△ABO是等边三角形，点B在第一象限．若反比例函数y= 的图象经过点B，则k的值是（　　）　 A．1 B．2 C． D．【考点】反比例函数图象上点的坐标特征；等边三角形的性质．. 【分析】首先过点A作BC⊥OA于点C，根据AO=2，△ABO是等边三角形，得出 B点坐标，进而求出反比例函数解析式．【解答】解：过点A作BC⊥OA于点C，第14页（共41页） ∵点A的坐标是（2，0）， ∴AO=2， ∵△ABO是等边三角形， ∴OC=1，BC= ，∴点B的坐标是（1，），把（1，）代入y= ，得k= ．故选C．【点评】此题主要考查了反比例函数的综合应用、等边三角形的性质以及图象上点的坐标特点等知识，根据已知表示出B点坐标是解题关键．　9．（4分）（2015•温州）如图，在Rt∠AOB的平分线ON上依次取点C，F，M ，过点C作DE⊥OC，分别交OA，OB于点D，E，以FM为对角线作菱形FGMH．已知∠DFE=∠GFH=120°，FG=FE，设OC=x，图中阴影部分面积为y，则y与x之间的函数关系式是（　　）　 A．y= B．y= C．y=2 D． y=3 【考点】菱形的性质；等边三角形的判定与性质；解直角三角形．. 第15页（共41页）【分析】由在Rt∠AOB的平分线ON上依次取点C，F，M，过点C作DE⊥OC，可得△OCD与△OCE是等腰直角三角形，即可得OC垂直平分DE，求得DE=2x，再由∠DFE=∠GFH=120°，可求得C与DF，EF的长，继而求得△DF的面积，再由菱形FGMH中，FG=FE，得到△FGM是等边三角形，即可求得其面积，继而求得答案．【解答】解：∵ON是Rt∠AOB的平分线， ∴∠DOC=∠EOC=45°， ∵DE⊥OC， ∴∠ODC=∠OEC=45°， ∴CD=CE=OC=x， ∴DF=EF，DE=CD+CE=2x， ∵∠DFE=∠GFH=120°， ∴∠CEF=30°， ∴CF=CE•tan30°= x， ∴EF=2CF= x， ∴S△DEF= DE•CF= x2， ∵四边形FGMH是菱形， ∴FG=MG=FE= x， ∵∠G=180°﹣∠GFH=60°， ∴△FMG是等边三角形， ∴S△FGH =x2， ∴S菱形FGMH =x2， ∴S阴影=S△DEF+S菱形FGMH 故选B． =x2．第16页（共41页）【点评】此题考查了菱形的性质、等腰直角三角形的性质、等边三角形的判定与性质以及三角函数等知识．注意证得△OCD与△OCE是等腰直角三角形，△FG M是等边三角形是关键．　10．（4分）（2015•温州）如图，C是以AB为直径的半圆O上一点，连结AC， BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FC，的中点分别是M，N，P，Q．若MP+NQ=14，AC+BC=18，则AB的长为（　　）　 A． B． C．13 D． 16 【考点】梯形中位线定理．. 【分析】连接OP，OQ，根据DE，FC，的中点分别是M，N，P，Q得到 OP⊥AC，OQ⊥BC，从而得到H、I是AC、BD的中点，利用中位线定理得到OH +OI= （AC+BC）=9和PH+QI，从而利用AB=OP+OQ=OH+OI+PH+QI求解．【解答】解：连接OP，OQ， ∵DE，FC，的中点分别是M，N，P，Q， ∴OP⊥AC，OQ⊥BC， ∴H、I是AC、BD的中点， ∴OH+OI= （AC+BC）=9， ∵MH+NI=AC+BC=18，MP+NQ=14，第17页（共41页） ∴PH+QI=18﹣14=4， ∴AB=OP+OQ=OH+OI+PH+QI=9+4=13，故选C．【点评】本题考查了中位线定理，解题的关键是正确的作出辅助线，题目中还考查了垂径定理的知识，难度不大．　二、填空题（本题有6小题，每小题5分，共30分） 11．（5分）（2015•温州）分解因式：a2﹣2a+1=　（a﹣1）2　．【考点】因式分解-运用公式法．. 专题：计算题．【分析】观察原式发现，此三项符合差的完全平方公式a2﹣2ab+b2=（a﹣b）2，即可把原式化为积的形式．【解答】解：a2﹣2a+1=a2﹣2×1×a+12=（a﹣1）2．故答案为：（a﹣1）2．【点评】本题考查了完全平方公式分解因式，熟练掌握完全平方公式的结构特点是解题的关键．　第18页（共41页） 12．（5分）（2015•温州）一个不透明的袋中只装有1个红球和2个篮球，它们除颜色外其余均相同．现随机从袋中摸出两个球，颜色是一红一蓝的概率是　　．【考点】列表法与树状图法．. 【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与随机从袋中摸出两个球，颜色是一红一蓝的情况，再利用概率公式即可求得答案．【解答】解：画树状图得： ∵共有6种等可能的结果，随机从袋中摸出两个球，颜色是一红一蓝的有4种情况，∴随机从袋中摸出两个球，颜色是一红一蓝的概率是： = ．故答案为：．【点评】此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．　13．（5分）（2015•温州）已知扇形的圆心角为120°，弧长为2π，则它的半径为　3　．【考点】弧长的计算．. 【分析】根据弧长公式代入求解即可．第19页（共41页）【解答】解：∵L= ∴R= =3．故答案为：3．，【点评】本题考查了弧长的计算，解答本题的关键是掌握弧长公式：L= ．　14．（5分）（2015•温州）方程的根为　x=2　．【考点】解分式方程．. 【分析】观察可得最简公分母是x（x+1），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．【解答】解：去分母得：2（x+1）=3x 即2x+2=3x 解得：x=2 经检验：x=2是原方程的解．故答案是：x=2 【点评】（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．　15．（5分）（2015•温州）某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为　75　 m2．第20页（共41页）【考点】二次函数的应用．. 【分析】设垂直于墙的材料长为x米，则平行于墙的材料长为27+3﹣3x=30﹣3x ，表示出总面积S=x（30﹣3x）=﹣3×2+30x=﹣3（x﹣5）2+75即可求得面积的最值．【解答】解：设垂直于墙的材料长为x米，则平行于墙的材料长为27+3﹣3x=30﹣3x，则总面积S=x（30﹣3x）=﹣3×2+30x=﹣3（x﹣5）2+75，故饲养室的最大面积为75平方米，故答案为：75．【点评】本题考查了二次函数的应用，解题的关键是从实际问题中抽象出函数模型，难度不大．　16．（5分）（2015•温州）图甲是小明设计的带菱形图案的花边作品．该作品由形如图乙的矩形图案拼接而成（不重叠、无缝隙）．图乙中，EF=4cm ，上下两个阴影三角形的面积之和为54cm2，其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为　cm．第21页（共41页）【考点】菱形的性质；矩形的性质．. 【分析】首先取CD的中点G，连接HG，设AB=6acm，则BC=7acm，中间菱形的对角线HI的长度为xcm；然后根据GH∥BC，可得x=3.5a﹣2；再根据上下两个阴影三角形的面积之和为54cm2，可得a（7a﹣x）=18，据此求出a、x的值各是多少；最后根据AM∥FC，求出HK的长度，再用HK的长度乘以4，求出该菱形的周长为多少即可．【解答】解：如图乙，取CD的中点G，连接HG，，设AB=6acm，则BC=7acm，中间菱形的对角线HI的长度为xcm， ∵BC=7acm，MN=EF=4cm， ∴CN= ，∵GH∥BC， ∴∴，，∴x=3.5a﹣2…（1）； ∵上下两个阴影三角形的面积之和为54cm2， ∴6a•（7a﹣x）÷2=54， ∴a（7a﹣x）=18…（2）；由（1）（2），可得 a=2，x=5，第22页（共41页） ∴CD=6×2=12（cm），CN= ，∴DN= =15（cm），又∵DH= ==7.5（cm）， ∴HN=15﹣7.5=7.5（cm）， ∵AM∥FC， ∴，∴HK= ，∴该菱形的周长为：（cm）．故答案为： =．【点评】（1）此题主要考查了菱形的性质和应用，要熟练掌握，解答此题的关键是要明确：①菱形具有平行四边形的一切性质；②菱形的四条边都相等； ③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．（2）此题还考查了矩形的性质和应用，要熟练掌握，解答此题的关键是要明确：①平行四边形的性质矩形都具有；②角：矩形的四个角都是直角；③边：邻边垂直； ④对角线：矩形的对角线相等；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．　三、解答题（本题有8小题，共80分）第23页（共41页） 17．（10分）（2015•温州）（1）计算：20150+ （2）化简：（2a+1）（2a﹣1）﹣4a（a﹣1）【考点】整式的混合运算；实数的运算．. 【分析】（1）先算乘方、化简二次根式与乘法，最后算加法；（2）利用平方差公式和整式的乘法计算，进一步合并得出答案即可．【解答】解：（1）原式=1+2 ﹣1 =2 ；（2）原式=4a2﹣1﹣4a2+4a =4a﹣1．【点评】此题考查整式的混合运算，掌握运算顺序与计算方法是解决问题的关键．　18．（8分）（2015•温州）如图，点C，E，F，B在同一直线上，点A，D在BC 异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．【考点】全等三角形的判定与性质．. 【分析】（1）易证得△ABE≌△CDF，即可得AB=CD；第24页（共41页）（2）易证得△ABE≌△CDF，即可得AB=CD，又由AB=CF，∠B=30°，即可证得 △ABE是等腰三角形，解答即可．【解答】证明：（1）∵AB∥CD， ∴∠B=∠C，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS）， ∴AB=CD；（2）∵△ABE≌△CDF， ∴AB=CD，BE=CF， ∵AB=CF，∠B=30°， ∴AB=BE， ∴△ABE是等腰三角形， ∴∠D= ．【点评】此题考查全等三角形问题，关键是根据AAS证明三角形全等，再利用全等三角形的性质解答．　19．（8分）（2015•温州）某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：体能笔试面试甲乙丙83 85 80 79 80 90 90 75 73 （1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．第25页（共41页）（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分．根据规定，请你说明谁将被录用．【考点】加权平均数．. 【分析】（1）代入求平均数公式即可求出三人的平均成绩，比较得出结果；（2）由于甲的面试成绩低于80分，根据公司规定甲被淘汰；再将乙与丙的总成绩按比例求出测试成绩，比较得出结果．【解答】解：（1）甲=（83+79+90）÷3=84，乙=（85+80+75）÷3=80，丙=（80+90+73）÷3=81．从高到低确定三名应聘者的排名顺序为：甲，丙，乙；（2）∵该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分， ∴甲淘汰；乙成绩=85×60%+80×30%+75×10%=82.5，丙成绩=80×60%+90×30%+73×10%=82.3，乙将被录取．【点评】本题考查了算术平均数和加权平均数的计算．平均数等于所有数据的和除以数据的个数．　20．（8分）（2015•温州）各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形．如何计算它的面积？奥地利数学家皮克（G•Pick，1 859～1942年）证明了格点多边形的面积公式S=a+ b﹣1，其中a表示多边形内第26页（共41页）部的格点数，b表示多边形边界上的格点数，S表示多边形的面积．如图，a=4， b=6，S=4+ ×6﹣1=6 （1）请在图中画一个格点正方形，使它的内部只含有4个格点，并写出它的面积．（2）请在图乙中画一个格点三角形，使它的面积为，且每条边上除顶点外无其它格点．（注：图甲、图乙在答题纸上）【考点】作图—应用与设计作图．. 【分析】（1）根据皮克公式画图计算即可；（2）根据题意可知a=3，b=3，画出满足题意的图形即可．【解答】解：（1）如图所示，a=4，b=4，S=4+ ×4﹣1=5；（2）因为S= ，b=3，所以a=3，如图所示，第27页（共41页）【点评】本题考查了应用与设计作图，关键是理解皮克公式，根据题意求出a、 b的值．　21．（10分）（2015•温州）如图，AB是半圆O的直径，CD⊥AB于点C，交半圆于点E，DF切半圆于点F．已知∠AEF=135°．（1）求证：DF∥AB；（2）若OC=CE，BF= ，求DE的长．【考点】切线的性质．. 【分析】（1）证明：连接OF，根据圆内接四边形的性质得到∠AEF+∠B=180° ，由于∠AEF=135°，得出∠B=45°，于是得到∠AOF=2∠B=90°，由DF切⊙O于F ，得到∠DFO=90°，由于DC⊥AB，得到∠DCO=90°，于是结论可得；（2）过E作EM⊥BF于M，由四边形DCOF是矩形，得到OF=DC=OA，由于OC= CE，推出AC=DE，设DE=x，则AC=x，在Rt△FOB中，∠FOB=90°，OF=OB，B F=2 ，由勾股定理得：OF=OB=2，则AB=4，BC=4﹣x，由于AC=DE，OCDF 第28页（共41页） =CE，由勾股定理得：AE=EF，通过Rt△ECA≌Rt△EMF，得出AC=MF=DE=x，在Rt△ECB和Rt△EMB中，由勾股定理得：BC=BM，问题可得．【解答】（1）证明：连接OF， ∵A、E、F、B四点共圆， ∴∠AEF+∠B=180°， ∵∠AEF=135°， ∴∠B=45°， ∴∠AOF=2∠B=90°， ∵DF切⊙O于F， ∴∠DFO=90°， ∵DC⊥AB， ∴∠DCO=90°，即∠DCO=∠FOC=∠DFO=90°， ∴四边形DCOF是矩形， ∴DF∥AB；（2）解：过E作EM⊥BF于M， ∵四边形DCOF是矩形， ∴OF=DC=OA， ∵OC=CE， ∴AC=DE，设DE=x，则AC=x， ∵在Rt△FOB中，∠FOB=90°，OF=OB，BF=2 ，由勾股定理得：OF=OB=2，则AB=4，BC=4﹣x， ∵AC=DE，OCDF=CE， ∴由勾股定理得：AE=EF，第29页（共41页） ∴∠ABE=∠FBE， ∵EC⊥AB，EM⊥BF ∴EC=EM，∠ECB=∠M=90°，在Rt△ECA和Rt△EMF中 ∴Rt△ECA≌Rt△EMF， ∴AC=MF=DE=x，在Rt△ECB和Rt△EMB中，由勾股定理得：BC=BM， ∴BF=BM﹣MF=BC﹣MF=4﹣x﹣x=2 ，解得：x=2﹣ 即DE=2﹣ ，．【点评】本题考查了圆周角性质，圆内接四边形的性质，全等三角形的性质和判定，角平分线性质，矩形的性质和判定的应用，正确的作出辅助线是解题的关键．　第30页（共41页） 22．（10分）（2015•温州）某农业观光园计划将一块面积为900m2的圆圃分成 A，B，C三个区域，分别种植甲、乙、丙三种花卉，且每平方米栽种甲3株或乙 6株或丙12株．已知B区域面积是A区域面积的2倍．设A区域面积为x（m2）．（1）求该园圃栽种的花卉总株数y关于x的函数表达式．（2）若三种花卉共栽种6600株，则A，B，C三个区域的面积分别是多少？（3）若三种花卉的单价（都是整数）之和为45元，且差价均不超过10元，在（ 2）的前提下，全部栽种共需84000元．请写出甲、乙、丙三种花卉中，种植面积最大的花卉总价．【考点】一次函数的应用．. 【分析】（1）设A区域面积为x，则B区域面积是2x，C区域面积是900﹣3x，根据每平方米栽种甲3株或乙6株或丙12株，即可解答；（2）当y=6600时，即﹣21x+10800=6600，解得：x=200，则2x=400，900﹣3x= 300，即可解答；（3）设三种花卉的单价分别为a元、b元、c，根据根据题意得：，整理得：3b+5c=95，根据三种花卉的单价（都是整数）之和为45元，且差价均不超过10元，所以b=15，c=10，a=20，即可解答．【解答】解：（1）y=3x+12x+12（900﹣3x）=﹣21x+10800．（2）当y=6600时，即﹣21x+10800=6600，解得：x=200， ∴2x=400，900﹣3x=300，答：A，B，C三个区域的面积分别是200m2，400m2，300m2．第31页（共41页）（3）设三种花卉的单价分别为a元、b元、c元，在（2）的前提下，分别种植甲、乙、丙三种花卉的株数为600株，2400株，3600株，根据题意得：，整理得：3b+5c=95， ∵三种花卉的单价（都是整数）之和为45元，且差价均不超过10元， ∴b=15，c=10， ∴a=20， ∴种植面积最大的花卉总价为：2400×15=36000（元），答：种植面积最大的花卉总价为36000元．【点评】本题考查了一次函数的应用，解决本题的关键是关键题意，列出函数关系式和方程组．　23．（12分）（2015•温州）如图，抛物线y=﹣x2+6x交x轴正半轴于点A，顶点为M，对称轴MB交x轴于点B．过点C（2，0）作射线CD交MB于点D（D在x轴上方），OE∥CD交MB于点E，EF∥x轴交CD于点F，作直线MF．（1）求点A，M的坐标．（2）当BD为何值时，点F恰好落在该抛物线上？（3）当BD=1时 ①求直线MF的解析式，并判断点A是否落在该直线上． ②延长OE交FM于点G，取CF中点P，连结PG，△FPG，四边形DEGP，四边形 OCDE的面积分别记为S1，S2，S3，则S1：S2：S3=　3：4：8　．第32页（共41页）【考点】二次函数综合题．. 【分析】（1）在抛物线解析式中令y=0，容易求得A点坐标，再根据顶点式，可求得M点坐标；（2）由条件可证明四边形OCFE为平行四边形，可求得EF的点，可求得F点坐标，可得出BE的长，再利用平行线的性质可求得BD的长；（3）①由条件可求得F点坐标，可求得直线MF的解析式，把A点坐标代入其解析式可判断出A点在直线MF上；②由点的坐标结合勾股定理求得OE、GE、CD 、DM、MF的长，再结合面积公式可分别表示出S1，S2，S3，可求得答案．【解答】解：（1）令y=0，则﹣x2+6x=0，解得x=0或x=6， ∴A点坐标为（6，0），又∵y=﹣x2+6x=﹣（x﹣3）2+9， ∴M点坐标为（3，9）；（2）∵OE∥CF，OC∥EF， ∴四边形OCFE为平行四边形，且C（2，0）， ∴EF=OC=2，又B（3，0），第33页（共41页） ∴OB=3，BC=1， ∴F点的横坐标为5， ∵点F落在抛物线y=﹣x2+6x上， ∴F点的坐标为（5，5）， ∴BE=5， ∵OE∥CF， ∴=，即 = ， ∴BD= ；（3）①当BD=1时，由（2）可知BE=3BD=3， ∴F（5，3），设直线MF解析式为y=kx+b，把M、F两点坐标代入可得 ∴直线MF解析式为y=﹣3x+18， ∵当x=6时，y=﹣3×6+18=0， ∴点A落在直线MF上； ②如图所示，，解得，∵E（3，3），第34页（共41页） ∴直线OE解析式为y=x，联立直线OE和直线MF解析式可得 ∴G（，），，解得，∴OG= =，OE=CF=3 ，∴EG=OG﹣OE= ﹣3 =，∵= ， ∴CD= OE= ，∵P为CF中点， ∴PF= CF= ，∴DP=CF﹣CD﹣PF=3 ∵OG∥CF， ﹣﹣=，∴可设OG和CF之间的距离为h， ∴S△FPG= PF•h= × h= h，四边形DEGP= （EG+DP）h= ×（四边形OCDE= （OE+CD）h= （3 S+）h= h， S+）h=2 h， ∴S1，S2，S3= h： h：2 h=3：4：8，故答案为：3：4：8．【点评】本题主要考查二次函数的综合应用，涉及二次函数的性质、一元二次方程、平行四边形的判定和性质、平行线分线段成比例、待定系数法、勾股定理等知识点．在（1）中注意抛物线顶点式的应用，在（2）中求得F点的坐标是解题的关键，在（3）①中，求得直线MF的解析式是解题的关键，在②中利用第35页（共41页）两平行线间的距离为定值表示出S1，S2，S3是解题的关键．本题考查知识点较多，综合性质较强，难度较大．　24．（14分）（2015•温州）如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O．点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交 AB右侧的圆弧于点E．在射线CD上取点F，使DF= CD，以DE，DF为邻边作矩形DEGF．设AQ=3x．（1）用关于x的代数式表示BQ，DF．（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．（3）在点P的整个运动过程中， ①当AP为何值时，矩形DEGF是正方形？ ②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）．【考点】圆的综合题．. 【分析】（1）由AQ：AB=3：4，AQ=3x，易得AB=4x，由勾股定理得BQ，再由中位线的性质得AH=BH= AB，求得CD，FD；第36页（共41页）（2）利用（1）的结论，易得CQ的长，作OM⊥AQ于点M（如图1），则OM∥A B，由垂径定理得QM=AM= x，由矩形性质得OD=MC，利用矩形面积，求得x ，得出结论；（3）①点P在A点的右侧时（如图1），利用（1）（2）的结论和正方形的性质得2x+4=3x，得AP；点P在A点的左侧时，当点C在Q右侧，0＜x＜时（如图2 ），4﹣7x=3x，解得x，易得AP；当时（如图3），7﹣4x=3x，得AP；当点C在Q的左侧时，即x≥ （如图4），同理得AP； ②连接NQ，由点O到BN的弦心距为l，得NQ=2，当点N在AB的左侧时（如图5 ），过点B作BM⊥EG于点M，GM=x，BM=x，易得∠GBM=45°，BM∥AQ，易得AI=AB，求得IQ，由NQ得AP；当点N在AB的右侧时（如图6），过点B作BJ ⊥GE于点J，由GJ=x，BJ=4x得tan∠GBJ= ，利用（1）（2）中结论得AI=16x， QI=19x，解得x，得AP．【解答】解：（1）在Rt△ABQ中， ∵AQ：AB=3：4，AQ=3x， ∴AB=4x， ∴BQ=5x， ∵OD⊥m，m⊥l， ∴OD∥l， ∵OB=OQ， ∴=2x， ∴CD=2x， ∴FD= =3x；（2）∵AP=AQ=3x，PC=4，第37页（共41页） ∴CQ=6x+4，作OM⊥AQ于点M（如图1）， ∴OM∥AB， ∵⊙O是△ABQ的外接圆，∠BAQ=90°， ∴点O是BQ的中点， ∴QM=AM= x ∴OD=MC= ∴OE= BQ= ∴ED=2x+4，，，S矩形DEGF=DF•DE=3x（2x+4）=90，解得：x1=﹣5（舍去），x2=3， ∴AP=3x=9；（3）①若矩形DEGF是正方形，则ED=DF， I．点P在A点的右侧时（如图1）， ∴2x+4=3x，解得：x=4， ∴AP=3x=12； II．点P在A点的左侧时，当点C在Q右侧， 0＜x＜时（如图2）， ∵ED=4﹣7x，DF=3x， ∴4﹣7x=3x，解得：x= ， ∴AP= ；当 ≤x＜时（如图3），第38页（共41页） ∵ED=7﹣4x，DF=3x， ∴7﹣4x=3x，解得：x=1（舍去），当点C在Q的左侧时，即x≥ （如图4）， DE=7x﹣4，DF=3x， ∴7x﹣4=3x，解得：x=1， ∴AP=3，综上所述：当AP为12或或3时，矩形DEGF是正方形； ②连接NQ，由点O到BN的弦心距为l，得NQ=2，当点N在AB的左侧时（如图5），过点B作BM⊥EG于点M， ∵GM=x，BM=x， ∴∠GBM=45°， ∴BM∥AQ， ∴AI=AB=4x， ∴IQ=x， ∴NQ= =2， ∴x=2 ，∴AP=6 ；当点N在AB的右侧时（如图6），过点B作BJ⊥GE于点J， ∵GJ=x，BJ=4x， ∴tan∠GBJ= ， ∴AI=16x，∴QI=19x， ∴NQ= =2，第39页（共41页） ∴x= ，∴AP= ，综上所述：AP的长为6 或．第40页（共41页）【点评】本题主要考查了勾股定理，垂径定理，正方形的性质，中位线的性质等，结合图形，分类讨论是解答此题的关键．　第41页（共41页）