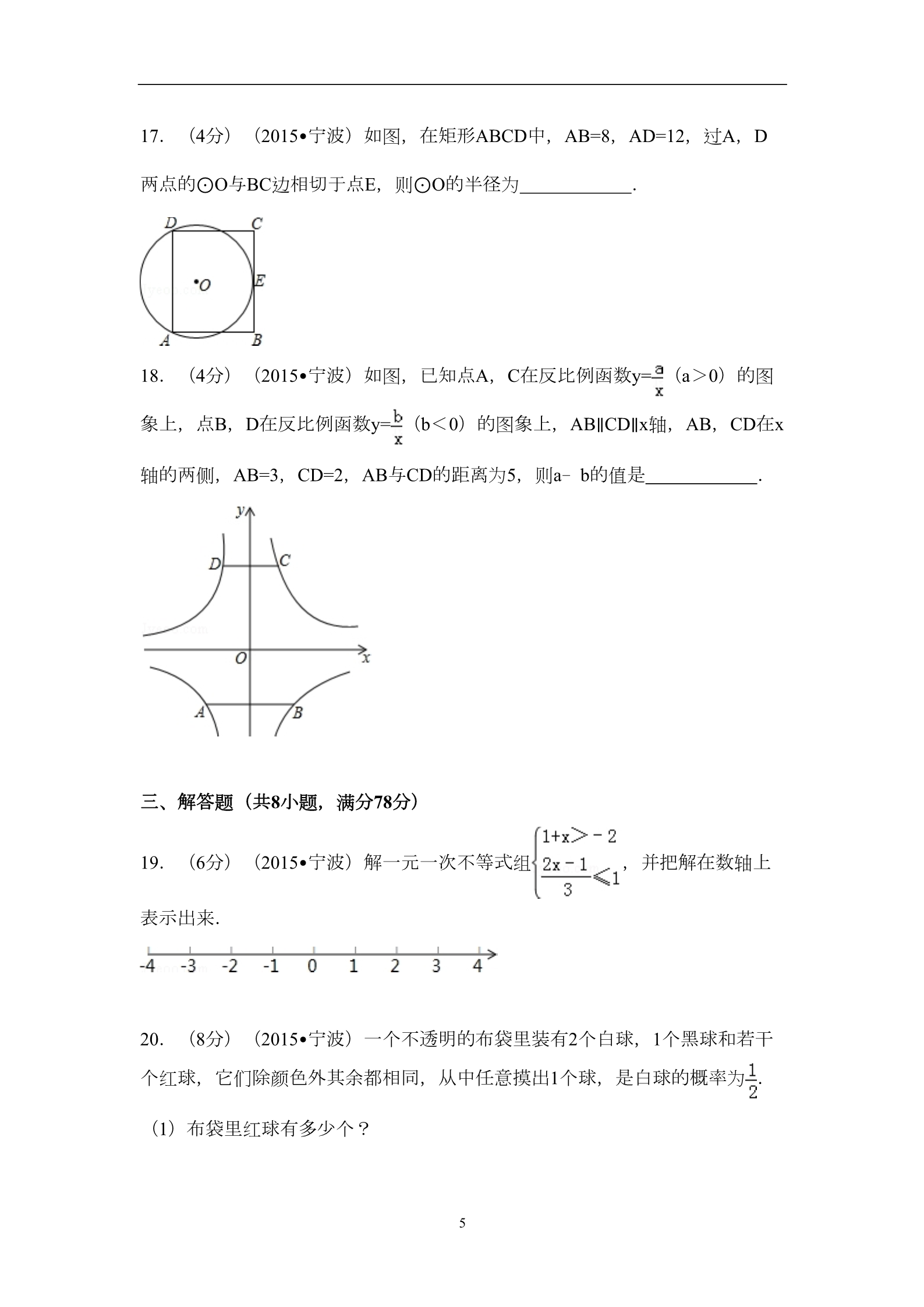
2015年浙江省宁波市中考数学试卷（含解析版）

2015年浙江省宁波市中考数学试卷 2bb  4ac 4a 参考公式：抛物线 y  ax2  bx  c 的顶点坐标为 ,.2a 一、选择题（共12小题，每小题4分，满分48分） 1．（4分）（2015•宁波）﹣ 的绝对值为（　　） ﹣3 　A B 3 CD﹣．．．．2．（4分）（2015•宁波）下列计算正确的是（　　） 2a﹣a=2 a•a3=a4 　A （a2）3=a5 BC （2a）2=4a D．．．．3．（4分）（2015•宁波）2015年中国高端装备制造业销售收入将超6万亿元，其中6万亿元用科学记数法可表示为（　　）　A 0.6×1013元 B 60×1011元 C 6×1012元 D 6×1013元．．．．4．（4分）（2015•宁波）在端午节到来之前，学校食堂推荐了A，B，C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购，下面的统计量中最值得关注的是（　　）　A 方差 B 平均数 C 中位数 D 众数．．．．5．（4分）（2015•宁波）如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（　　） 1　A BCD．．．．6．（4分）（2015•宁波）如图，直线a∥b，直线c分别与a，b相交，∠1=50°，则 ∠2的度数为（　　） 150° 130° 100° 50° 　A BCD．．．．7．（4分）（2015•宁波）如图，▱ABCD中，E，F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（　　） ∠1=∠2 　A BE=DF B BF=DE C AE=CF D．．．．8．（4分）（2015•宁波）如图，⊙O为△ABC的外接圆，∠A=72°，则∠BCO的度数为（　　） 15° 18° 20° 28° 　A BCD．．．．9．（4分）（2015•宁波）如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为（　　） 25πcm 　A 5cm B 10cm C 20cm D．．．．10．（4分）（2015•宁波）如图，将△ABC沿着过AB中点D的直线折叠，使点 A落在BC边上的A2处，称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去…，经过第 2015次操作后得到的折痕D2014 E2014到BC的距离记为h2015，到BC的距离记为h2015 ．若h1=1，则h2015的值为（　　）　A BC 1﹣ D 2﹣ ．．．．11．（4分）（2015•宁波）二次函数y=a（x﹣4）2﹣4（a≠0）的图象在2＜x＜3 这一段位于x轴的下方，在6＜x＜7这一段位于x轴的上方，则a的值为（　　） ﹣1 ﹣2 　A 1 BC 2 D．．．．312．（4分）（2015•宁波）如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（　　） ①② ②③ ①③ ①②③ 　A ．　BCD．．．二、填空题（共6小题，每小题4分，满分24分） 13．（4分）（2015•宁波）实数8的立方根是　　　　　　． 14．（4分）（2015•岳阳）分解因式：x2﹣9=　　　　　　． 15．（4分）（2015•宁波）命题“对角线相等的四边形是矩形”是　　　　　　命题（填“真”或“假”）． 16．（4分）（2015•宁波）如图，在数学活动课中，小敏为了测量校园内旗杆 AB的高度．站在教学楼的C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的俯角为30°．若旗杆与教学楼的距离为9m，则旗杆AB的高度是　　　　　　 m（结果保留根号） 417．（4分）（2015•宁波）如图，在矩形ABCD中，AB=8，AD=12，过A，D 两点的⊙O与BC边相切于点E，则⊙O的半径为　　　　　　． 18．（4分）（2015•宁波）如图，已知点A，C在反比例函数y= （a＞0）的图象上，点B，D在反比例函数y= （b＜0）的图象上，AB∥CD∥x轴，AB，CD在x 轴的两侧，AB=3，CD=2，AB与CD的距离为5，则a﹣b的值是　　　　　　．　三、解答题（共8小题，满分78分） 19．（6分）（2015•宁波）解一元一次不等式组，并把解在数轴上表示出来．　20．（8分）（2015•宁波）一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为．（1）布袋里红球有多少个？ 5（2）先从布袋中摸出1个球后不放回，再摸出1个球，请用列表法或画树状图等方法求出两次摸到的球都是白球的概率．　21．（8分）（2015•宁波）某校积极开展“阳光体育”活动，共开设了跳绳、足球、篮球、跑步四种运动项目，为了解学生最喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息未给出）．（1）求本次被调查的学生人数；（2）补全条形统计图；（3）该校共有1200名学生，请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少？　22．（10分）（2015•宁波）宁波火车站北广场将于2015年底投入使用，计划在广场内种植A，B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵 6（1）A，B两种花木的数量分别是多少棵？（2）如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或 B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？　23．（10分）（2015•宁波）已知抛物线y=（x﹣m）2﹣（x﹣m），其中m是常数．（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点；（2）若该抛物线的对称轴为直线x= ． ①求该抛物线的函数解析式； ②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点．　24．（10分）（2015•宁波）在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S=ma+nb﹣1，其中m，n为常数．（1）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；（2）利用（1）中的格点多边形确定m，n的值． 725．（12分）（2015•宁波）如图1，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，如果∠APB绕点P旋转时始终满足OA•OB=OP2，我们就把∠APB叫做∠MON的智慧角．（1）如图2，已知∠MON=90°，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，且∠APB=135°．求证：∠APB是∠M ON的智慧角．（2）如图1，已知∠MON=α（0°＜α＜90°），OP=2．若∠APB是∠MON的智慧角，连结AB，用含α的式子分别表示∠APB的度数和△AOB的面积．（3）如图3，C是函数y= （x＞0）图象上的一个动点，过C的直线CD分别交x 轴和y轴于A，B两点，且满足BC=2CA，请求出∠AOB的智慧角∠APB的顶点P的坐标． 8　26．（14分）（2015•宁波）如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以O M为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K．（1）若点M的坐标为（3，4）， ①求A，B两点的坐标； ②求ME的长．（2）若 =3，求∠OBA的度数．（3）设tan∠OBA=x（0＜x＜1）， =y，直接写出y关于x的函数解析式．　92015年浙江省宁波市中考数学试卷参考答案与试题解析　一、选择题（共12小题，每小题4分，满分48分） 1．（4分）（2015•宁波）﹣ 的绝对值为（　　） ﹣3 　A B 3 CD﹣．．．．考点：分析：解答：绝对值．菁优网版权所有根据当a是负有理数时，a的绝对值是它的相反数﹣a可得答．解：﹣ 的绝对值等于，故选：A．点评：此题主要考查了绝对值，关键是掌握①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数﹣a；③当a 是零时，a的绝对值是零．　2．（4分）（2015•宁波）下列计算正确的是（　　） 2a﹣a=2 a•a3=a4 　A （a2）3=a5 BC （2a）2=4a D．．．．考点：幂的乘方与积的乘方；合并同类项；同底数幂的乘法．菁优网版权所有根据同底数幂的乘法的性质，幂的乘方的性质，积的乘方的性质，合并同类项的法则，对各选项分析判断后利用排除法求解．分析： 236解答：解：A、（a ） =a ，故错误； 10 B、2a﹣a=a，故错误； C、（2a）2=4a2，故错误； D、正确；故选：D．点评：本题考查了合并同类项，同底数幂的乘法，幂的乘方，积的乘方，理清指数的变化是解题的关键．　3．（4分）（2015•宁波）2015年中国高端装备制造业销售收入将超6万亿元，其中6万亿元用科学记数法可表示为（　　）　A 0.6×1013元 B 60×1011元 C 6×1012元 D 6×1013元．．．．考点：科学记数法—表示较大的数．菁优网版权所有 n分析：科学记数法的表示形式为a×10 的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜ 1时，n是负数． 12 解答：解：将6万亿用科学记数法表示为：6×10 ．故选：C．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　11 4．（4分）（2015•宁波）在端午节到来之前，学校食堂推荐了A，B，C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购，下面的统计量中最值得关注的是（　　）　A 方差 B 平均数 C 中位数 D 众数．．．．考点：统计量的选择．菁优网版权所有分析：解答：学校食堂最值得关注的应该是哪种粽子爱吃的人数最多，即众数．解：由于众数是数据中出现次数最多的数，故学校食堂最值得关注的应该是统计调查数据的众数．故选D．点评：此题主要考查统计的有关知识，主要包括平均数、中位数、众数的意义．反映数据集中程度的统计量有平均数、中位数、众数等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．　5．（4分）（2015•宁波）如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（　　）　A BCD．．．．考点：简单组合体的三视图．菁优网版权所有 12 分析：解答：找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．解：从上面看易得上面一层有3个正方形，下面中间有一个正方形．故选A．点评：本题考查了三视图的知识，俯视图是从物体的上面看得到的视图．　6．（4分）（2015•宁波）如图，直线a∥b，直线c分别与a，b相交，∠1=50°，则 ∠2的度数为（　　） 150° 130° 100° 50° 　A BCD．．．．考点：分析：平行线的性质．菁优网版权所有先根据两直线平行同位角相等，求出∠3的度数，然后根据邻补角的定义即可求出∠2的度数．解：如图所示，解答： ∵a∥b，∠1=50°， ∴∠3=∠1=50°， ∵∠2+∠3=180°， ∴∠2=130°． 13 故选B．点评：此题考查了平行线的性质，解题的关键是：熟记两直线平行同位角相等，两直线平行内错角相等，两直线平行同旁内角互补．　7．（4分）（2015•宁波）如图，▱ABCD中，E，F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（　　） ∠1=∠2 　A BE=DF B BF=DE C AE=CF D．．．．考点：全等三角形的判定；平行四边形的性质．菁优网版权所有利用平行四边形的性质以及全等三角形的判定分别得出三角形全等，再进行选择即可．分析：解答：解：A、当BE=FD， ∵平行四边形ABCD中， ∴AB=CD，∠ABE=∠CDF，在△ABE和△CDF中，∴△ABE≌△CDF（SAS），故此选项错误； C、当AE=CF无法得出△ABE≌△CDF，故此选项符合题意； B、当BF=ED， ∴BE=DF， 14 ∵平行四边形ABCD中， ∴AB=CD，∠ABE=∠CDF，在△ABE和△CDF中，∴△ABE≌△CDF（SAS），故此选项错误； D、当∠1=∠2， ∵平行四边形ABCD中， ∴AB=CD，∠ABE=∠CDF，在△ABE和△CDF中，∴△ABE≌△CDF（ASA），故此选项错误；故选C．点评：本题考查了平行四边形的性质以及全等三角形的判定等知识，熟练掌握全等三角形的判定方法是解题关键．　8．（4分）（2015•宁波）如图，⊙O为△ABC的外接圆，∠A=72°，则∠BCO的度数为（　　） 15° 18° 20° 28° 　A BCD．．．．15 考点：圆周角定理．菁优网版权所有计算题．专题：分析：连结OB，如图，先根据圆周角定理得到∠BOC=2∠A=144°，然后根据等腰三角形的性质和三角形内角和定理计算∠BCO的度数．解：连结OB，如图，∠BOC=2∠A=2×72°=144°，解答：∵OB=OC， ∴∠CBO=∠BCO， ∴∠BCO= （180°﹣∠BOC）= ×（180°﹣144°）=18°．故选B．点评本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相：等，都等于这条弧所对的圆心角的一半．也考查了等腰三角形的性质．　9．（4分）（2015•宁波）如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为（　　） 5πcm D　A 5cm B 10cm C 20cm 16 ．．．．考点：圆锥的计算．菁优网版权所有由圆锥的几何特征，我们可得用半径为30cm，面积为300πcm2的扇形铁皮制作一个无盖的圆锥形容器，则圆锥的底面周长等于扇形的弧长，据此求得圆锥的底面圆的半径．分析：解答：解：设铁皮扇形的半径和弧长分别为R、l，圆锥形容器底面半径为r，则由题意得R=30，由 Rl=300π得l=20π；　由2πr=l得r=10cm；故选B．点评本题考查的知识点是圆锥的体积，其中根据已知制作一个无盖的圆锥形：容器的扇形铁皮的相关几何量，计算出圆锥的底面半径和高，是解答本题的关键．　10．（4分）（2015•宁波）如图，将△ABC沿着过AB中点D的直线折叠，使点 A落在BC边上的A2处，称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去…，经过第 2015次操作后得到的折痕D2014 E2014到BC的距离记为h2015，到BC的距离记为h2015 ．若h1=1，则h2015的值为（　　） 17 　A BC 1﹣ D 2﹣ ．．．．考点：相似三角形的判定与性质；三角形中位线定理；翻折变换（折叠问题）．菁优网版权所有专题：规律型．分析：根据中点的性质及折叠的性质可得DA=DA’=DB，从而可得∠ADA’=2∠B ，结合折叠的性质，∠ADA’=2∠ADE，可得∠ADE=∠B，继而判断DE∥BC ，得出DE是△ABC的中位线，证得AA1⊥BC，得到AA1=2，求出h1=2﹣1 =1，同理h2=2﹣ ，h3=2﹣ 折痕Dn﹣1 n﹣1到BC的距离hn=2﹣ 解：连接AA1， =2﹣ ，于是经过第n次操作后得到的 E，求得结果h2015=2﹣ ．解答：由折叠的性质可得：AA1⊥DE，DA=DA1，又∵D是AB中点， ∴DA=DB， ∴DB=DA1， ∴∠BA1D=∠B， ∴∠ADA1=2∠B，又∵∠ADA1=2∠ADE， ∴∠ADE=∠B， ∴DE∥BC， 18 ∴AA1⊥BC， ∴AA1=2， ∴h1=2﹣1=1，同理，h2=2﹣ ，h3=2﹣ =2﹣ ，…∴经过第n次操作后得到的折痕Dn﹣1 En﹣1到BC的距离hn=2﹣ ，∴h2015=2﹣ 故选D．，点评：本题考查了相似三角形的判定和性质，三角形中位线的性质，平行线等分线段定理，找出规律是解题的关键．　11．（4分）（2015•宁波）二次函数y=a（x﹣4）2﹣4（a≠0）的图象在2＜x＜3 这一段位于x轴的下方，在6＜x＜7这一段位于x轴的上方，则a的值为（　　） ﹣1 ﹣2 　A 1 BC 2 D．．．．考点：分析：抛物线与x轴的交点．菁优网版权所有根据抛物线顶点式得到对称轴为直线x=4，利用抛物线对称性得到抛物线在1＜x＜2这一段位于x轴的上方，而抛物线在2＜x＜3这一段位于x轴的下方，于是可得抛物线过点（2，0），然后把（2，0）代入y=a（x﹣ 19 4）2﹣4（a≠0）可求出a的值． 2解答：解：∵抛物线y=a（x﹣4） ﹣4（a≠0）的对称轴为直线x=4，而抛物线在6＜x＜7这一段位于x轴的上方， ∴抛物线在1＜x＜2这一段位于x轴的上方， ∵抛物线在2＜x＜3这一段位于x轴的下方， ∴抛物线过点（2，0），把（2，0）代入y=a（x﹣4）2﹣4（a≠0）得4a﹣4=0，解得a=1．故选A．点评：本题考查了抛物线与x轴的交点：求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．△=b2﹣4ac决定抛物线与x轴的交点个数： △=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x 轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．　12．（4分）（2015•宁波）如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（　　） ①② ②③ ①③ ①②③ 　A BCD．．．．考点：中心对称．菁优网版权所有 20 专题：应用题．分析：首先根据长方形被分割成3个正方形和2个长方形后仍是中心对称图形，可得A的对应点是A′，B的对应点是B′，判断出AB=A′B′；然后根据① 的长和②的边长的和等于原长方形的长，①的宽和②的边长的和等于原长方形的宽，可得①②的周长和等于原长方形的周长，据此判断即可．解答：解：如图，，∵长方形被分割成3个正方形和2个长方形后仍是中心对称图形， ∴A的对应点是A′，B的对应点是B′， ∴AB=A′B′， ∵①的长和②的边长的和等于原长方形的长，①的宽和②的边长的和等于原长方形的宽， ∴①②的周长和等于原长方形的周长， ∴分割后不用测量就能知道周长的图形的标号为①②，其余的图形的周长不用测量无法判断．故选：A．点评：此题主要考查了中心对称的性质和应用，要熟练掌握，解答此题的关键是要明确中心对称的性质：①关于中心对称的两个图形能够完全重合；②关于中心对称的两个图形，对应点的连线都经过对称中心，并且 21 被对称中心平分．　二、填空题（共6小题，每小题4分，满分24分） 13．（4分）（2015•宁波）实数8的立方根是　2　．考点：立方根．菁优网版权所有专题：常规题型．分析：根据立方根的定义解答．解答：解：∵23=8， ∴8的立方根是2．故答案为：2．点评：本题考查了立方根的定义，找出2的立方是8是解题的关键．　14．（4分）（2015•岳阳）分解因式：x2﹣9=　（x+3）（x﹣3）　．考点因式分解-运用公式法．菁优网版权所有：分析本题中两个平方项的符号相反，直接运用平方差公式分解因式．：解：x2﹣9=（x+3）（x﹣3）．解答：故答案为：（x+3）（x﹣3）．点评主要考查平方差公式分解因式，熟记能用平方差公式分解因式的多项式的：特征，即“两项、异号、平方形式”是避免错用平方差公式的有效方法．　22 15．（4分）（2015•宁波）命题“对角线相等的四边形是矩形”是　假　命题（填“真”或“假”）．考点：命题与定理．菁优网版权所有分析：举出反例即可得到该命题是假命题．解答：解：∵等腰梯形的对角线也相等， ∴“对角线相等的四边形是矩形”是假命题，故答案为：假；点评：本题考查了命题与定理的知识，解题的关键是知道如何判断一个命题的真假，是假命题时找到反例即可．　16．（4分）（2015•宁波）如图，在数学活动课中，小敏为了测量校园内旗杆 AB的高度．站在教学楼的C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的俯角为30°．若旗杆与教学楼的距离为9m，则旗杆AB的高度是　3 +9　 m（结果保留根号）考点：解直角三角形的应用-仰角俯角问题．菁优网版权所有分析：根据在Rt△ACD中，tan∠ACD= ，求出AD的值，再根据在Rt△BCD中 23 ，tan∠BCD= ，求出BD的值，最后根据AB=AD+BD，即可求出答案．解答：解：在Rt△ACD中， ∵tan∠ACD= ，∴tan30°= ，∴=，∴AD=3 m，在Rt△BCD中， ∵∠BCD=45°， ∴BD=CD=9m， ∴AB=AD+BD=3 +9（m）．故答案为：3 +9．点评：此题考查了解直角三角形的应用﹣仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．　17．（4分）（2015•宁波）如图，在矩形ABCD中，AB=8，AD=12，过A，D 两点的⊙O与BC边相切于点E，则⊙O的半径为　6.25　．考点：切线的性质；勾股定理；矩形的性质；垂径定理．菁优网版权所有分析：首先连接OE，并反向延长交AD于点F，连接OA，由在矩形ABCD中，过A，D两点的⊙O与BC边相切于点E，易得四边形CDFE是矩形，由垂径定理可求得AF的长，然后设⊙O的半径为x，则OE=EF﹣OE=8﹣x， 24 利用勾股定理即可得：（8﹣x）2+36=x2，继而求得答案．解：连接OE，并反向延长交AD于点F，连接OA， ∵BC是切线，解答： ∴OE⊥BC， ∴∠OEC=90°， ∵四边形ABCD是矩形， ∴∠C=∠D=90°， ∴四边形CDFE是矩形， ∴EF=CD=AB=8，OF⊥AD， ∴AF= AD= ×12=6，设⊙O的半径为x，则OE=EF﹣OE=8﹣x，在Rt△OAF中，OF2+AF2=OA2，则（8﹣x）2+36=x2，解得：x=6.25， ∴⊙O的半径为：6.25．故答案为：6.25．点评：此题考查了切线的性质、垂径定理、矩形的性质以及勾股定理．注意准确作出辅助线是解此题的关键．　25 18．（4分）（2015•宁波）如图，已知点A，C在反比例函数y= （a＞0）的图象上，点B，D在反比例函数y= （b＜0）的图象上，AB∥CD∥x轴，AB，CD在x 轴的两侧，AB=3，CD=2，AB与CD的距离为5，则a﹣b的值是　．考点：反比例函数图象上点的坐标特征．菁优网版权所有分析：设A（t，），则C（﹣t，﹣ ），B（，），D（﹣ ，﹣ ），结合相关线段的长度来求a﹣b的值．解答：解：设A（t，），则C（﹣t，﹣ ），B（，），D（﹣ ，﹣ ），依题意得，解得，所以a﹣b= ﹣（﹣ ）= 故答案是：．．26 点评：本题考查了反比例函数图象上点的坐标特征．此题借助于方程组来求得相关系数的．　三、解答题（共8小题，满分78分） 19．（6分）（2015•宁波）解一元一次不等式组，并把解在数轴上表示出来．考点解一元一次不等式组；在数轴上表示不等式的解集．菁优网版权所有：分析：别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．解答：解：由①得，x＞﹣3，由②得，x≤2，故此不等式组的解集为：﹣3＜x≤2．在数轴上表示为：点评本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小：大中间找；大大小小找不到”的原则是解答此题的关键．　20．（8分）（2015•宁波）一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为． 27 （1）布袋里红球有多少个？（2）先从布袋中摸出1个球后不放回，再摸出1个球，请用列表法或画树状图等方法求出两次摸到的球都是白球的概率．考点列表法与树状图法；概率公式．菁优网版权所有：分析（1）设红球的个数为x，根据白球的概率可得关于x的方程，解方程即可：；（2）画出树形图，即可求出两次摸到的球都是白球的概率．解答解：（1）设红球的个数为x，由题意可得：：，解得：x=1，即红球的个数为1个；（2）画树状图如下： ∴P（摸得两白）= =．点评此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的：列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比． 28 　21．（8分）（2015•宁波）某校积极开展“阳光体育”活动，共开设了跳绳、足球、篮球、跑步四种运动项目，为了解学生最喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息未给出）．（1）求本次被调查的学生人数；（2）补全条形统计图；（3）该校共有1200名学生，请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少？考点：条形统计图；用样本估计总体；扇形统计图．菁优网版权所有分析：（1）用喜欢跳绳的人数除以其所占的百分比即可求得被调查的总人数；（2）用总人数乘以足球所占的百分比即可求得喜欢足球的人数，用总数减去其他各小组的人数即可求得喜欢跑步的人数，从而补全条形统计图；（3）用样本估计总体即可确定最喜爱篮球的人数比最喜爱足球的人数多多少．解答：解：（1）观察条形统计图与扇形统计图知：喜欢跳绳的有10人，占25% 29 ，故总人数有10÷25%=40人；（2）喜欢足球的有40×30%=12人，喜欢跑步的有40﹣10﹣15﹣12=3人，故条形统计图补充为：（3）全校最喜爱篮球的人数比最喜爱足球的人数多1200× =90人．点评：本题考查了扇形统计图、条形统计图及用样本估计总体的知识，解题的关键是能够读懂两种统计图并从中整理出进一步解题的有关信息，难度不大．　22．（10分）（2015•宁波）宁波火车站北广场将于2015年底投入使用，计划在广场内种植A，B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵（1）A，B两种花木的数量分别是多少棵？（2）如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或 B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？ 30 考点：分析：分式方程的应用；二元一次方程组的应用．菁优网版权所有（1）首先设B花木数量为x棵，则A花木数量是（2x﹣600）棵，由题意得等量关系：种植A，B两种花木共6600棵，根据等量关系列出方程，再解即可；（2）首先设安排a人种植A花木，由题意得等量关系：a人种植A花木所用时间=（26﹣a）人种植B花木所用时间，根据等量关系列出方程，再解即可．解答：解：（1）设B花木数量为x棵，则A花木数量是（2x﹣600）棵，由题意得： x+2x﹣600=6600，解得：x=2400， 2x﹣600=4200，答：B花木数量为2400棵，则A花木数量是4200棵；（2）设安排a人种植A花木，由题意得： =，解得：a=14，经检验：a=14是原分式方程的解， 26﹣a=26﹣14=12，答：安排14人种植A花木，12人种植B花木．点评：此题主要考查了分式方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．注意不要忘记检验．　31 23．（10分）（2015•宁波）已知抛物线y=（x﹣m）2﹣（x﹣m），其中m是常数．（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点；（2）若该抛物线的对称轴为直线x= ． ①求该抛物线的函数解析式； ②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点．考点：抛物线与x轴的交点；二次函数图象与几何变换；待定系数法求二次函数解析式．菁优网版权所有专题：计算题．分析：（1）先把抛物线解析式化为一般式，再计算△的值，得到△=1＞0，于是根据△=b2﹣4ac决定抛物线与x轴的交点个数即可判断不论m为何值，该抛物线与x轴一定有两个公共点；（2）①根据对称轴方程得到=﹣ 到抛物线解析式； = ，然后解出m的值即可得 ②根据抛物线的平移规律，设抛物线沿y轴向上平移k个单位长度后，得到的抛物线与x轴只有一个公共点，则平移后抛物线解析式为y=x2﹣5x+6 +k，再利用抛物线与x轴的交点问题得到△=52﹣4（6+k）=0，然后解关于k的方程即可． 222解答：（1）证明：y=（x﹣m） ﹣（x﹣m）=x ﹣（2m+1）x+m +m， ∵△=（2m+1）2﹣4（m2+m）=1＞0， ∴不论m为何值，该抛物线与x轴一定有两个公共点； 32 （2）解：①∵x=﹣ = ， ∴m=2， ∴抛物线解析式为y=x2﹣5x+6； ②设抛物线沿y轴向上平移k个单位长度后，得到的抛物线与x轴只有一个公共点，则平移后抛物线解析式为y=x2﹣5x+6+k， ∵抛物线y=x2﹣5x+6+k与x轴只有一个公共点， ∴△=52﹣4（6+k）=0， ∴k= ，即把该抛物线沿y轴向上平移个单位长度后，得到的抛物线与x轴只有一个公共点．点评：本题考查了抛物线与x轴的交点：求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．△=b2﹣4ac决定抛物线与x轴的交点个数： △=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x 轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．　24．（10分）（2015•宁波）在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S=ma+nb﹣1，其中m，n为常数．（1）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；（2）利用（1）中的格点多边形确定m，n的值． 33 考点：分析：作图—应用与设计作图．菁优网版权所有（1）利用格点图形的定义结合三角形以及平行四边形面积求法得出即可；（2）利用已知图形，结合S=ma+nb﹣1得出关于m，n的关系式，进而求出即可．解答：解：（1）如图所示：；（2）∵格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S=ma+nb﹣1，其中m，n为常数， ∴三角形：S=3m+8n﹣1=6，平行四边形：S=3m+8n﹣1=6，菱形：S=5m +4n﹣1=6，则，解得：．点评：此题主要考查了应用设计与作图以及三角形、平行四边形面积求法和二元一次方程组的解法，正确得出关于m，n的方程组是解题关键． 34 　25．（12分）（2015•宁波）如图1，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，如果∠APB绕点P旋转时始终满足OA•OB=OP2，我们就把∠APB叫做∠MON的智慧角．（1）如图2，已知∠MON=90°，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，且∠APB=135°．求证：∠APB是∠M ON的智慧角．（2）如图1，已知∠MON=α（0°＜α＜90°），OP=2．若∠APB是∠MON的智慧角，连结AB，用含α的式子分别表示∠APB的度数和△AOB的面积．（3）如图3，C是函数y= （x＞0）图象上的一个动点，过C的直线CD分别交x 轴和y轴于A，B两点，且满足BC=2CA，请求出∠AOB的智慧角∠APB的顶点P的坐标．考点：反比例函数综合题．菁优网版权所有分析：（1）由角平分线求出∠AOP=∠BOP= ∠MON=45°，再证出∠OAP=∠OPB ，证明△AOP∽△POB，得出对应边成比例，得出OP2=OA•OB，即可得出结论；（2）由∠APB是∠MON的智慧角，得出，证出△AOP∽△POB，得出对应角相等∠OAP=∠OPB，即可得出∠APB=180°﹣ α；过点A作AH⊥ 35 OB于H，由三角形的面积公式得出：S△AOB= OB•AH，即可得出S△AOB =2sinα；（3）设点C（a，b），则ab=3，过点C作CH⊥OA于H；分两种情况： ①当点B在y轴正半轴上时；当点A在x轴的负半轴上时，BC=2CA不可能；当得A在x轴的正半轴上时；先求出，由平行线得出△ACH∽△ ABO，得出比例式： = ，得出OB=3b，OA= ，求出OA•O B= ，根据∠APB是∠AOB的智慧角，得出OP，即可得出点P的坐标； ②当点B在y轴的负半轴上时；由题意得出：AB=CA，由AAS证明△AC H≌△ABO，得出OB=CH=b，OA=AH= a，得出OA•OB= ，求出OP，即可得出点P的坐标．解答：（1）证明：∵∠MON=90°，P为∠MON的平分线上一点， ∴∠AOP=∠BOP= ∠MON=45°， ∵∠AOP+∠OAP+∠APO=180°， ∴∠OAP+∠APO=135°， ∵∠APB=135°， ∴∠APO+∠OPB=135°， ∴∠OAP=∠OPB， ∴△AOP∽△POB， ∴，∴OP2=OA•OB， ∴∠APB是∠MON的智慧角；（2）解：∵∠APB是∠MON的智慧角， ∴OA•OB=OP2， ∴，∵P为∠MON的平分线上一点， 36 ∴∠AOP=∠BOP= α， ∴△AOP∽△POB， ∴∠OAP=∠OPB， ∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°﹣ α，即∠APB=180°﹣ α；过点A作AH⊥OB于H，连接AB；如图1所示：则S△AOB= OB•AH= OB•OAsinα= OP2•sinα， ∵OP=2， ∴S△AOB=2sinα；（3）设点C（a，b），则ab=3，过点C作CH⊥OA于H；分两种情况： ①当点B在y轴正半轴上时；当点A在x轴的负半轴上时，如图2所示： BC=2CA不可能；当得A在x轴的正半轴上时，如图3所示： ∵BC=2CA， ∴，∵CH∥OB， ∴△ACH∽△ABO， ∴= ， ∴OB=3b，OA= ，∴OA•OB= •3b= =，∵∠APB是∠AOB的智慧角， ∴OP= ==，∵∠AOB=90°，OP平分∠AOB， ∴点P的坐标为：（，）； 37 ②当点B在y轴的负半轴上时，如图4所示： ∵BC=2CA， ∴AB=CA，在△ACH和△ABO中，，∴△ACH≌△ABO（AAS）， ∴OB=CH=b，OA=AH= a， ∴OA•OB= a•b= ， ∵∠APB是∠AOB的智慧角， ∴OP= ==，∵∠AOB=90°，OP平分∠AOB， ∴点P的坐标为：（，﹣ ）；综上所述：点P的坐标为：（，），或（，﹣ ）． 38 点评：本题是反比例函数综合题目，考查了角平分线的性质、相似三角形的判定与性质、新定义以及运用、三角形面积的计算、全等三角形的判定与性质等知识；本题难度较大，综合性强，特别是（3）中，需要通过作辅助线进行分类讨论，证明三角形相似和三角形全等才能得出结果．　26．（14分）（2015•宁波）如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以O M为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K．（1）若点M的坐标为（3，4）， ①求A，B两点的坐标； ②求ME的长．（2）若 =3，求∠OBA的度数．（3）设tan∠OBA=x（0＜x＜1）， =y，直接写出y关于x的函数解析式． 39 考点：圆的综合题；全等三角形的判定与性质；直角三角形斜边上的中线；勾股定理；三角形中位线定理；矩形的判定与性质；平行线分线段成比例；相似三角形的判定与性质；锐角三角函数的定义；特殊角的三角函数值．菁优网版权所有专题：综合题．分析：（1）①连接DM、MC，如图1，易证四边形OCMD是矩形，从而得到M D∥OA，MC∥OB，由点M是AB的中点即可得到BD=DO，AC=OC，然后利用点M的坐标就可解决问题； ②根据勾股定理可求出AB的长，从而得到BM的长，要求ME的长，只需求BE的长，只需证△OBM∽△EBD，然后运用相似三角形的性质即可；（2）连接DP、PE，如图2，由 =3可得OK=3MK，进而得到OM=4MK ，PM=2MK，PK=MK．易证△DPK≌△EMK，则有DK=EK．由PD=PE可得PK⊥DE，从而可得cos∠DPK= =，则有∠DPK=60°，根据圆周角定理可得∠DOM=30°．由∠AOB=90°，AM=BM可得OM=BM，即可得到∠O BA=∠DOM=30°；（3）连接PD、OE，如图3，设MK=t，则有OK=yt，OM=（y+1）t，BM 40 =OM=（y+1）t，DP=PM= ，PK= ．由DP∥BM可得△ t，从而可求得OE= DKP∽△EKM，则有 =，由此可得ME= •，BE= ，则有x=tan∠OBA= =，即x2= =1﹣ ，整理得y= ．解答：解：（1）①连接DM、MC，如图1． ∵OM是⊙P的直径， ∴∠MDO=∠MCO=90°． ∵∠AOB=90°， ∴四边形OCMD是矩形， ∴MD∥OA，MC∥OB， ∴=，=．∵点M是AB的中点，即BM=AM， ∴BD=DO，AC=OC． ∵点M的坐标为（3，4）， ∴OB=2OD=8，OA=2OC=6， ∴点B的坐标为（0，8），点A的坐标为（6，0）； ②在Rt△AOB中，OA=6，OB=8， ∴AB= =10． ∴BM= AB=5． ∵∠OBM=∠EBD，∠BOM=∠BED， ∴△OBM∽△EBD， ∴=，∴ = ，41 ∴BE= ，∴ME=BE﹣BM= ﹣5= ；（2）连接DP、PE，如图2． ∵=3， ∴OK=3MK， ∴OM=4MK，PM=2MK， ∴PK=MK． ∵OD=BD，OP=MP， ∴DP∥BM， ∴∠PDK=∠MEK，∠DPK=∠EMK．在△DPK和△EMK中，，∴△DPK≌△EMK， ∴DK=EK． ∵PD=PE， ∴PK⊥DE， ∴cos∠DPK= =， ∴∠DPK=60°， ∴∠DOM=30°． ∵∠AOB=90°，AM=BM， ∴OM=BM， ∴∠OBA=∠DOM=30°；（3）y关于x的函数解析式为y= ．42 提示：连接PD、OE，如图3．设MK=t，则有OK=yt，OM=（y+1）t， BM=OM=（y+1）t，DP=PM= PK= ﹣t= ，．由DP∥BM可得△DKP∽△EKM，则有，可得ME= t． =∵OM是⊙P的直径， ∴∠OEM=90°， ∴OE2=OM2﹣ME2=[（y+1）t]2﹣[ t]2= •（y2﹣2y），即OE= •，BE=BM+ME=（y+1）t+ t= ，∴x=tan∠OBA= =，∴x2= =1﹣ ，整理得：y= ．43 点评：本题主要考查了圆周角定理、相似三角形的判定与性质、全等三角形的判定与性质、矩形的判定与性质、平行线分线段成比例、三角形中位线定理、直角三角形斜边上的中线等于斜边的一半、等腰三角形的性质、勾股定理、三角函数的定义、特殊角的三角函数值等知识，综合性比较强，有一定的难度，通过证明△OBM∽△EBD求出BE是解决第（1）② 小题的关键，通过证明△DPK≌△EMK得到DK=EK是解决第（2）小题的关键，设MK=t，然后运用相似三角形的性质、勾股定理求出OE、BE（用y、t的代数式表示）是解决第（3）小题的关键．　44