2015年宁夏省中考数学试卷（含解析版）

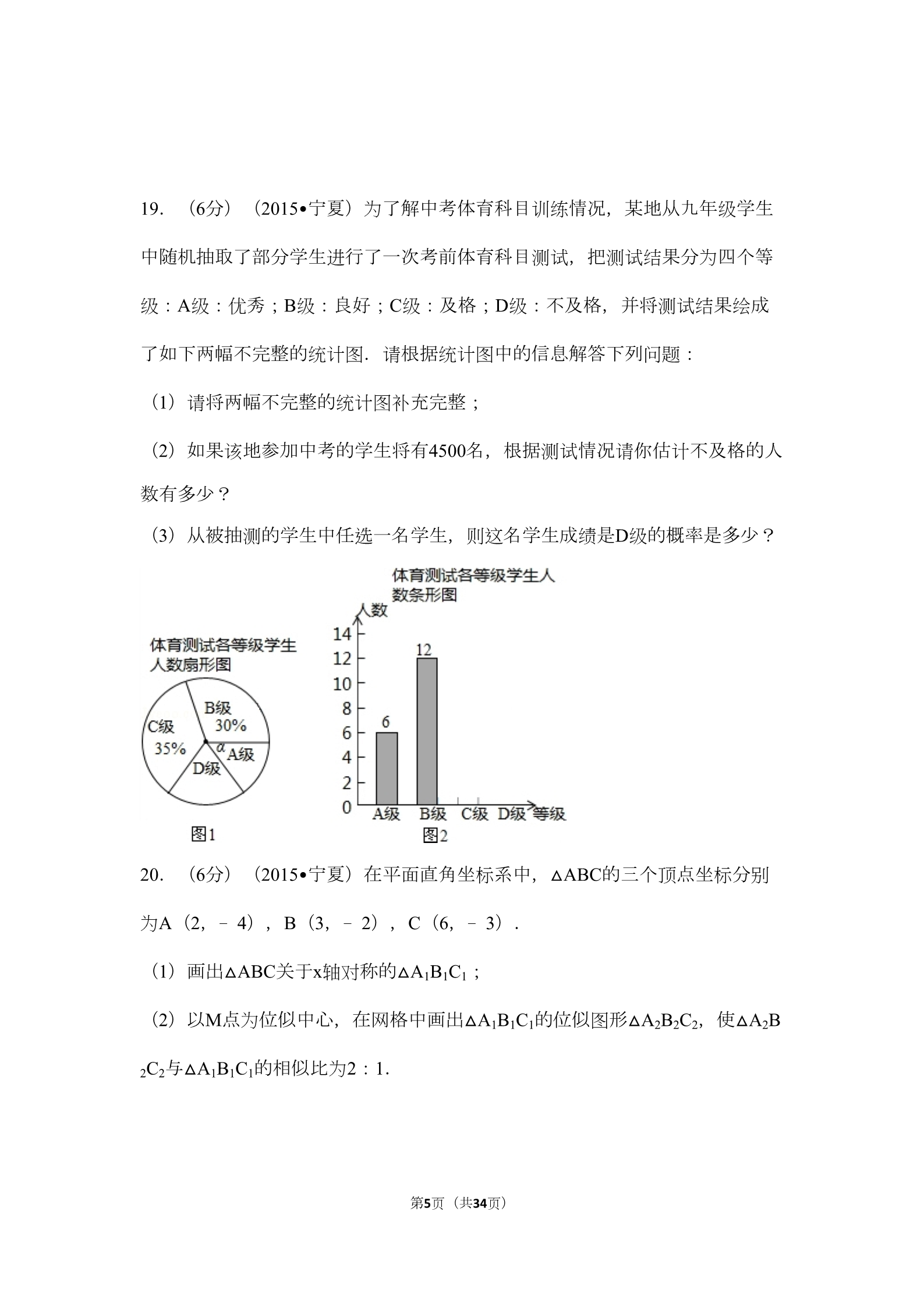
2015年宁夏中考数学试卷一、选择题（下列每小题所给的四个答案中只有一个是正确的，每小题3分，共24分） 1．（3分）（2015•宁夏）下列计算正确的是（　　））﹣1= （﹣1）2=2 　A B=2 CD（．．．．2．（3分）（2015•宁夏）生物学家发现了一种病毒的长度约为0.00000432毫米．数据0.00000432用科学记数法表示为（　　） 0.432×10﹣5 4.32×10﹣6 4.32×10﹣7 43.2×10﹣7 　A BCD．．．．3．（3分）（2015•宁夏）如图，放置的一个机器零件（图1），若其主视图如（图2）所示，则其俯视图为（　　）　A BCD．．．．4．（3分）（2015•宁夏）某校10名学生参加“心理健康”知识测试，他们得分情况如下表：人数分数 234180 85 90 95 那么这10名学生所得分数的众数和中位数分别是（　　）　A 95和85 B 90和85 C 90和87.5 D 85和87.5 ．．．．5．（3分）（2015•宁夏）关于x的一元二次方程x2+x+m=0有实数根，则m的取值范围是（　　）第1页（共34页）　A BCDm≥ m≤ m≥ m≤ ．．．．6．（3分）（2015•宁夏）如图，四边形ABCD是⊙O的内接四边形，若∠BOD= 88°，则∠BCD的度数是（　　） 88° 92° 106° 136° 　A BCD．．．．7．（3分）（2015•宁夏）如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60米2，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于 x的方程是（　　） x2+9x﹣8=0 x2﹣9x﹣8=0 x2﹣9x+8=0 2×2﹣9x+8=0 　A BCD．．．．8．（3分）（2015•宁夏）函数y= 与y=﹣kx2+k（k≠0）在同一直角坐标系中的图象可能是（　　）　A BCD．．．．　二、填空题（每小题3分，共24分）第2页（共34页） 9．（3分）（2015•宁夏）因式分解：x3﹣xy2=　　　　　　． 10．（3分）（2015•宁夏）从2，3，4这三个数字中，任意抽取两个不同数字组成一个两位数，则这个两位数能被3整除的概率是　　　　　　． 11．（3分）（2015•宁夏）如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若A点的坐标为（﹣1，0），则点C的坐标为　　　　　　．12．（3分）（2015•宁夏）已知扇形的圆心角为120°，所对的弧长为扇形的面积是　　　　　　．，则此 13．（3分）（2015•宁夏）如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E ，连接BC．若AB=2 ，∠BCD=30°，则⊙O的半径为　　　　　　． 14．（3分）（2015•宁夏）如图，在平面直角坐标系中，点A的坐标为（0，4 ），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线y= x上一点，则点B与其对应点B′间的距离为　　　　　　．第3页（共34页） 15．（3分）（2015•宁夏）如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，则C E的长为　　　　　　． 16．（3分）（2015•宁夏）如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为　　　　　　．　三、解答题（每题6分，共36分） 17．（6分）（2015•宁夏）解方程： =1．　18．（6分）（2015•宁夏）解不等式组．第4页（共34页）　19．（6分）（2015•宁夏）为了解中考体育科目训练情况，某地从九年级学生中随机抽取了部分学生进行了一次考前体育科目测试，把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格，并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：（1）请将两幅不完整的统计图补充完整；（2）如果该地参加中考的学生将有4500名，根据测试情况请你估计不及格的人数有多少？（3）从被抽测的学生中任选一名学生，则这名学生成绩是D级的概率是多少？ 20．（6分）（2015•宁夏）在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣4），B（3，﹣2），C（6，﹣3）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B 2C2与△A1B1C1的相似比为2：1．第5页（共34页）　21．（6分）（2015•宁夏）在平行四边形ABCD中，E为BC边上的一点．连结A E．（1）若AB=AE，求证：∠DAE=∠D；（2）若点E为BC的中点，连接BD，交AE于F，求EF：FA的值．　22．（6分）（2015•宁夏）某校在开展“校园献爱心”活动中，准备向南部山区学校捐赠男、女两种款式的书包．已知男款书包的单价50元/个，女款书包的单价70元/个．第6页（共34页）（1）原计划募捐3400元，购买两种款式的书包共60个，那么这两种款式的书包各买多少个？（2）在捐款活动中，由于学生捐款的积极性高涨，实际共捐款4800元，如果至少购买两种款式的书包共80个，那么女款书包最多能买多少个？　　四、解答题（23题、24题每题8分，25题、26题每题10分，共36分） 23．（8分）（2015•宁夏）如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O 外一点，连接PB、AB，∠PBA=∠C．（1）求证：PB是⊙O的切线；（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为2 ，求BC的长．　第7页（共34页） 24．（8分）（2015•宁夏）已知点A（，3）在抛物线y=﹣ 上，设点A关于抛物线对称轴对称的点为B．（1）求点B的坐标； x的图象（2）求∠AOB度数．　25．（10分）（2015•宁夏）某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计，得到如下数据：30 40 34 32 38 24 40 20 42 16 单价（元/件）销量（件）（1）计算这5天销售额的平均数（销售额=单价×销量）；（2）通过对上面表格中的数据进行分析，发现销量y（件）与单价x（元/件）之间存在一次函数关系，求y关于x的函数关系式（不需要写出函数自变量的取值范围）；（3）预计在今后的销售中，销量与单价仍然存在（2）中的关系，且该产品的成本是20元/件．为使工厂获得最大利润，该产品的单价应定为多少？　第8页（共34页） 26．（10分）（2015•宁夏）如图，是一副学生用的三角板，在△ABC 中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45° ，且A1B1=CB．若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1 C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边A B的交点为M，设AC=a．（1）计算A1C1的长；（2）当α=30°时，证明：B1C1∥AB；（3）若a= ，当α=45°时，计算两个三角板重叠部分图形的面积；（4）当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积．（参考数据：sin15°= ，cos15°= ，tan15°=2﹣ ，sin75°= ，cos75°= ，tan75°=2+ ）　　第9页（共34页） 2015年宁夏中考数学试卷参考答案与试题解析　一、选择题（下列每小题所给的四个答案中只有一个是正确的，每小题3分，共24分） 1．（3分）（2015•宁夏）下列计算正确的是（　　） ﹣1 （）=（D． ﹣1）2=2 　A． B． C． =2 二次根式的混合运算；负整数指数幂．菁优网版权所有计算题．考点：专题：根据二次根式的加减法对A进行判断；根据二次根式的除法法则对B进行判断；根据负整数整数幂对B进行判断；根据完全平方公式对D进行判断．分析：解：与不能合并，所以A选项错误； =2，所以B选项正确；解答：B、原式= C、原式= =，所以C选项正确； D、原式=3﹣2 +1=4﹣2 ，所以D选项正确．故选B．点评本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．也考查了负整数整数幂．：　2．（3分）（2015•宁夏）生物学家发现了一种病毒的长度约为0.00000432毫米．数据0.000 00432用科学记数法表示为（　　） 0.432×10﹣5 4.32×10﹣6 4.32×10﹣7 43.2×10﹣7 D．　A． B． C．科学记数法—表示较小的数．菁优网版权所有考点：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科分析第10页（共34页）学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．：解：0.00000432=4.32×10﹣6 故选：B．，解答：点评本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．：　3．（3分）（2015•宁夏）如图，放置的一个机器零件（图1），若其主视图如（图2）所示，则其俯视图为（　　）　A． B． C． D．简单组合体的三视图．菁优网版权所有考点：俯视图是从上面看所得到的图形，此几何体从上面看可以看到一个长方形，中间有一个长方形．分析：解答：解：其俯视图为故选：D．．点评此题主要考查了画三视图，关键是掌握俯视图所看的位置，注意要把所看到的棱都要用实线画出来．：　4．（3分）（2015•宁夏）某校10名学生参加“心理健康”知识测试，他们得分情况如下表：人数分数 234180 85 90 95 那么这10名学生所得分数的众数和中位数分别是（　　）　A．95和85 B．90和85 C．90和87.5 D．85和87.5 第11页（共34页）众数；中位数．菁优网版权所有考点：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，可得答案．解：在这一组数据中9是出现次数最多的，故众数是90；分析：解答：排序后处于中间位置的那个数是85，90，那么由中位数的定义可知，这组数据的中位数是 =87.5；故选：C．点评本题为统计题，考查极差、众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数），叫做这组数据的中位数．如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．：　5．（3分）（2015•宁夏）关于x的一元二次方程x2+x+m=0有实数根，则m的取值范围是（　　）　A． B． C． D． m≥ m≤ m≥ m≤ 根的判别式．菁优网版权所有考点：方程有实数根，则△≥0，建立关于m的不等式，求出m的取值范围．分析：解：由题意知，△=1﹣4m≥0， ∴m≤ ，解答：故选D．点评本题考查了根的判别式，总结：1、一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；：第12页（共34页）（3）△＜0⇔方程没有实数根．　6．（3分）（2015•宁夏）如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，则∠B CD的度数是（　　） 88° 92° 106° 136° D．　A． B． C．圆内接四边形的性质；圆周角定理．菁优网版权所有考点：首先根据∠BOD=88°，应用圆周角定理，求出∠BAD的度数多少；然后根据圆内接四边形的性质，可得∠BAD+∠BCD=180°，据此求出∠BCD的度数是多少即可．分析：解答解：∵∠BOD=88°，：∴∠BAD=88°÷2=44°， ∵∠BAD+∠BCD=180°， ∴∠BCD=180°﹣44°=136°，即∠BCD的度数是136°．故选：D．点评（1）此题主要考查了圆内接四边形的性质和应用，要熟练掌握，解答此题的关键是要明确：①圆内接四边形的对角互补．②圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．：（2）此题还考查了圆周角定理的应用，要熟练掌握，解答此题的关键是要明确：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．　第13页（共34页） 7．（3分）（2015•宁夏）如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60米2，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于x的方程是（　　） x2+9x﹣8=0 x2﹣9x﹣8=0 x2﹣9x+8=0 2×2﹣9x+8=0 D．　A． B． C．由实际问题抽象出一元二次方程．菁优网版权所有几何图形问题．考点：专题：设人行道的宽度为x米，根据矩形绿地的面积之和为60米2，列出一元二次方程．分析：解：设人行道的宽度为x米，根据题意得，（18﹣3x）（6﹣2x）=60，化简整理得，x2﹣9x+8=0．故选C．解答：点评本题考查了由实际问题抽象出一元二次方程，利用两块相同的矩形绿地面积之和为6 0米2得出等式是解题关键．：　8．（3分）（2015•宁夏）函数y= 与y=﹣kx2+k（k≠0）在同一直角坐标系中的图象可能是（　　）　A． B． C． D．二次函数的图象；反比例函数的图象．菁优网版权所有考点第14页（共34页）：专题压轴题；数形结合．：本题可先由反比例函数的图象得到字母系数的正负，再与二次函数的图象相比较看是否一致．分析：解：由解析式y=﹣kx2+k可得：抛物线对称轴x=0；解答：A、由双曲线的两支分别位于二、四象限，可得k＜0，则﹣k＞0，抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上；本图象与k的取值相矛盾，故A错误； B、由双曲线的两支分别位于一、三象限，可得k＞0，则﹣k＜0，抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上，本图象符合题意，故B正确； C、由双曲线的两支分别位于一、三象限，可得k＞0，则﹣k＜0，抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上，本图象与k的取值相矛盾，故C错误； D、由双曲线的两支分别位于一、三象限，可得k＞0，则﹣k＜0，抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上，本图象与k的取值相矛盾，故D错误．故选：B．点评本题主要考查了二次函数及反比例函数和图象，解决此类问题步骤一般为：（1）先根据图象的特点判断k取值是否矛盾；（2）根据二次函数图象判断抛物线与y轴的交：点是否符合要求．　二、填空题（每小题3分，共24分） 9．（3分）（2015•宁夏）因式分解：x3﹣xy2=　x（x﹣y）（x+y）　．提公因式法与公式法的综合运用．菁优网版权所有考点：先提取公因式x，再对余下的多项式利用平方差公式继续分解．分析：解：x3﹣xy2 解答：=x（x2﹣y2） =x（x﹣y）（x+y）．第15页（共34页）故答案为：x（x﹣y）（x+y）．点评本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止：．　10．（3分）（2015•宁夏）从2，3，4这三个数字中，任意抽取两个不同数字组成一个两位数，则这个两位数能被3整除的概率是　．列表法与树状图法．菁优网版权所有考点：根据所抽取的数据拼成两位数，得出总数及能被3整除的数，求概率．分析：解：如下表，任意抽取两个不同数字组成一个两位数，共6种情况，其中能被3整除的有24，42两种，解答：∴组成两位数能被3整除的概率为= = ．故答案为：．点评本题考查了求概率的方法：列表法和树状图法．关键是通过画表格（图）求出组成：　两位数的所有可能情况及符合条件的几种可能情况． 11．（3分）（2015•宁夏）如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若A点的坐标为（﹣1，0），则点C的坐标为　（，﹣ ）　．第16页（共34页）正多边形和圆；坐标与图形性质．菁优网版权所有计算题．考点：专题：先连接OE，由于正六边形是轴对称图形，并设EF交Y轴于G，那么∠GOE=30°；在Rt △GOE中，则GE= ，OG= ．即可求得E的坐标，和E关于Y轴对称的F点的坐标，分析：其他坐标类似可求出．解：连接OE，由正六边形是轴对称图形知：在Rt△OEG中，∠GOE=30°，OE=1．解答：∴GE= ，OG= ．∴A（﹣1，0），B（﹣ ，﹣ ），C（，﹣ ）D（1，0），E（，），F （﹣ ，）．故答案为：（，﹣ ）点评本题利用了正六边形的对称性，直角三角形30°的角所对的边等于斜边的一半，勾股定理等知识．：　12．（3分）（2015•宁夏）已知扇形的圆心角为120°，所对的弧长为积是　．，则此扇形的面第17页（共34页）扇形面积的计算；弧长的计算．菁优网版权所有计算题．考点：专题：利用弧长公式列出关系式，把圆心角与弧长代入求出扇形的半径，即可确定出扇形的面积．分析：解答：解：∵扇形的圆心角为120°，所对的弧长为，∴l= =，解得：R=4，则扇形面积为 Rl= 故答案为：，点评此题考查了扇形面积的计算，以及弧长公式，熟练掌握公式是解本题的关键．：　13．（3分）（2015•宁夏）如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC．若AB=2 ，∠BCD=30°，则⊙O的半径为　　．垂径定理；勾股定理；圆周角定理．菁优网版权所有考点：连接OB，根据垂径定理求出BE，求出∠BOE=60°，解直角三角形求出OB即可．分析：第18页（共34页）解答：解：连接OB， ∵OC=OB，∠BCD=30°， ∴∠BCD=∠CBO=30°， ∴∠BOE=∠BCD+∠CBO=60°， ∵直径CD⊥弦AB，AB=2 ∴BE= AB=，∠OEB=90°， ∴OB= ，=，即⊙O的半径为故答案为：，．点评本题考查了垂径定理，等腰三角形的性质，解直角三角形，三角形外角性质的应用，能根据垂径定理求出BE和解直角三角形求出OB长是解此题的关键，难度适中．：　14．（3分）（2015•宁夏）如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB 沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线y= x上一点，则点B与其对应点B′间的距离为　5　．一次函数图象上点的坐标特征；坐标与图形变化-平移．菁优网版权所有考点：第19页（共34页）根据平移的性质知BB′=AA′．由一次函数图象上点的坐标特征可以求得点A′的坐标，所以根据两点间的距离公式可以求得线段AA′的长度，即BB′的长度．解：如图，连接AA′、BB′．分析：解答：∵点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′， ∴点A′的纵坐标是4．又∵点A的对应点在直线y= x上一点， ∴4= x，解得x=5． ∴点A′的坐标是（5，4）， ∴AA′=5． ∴根据平移的性质知BB′=AA′=5．故答案为：5．点评本题考查了一次函数图象上点的坐标特征、坐标与图形变化﹣﹣平移．根据平移的性质得到BB′=AA′是解题的关键．：　15．（3分）（2015•宁夏）如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，则CE的长为　．翻折变换（折叠问题）．菁优网版权所有考点：设CE=x，由矩形的性质得出AD=BC=5，CD=AB=3，∠A=∠D=90°．由折叠的性质得分析第20页（共34页）出BF=BC=5，EF=CE=x，DE=CD﹣CE=3﹣x．在Rt△ABF中利用勾股定理求出AF的：长度，进而求出DF的长度；然后在Rt△DEF根据勾股定理列出关于x的方程即可解决问题．解：设CE=x．解答：∵四边形ABCD是矩形， ∴AD=BC=5，CD=AB=3，∠A=∠D=90°． ∵将△BCE沿BE折叠，使点C恰好落在AD边上的点F处， ∴BF=BC=5，EF=CE=x，DE=CD﹣CE=3﹣x．在Rt△ABF中，由勾股定理得： AF2=52﹣32=16， ∴AF=4，DF=5﹣4=1．在Rt△DEF中，由勾股定理得： EF2=DE2+DF2，即x2=（3﹣x）2+12，解得：x= ，故答案为．点评本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理、矩形的性质、方程思想等知识，关键是熟练掌握勾股定理，找准对应边．：　16．（3分）（2015•宁夏）如图，港口A在观测站O的正东方向，OA=4km，某船从港口A 出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东6 0°的方向，则该船航行的距离（即AB的长）为　2 km　．第21页（共34页）解直角三角形的应用-方向角问题．菁优网版权所有考点：分析：过点A作AD⊥OB于D．先解Rt△AOD，得出AD= OA=2km，再由△ABD是等腰直角三角形，得出BD=AD=2km，则AB= AD=2 km．解：如图，过点A作AD⊥OB于D．解答：在Rt△AOD中，∵∠ADO=90°，∠AOD=30°，OA=4km， ∴AD= OA=2km．在Rt△ABD中，∵∠ADB=90°，∠B=∠CAB﹣∠AOB=75°﹣30°=45°， ∴BD=AD=2km， ∴AB= AD=2 km．即该船航行的距离（即AB的长）为2 km．故答案为2 km．点评本题考查了解直角三角形的应用﹣方向角问题，难度适中，作出辅助线构造直角三角形是解题的关键．：　三、解答题（每题6分，共36分） 17．（6分）（2015•宁夏）解方程： =1．解分式方程．菁优网版权所有考点：因为x2﹣1=（x+1）（x﹣1），所以可确定最简公分母（x+1）（x﹣1），然后方程两边同乘最简公分母将分式方程转化为整式方程求解即可，注意检验．解：方程两边同乘（x+1）（x﹣1），分析：解答第22页（共34页）得x（x+1）﹣（2x﹣1）=（x+1）（x﹣1），解得x=1．：经检验x=1是增根，原方程无解．点评本题考查了解分式方程，解分式方程要注意：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．（3）去分母时要注意符号的变化．：　18．（6分）（2015•宁夏）解不等式组．解一元一次不等式组．菁优网版权所有考点：先解不等式组中每一个不等式的解集，再利用求不等式组解集的口诀“大小小大中间找”即可确定结果．分析：解答：解：由①得：x≥2，由②得：x＜4，所以这个不等式组的解集为：2≤x＜4．点评本题主要考查了一元一次不等式组解集的求法，其简便方法就是利用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小解不了（：无解集）．　19．（6分）（2015•宁夏）为了解中考体育科目训练情况，某地从九年级学生中随机抽取了部分学生进行了一次考前体育科目测试，把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格，并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：（1）请将两幅不完整的统计图补充完整；（2）如果该地参加中考的学生将有4500名，根据测试情况请你估计不及格的人数有多少？第23页（共34页）（3）从被抽测的学生中任选一名学生，则这名学生成绩是D级的概率是多少？条形统计图；用样本估计总体；扇形统计图；概率公式．菁优网版权所有考点：（1）首先根据题意求得总人数，继而求得A级与D级占的百分比，求得C级与D级的人数；则可补全统计图；分析：（2）根据题意可得：估计不及格的人数有：4500×20%=900（人）；（3）由概率公式的定义，即可求得这名学生成绩是D级的概率．解：（1）总人数为：12÷30%=40（人），解答：A级占： ×100%=15%，D级占：1﹣35%﹣30%﹣15%=20%； C级人数：40×35%=14（人），D级人数：40×20%=8（人），补全统计图得：第24页（共34页）（2）估计不及格的人数有：4500×20%=900（人）；（3）从被抽测的学生中任选一名学生，则这名学生成绩是D级的概率是：20%．点评此题考查了概率公式的应用以及扇形统计图与条形统计图的知识．用到的知识点为：概率=所求情况数与总情况数之比．：　20．（6分）（2015•宁夏）在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣4 ），B（3，﹣2），C（6，﹣3）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1 C1的相似比为2：1．作图-位似变换；作图-轴对称变换．菁优网版权所有考点：（1）利用轴对称图形的性质进而得出对应点位置进而画出图形即可；（2）利用位似图形的性质得出对应点位置进而画出图形即可．解：（1）如图所示：△A1B1C1，即为所求；分析：解答：（2）如图所示：△A2B2C2，即为所求．第25页（共34页）点评此题主要考查了轴对称变换以及位似变换，根据题意得出对应点位置是解题关键．：　21．（6分）（2015•宁夏）在平行四边形ABCD中，E为BC边上的一点．连结AE．（1）若AB=AE，求证：∠DAE=∠D；（2）若点E为BC的中点，连接BD，交AE于F，求EF：FA的值．相似三角形的判定与性质；平行四边形的性质．菁优网版权所有考点：（1）根据平行四边形的对边互相平行可得AD∥BC，再根据两直线平行，内错角相等可得∠AEB=∠EAD，根据等边对等角可得∠ABE=∠AEB，即可得证；（2）由四边形ABCD是平行四边形，可证得△BEF∽△AFD，即可求得EF：FA的值．证明：（1）在平行四边形ABCD中，AD∥BC，分析：解答：∴∠AEB=∠EAD， ∵AE=AB，第26页（共34页） ∴∠ABE=∠AEB， ∴∠B=∠EAD， ∵∠B=∠D， ∴∠DAE=∠D；（2）∵四边形ABCD是平行四边形， ∴AD∥BC，AD=BC， ∴△BEF∽△AFD， ∴，∵E为BC的中点， ∴BE= BC= AD， ∴EF：FA=1：2．点评此题考查了相似三角形的判定与性质与平行四边形的性质．熟练掌握平行四边形的性质是解题的关键．：　22．（6分）（2015•宁夏）某校在开展“校园献爱心”活动中，准备向南部山区学校捐赠男、女两种款式的书包．已知男款书包的单价50元/个，女款书包的单价70元/个．（1）原计划募捐3400元，购买两种款式的书包共60个，那么这两种款式的书包各买多少个？（2）在捐款活动中，由于学生捐款的积极性高涨，实际共捐款4800元，如果至少购买两种款式的书包共80个，那么女款书包最多能买多少个？一元一次不等式的应用；二元一次方程组的应用．菁优网版权所有考点：（1）设原计划买男款书包x个，则女款书包（60﹣x）个，根据题意得：50x+70（60 分析：﹣x）=3400，即可解答；第27页（共34页）（2）设女款书包最多能买y个，则男款书包（80﹣y）个，根据题意得：70y+50（80 ﹣y）≤4800，即可解答．解：（1）设原计划买男款书包x个，则女款书包（60﹣x）个，根据题意得：50x+70（60﹣x）=3400，解得：x=40，解答：60﹣x=60﹣40=20，答：原计划买男款书包40个，则女款书包20个．（2）设女款书包最多能买y个，则男款书包（80﹣y）个，根据题意得：70y+50（80﹣y）≤4800，解得：y≤40， ∴女款书包最多能买40个．点评本题考查了一元一次方程、一元一次不等式的应用，解决本题的关键是根据题意列：　出方程和不等式．四、解答题（23题、24题每题8分，25题、26题每题10分，共36分） 23．（8分）（2015•宁夏）如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA=∠C．（1）求证：PB是⊙O的切线；（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为2 ，求BC的长．切线的判定．菁优网版权所有考点：连接OB，由圆周角定理得出∠ABC=90°，得出∠C+∠BAC=90°，再由OA=OB，得出∠ BAC=∠OBA，证出∠PBA+∠OBA=90°，即可得出结论；分析：（2）证明△ABC∽△PBO，得出对应边成比例，即可求出BC的长．第28页（共34页）（1）证明：连接OB，如图所示： ∵AC是⊙O的直径， ∴∠ABC=90°，解答：∴∠C+∠BAC=90°， ∵OA=OB， ∴∠BAC=∠OBA， ∵∠PBA=∠C， ∴∠PBA+∠OBA=90°，即PB⊥OB， ∴PB是⊙O的切线；（2）解：∵⊙O的半径为2 ，∴OB=2 ，AC=4 ∵OP∥BC，，∴∠C=∠BOP，又∵∠ABC=∠PBO=90°， ∴△ABC∽△PBO， ∴，即，∴BC=8．点评本题考查了切线的判定、圆周角定理、平行线的性质、相似三角形的判定与性质；熟练掌握圆周角定理、切线的判定是解决问题的关键．：　24．（8分）（2015•宁夏）已知点A（，3）在抛物线y=﹣ x的图象上，设点 A关于抛物线对称轴对称的点为B．第29页（共34页）（1）求点B的坐标；（2）求∠AOB度数．二次函数图象上点的坐标特征；二次函数的性质．菁优网版权所有考点：（1）首先求得抛物线的对称轴，然后确定点A关于对称轴的交点坐标即可；（2）根据确定的两点的坐标确定∠AOC和∠BOC的度数，从而确定∠AOB的度数．分析：x=﹣ （x﹣2 ）2+4，解答：解：（1）∵y=﹣ ∴对称轴为x=2 ，∴点A（，3）关于x=2 的对称点的坐标为（3 ，3）；（2）如图： ∵A（，3）、（3 ，3）， ∴BC=3 ，AC= ，OC=3， ∴tan∠AOC= =，tan∠BOC= ==，∴∠AOC=30°，∠BOC=60°， ∴∠AOB=30°．点评本题考查了二次函数图象上的点的坐标及二次函数的性质，能够确定抛物线的对称轴是解答本题的关键，难度不大．：　25．（10分）（2015•宁夏）某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计，得到如下数据：单价（元/件） 30 34 38 40 42 第30页（共34页）销量（件）（1）计算这5天销售额的平均数（销售额=单价×销量）； 40 32 24 20 16 （2）通过对上面表格中的数据进行分析，发现销量y（件）与单价x（元/件）之间存在一次函数关系，求y关于x的函数关系式（不需要写出函数自变量的取值范围）；（3）预计在今后的销售中，销量与单价仍然存在（2）中的关系，且该产品的成本是20元/ 件．为使工厂获得最大利润，该产品的单价应定为多少？二次函数的应用．菁优网版权所有应用题．考点：专题：（1）根据题中表格中的数据列出算式，计算即可得到结果；（2）设y=kx+b，从表格中找出两对值代入求出k与b的值，即可确定出解析式；（3）设定价为x元时，工厂获得的利润为W，列出W与x的二次函数解析式，利用二次函数性质求出W最大时x的值即可．分析：解答：解：（1）根据题意得： =934.4（元）；（2）根据题意设y=kx+b，把（30，40）与（40，20）代入得：，解得：k=﹣2，b=100，则y=﹣2x+100；（3）设定价为x元时，工厂获得的利润为W，根据题意得：W=（x﹣20）y=（x﹣20）（﹣2x+100）=﹣2×2+140x﹣2000=﹣2（x﹣ 35）2+450， ∵当x=35时，W最大值为450，则为使工厂获得最大利润，该产品的单价应定为35元．点评此题考查了二次函数的应用，待定系数法确定一次函数解析式，以及二次函数的性质，熟练掌握二次函数性质是解本题的关键．：　第31页（共34页） 26．（10分）（2015•宁夏）如图，是一副学生用的三角板，在△ABC 中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45°，且A1B1=C B．若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为M，设AC=a．（1）计算A1C1的长；（2）当α=30°时，证明：B1C1∥AB；（3）若a= ，当α=45°时，计算两个三角板重叠部分图形的面积；（4）当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积．（参考数据：sin15°= ，cos15°= ，tan15°=2﹣ ，sin75°= ，cos75° =，tan75°=2+ ）几何变换综合题．菁优网版权所有创新题型．考点：专题：（1）在Rt△ABC中，由特殊锐角三角函数值，先求得BC的长，然后在Rt△A1B1C1中利用特殊锐角三角函数即可求得A1C1的长；分析：（2）利用三角形的外角的性质求得∠BMC=90°，然后利用同位角相等，两直线平行进行判定即可；（3）两个三角板重叠部分图形的面积=△A1B1C1的面积﹣△BC1M的面积；（4）两个三角板重叠部分图形的面积=△CC1B1的面积﹣三角形FB1C的面积﹣三角形 DC1M的面积．解答解：（1）在Rt△ABC中，∠B=30°，AC=a，第32页（共34页）：由特殊锐角三角函数可知：，∴BC= ．∴B1C= 在Rt△A1B1C1，∠B1=∠45°， ∴．∴A1C1= =．（2）∵∠ACM=30°，∠A=60°， ∴∠BMC=90°． ∴∠C1=∠BMC． ∴B1C1∥AB．（3）如下图：由（1）可知：A1C1= ∴△A1B1C1的面积= ==3+ =∵∠A1B1C1=45°，∠ABC=30° ∴∠MBC1=15° 在Rt△BC1M中，C1M=BCtan15°=（3+ ）（2﹣ ）=3﹣ ∴Rt△BC1M的面积= ，==3． ∴两个三角板重叠部分图形的面积=△A1B1C1的面积﹣△BC1M的面积=3 +3．（4）如下图：过点B1作B1E⊥BC，垂足为E．第33页（共34页）由（1）可知：BC= ，A1C1= ，∵∠MCA=60°，∠A=60°， ∴∠AMC=60° ∴MC=AC=MA=a． ∴C1M=C1A1﹣MC= ．∵∠MCA=60°， ∴∠C1A1B=30°， ∴∠C1MD=∠B+∠C1A1B=60° 在Rt△DC1M中，由特殊锐角三角函数可知：DC1=C1M•tan60°= ∴三角形DC1M的面积= C1M•DC1= a2，在Rt△BB1C中，C1B=BC= ，∠BCB1=15°，由特殊锐角三角函数可知：B1E=C1B• sin15°= a，，在Rt△FC1C中，C1C= ，∠CC1F=30°，由特殊锐角三角函数可知：CF=CC1÷ =．∴三角形FB1C的面积= =．两个三角板重叠部分图形的面积=△A1C1B1的面积﹣三角形FB1C的面积﹣三角形DC1 M的面积= 点评本题主要考查的是锐角三角函数和三角形的综合应用，难度较大，解答本题的关键．是灵活应用锐角函数求得相关线段的长度．：　第34页（共34页）