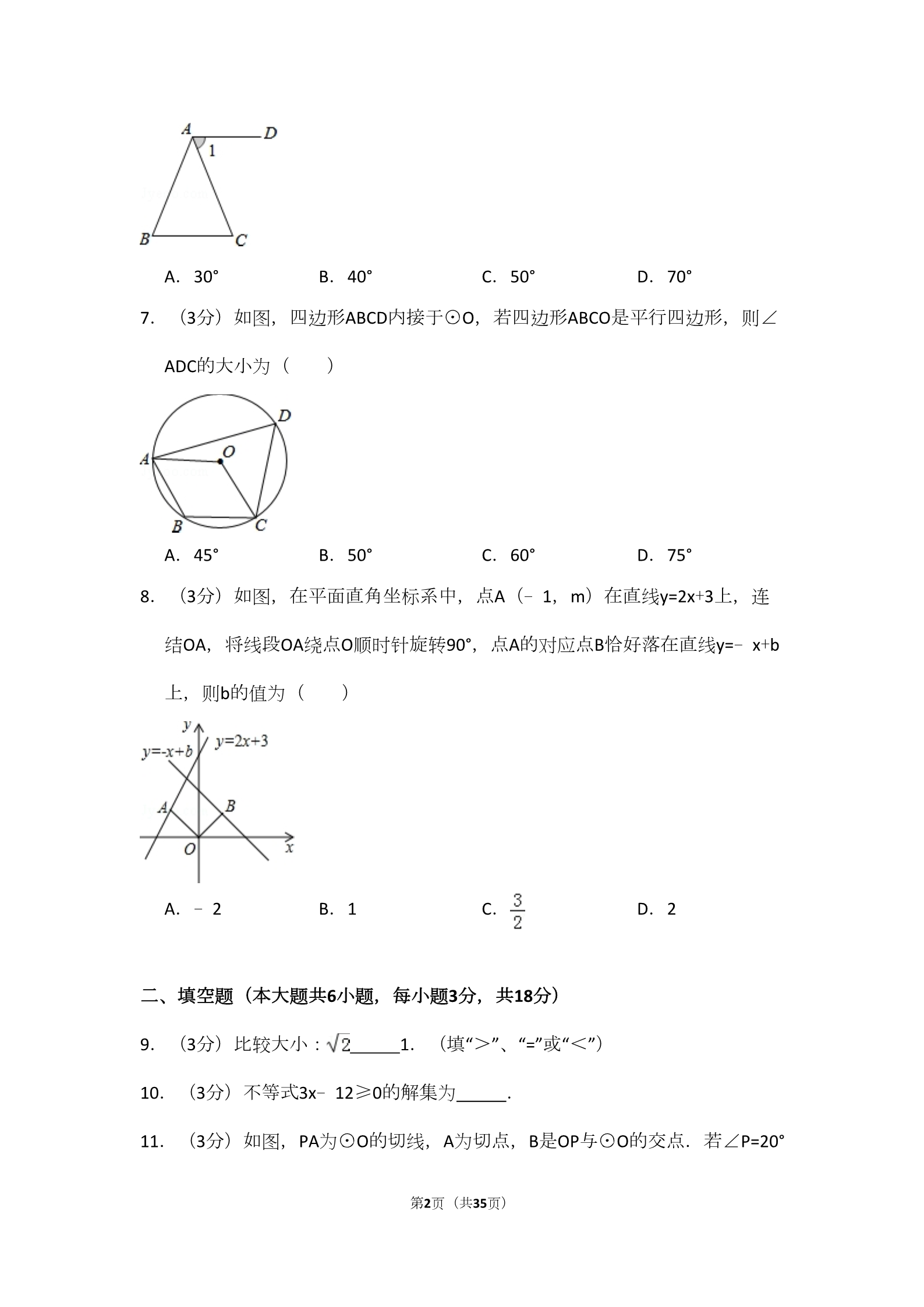
2015年吉林省长春市中考数学试卷（含解析版）

2015年吉林省长春市中考数学试卷一、选择题（本大题共8小题，每小题3分，共24分） 1．（3分）﹣3的绝对值是（　　） A．3 B．﹣3 C． D． 2．（3分）在长春市“暖房子工程”实施过程中，某工程队做了面积为632000m2 的外墙保暖．632000这个数用科学记数法表示为（　　） A．63.2×104 3．（3分）计算（a2）3的结果是（　　） A．3a2 B．a5 B．6.32×105 C．0.632×106 D．0.632×106 C．a6 D．a3 4．（3分）图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（　　） A．主视图相同 B．俯视图相同 C．左视图相同 D．主视图、俯视图、左视图都相同 5．（3分）方程x2﹣2x+3=0的根的情况是（　　） A．有两个相等的实数根 C．没有实数根 B．只有一个实数根 D．有两个不相等的实数根 6．（3分）如图，在△ABC中，AB=AC，过点A作AD∥BC．若∠1=70°，则∠BAC 的大小为（　　）第1页（共35页） A．30° B．40° C．50° D．70° 7．（3分）如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ ADC的大小为（　　） A．45° B．50° C．60° D．75° 8．（3分）如图，在平面直角坐标系中，点A（﹣1，m）在直线y=2x+3上，连结OA，将线段OA绕点O顺时针旋转90°，点A的对应点B恰好落在直线y=﹣x+b 上，则b的值为（　　） A．﹣2 B．1 C． D．2 　二、填空题（本大题共6小题，每小题3分，共18分） 9．（3分）比较大小：　1．（填“＞”、“=”或“＜”） 10．（3分）不等式3x﹣12≥0的解集为　． 11．（3分）如图，PA为⊙O的切线，A为切点，B是OP与⊙O的交点．若∠P=20° 第2页（共35页），OA=3，则的长为　（结果保留π） 12．（3分）如图，在平面直角坐标系中，点P在函数y= （x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足分别为A、B，取线段OB的中点C，连结P C并延长交x轴于点D．则△APD的面积为　． 13．（3分）如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为　． 14．（3分）如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为　．第3页（共35页）　三、解答题（本大题共10小题，共78分） 15．（6分）先化简，再求值：（x+1）2+x（x﹣2），其中x= ．16．（6分）一个不透明的盒子中有三张卡片，卡片上面分别标有字母a，b，c ，每张卡片除字母不同外其他都相同，小玲先从盒子中随机抽出一张卡片，记下字母后放回并搅匀；再从盒子中随机抽出一张卡片并记下字母，用画树状图（或列表）的方法，求小玲两次抽出的卡片上的字母相同的概率． 17．（6分）为了美化环境，某地政府计划对辖区内60km2的土地进行绿化．为了尽快完成任务．实际平均每月的绿化面积是原计划的1.5倍．结果提前2个月完成任务，求原计划平均每月的绿化面积．第4页（共35页） 18．（7分）如图，CE是△ABC外角∠ACD的平分线，AF∥CD交CE于点F，FG∥A C交CD于点G．求证：四边形ACGF是菱形． 19．（7分）如图，海面上B、C两岛分别位于A岛的正东和正北方向．一艘船从 A岛出发，以18海里/时的速度向正北方向航行2小时到达C岛，此时测得B岛在C岛的南偏东43°．求A、B两岛之间的距离．（结果精确到0.1海里）【参考数据：sin43°=0.68，cos43°=0.73，tan43°=0.93】 20．（7分）在“世界家庭日”前夕，某校团委随机抽取了n名本校学生，对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查．问卷中的家庭活动方式包括：第5页（共35页） A．在家里聚餐； B．去影院看电影； C．到公园游玩； D．进行其他活动每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式，该校团委收回全部问卷后，将收集到的数据整理并绘制成如图所示的统计图，根据统计图提供的信息，解答下列问题：（1）求n的值；（2）四种方式中最受学生喜欢的方式为　（用A、B、C、D作答）；选择该种方式的学生人数占被调查的学生人数的百分比为　．（3）根据统计结果，估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数． 21．（8分）甲、乙两台机器共同加工一批零件，在加工过程中两台机器均改变了一次工作效率．从工作开始到加工完这批零件两台机器恰好同时工作6小时．甲、乙两台机器各自加工的零件个数y（个）与加工时间x（时）之间的函数图象分别为折线OA﹣AB与折线OC﹣CD．如图所示．（1）求甲机器改变工作效率前每小时加工零件的个数．（2）求乙机器改变工作效率后y与x之间的函数关系式．第6页（共35页）（3）求这批零件的总个数． 22．（9分）在矩形ABCD中，已知AD＞AB．在边AD上取点E，使AE=AB，连结CE ，过点E作EF⊥CE，与边AB或其延长线交于点F．猜想：如图①，当点F在边AB上时，线段AF与DE的大小关系为　．探究：如图②，当点F在边AB的延长线上时，EF与边BC交于点G．判断线段AF与 DE的大小关系，并加以证明．应用：如图②，若AB=2，AD=5，利用探究得到的结论，求线段BG的长． 23．（10分）如图，在等边△ABC中，AB=6，AD⊥BC于点D．点P在边AB上运动，过点P作PE∥BC，与边AC交于点E，连结ED，以PE、ED为邻边作▱PEDF．设 ▱PEDF与△ABC重叠部分图形的面积为y，线段AP的长为x（0＜x＜6）．第7页（共35页）（1）求线段PE的长．（用含x的代数式表示）（2）当四边形PEDF为菱形时，求x的值．（3）求y与x之间的函数关系式．（4）设点A关于直线PE的对称点为点A′，当线段A′B的垂直平分线与直线AD相交时，设其交点为Q，当点P与点Q位于直线BC同侧（不包括点Q在直线BC上）时，直接写出x的取值范围． 24．（12分）如图，在平面直角坐标系中，抛物线y=a（x﹣1）2+4与x轴交于点第8页（共35页） A、B两点，与y轴交于点C，且点B的坐标为（3，0），点P在这条抛物线上，且不与B、C两点重合．过点P作y轴的垂线与射线BC交于点Q，以PQ为边作Rt △PQF，使∠PQF=90°，点F在点Q的下方，且QF=1．设线段PQ的长度为d，点 P的横坐标为m．（1）求这条抛物线所对应的函数表达式．（2）求d与m之间的函数关系式．（3）当Rt△PQF的边PF被y轴平分时，求d的值．（4）以OB为边作等腰直角三角形OBD，当0＜m＜3时，直接写出点F落在△OB D的边上时m的值．　第9页（共35页） 2015年吉林省长春市中考数学试卷参考答案与试题解析　一、选择题（本大题共8小题，每小题3分，共24分） 1．（3分）﹣3的绝对值是（　　） A．3 B．﹣3 C． D．【考点】15：绝对值．菁优网版权所有【分析】根据一个负数的绝对值等于它的相反数得出．【解答】解：|﹣3|=﹣（﹣3）=3．故选：A．【点评】考查绝对值的概念和求法．绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0． 2．（3分）在长春市“暖房子工程”实施过程中，某工程队做了面积为632000m2 的外墙保暖．632000这个数用科学记数法表示为（　　） A．63.2×104 B．6.32×105 C．0.632×106 D．0.632×106 【考点】1I：科学记数法—表示较大的数．菁优网版权所有【分析】用科学记数法表示，科学记数法的表示形式为a×10n的形式，其中1≤ |a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：632000=6.32×105，故选：B．第10页（共35页）【点评】此题主要考查了科学记数法的表示方法．科学记数法的表示形式为a× 10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n 的值． 3．（3分）计算（a2）3的结果是（　　） A．3a2 B．a5 C．a6 D．a3 【考点】47：幂的乘方与积的乘方．菁优网版权所有【分析】根据幂的乘方计算即可．【解答】解：（a2）3=a6，故选：C．【点评】此题考查幂的乘方，关键是根据法则进行计算． 4．（3分）图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（　　） A．主视图相同 B．俯视图相同 C．左视图相同 D．主视图、俯视图、左视图都相同【考点】U2：简单组合体的三视图．菁优网版权所有【分析】根据从正面看得到的视图是主视图，从左边看得到的图形是左视图，从上面看得到的图形是俯视图，可得答案．【解答】解：A、主视图的宽不同，故A错误；第11页（共35页） B、俯视图是两个相等的圆，故B正确； C、主视图的宽不同，故C错误； D、俯视图是两个相等的圆，故D错误；故选：B．【点评】本题考查了简单组合体的三视图，从正面看得到的视图是主视图，从左边看得到的图形是左视图，从上面看得到的图形是俯视图． 5．（3分）方程x2﹣2x+3=0的根的情况是（　　） A．有两个相等的实数根 C．没有实数根 B．只有一个实数根 D．有两个不相等的实数根【考点】AA：根的判别式．菁优网版权所有【分析】把a=1，b=﹣2，c=3代入△=b2﹣4ac进行计算，然后根据计算结果判断方程根的情况．【解答】解：∵a=1，b=﹣2，c=3， ∴△=b2﹣4ac=（﹣2）2﹣4×1×3=﹣8＜0，所以方程没有实数根．故选：C．【点评】本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2﹣4ac．当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程没有实数根． 6．（3分）如图，在△ABC中，AB=AC，过点A作AD∥BC．若∠1=70°，则∠BAC 的大小为（　　）第12页（共35页） A．30° B．40° C．50° D．70° 【考点】JA：平行线的性质．菁优网版权所有【分析】根据平行线的性质求出∠C，根据等腰三角形的性质得出∠B=∠C=70° ，根据三角形内角和定理求出即可．【解答】解：∵AB=AC， ∴∠B=∠C， ∵AD∥BC，∠1=70°， ∴∠C=∠1=70°， ∴∠B=70°， ∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣70°=40°，故选：B．【点评】本题考查了三角形内角和定理，等腰三角形的性质，平行线的性质的应用，解此题的关键是求出∠C的度数和得出∠B=∠C，注意：三角形内角和等于180°，两直线平行，内错角相等． 7．（3分）如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ ADC的大小为（　　） A．45° B．50° C．60° D．75° 【考点】L5：平行四边形的性质；M5：圆周角定理；M6：圆内接四边形的性第13页（共35页）质．菁优网版权所有【分析】设∠ADC的度数=α，∠ABC的度数=β，由题意可得，求出β即可解决问题．【解答】解：设∠ADC的度数=α，∠ABC的度数=β； ∵四边形ABCO是平行四边形， ∴∠ABC=∠AOC； ∵∠ADC= β，∠ADC=α；而α+β=180°， ∴，解得：β=120°，α=60°，∠ADC=60°，故选：C．【点评】该题主要考查了圆周角定理及其应用问题；应牢固掌握该定理并能灵活运用． 8．（3分）如图，在平面直角坐标系中，点A（﹣1，m）在直线y=2x+3上，连结OA，将线段OA绕点O顺时针旋转90°，点A的对应点B恰好落在直线y=﹣x+b 上，则b的值为（　　） A．﹣2 B．1 C． D．2 【考点】F8：一次函数图象上点的坐标特征；R7：坐标与图形变化﹣旋转．菁优网版权所有【专题】16：压轴题．第14页（共35页）【分析】先把点A坐标代入直线y=2x+3，得出m的值，然后得出点B的坐标，再代入直线y=﹣x+b解答即可．【解答】解：把A（﹣1，m）代入直线y=2x+3，可得：m=﹣2+3=1，因为线段OA绕点O顺时针旋转90°，所以点B的坐标为（1，1），把点B代入直线y=﹣x+b，可得：1=﹣1+b，b=2，故选：D．【点评】此题考查一次函数问题，关键是根据代入法解解析式进行分析．　二、填空题（本大题共6小题，每小题3分，共18分） 9．（3分）比较大小：＞　1．（填“＞”、“=”或“＜”）【考点】2A：实数大小比较．菁优网版权所有【分析】根据实数大小比较的方法，判断出两个数的平方的大小故选，即可判断出两个数的大小关系．【解答】解：，∵2＞1， ∴．故答案为：＞．【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是判断出两个数的平方的大小关系． 10．（3分）不等式3x﹣12≥0的解集为　x≥4　．【考点】C6：解一元一次不等式．菁优网版权所有【分析】利用不等式的基本性质，把12移到不等号的右边，系数化为1即可求得原不等式的解集．【解答】解：移项得，3x≥12，第15页（共35页）解得x≥4，故答案为x≥4．【点评】本题考查了解一元一次不等式，以及解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．解不等式要依据不等式的基本性质：（1）不等式的两边同时加上或减去同一个数或整式不等号的方向不变；（2）不等式的两边同时乘以或除以同一个正数不等号的方向不变；（3）不等式的两边同时乘以或除以同一个负数不等号的方向改变． 11．（3分）如图，PA为⊙O的切线，A为切点，B是OP与⊙O的交点．若∠P=20° ，OA=3，则的长为　 π　（结果保留π）【考点】MC：切线的性质；MN：弧长的计算．菁优网版权所有【分析】根据切线性质得出∠OAP=90°，求出∠POA度数，根据弧长公式求出即可．【解答】解：∵PA切⊙O于A， ∴∠PAO=90°， ∵∠P=20°， ∴∠POA=70°， ∴= π，故答案为： π．【点评】本题考查了弧长公式，切线的性质的应用，能正确运用弧长公式进行计算是解此题的关键，注意：圆的切线垂直于过切点的半径．第16页（共35页） 12．（3分）如图，在平面直角坐标系中，点P在函数y= （x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足分别为A、B，取线段OB的中点C，连结P C并延长交x轴于点D．则△APD的面积为　6　．【考点】G5：反比例函数系数k的几何意义；KD：全等三角形的判定与性质．菁优网版权所有【分析】根据已知条件证得△PBC≌△DOC，再根据反比例函数系数k的几何意义即可得到结论．【解答】解：∵PB⊥y轴，PA⊥x轴， ∴S矩形APBO=|k|=6，在△PBC与△DOC中，，∴△PBC≌△DOC， ∴S△APD=S矩形APBO=6．故答案为：6．【点评】本题考查了反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|，全等三角形的判定和性质，证明△PBC≌△DOC是解题的关键． 13．（3分）如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为　5　．第17页（共35页）【考点】K3：三角形的面积；KQ：勾股定理；LE：正方形的性质．菁优网版权所有【分析】根据正方形性质得出AD=BC=CD=AB，根据面积求出EM，得出BC=4，根据勾股定理求出即可．【解答】解：过E作EM⊥AB于M， ∵四边形ABCD是正方形， ∴AD=BC=CD=AB， ∴EM=AD，BM=CE， ∵△ABE的面积为8， ∴ ×AB×EM=8，解得：EM=4，即AD=DC=BC=AB=4， ∵CE=3，由勾股定理得：BE= 故答案为：5． ==5，【点评】本题考查了三角形面积，正方形性质，勾股定理的应用，解此题的关键是求出BC的长，难度适中． 14．（3分）如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的第18页（共35页）最小值为　1　．【考点】H5：二次函数图象上点的坐标特征；J4：垂线段最短；LB：矩形的性质．菁优网版权所有【专题】11：计算题；16：压轴题．【分析】先利用配方法得到抛物线的顶点坐标为（1，1），再根据矩形的性质得BD=AC，由于AC的长等于点A的纵坐标，所以当点A在抛物线的顶点时，点 A到x轴的距离最小，最小值为1，从而得到BD的最小值．【解答】解：∵y=x2﹣2x+2=（x﹣1）2+1， ∴抛物线的顶点坐标为（1，1）， ∵四边形ABCD为矩形， ∴BD=AC，而AC⊥x轴， ∴AC的长等于点A的纵坐标，当点A在抛物线的顶点时，点A到x轴的距离最小，最小值为1， ∴对角线BD的最小值为1．故答案为1．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了矩形的性质．　三、解答题（本大题共10小题，共78分）第19页（共35页） 15．（6分）先化简，再求值：（x+1）2+x（x﹣2），其中x= 【考点】4J：整式的混合运算—化简求值．菁优网版权所有【专题】11：计算题．．【分析】原式第一项利用完全平方公式化简，第二项利用单项式乘以多项式法则计算，去括号合并得到最简结果，把x的值代入计算即可求出值．【解答】解：原式=x2+2x+1+x2﹣2x=2×2+1，当x= 时，原式=6+1=7．【点评】此题考查了整式的混合运算﹣化简求值，熟练掌握运算法则是解本题的关键． 16．（6分）一个不透明的盒子中有三张卡片，卡片上面分别标有字母a，b，c ，每张卡片除字母不同外其他都相同，小玲先从盒子中随机抽出一张卡片，记下字母后放回并搅匀；再从盒子中随机抽出一张卡片并记下字母，用画树状图（或列表）的方法，求小玲两次抽出的卡片上的字母相同的概率．【考点】X6：列表法与树状图法．菁优网版权所有【专题】11：计算题．【分析】先画树状图展示所有9种等可能的结果数，再找出两次抽出的卡片上的字母相同的结果数，然后根据概率公式求解．【解答】解：画树状图为：共有9种等可能的结果数，其中两次抽出的卡片上的字母相同的结果数为3种，所有小玲两次抽出的卡片上的字母相同的概率= = ．【点评】本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可第20页（共35页）能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率． 17．（6分）为了美化环境，某地政府计划对辖区内60km2的土地进行绿化．为了尽快完成任务．实际平均每月的绿化面积是原计划的1.5倍．结果提前2个月完成任务，求原计划平均每月的绿化面积．【考点】B7：分式方程的应用．菁优网版权所有【分析】设原计划平均每月的绿化面积为xkm2，实际平均每月的绿化面积是1.5 xkm2，根据结果提前2个月完成任务列出方程解答即可．【解答】解：设原计划平均每月的绿化面积为xkm2，实际平均每月的绿化面积是1.5xkm2，由题意得 ﹣=2 解得：x=10 经检验x=10是原方程的解，答：原计划平均每月的绿化面积为10km2．【点评】此题考查分是方程的实际运用，找到原计划所用时间和实际所用时间的等量关系是解决问题的关键． 18．（7分）如图，CE是△ABC外角∠ACD的平分线，AF∥CD交CE于点F，FG∥A C交CD于点G．求证：四边形ACGF是菱形．【考点】L9：菱形的判定．菁优网版权所有第21页（共35页）【专题】14：证明题．【分析】首先根据平行线的性质得到∠2=∠3，从而根据角平分线的性质得到∠ 1=∠3，得到AF=AC，从而利用邻边相等的平行四边形是菱形证得结论．【解答】证明：∵AF∥CD，FG∥AC， ∴四边形ACGF是平行四边形，∠2=∠3， ∵CE平分∠ACD， ∴∠1=∠2， ∴∠1=∠3， ∴AC=AF， ∴四边形ACGF是菱形．【点评】本题考查了菱形的判定，解题的关键是了解菱形的几种判定方法，难度不大． 19．（7分）如图，海面上B、C两岛分别位于A岛的正东和正北方向．一艘船从 A岛出发，以18海里/时的速度向正北方向航行2小时到达C岛，此时测得B岛在C岛的南偏东43°．求A、B两岛之间的距离．（结果精确到0.1海里）【参考数据：sin43°=0.68，cos43°=0.73，tan43°=0.93】【考点】TB：解直角三角形的应用﹣方向角问题．菁优网版权所有第22页（共35页）【分析】根据路程=速度×时间，可得AC=18×2=36海里，在Rt△ABC中，利用正切函数的定义可得AB=AC•tan∠ACB，将数值代入计算即可求解．【解答】解：由题意得，AC=18×2=36海里，∠ACB=43°．在Rt△ABC中，∵∠A=90°， ∴AB=AC•tan∠ACB=36×0.93≈33.5海里．故A、B两岛之间的距离约为33.5海里．【点评】本题考查了解直角三角形的应用﹣方向角问题，正切函数的定义，路程、速度与时间自己的关系，难度一般．理解方向角的定义，将实际问题转化为数学问题是解决问题的关键． 20．（7分）在“世界家庭日”前夕，某校团委随机抽取了n名本校学生，对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查．问卷中的家庭活动方式包括： A．在家里聚餐； B．去影院看电影； C．到公园游玩； D．进行其他活动每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式，该校团委收回全部问卷后，将收集到的数据整理并绘制成如图所示的统计图，根据统计图提供的信息，解答下列问题：（1）求n的值；（2）四种方式中最受学生喜欢的方式为　C　（用A、B、C、D作答）；选择该种方式的学生人数占被调查的学生人数的百分比为　35%　．（3）根据统计结果，估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数．第23页（共35页）【考点】V5：用样本估计总体；VC：条形统计图．菁优网版权所有【分析】（1）根据条形图，把A，B，C，D的人数加起来，即可解答；（2）C的学生人数最多，即为四种方式中最受学生喜欢的方式；用C的人数÷总人数，即可得到百分比；（3）分别计算出喜欢C方式的学生人数、喜欢B方式的学生的人数，作差即可解答．【解答】解：（1）n=30+40+70+60=200．（2）∵C的学生人数最多， ∴四种方式中最受学生喜欢的方式为C， ×100%=35%，故答案为：C，35%．（3）1800× =270（人），答：该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数为270人．【点评】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据． 21．（8分）甲、乙两台机器共同加工一批零件，在加工过程中两台机器均改变第24页（共35页）了一次工作效率．从工作开始到加工完这批零件两台机器恰好同时工作6小时．甲、乙两台机器各自加工的零件个数y（个）与加工时间x（时）之间的函数图象分别为折线OA﹣AB与折线OC﹣CD．如图所示．（1）求甲机器改变工作效率前每小时加工零件的个数．（2）求乙机器改变工作效率后y与x之间的函数关系式．（3）求这批零件的总个数．【考点】FH：一次函数的应用．菁优网版权所有【分析】（1）甲改变工作效率前的工作效率为改变前加工的总件数，除以加工的总时间即可；（2）利用待定系数法求一次函数解析式即可；（3）利用函数解析式求出甲、乙两机器6小时加工的总件数，求其和即可．【解答】解：（1）80÷4=20（件）；（2）设AB与CD的交点为P，由图可以P坐标为（5，110） ∵图象过C（2，80），P（5，110）， ∴设解析式为y=kx+b（k≠0）， ∴，解得：，∴y乙=10x+60（2≤x≤6）；（3）∵AB过（4，80），P（5，110），第25页（共35页） ∴设AB的解析式为y甲=mx+n（m≠0），，解得： ∴y甲=30x﹣40（4≤x≤6）， ∴，当x=6时，y甲=30×6﹣40=140，y乙=10×6+60=120， ∴这批零件的总个数是140+120=260．【点评】此题主要考查了一次函数的应用，根据题意得出函数关系式以及数形结合是解决问题的关键． 22．（9分）在矩形ABCD中，已知AD＞AB．在边AD上取点E，使AE=AB，连结CE ，过点E作EF⊥CE，与边AB或其延长线交于点F．猜想：如图①，当点F在边AB上时，线段AF与DE的大小关系为　AF=DE　．探究：如图②，当点F在边AB的延长线上时，EF与边BC交于点G．判断线段AF与 DE的大小关系，并加以证明．应用：如图②，若AB=2，AD=5，利用探究得到的结论，求线段BG的长．【考点】LO：四边形综合题．菁优网版权所有【分析】①根据题意证明△AEF≌△DCE即可； ②证明方法与①相同可以证明结论； ③根据平行线分线段成比例定理列出比例式，计算得到答案．【解答】解：①AF=DE； ②AF=DE，第26页（共35页）证明：∵∠A=∠FEC=∠D=90°， ∴∠AEF=∠DCE，在△AEF和△DCE中，，∴△AEF≌△DCE， ∴AF=DE． ③∵△AEF≌△DCE， ∴AE=CD=AB=2，AF=DE=3，FB=FA﹣AB=1， ∵BG∥AD， ∴=，∴BG= ．【点评】本题考查的是矩形的性质、全等三角形的判定和性质、相似三角形的性质和判定，灵活运用相关的定理和性质是解题的关键． 23．（10分）如图，在等边△ABC中，AB=6，AD⊥BC于点D．点P在边AB上运动，过点P作PE∥BC，与边AC交于点E，连结ED，以PE、ED为邻边作▱PEDF．设 ▱PEDF与△ABC重叠部分图形的面积为y，线段AP的长为x（0＜x＜6）．（1）求线段PE的长．（用含x的代数式表示）（2）当四边形PEDF为菱形时，求x的值．（3）求y与x之间的函数关系式．（4）设点A关于直线PE的对称点为点A′，当线段A′B的垂直平分线与直线AD相交时，设其交点为Q，当点P与点Q位于直线BC同侧（不包括点Q在直线BC上）时，直接写出x的取值范围．第27页（共35页）【考点】LO：四边形综合题．菁优网版权所有【专题】16：压轴题．【分析】（1）证明△APE是等边三角形，即可求解；（2）四边形PEDF为菱形时，AE=DE，然后证明DE=EC即可得到E是AC的中点，则 P是AB的中点，据此即可求解；（3）当x=3，即P是AB的中点时，PE= BC，则F与B重合，当0＜x≤3时，重合部分就是平行四边形PEDF，当3＜x≤6时，重合部分是梯形PEDB，根据平行四边形和梯形的面积公式即可求解；（4）首先求得当A’B的中垂线正好经过点D时x的值，据此即可求解．【解答】解：（1）∵PE∥BC， ∴△APE∽△ABC，又∵△ABC是等边△， ∴△APE是等边三角形， ∴PE=AP=x（0＜x＜6）；（2）∵四边形PEDF为菱形， ∴PE=DE=x，又∵△APE是等边三角形，则AE=PE， ∴AE=DE， ∴∠DAC=∠ADE，第28页（共35页）又∵∠ADE+∠EDC=∠DAC+∠C=90°， ∴∠EDC=∠C， ∴DE=EC， ∴DE=EC=AE= AC= AB=3．即x=3；（3）当x=3，即P是AB的中点时，PE= BC，则F与B重合．则当0＜x≤3时，重合部分就是平行四边形PEDF，如图1．等边△ABC中，AD=AB•sin60°=6× =3 ，等边△APE中，AM=AP•sin60°= x，则DM=3 ﹣x， x），即y=﹣ x2+3 x；则y=x（3 ﹣当3＜x＜6时，重合部分是梯形PEDB，如图2．则y= （PE+BD）•DM= （x+3）•（3 ﹣x），即y=﹣ ；（4）情形一：当A′在BC上方时，如图3所示，当A′B的中垂线正好经过点D时，A′D=BD=3，则AA′=3 ﹣3．则AM= AA′= （3 ﹣3）， ∴x=AP= =3﹣ ．则x的取值范围是：0＜x＜3﹣ ．情形二：当A′在BC上时，PQ∥AD，如图4所示，第29页（共35页） AP=A′P=BP= AB= ×6=3．情形三：当A′在BC下方时，如图5所示，当A′B的中垂线正好经过点D时，A′D=BD=3，则AA′=3 +3．则AM= AA′= （3 +3）， ∴x=AP= =3+ ．则x的取值范围是：3＜x＜3+ ．综上所示，x的取值范围为0＜x＜3﹣ 或3＜x＜3+ ．第30页（共35页）【点评】本题是等边三角形的性质以及菱形的性质的综合应用，求得F与B重合以及A’B的中垂线正好经过点D时，两种情况下t的值是关键． 24．（12分）如图，在平面直角坐标系中，抛物线y=a（x﹣1）2+4与x轴交于点 A、B两点，与y轴交于点C，且点B的坐标为（3，0），点P在这条抛物线上，且不与B、C两点重合．过点P作y轴的垂线与射线BC交于点Q，以PQ为边作Rt △PQF，使∠PQF=90°，点F在点Q的下方，且QF=1．设线段PQ的长度为d，点 P的横坐标为m．（1）求这条抛物线所对应的函数表达式．（2）求d与m之间的函数关系式．（3）当Rt△PQF的边PF被y轴平分时，求d的值．（4）以OB为边作等腰直角三角形OBD，当0＜m＜3时，直接写出点F落在△OB D的边上时m的值．【考点】HF：二次函数综合题．菁优网版权所有【专题】16：压轴题．【分析】（1）把点B（3，0）代入抛物线y=a（x﹣1）2+4，求出a的值即可；（2）先求出直线BC的解析式，由点Q的纵坐标求出横坐标，求出PQ，即可得出结果；（3）由题意得出点P与点Q关于y轴对称，得出方程，解方程即可；第31页（共35页）（4）分两种情况：①当点F落在△OBD的直角边上时，延长QF交OB于G，证出 △OFG是等腰直角三角形，得出OG=FG，由FG=QG﹣QF，得出方程，解方程即可； ②当点F落在△OBD的斜边上时，证出△BQF是等腰直角三角形，得出BF=QF=1， OF=2，得出方程，解方程即可．【解答】解：（1）把点B（3，0）代入抛物线y=a（x﹣1）2+4，得：4a+4=0，解得：a=﹣1， ∴抛物线的函数表达式为：y=﹣（x﹣1）2+4=﹣x2+2x+3，即抛物线解析式为：y=﹣x2+2x+3；（2）对于抛物线y=﹣x2+2x+3，当x=0时，y=3；当y=0时，x=﹣1，或x=3， ∴C（0，3），A（﹣1，0），B（3，0），设直线BC的解析式为：y=kx+b，根据题意得：，解得：k=﹣1，b=3， ∴直线BC的解析式为：y=﹣x+3， ∵点P的坐标为：（m，﹣m2+2m+3）， ∴点Q的纵坐标坐标为：﹣m2+2m+3，则﹣x+3=﹣m2+2m+3，x=m2﹣2m， ∴点Q的坐标为（m2﹣2m，﹣m2+2m+3）， ∴当﹣1≤m＜0时，如图1，第32页（共35页） d=m2﹣2m﹣m=m2﹣3m，当0＜m＜3时，如图2， d=m﹣（m2﹣2m）=﹣m2+3m ∴d与m之间的函数关系式为：d= ；（3）当Rt△PQF的边PF被y轴平分时，点P与点Q关于y轴对称， ∴横坐标互为相反数， ∴m2﹣2m+m=0，解得：m=1，或m=0（不合题意，舍去）， ∴m=1， ∴d=3﹣1=2；（4）分四种情况： ①情形一：如图4所示， ∵C点的坐标为（0，3），将y=3代入函数y=﹣x2+2x+3得x1=0（舍去），x2=2，第33页（共35页） ∴P点的横坐标m=2； ②情形二：如图5所示：过D2点作D2G⊥CO交QF与N点， ∵B（3，0） ∴D2（，）， ∵CO=3，QF=1，QF∥CO， ∴=，∴D2N= ， ∴Q（1，2），将y=2代入函数y=﹣x2+2x+3得x1=1+ ，x2=1﹣ （舍去）， ∴m=1+ ；③情形三：如图6所示：过D2点作D2G⊥OB， ∵B（3，0） ∴D2（，）， ∵BG= ，QF=1，QF∥CO， ∴，∴BF=1， ∴Q（1，1），将y=1代入函数y=﹣x2+2x+3得x1=1+ ，x2=1﹣ （舍去）， ∴m=1+ ；④情形四：如图7所示： ∵CD4=6，QF=1，BC=3 ，且QF∥CD2， ∴，∴BQ= ，∴Q点纵坐标为，即P点纵坐标，第34页（共35页）将y= 代入函数y=﹣x2+2x+3得x1= ∴m= 综上所述：当0＜m＜3时，点F落在△OBD的边上时m的值为：2，或1+ ，或1 ，或，x2= （舍去），．+．【点评】本题是二次函数综合题目，考查了二次函数解析式的求法、轴对称的性质、用待定系数法求一次函数解析式、等腰直角三角形的判定与性质、一元二次方程的解法等知识；本题难度较大，综合性强，特别是（4）中，需要进行分类讨论，画出图形，证明等腰直角三角形和解一元二次方程才能得出结果．　第35页（共35页）