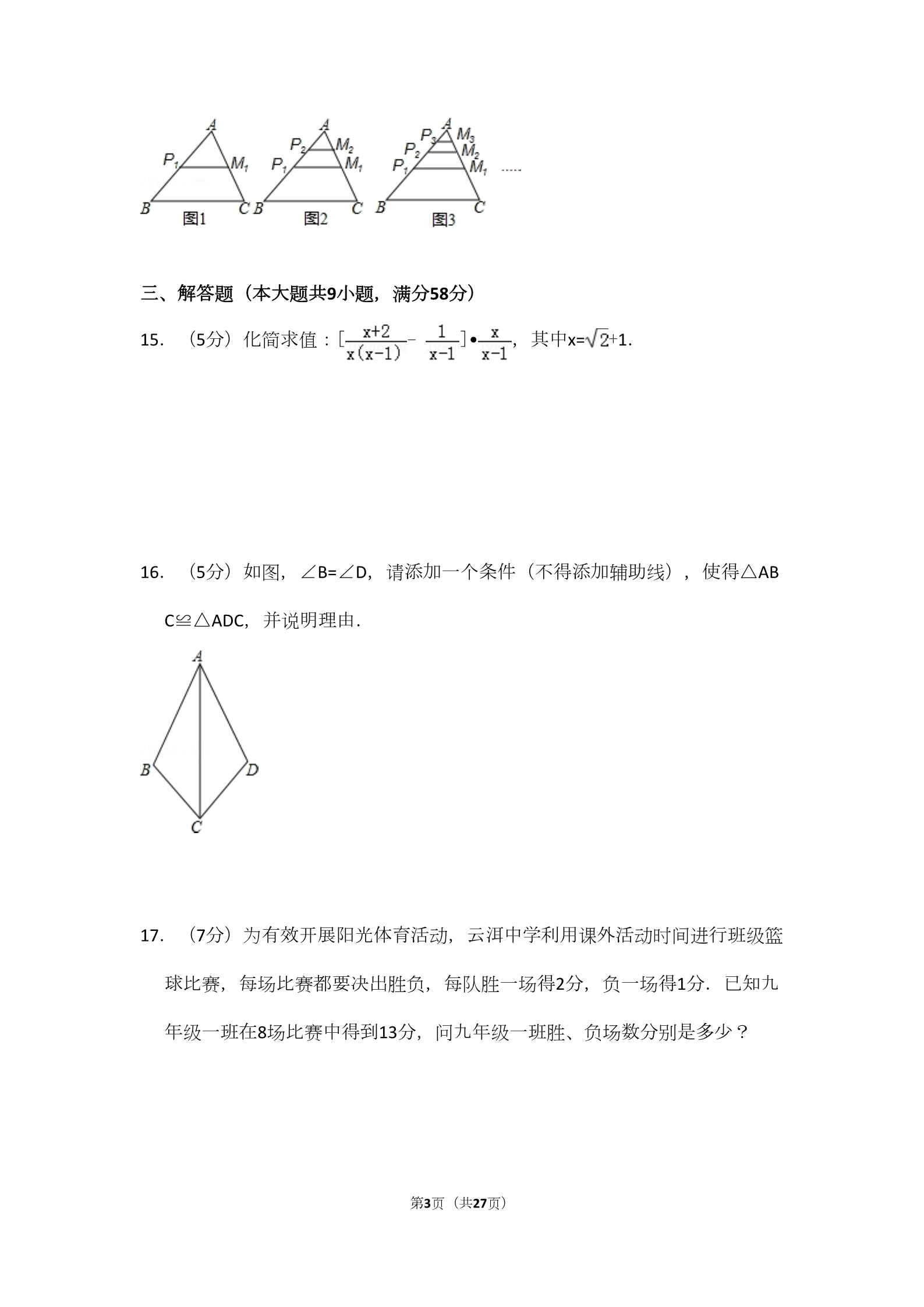
2015年云南省中考数学试卷（省卷）（含解析版）

2015年云南省中考数学试卷一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，满分24 分） 1．（3分）﹣2的相反数是（　　） A．﹣2 2．（3分）不等式2x﹣6＞0的解集是（　　） A．x＞1 B．x＜﹣3 C．x＞3 B．2 C．﹣ D． D．x＜3 3．（3分）若一个几何体的主视图、左视图、俯视图都是正方形，则这个几何体是（　　） A．正方体 B．圆锥 C．圆柱 D．球 4．（3分）2011年国家启动实施农村义务教育学生营养改善计划，截至2014年4 月，我省开展营养改善试点中小学达17580所，17580这个数用科学记数法可表示为（　　） A．17.58×103 B．175.8×104 C．1.758×105 D．1.758×104 5．（3分）下列运算正确的是（　　） A．a2•a5=a10 B．（π﹣3.14）0=0 D．（a+b）2=a2+b2 C． ﹣2 =6．（3分）下列一元二次方程中，没有实数根的是（　　） A．4×2﹣5x+2=0 B．x2﹣6x+9=0 C．5×2﹣4x﹣1=0 D．3×2﹣4x+1=0 7．（3分）为加快新农村试点示范建设，我省开展了“美丽乡村”的评选活动，下表是我省六个州（市）推荐候选的“美丽乡村”个数统计结果： ABCDEF州（市） 36 27 31 56 48 54 推荐数（个）第1页（共27页）在上表统计的数据中，平均数和中位数分别为（　　） A．42，43.5 B．42，42 C．31，42 D．36，54 8．（3分）若扇形面积为3π，圆心角为60°，则该扇形的半径为（　　） A．3 B．9 C．2 D．3 　二、填空题（本大题共6小题，每小题3分，满分18分） 9．（3分）分解因式：3×2﹣12=　． 10．（3分）函数y= 的自变量x的取值范围是　． 11．（3分）如图，直线l1∥l2，并且被直线l3，l4所截，则∠α=　． 12．（3分）一台电视机原价是2500元，现按原价的8折出售，则购买a台这样的电视机需要　元． 13．（3分）如图，点A，B，C是⊙O上的点，OA=AB，则∠C的度数为　． 14．（3分）如图，在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2 ，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，按这样的规律下去，PnMn的长为　（n为正整数）．第2页（共27页）　三、解答题（本大题共9小题，满分58分） 15．（5分）化简求值：[ ﹣]• ，其中x= +1． 16．（5分）如图，∠B=∠D，请添加一个条件（不得添加辅助线），使得△AB C≌△ADC，并说明理由． 17．（7分）为有效开展阳光体育活动，云洱中学利用课外活动时间进行班级篮球比赛，每场比赛都要决出胜负，每队胜一场得2分，负一场得1分．已知九年级一班在8场比赛中得到13分，问九年级一班胜、负场数分别是多少？第3页（共27页） 18．（5分）已知A，B两地相距200千米，一辆汽车以每小时60千米的速度从A 地匀速驶往B地，到达B地后不再行驶，设汽车行驶的时间为x小时，汽车与B 地的距离为y千米．（1）求y与x的函数关系，并写出自变量x的取值范围；（2）当汽车行驶了2小时时，求汽车距B地有多少千米？ 19．（6分）为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据： ≈1.41， ≈1.73，结果保留整数）第4页（共27页） 20．（7分）现有一个六面分别标有数字1，2，3，4，5，6且质地均匀的正方形骰子，另有三张正面分别标有数字1，2，3的卡片（卡片除数字外，其他都相同），先由小明投骰子一次，记下骰子向上一面出现的数字，然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张，记下卡片上的数字．（1）请用列表或画树形图（树状图）的方法，求出骰子向上一面出现的数字与卡片上的数字之积为6的概率；（2）小明和小王做游戏，约定游戏规则如下：若骰子向上一面出现的数字与卡片上的数字之积大于7，则小明赢；若骰子向上一面出现的数字与卡片上的数字之积小于7，则小王赢，问小明和小王谁赢的可能性更大？请说明理由．21．（7分）2015年某省为加快建设综合交通体系，对铁路、公路、机场三个重大项目加大了建设资金的投入．第5页（共27页）（1）机场建设项目中所有6个机场投入的建设资金金额统计如图1，已知机场E 投入的建设资金金额是机场C，D所投入建设资金金额之和的三分之二，求机场E投入的建设资金金额是多少亿元？并补全条形统计图；（2）将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表，根据扇形统计图及统计表中信息，求得a=　，b=　，c　，d　，m　．（请直接填写计算结果）铁路公路机场铁路、公路、机场三项投入建设资金总金额（亿元） 300 abm投入资金（亿元）c34% d6% 所占百分比所占圆心角 216° 21.6° 第6页（共27页） 22．（7分）如图，在矩形ABCD中，AB=4，AD=6，M，N分别是AB，CD的中点，P是AD上的点，且∠PNB=3∠CBN．（1）求证：∠PNM=2∠CBN；（2）求线段AP的长． 23．（9分）如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A （1，0），C（0，3），且BC=5．（1）分别求直线BC和抛物线的解析式（关系式）；（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．　第7页（共27页） 2015年云南省中考数学试卷参考答案与试题解析　一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，满分24 分） 1．（3分）﹣2的相反数是（　　） A．﹣2 B．2 C．﹣ D．【考点】14：相反数．菁优网版权所有【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可．【解答】解：﹣2的相反数是：﹣（﹣2）=2，故选：B．【点评】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣ ”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0 ．不要把相反数的意义与倒数的意义混淆． 2．（3分）不等式2x﹣6＞0的解集是（　　） A．x＞1 B．x＜﹣3 C．x＞3 D．x＜3 【考点】C6：解一元一次不等式．菁优网版权所有【分析】利用不等式的基本性质：移项，系数化1来解答．【解答】解：移项得，2x＞6，两边同时除以2得，x＞3．故选：C．【点评】本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．第8页（共27页）解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变． 3．（3分）若一个几何体的主视图、左视图、俯视图都是正方形，则这个几何体是（　　） A．正方体 B．圆锥 C．圆柱 D．球【考点】U3：由三视图判断几何体．菁优网版权所有【分析】找到从正面、左面和上面看得到的图形是正方形的几何体即可．【解答】解：∵主视图和左视图都是正方形， ∴此几何体为柱体， ∵俯视图是一个正方形， ∴此几何体为正方体．故选：A．【点评】此题考查三视图，关键是根据：三视图里有两个相同可确定该几何体是柱体，锥体还是球体，由另一个视图确定其具体形状． 4．（3分）2011年国家启动实施农村义务教育学生营养改善计划，截至2014年4 月，我省开展营养改善试点中小学达17580所，17580这个数用科学记数法可表示为（　　） A．17.58×103 B．175.8×104 C．1.758×105 D．1.758×104 【考点】1I：科学记数法—表示较大的数．菁优网版权所有【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小第9页（共27页）数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1 时，n是负数．【解答】解：将17580用科学记数法表示为1.758×104．故选：D．【点评】本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．5．（3分）下列运算正确的是（　　） A．a2•a5=a10 C． ﹣2 B．（π﹣3.14）0=0 D．（a+b）2=a2+b2 =【考点】46：同底数幂的乘法；4C：完全平方公式；6E：零指数幂；78：二次根式的加减法．菁优网版权所有【分析】根据同底数幂的乘法、零指数幂、二次根式的加减和完全平方公式计算判断即可．【解答】解：A、a2•a5=a7，错误； B、（π﹣3.14）0=1，错误； C、，正确； D、（a+b）2=a2+2ab+b2，错误；故选：C．【点评】此题考查同底数幂的乘法、零指数幂、二次根式的加减和完全平方公式，关键是根据法则进行计算． 6．（3分）下列一元二次方程中，没有实数根的是（　　） A．4×2﹣5x+2=0 B．x2﹣6x+9=0 C．5×2﹣4x﹣1=0 D．3×2﹣4x+1=0 第10页（共27页）【考点】AA：根的判别式．菁优网版权所有【分析】分别计算出每个方程的判别式即可判断．【解答】解：A、∵△=25﹣4×2×4=﹣7＜0，∴方程没有实数根，故本选项正确； B、∵△=36﹣4×1×4=0，∴方程有两个相等的实数根，故本选项错误； C、∵△=16﹣4×5×（﹣1）=36＞0，∴方程有两个相等的实数根，故本选项错误； D、∵△=16﹣4×1×3=4＞0，∴方程有两个相等的实数根，故本选项错误；故选：A．【点评】本题考查了根的判别式，一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根． 7．（3分）为加快新农村试点示范建设，我省开展了“美丽乡村”的评选活动，下表是我省六个州（市）推荐候选的“美丽乡村”个数统计结果： ABCDEF州（市） 36 27 31 56 48 54 推荐数（个）在上表统计的数据中，平均数和中位数分别为（　　） A．42，43.5 B．42，42 C．31，42 D．36，54 【考点】W2：加权平均数；W4：中位数．菁优网版权所有【分析】根据平均数的公式求得上表统计的数据中的平均数，将其按从小到大的顺序排列中间的那个是中位数．【解答】解：P= （36+27+31+56+48+54）=42，第11页（共27页）把这几个数据按从小到大顺序排列为：27，31，36，48，54，56，中位数W= （36+48）=42．故选：B．【点评】本题考查了平均数和中位数的知识，属于基础题，解答本题的关键是熟练掌握平均数和中位数的定义． 8．（3分）若扇形面积为3π，圆心角为60°，则该扇形的半径为（　　） A．3 B．9 C．2 D．3 【考点】MO：扇形面积的计算．菁优网版权所有【分析】已知了扇形的圆心角和面积，可直接根据扇形的面积公式求半径长．【解答】解：扇形的面积= =3π．解得：r=3 故选：D．．【点评】本题主要考查了扇形的面积公式= ．熟练将公式变形是解题关键．　二、填空题（本大题共6小题，每小题3分，满分18分） 9．（3分）分解因式：3×2﹣12=　3（x﹣2）（x+2）　．【考点】55：提公因式法与公式法的综合运用．菁优网版权所有【分析】原式提取3，再利用平方差公式分解即可．【解答】解：原式=3（x2﹣4） =3（x+2）（x﹣2）．故答案为：3（x+2）（x﹣2）．【点评】本题考查因式分解．因式分解的步骤为：一提公因式；二看公式．公第12页（共27页）式包括平方差公式与完全平方公式，要能用公式法分解必须有平方项，如果是平方差就用平方差公式来分解，如果是平方和需要看还有没有两数乘积的 2倍，如果没有两数乘积的2倍还不能分解．解答这类题时一些学生往往因分解因式的步骤、方法掌握不熟练，对一些乘法公式的特点记不准确而误选其它选项．要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以提取公因式的要先提取公因式． 10．（3分）函数y= 的自变量x的取值范围是　x≥7　．【考点】E4：函数自变量的取值范围．菁优网版权所有【分析】函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数．【解答】解：根据题意得：x﹣7≥0，解得x≥7，故答案为x≥7．【点评】本题考查了函数自变量的取值范围问题，函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数． 11．（3分）如图，直线l1∥l2，并且被直线l3，l4所截，则∠α=　64°　．第13页（共27页）【考点】JA：平行线的性质．菁优网版权所有【分析】首先根据三角形外角的性质，求出∠1的度数是多少；然后根据直线l1 ∥l2，可得∠α=∠1，据此求出∠α的度数是多少即可．【解答】解：如图1， ∵∠1+56°=120°，，∴∠1=120°﹣56°=64°，又∵直线l1∥l2， ∴∠α=∠1=64°．故答案为：64°．【点评】此题主要考查了平行线的性质，要熟练掌握，解答此题的关键是要明确：（1）定理1：两条平行线被第三条直线所截，同位角相等．简单说成：两直线平行，同位角相等．（2）定理2：两条平行线被地三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．（3）定理3：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等． 12．（3分）一台电视机原价是2500元，现按原价的8折出售，则购买a台这样的电视机需要　2000a　元．【考点】32：列代数式．菁优网版权所有【分析】现在以8折出售，就是现价占原价的80%，把原价看作单位“1”，根据一个数乘百分数的意义，用乘法解答．第14页（共27页）【解答】解：2500a×80%=2000a（元）．故答案为2000a元．【点评】本题考查了列代数式，解题的关键是理解打折问题在实际问题中的应用． 13．（3分）如图，点A，B，C是⊙O上的点，OA=AB，则∠C的度数为　30°　．【考点】KM：等边三角形的判定与性质；M5：圆周角定理．菁优网版权所有【分析】由OA=AB，OA=OB，可得△OAB是等边三角形，即可得∠AOB=60°，又由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠C的度数．【解答】解：∵OA=AB，OA=OB， ∴OA=OB=AB，即△OAB是等边三角形， ∴∠AOB=60°， ∴∠C= ∠AOB=30°．故答案为30°．【点评】此题考查了圆周角定理与等边三角形的判定与性质．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用． 14．（3分）如图，在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2 ，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，按这样的第15页（共27页）规律下去，PnMn的长为　（n为正整数）．【考点】KX：三角形中位线定理．菁优网版权所有【专题】16：压轴题；2A：规律型．【分析】根据中位线的定理得出规律解答即可．【解答】解：在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2，M2 分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，可得：P1M1= ，P2M2= 故答案为：，故PnMn= ，【点评】此题考查三角形中位线定理，关键是根据中位线得出规律进行解答．　三、解答题（本大题共9小题，满分58分） 15．（5分）化简求值：[ ﹣]• ，其中x= +1．【考点】6D：分式的化简求值．菁优网版权所有【分析】首先将中括号内的部分进行通分，然后按照同分母分式的减法法则进行计算，再按照分式的乘法法则计算、化简，最后再代数求值即可．【解答】解：原式= ==，将x= +1代入得：原式= =．第16页（共27页）【点评】本题主要考查的是分式的化简以及二次根式的运算，掌握分式的通分、加减、乘除等运算法则是解题的关键． 16．（5分）如图，∠B=∠D，请添加一个条件（不得添加辅助线），使得△AB C≌△ADC，并说明理由．【考点】KB：全等三角形的判定．菁优网版权所有【专题】26：开放型．【分析】已知这两个三角形的一个边与一个角相等，所以再添加一个对应角相等即可．【解答】解：添加∠BAC=∠DAC．理由如下：在△ABC与△ADC中，，∴△ABC≌△ADC（AAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角． 17．（7分）为有效开展阳光体育活动，云洱中学利用课外活动时间进行班级篮球比赛，每场比赛都要决出胜负，每队胜一场得2分，负一场得1分．已知九年级一班在8场比赛中得到13分，问九年级一班胜、负场数分别是多少？第17页（共27页）【考点】8A：一元一次方程的应用．菁优网版权所有【分析】设胜了x场，那么负了（8﹣x）场，根据得分为13分可列方程求解．【解答】解：设胜了x场，那么负了（8﹣x）场，根据题意得： 2x+1•（8﹣x）=13， x=5， 8﹣5=3．答：九年级一班胜、负场数分别是5和3．【点评】本题考查了一元一次方程的应用，还考查了学生的理解题意能力，关键设出胜的场数，以总分数做为等量关系列方程求解． 18．（5分）已知A，B两地相距200千米，一辆汽车以每小时60千米的速度从A 地匀速驶往B地，到达B地后不再行驶，设汽车行驶的时间为x小时，汽车与B 地的距离为y千米．（1）求y与x的函数关系，并写出自变量x的取值范围；（2）当汽车行驶了2小时时，求汽车距B地有多少千米？【考点】FH：一次函数的应用．菁优网版权所有【分析】（1）根据剩余的路程=两地的距离﹣行驶的距离即可得到y与x的函数关系式，然后再求得汽车行驶200千米所需要的时间即可求得x的取值范围．（2）将x=2代入函数关系式，求得y值即可．【解答】解：（1）y=200﹣60x（0≤x≤ ）；（2）将x=2代入函数关系式得：y=200﹣60×2=80千米．答：汽车距离B地80千米．【点评】本题主要考查的是列函数关系式，读懂题意，明确剩余的路程=两地的第18页（共27页）距离﹣行驶的距离是解答本题的关键． 19．（6分）为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据： ≈1.41， ≈1.73，结果保留整数）【考点】T8：解直角三角形的应用．菁优网版权所有【分析】如图，过点C作CD⊥AB于点D，通过解直角△ACD和直角△BCD来求CD 的长度．【解答】解：如图，过点C作CD⊥AB于点D，设CD=x． ∵在直角△ACD中，∠CAD=30°， ∴AD= =x．同理，在直角△BCD中，BD= =x．又∵AB=30米， ∴AD+BD=30米，即 x+ x=30．解得x=13．答：河的宽度的13米．第19页（共27页）【点评】本题考查了解直角三角形的应用．关键把实际问题转化为数学问题加以计算． 20．（7分）现有一个六面分别标有数字1，2，3，4，5，6且质地均匀的正方形骰子，另有三张正面分别标有数字1，2，3的卡片（卡片除数字外，其他都相同），先由小明投骰子一次，记下骰子向上一面出现的数字，然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张，记下卡片上的数字．（1）请用列表或画树形图（树状图）的方法，求出骰子向上一面出现的数字与卡片上的数字之积为6的概率；（2）小明和小王做游戏，约定游戏规则如下：若骰子向上一面出现的数字与卡片上的数字之积大于7，则小明赢；若骰子向上一面出现的数字与卡片上的数字之积小于7，则小王赢，问小明和小王谁赢的可能性更大？请说明理由．【考点】X6：列表法与树状图法；X7：游戏公平性．菁优网版权所有【分析】（1）列举出所有情况，看向上一面出现的数字与卡片上的数字之积为 6的情况数占总情况数的多少即可．（2）概率问题中的公平性问题，解题的关键是计算出各种情况的概率，然后比较即可．【解答】解：（1）如图所示：共18种情况，数字之积为6的情况数有3种，P（数字之积为6） == ．（2）由上表可知，该游戏所有可能的结果共18种，其中骰子向上一面出现的数第20页（共27页）字与卡片上的数字之积大于7的有7种，骰子向上一面出现的数字与卡片上的数字之积小于7的有11种，所以小明赢的概率= ，小王赢的概率= ，故小王赢的可能性更大．【点评】本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平．用到的知识点为：概率= 所求情况数与总情况数之比． 21．（7分）2015年某省为加快建设综合交通体系，对铁路、公路、机场三个重大项目加大了建设资金的投入．（1）机场建设项目中所有6个机场投入的建设资金金额统计如图1，已知机场E 投入的建设资金金额是机场C，D所投入建设资金金额之和的三分之二，求机场E投入的建设资金金额是多少亿元？并补全条形统计图；（2）将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表，根据扇形统计图及统计表中信息，求得a=　170　，b=　30　，c　60%　，d　122.4°　，m　=500　．（请直接填写计算结果）铁路公路机场铁路、公路、机场三项投入建设资金总金额（亿元） 300 abm投入资金（亿元）第21页（共27页） c34% d6% 所占百分比所占圆心角 216° 21.6° 【考点】VA：统计表；VB：扇形统计图；VC：条形统计图．菁优网版权所有【分析】（1）由机场E投入的建设资金金额是机场C，D所投入建设资金金额之和的三分之二，即可得到结果；（2）根据扇形统计图及统计表中提供的信息，列式计算即可得到结果．【解答】解：（1）（2+4）× =4，答：机场E投入的建设资金金额是4亿元，如图所示：（2）c=1﹣34%﹣6%=60%，300÷（1﹣34%﹣6%）=500（亿） a=500×34%=170（亿）， b=500×6%=30（亿）， d=360°﹣216°﹣21.6°=122.4°， m=300+170+30=500（亿）．故答案为：170，30，60%，122.4°，500．【点评】本题主要考查了条形统计图与扇形统计图的应用，根据图象得出正确的信息是解题关键． 22．（7分）如图，在矩形ABCD中，AB=4，AD=6，M，N分别是AB，CD的中点第22页（共27页），P是AD上的点，且∠PNB=3∠CBN．（1）求证：∠PNM=2∠CBN；（2）求线段AP的长．【考点】KD：全等三角形的判定与性质；KF：角平分线的性质；LB：矩形的性质．菁优网版权所有【专题】11：计算题．【分析】（1）由MN∥BC，易得∠CBN=∠MNB，由已知∠PNB=3∠CBN，根据角的和差不难得出结论；（2）连接AN，根据矩形的轴对称性，可知∠PAN=∠CBN，由（1）知∠PNM=2 ∠CBN=2∠PAN，由AD∥MN，可知∠PAN=∠ANM，所以∠PAN=∠PNA，根据等角对等边得到AP=PN，再用勾股定理列方程求出AP．【解答】解：（1）∵四边形ABCD是矩形，M，N分别是AB，CD的中点， ∴MN∥BC， ∴∠CBN=∠MNB， ∵∠PNB=3∠CBN， ∴∠PNM=2∠CBN；（2）连接AN，根据矩形的轴对称性，可知∠PAN=∠CBN， ∵MN∥AD， ∴∠PAN=∠ANM，由（1）知∠PNM=2∠CBN， ∴∠PAN=∠PNA，第23页（共27页） ∴AP=PN， ∵AB=CD=4，M，N分别为AB，CD的中点， ∴DN=2，设AP=x，则PD=6﹣x，在Rt△PDN中 PD2+DN2=PN2， ∴（6﹣x）2+22=x2，解得：x= 所以AP= ．【点评】本题主要考查了矩形的性质、平行线的性质、等腰三角形的判定与性质、勾股定理的综合运用，难度不大，根据角的倍差关系得到∠PAN=∠PNA ，发现AP=PN是解决问题的关键． 23．（9分）如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A （1，0），C（0，3），且BC=5．（1）分别求直线BC和抛物线的解析式（关系式）；（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．第24页（共27页）【考点】HF：二次函数综合题．菁优网版权所有【专题】16：压轴题．【分析】（1）由C的坐标确定出OC的长，在直角三角形BOC中，利用勾股定理求出OB的长，确定出点B坐标，把B与C坐标代入直线解析式求出k与n的值，确定出直线BC解析式，把A与B坐标代入抛物线解析式求出a的值，确定出抛物线解析式即可；（2）在抛物线的对称轴上不存在点P，使得以B，C，P三点为顶点的三角形是直角三角形，如图所示，分两种情况考虑：当PC⊥CB时，△PBC为直角三角形；当P′B⊥BC时，△BCP′为直角三角形，分别求出P的坐标即可．【解答】解：（1）∵C（0，3），即OC=3，BC=5， ∴在Rt△BOC中，根据勾股定理得：OB= 把B与C坐标代入y=kx+n中，得：解得：k=﹣ ，n=3， =4，即B（4，0），，∴直线BC解析式为y=﹣ x+3；由A（1，0），B（4，0），设抛物线解析式为y=a（x﹣1）（x﹣4）=ax2﹣5ax+ 4a，把C（0，3）代入得：a= ，第25页（共27页）则抛物线解析式为y= x2﹣ x+3；（2）存在．如图所示，分两种情况考虑： ∵抛物线解析式为y= x2﹣ x+3， ∴其对称轴x=﹣ =﹣ = ．当P1C⊥CB时，△P1BC为直角三角形， ∵直线BC的斜率为﹣ ， ∴直线P1C斜率为， ∴直线P1C解析式为y﹣3= x，即y= x+3，与抛物线对称轴方程联立得，解得：，此时P（，）；当P2B⊥BC时，△BCP2为直角三角形，同理得到直线P2B的斜率为， ∴直线P2B方程为y= （x﹣4）= x﹣ ，与抛物线对称轴方程联立得：，解得：，第26页（共27页）此时P2（，﹣2）．综上所示，P1（，）或P2（，﹣2）．当点P为直角顶点时，设P（，y）， ∵B（4，0），C（0，3）， ∴BC=5， ∴BC2=PC2+PB2，即25=（）2+（y﹣3）2+（ ﹣4）2+y2，解得y= ，∴P3（，），P4（，）．综上所述，P1（，），P2（，﹣2），P3（，），P4（，）．【点评】此题考查的是二次函数综合题，涉及的知识有：坐标与图形性质，待定系数法确定函数解析式，二次函数的性质，以及两直线垂直时斜率的关系，熟练掌握待定系数法是解本题的关键．　第27页（共27页）