2014年浙江省杭州市中考数学试卷（含解析版）

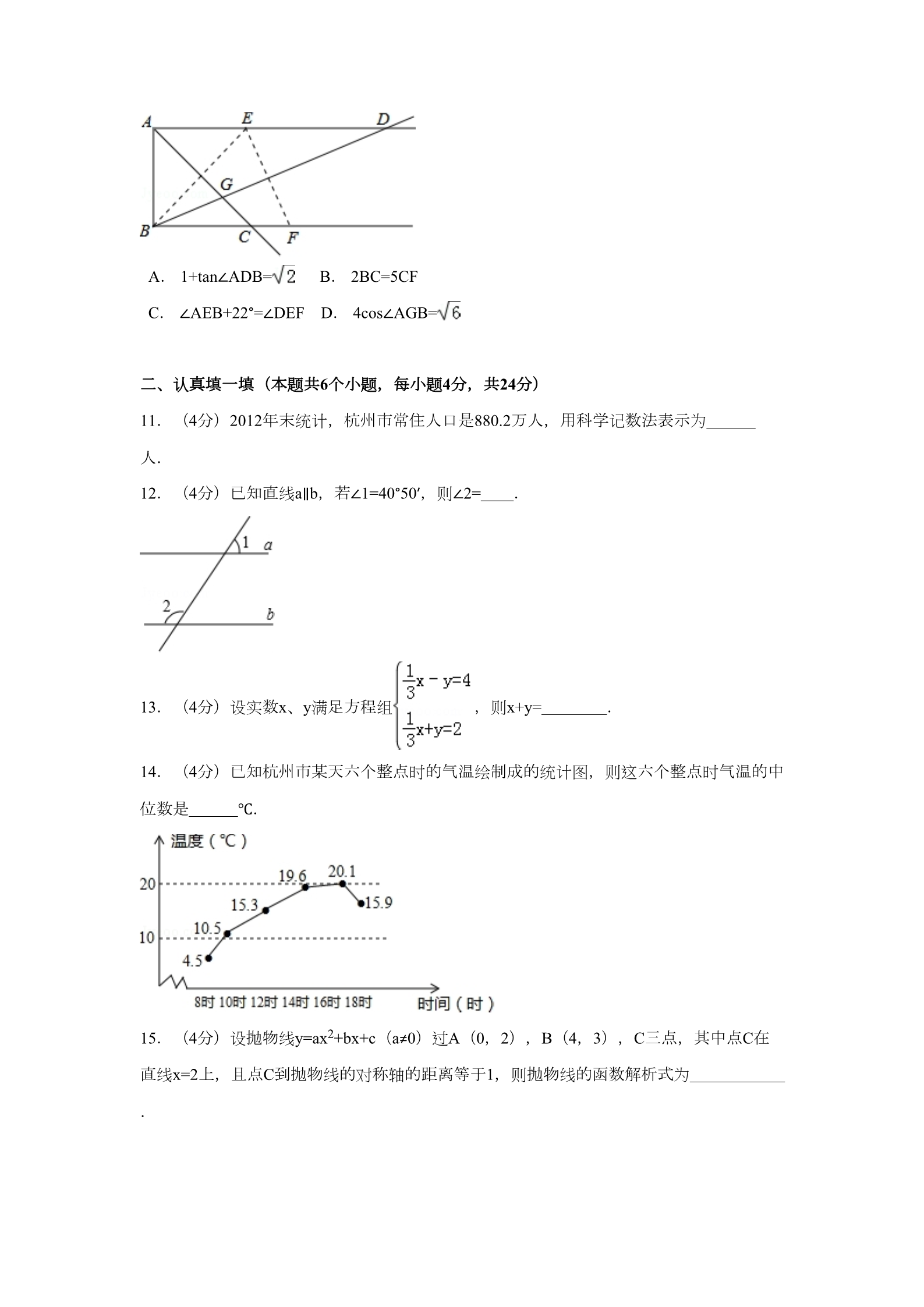
2014年杭州市中考数学试卷一、仔细选一选（本题有10个小题，每小题3分，共30分） 1．（3分）3a•（﹣2a）2=（　　） ﹣12a3 ﹣6a2 33　A． B． C． D． 6a 12a 2．（3分）已知一个圆锥体的三视图如图所示，则这个圆锥的侧面积为（　　） 2222　A． B． C． D． 30πcm 12πcm 15πcm 24πcm 3．（3分）在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC=（　　） 3sin40° 3sin50° 3tan40° 3tan50° D．　A． B． C． 4．（3分）已知边长为a的正方形的面积为8，则下列说法中，错误的是（　　） B． a是方程x2﹣8=0的解　 A． a是无理数　 C． a是8的算术平方根 D． a满足不等式组 5．（3分）下列命题中，正确的是（　　）梯形的对角线相等菱形的对角线不相等　A．　C． B． D．矩形的对角线不能相互垂直平行四边形的对角线可以互相垂直 6．（3分）函数的自变量x满足 ≤x≤2时，函数值y满足 ≤y≤1，则这个函数可以是（　　）　A． B． +C． D． y= y= y= y= 7．（3分）若（）•w=1，则w=（　　） a+2（a≠﹣2） ﹣a+2（a≠2） a﹣2（a≠2） C． ﹣a﹣2（a≠﹣2）　A． B． D． 8．（3分）已知2001年至2012年杭州市小学学校数量（单位：所）和在校学生人数（单位：人）的两幅统计图．由图得出如下四个结论： ①学校数量2007年～2012年比2001～2006年更稳定；②在校学生人数有两次连续下降，两次连续增长的变化过程；③2009年的大于1000； ④2009～2012年，相邻两年的学校数量增长和在校学生人数增长最快的都是2011～2012年．其中，正确的结论是（　　） ①②③④ ①②③ ①② ③④ D．　A． B． C． 9．（3分）让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于（　　）　A． B． C． D． 10．（3分）已知AD∥BC，AB⊥AD，点E，点F分别在射线AD，射线BC上．若点E与点B关于AC对称，点E与点F关于BD对称，AC与BD相交于点G，则（　　） A． 1+tan∠ADB= B． 2BC=5CF C． ∠AEB+22°=∠DEF D． 4cos∠AGB= 二、认真填一填（本题共6个小题，每小题4分，共24分） 11．（4分）2012年末统计，杭州市常住人口是880.2万人，用科学记数法表示为　　人． 12．（4分）已知直线a∥b，若∠1=40°50′，则∠2=　．13．（4分）设实数x、y满足方程组，则x+y=　　． 14．（4分）已知杭州市某天六个整点时的气温绘制成的统计图，则这六个整点时气温的中位数是　℃． 15．（4分）设抛物线y=ax2+bx+c（a≠0）过A（0，2），B（4，3），C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为　　　　．16．（4分）点A，B，C都在半径为r的圆上，直线AD⊥直线BC，垂足为D，直线BE⊥直线 AC，垂足为E，直线AD与BE相交于点H．若BH= AC，则∠ABC所对的弧长等于　（长度单位）．　　三、全面答一答（本题共7小题，共66分）解答应写出文字说明，证明过程或演算步骤，如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以． 17．（6分）一个布袋中装有只有颜色不同的a（a＞12）个球，分别是2个白球，4个黑球， 6个红球和b个黄球，从中任意摸出一个球，把摸出白球，黑球，红球的概率绘制成统计图（未绘制完整）．请补全该统计图并求出的值． 18．（8分）在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点 P．求证：PB=PC，并直接写出图中其他相等的线段．　19．（8分）设y=kx，是否存在实数k，使得代数式（x2﹣y2）（4×2﹣y2）+3×2（4×2﹣y2）能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．　20．（10分）把一条12个单位长度的线段分成三条线段，其中一条线段成为4个单位长度，另两条线段长都是单位长度的整数倍．（1）不同分段得到的三条线段能组成多少个不全等的三角形？用直尺和圆规作这些三角形（用给定的单位长度，不写作法，保留作图痕迹）；（2）求出（1）中所作三角形外接圆的周长．　21．（10分）在直角坐标系中，设x轴为直线l，函数y=﹣ x，y= x的图象分别是直线l1 ，l2，圆P（以点P为圆心，1为半径）与直线l，l1，l2中的两条相切．例如（，1）是其中一个圆P的圆心坐标．（1）写出其余满足条件的圆P的圆心坐标；（2）在图中标出所有圆心，并用线段依次连接各圆心，求所得几何图形的周长． 22．（12分）菱形ABCD的对角线AC，BD相交于点O，AC=4 ，BD=4，动点P在线段B D上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形QEDH与四边形P EBG关于AC对称．设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x．（1）用含x的代数式分别表示S1，S2；（2）若S1=S2，求x的值．　23．（12分）复习课中，教师给出关于x的函数y=2kx2﹣（4kx+1）x﹣k+1（k是实数）．教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上．学生思考后，黑板上出现了一些结论．教师作为活动一员，又补充一些结论，并从中选出以下四条： ①存在函数，其图象经过（1，0）点； ②函数图象与坐标轴总有三个不同的交点； ③当x＞1时，不是y随x的增大而增大就是y随x的增大而减小； ④若函数有最大值，则最大值比为正数，若函数有最小值，则最小值比为负数．教师：请你分别判断四条结论的真假，并给出理由．最后简单写出解决问题时所用的数学方法．　2014年杭州市中考数学试卷　参考答案与试题解析一、仔细选一选（本题有10个小题，每小题3分，共30分） 1．（3分）3a•（﹣2a）2=（　　） ﹣12a3 ﹣6a2 33　A． B． C． D． 6a 12a 单项式乘单项式；幂的乘方与积的乘方．考点：首先利用积的乘方将括号展开，进而利用单项式乘以单项式求出即可．分析：解：3a•（﹣2a）2=3a×4a2=12a3．故选：C．解答：点评此题主要考查了单项式乘以单项式以及积的乘方运算等知识，熟练掌握单项式乘以单项式运算是解题关键．：　2．（3分）已知一个圆锥体的三视图如图所示，则这个圆锥的侧面积为（　　） 2222　A． B． C． D． 30πcm 12πcm 15πcm 24πcm 圆锥的计算计算题．考点：专题：俯视图为圆的只有圆锥，圆柱，球，根据主视图和左视图都是三角形可得到此几何分析：体为圆锥，那么侧面积=底面周长×母线长÷2．解：∵底面半径为3，高为4， ∴圆锥母线长为5，解答：∴侧面积=2πrR÷2=15πcm2．故选B．点评由该三视图中的数据确定圆锥的底面直径和高是解本题的关键；本题体现了数形结合的数学思想，注意圆锥的高，母线长，底面半径组成直角三角形．：　3．（3分）在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC=（　　） 3sin40° 3sin50° 3tan40° 3tan50° 　A． B． C． D．考点解直角三角形：利用直角三角形两锐角互余求得∠B的度数，然后根据正切函数的定义即可求解．解：∠B=90°﹣∠A=90°﹣40°=50°，分析：解答：又∵tanB= ，∴AC=BC•tanB=3tan50°．故选D．点评本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．：　4．（3分）已知边长为a的正方形的面积为8，则下列说法中，错误的是（　　） a是方程x2﹣8=0的解　A．a是无理数 B． D． a是8的算术平方根　C． a满足不等式组算术平方根；无理数；解一元二次方程-直接开平方法；解一元一次不等式组．菁优网版权所有考点：首先根据正方形的面积公式求得a的值，然后根据算术平方根以及方程的解的定义即分析：可作出判断．解：a= =2 ，则a是a是无理数，a是方程x2﹣8=0的解，是8的算术平方根都正确解答：；解不等式组故选D．，得：3＜a＜4，而2 ＜3，故错误．点评此题主要考查了算术平方根的定义，方程的解的定义，以及无理数估计大小的方法：　．5．（3分）下列命题中，正确的是（　　）梯形的对角线相等菱形的对角线不相等　A．　C． B． D．矩形的对角线不能相互垂直平行四边形的对角线可以互相垂直命题与定理．常规题型．考点：专题：根据等腰梯形的判定与性质对A进行判断；根据菱形的性质对B进行判断；根据矩形的性质对C进行判断；根据平行四边形的性质对D进行判断．解：A、等腰梯形的对角线相等，所以A选项错误；分析：解答：B、菱形的对角线不一定相等，若相等，则菱形变为正方形，所以B选项错误； C、矩形的对角线不一定相互垂直，若互相垂直，则矩形变为正方形，所以C选项错误； D、平行四边形的对角线可以互相垂直，此时平行四边形变为菱形，所以D选项正确．故选D．点评本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式；有些命题的正确性是用推理证实的，这样的真命题叫做定理．：　6．（3分）函数的自变量x满足 ≤x≤2时，函数值y满足 ≤y≤1，则这个函数可以是（　　）　A． B． C． D． y= y= y= y= 反比例函数的性质．考点：分析：把x= 代入四个选项中的解析式可得y的值，再把x=2代入解析式可得y的值，然后可得答案．解答：解：A、把x= 代入y= 可得y=1，把x=2代入y= 可得y= ，故此选项正确； B、把x= 代入y= 可得y=4，把x=2代入y= 可得y=1，故此选项错误； C、把x= 代入y= 可得y= ，把x=2代入y= 可得y= ，故此选项错误； D、把x= 代入y= 可得y=16，把x=2代入y= 可得y=4，故此选项错误；故选：A．点评此题主要考查了反比例函数图象的性质，关键是正确理解题意，根据自变量的值求出对应的函数值．：　7．（3分）若（ +）•w=1，则w=（　　） a+2（a≠﹣2） ﹣a+2（a≠2） a﹣2（a≠2） ﹣a﹣2（a≠﹣2） D．　A． B． C．考点分式的混合运算：专题：计算题．原式变形后，计算即可确定出W．解：根据题意得：W= 分析：解答：==﹣（a+2）=﹣a﹣2．故选：D．点评此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．：　8．（3分）已知2001年至2012年杭州市小学学校数量（单位：所）和在校学生人数（单位：人）的两幅统计图．由图得出如下四个结论： ①学校数量2007年～2012年比2001～2006年更稳定； ②在校学生人数有两次连续下降，两次连续增长的变化过程； ③2009年的大于1000； ④2009～2012年，相邻两年的学校数量增长和在校学生人数增长最快的都是2011～2012年．其中，正确的结论是（　　） ①②③④ ①②③ ①② ③④ D．　A． B． C．折线统计图；条形统计图．考点：①根据条形统计图可知，学校数量2001～2006年下降幅度较大，最多1354所，最少 605所，而2007年～2012年学校数量都是在400所以上，440所以下，由此判断即可；分析：②由折线统计图可知，在校学生人数有2001年～2003年、2006年～2009年两次连续下降，2004年～2006年、2009年～2012年两次连续增长的变化过程，由此判断即可；③由统计图可知，2009年的在校学生445192人，学校数量417所，再进行计算即可判断； ④分别计算2009～2010年，2010～2011年，2011～2012年相邻两年的学校数量的增长率和在校学生人数的增长率，再比较即可．解：①根据条形统计图可知，学校数量2001～2006年下降幅度较大，最多1354所，最少605所，而2007年～2012年学校数量都是在400所以上，440所以下，故结论正确；解答：②由折线统计图可知，在校学生人数有2001年～2003年、2006年～2009年两次连续下降，2004年～2006年、2009年～2012年两次连续增长的变化过程，故结论正确； ③由统计图可知，2009年的在校学生445192人，学校数量417所，所以2009年的 ==1067 ＞1000，故结论正确； ④∵2009～2010年学校数量增长率为 2010～2011年学校数量增长率为 ≈﹣2.16%， ≈0.245%， ≈1.47%， 2011～2012年学校数量增长率为 1.47%＞0.245%＞﹣2.16%， ∴2009～2012年，相邻两年的学校数量增长最快的是2011～2012年； ∵2009～2010年在校学生人数增长率为 2010～2011年在校学生人数增长率为 ≈1.96%， ≈2.510%， ≈1.574%， 2011～2012年在校学生人数增长率为 2.510%＞1.96%＞1.574%， ∴2009～2012年，相邻两年的在校学生人数增长最快的是2010～2011年，故结论错误．综上所述，正确的结论是：①②③．故选B．点评本题考查的是条形统计图和折线统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据，折线统计图表示的是事物的变化情况．：　9．（3分）让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于（　　）　A． B． C． D．列表法与树状图法．计算题．考点：专题：分析列表得出所有等可能的情况数，找出两个数的和是2的倍数或3的倍数情况，即可求出所求概率．：解答解：列表如下：：ꢀ1 ꢀ2 ꢀ3 ꢀ4 ꢀ1 ꢀ2 ꢀ3 ꢀ4 ꢀ（1，1） ꢀ（1，2） ꢀ（1，3） ꢀ（1，4） ꢀ（2，1） ꢀ（2，2） ꢀ（2，3） ꢀ（2，4） ꢀ（3，1） ꢀ（3，2） ꢀ（3，3） ꢀ（3，4） ꢀ（4，1） ꢀ（4，2） ꢀ（4，3） ꢀ（4，4）所有等可能的情况有16种，其中两个数的和是2的倍数或3的倍数情况有10种，则P= =．故选C 点评此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比：　．10．（3分）已知AD∥BC，AB⊥AD，点E，点F分别在射线AD，射线BC上．若点E与点B关于AC对称，点E与点F关于BD对称，AC与BD相交于点G，则（　　） ∠AEB+22°=∠DEF D． 4cos∠AGB= 　A． B．2BC=5CF 轴对称的性质；解直角三角形． C． 1+tan∠ADB= 考点：连接CE，设EF与BD相交于点O，根据轴对称性可得AB=AE，并设为1，利用勾股定理列式求出BE，再根据翻折的性质可得DE=BF=BE，再求出BC=1，然后对各选项分析判断利用排除法求解．分析：解：如图，连接CE，设EF与BD相交于点O，解答：由轴对称性得，AB=AE，设为1，则BE= =，∵点E与点F关于BD对称， ∴DE=BF=BE= ∴AD=1+ ，，∵AD∥BC，AB⊥AD，AB=AE， ∴四边形ABCE是正方形， ∴BC=AB=1， 1+tan∠ADB=1+ =1+ ﹣1= ，故A选项结论正确； CF=BF﹣BC= ﹣1， ∴2BC=2×1=2， 5CF=5（ ﹣1）， ∴2BC≠5CF，故B选项结论错误； ∠AEB+22°=45°+22°=67°，在Rt△ABD中，BD= ==，sin∠DEF= ==，∴∠DEF≠67°，故C选项结论错误；由勾股定理得，OE2=（）2﹣（）2= ，∴OE= ，∵∠EBG+∠AGB=90°， ∠EGB+∠BEF=90°， ∴∠AGB=∠BEF，又∵∠BEF=∠DEF， ∴4cos∠AGB= 故选A． ==，故D选项结论错误．点评本题考查了轴对称的性质，解直角三角形，等腰直角三角形的判定与性质，正方形的判定与性质，熟记性质是解题的关键，设出边长为1可使求解过程更容易理解．：　二、认真填一填（本题共6个小题，每小题4分，共24分） 11．（4分）2012年末统计，杭州市常住人口是880.2万人，用科学记数法表示为　 8.802×106　人．科学记数法—表示较大的数．菁优网版权所有考点：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．分析：解：880.2万=880 2000=8.802×106，故答案为：8.802×106．解答：点评此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a| ＜10，n为整数，表示时关键要正确确定a的值以及n的值．：　12．（4分）已知直线a∥b，若∠1=40°50′，则∠2=　139°10′　．平行线的性质；度分秒的换算．菁优网版权所有考点：根据对顶角相等可得∠3=∠1，再根据两直线平行，同旁内角互补列式计算即可得解分析：．解答解：∠3=∠1=40°50′，：∵a∥b， ∴∠2=180°﹣∠3=180°﹣40°50′=139°10′．故答案为：139°10′．点评本题考查了平行线的性质，对顶角相等的性质，度分秒的换算，要注意度、分、秒是60进制．：　13．（4分）设实数x、y满足方程组，则x+y=　8　．解二元一次方程组．菁优网版权所有考点：专题计算题．：方程组利用加减消元法求出解得到x与y的值，即可确定出x+y的值．分析：解答：解：，①+②得： x=6，即x=9； ①﹣②得：﹣2y=2，即y=﹣1， ∴方程组的解为，则x+y=9﹣1=8．故答案为：8 点评此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与：　加减消元法． 14．（4分）已知杭州市某天六个整点时的气温绘制成的统计图，则这六个整点时气温的中位数是　15.6　℃．折线统计图；中位数．菁优网版权所有考点：根据中位数的定义解答．将这组数据从小到大重新排列，求出最中间两个数的平均数即可．分析：解：把这些数从小到大排列为：4.5，10.5，15.3，15.9，19.6，20.1，最中间的两个数的平均数是（15.3+15.9）÷2=15.6（℃），则这六个整点时气温的中位数是15.6℃；解答：故答案为：15.6．点评此题考查了折线统计图和中位数，掌握中位数的定义是本题的关键，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数），叫做这组数据的中位数．：　15．（4分）设抛物线y=ax2+bx+c（a≠0）过A（0，2），B（4，3），C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为　 y= x2﹣ x+2或y=﹣ x2+ x+2　．二次函数图象上点的坐标特征；待定系数法求二次函数解析式．菁优网版权所有考点：根据点C的位置分情况确定出对称轴解析式，然后设出抛物线解析式，再把点A、B 的坐标代入求解即可．分析：解：∵点C在直线x=2上，且到抛物线的对称轴的距离等于1， ∴抛物线的对称轴为直线x=1或x=3，解答：当对称轴为直线x=1时，设抛物线解析式为y=a（x﹣1）2+k，则，解得，所以，y= （x﹣1）2+ =x2﹣ x+2，当对称轴为直线x=3时，设抛物线解析式为y=a（x﹣3）2+k，则，解得，所以，y=﹣ （x﹣3）2+ =﹣ x2+ x+2，综上所述，抛物线的函数解析式为y= x2﹣ x+2或y=﹣ x2+ x+2．故答案为：y= x2﹣ x+2或y=﹣ x2+ x+2．点评本题考查了二次函数图象上点的坐标特征，待定系数法求二次函数解析式，难点在于分情况确定出对称轴解析式并讨论求解．：　16．（4分）点A，B，C都在半径为r的圆上，直线AD⊥直线BC，垂足为D，直线BE⊥直线 AC，垂足为E，直线AD与BE相交于点H．若BH= AC，则∠ABC所对的弧长等于　 πr或 r　（长度单位）．弧长的计算；圆周角定理；相似三角形的判定与性质；特殊角的三角函数值．菁优网版权所有考点：专题分类讨论．：作出图形，根据同角的余角相等求出∠H=∠C，再根据两角对应相等，两三角形相似求出△ACD和△BHD相似，根据相似三角形对应边成比例列式求出，再利用锐角分析：三角函数求出∠ABC，然后根据在同圆或等圆中，同弧所对的圆心角等于圆周角的2 倍求出∠ABC所对的弧长所对的圆心角，然后利用弧长公式列式计算即可得解．解：如图1，∵AD⊥BC，BE⊥AC， ∴∠H+∠DBH=90°， ∠C+∠DBH=90°，解答：∴∠H=∠C，又∵∠BDH=∠ADC=90°， ∴△ACD∽△BHD， ∴=，∵BH= AC， ∴=，∴∠ABC=30°， ∴∠ABC所对的弧长所对的圆心角为30°×2=60°， ∴∠ABC所对的弧长= = πr．如图2，∠ABC所对的弧长所对的圆心角为300°， ∴∠ABC所对的弧长= 故答案为： πr或 = πr． r．点评本题考查了弧长的计算，圆周角定理，相似三角形的判定与性质，特殊角的三角函数值，判断出相似三角形是解题的关键，作出图形更形象直观．：　三、全面答一答（本题共7小题，共66分）解答应写出文字说明，证明过程或演算步骤，如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以． 17．（6分）一个布袋中装有只有颜色不同的a（a＞12）个球，分别是2个白球，4个黑球， 6个红球和b个黄球，从中任意摸出一个球，把摸出白球，黑球，红球的概率绘制成统计图（未绘制完整）．请补全该统计图并求出的值．条形统计图；概率公式．菁优网版权所有考点：首先根据黑球数÷总数=摸出黑球的频率，再计算出摸出白球，黑球，红球的概率可分析：得答案．解：球的总数：4÷0.2=20（个）， 2+4+6+b=20，解答：解得：b=8，摸出白球频率：2÷20=0.1，摸出红球的概率：6÷20=0.3， == =0.4．点评此题主要考查了概率和条形统计图，关键是掌握概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数．：　18．（8分）在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点 P．求证：PB=PC，并直接写出图中其他相等的线段．全等三角形的判定与性质；等腰三角形的性质．菁优网版权所有考点：可证明△ABF≌△ACE，则BF=CE，再证明△BEP≌△CFP，则PB=PC，从而可得出PE= PF，BE=CF．分析：解答解：在△ABF和△ACE中，：，∴△ABF≌△ACE（SAS）， ∴∠ABF=∠ACE（全等三角形的对应角相等）， ∴BF=CE（全等三角形的对应边相等）， ∵AB=AC，AE=AF， ∴BE=BF，在△BEP和△CFP中，，∴△BEP≌△CFP（AAS）， ∴PB=PC， ∵BF=CE， ∴PE=PF， ∴图中相等的线段为PE=PF，BE=CF．点评本题考查了全等三角形的判定和性质以及等腰三角形的性质，是基础题，难度不大：　．19．（8分）设y=kx，是否存在实数k，使得代数式（x2﹣y2）（4×2﹣y2）+3×2（4×2﹣y2）能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．因式分解的应用．菁优网版权所有考点：专题计算题．：先利用因式分解得到原式=（4×2﹣y2）（x2﹣y2+3×2）=（4×2﹣y2）2，再把当y=kx 代入得到原式=（4×2﹣k2x2）2=（4﹣k2）x4，所以当4﹣k2=1满足条件，然后解关于 k的方程即可．分析：解答解：能．（x2﹣y2）（4×2﹣y2）+3×2（4×2﹣y2）：=（4×2﹣y2）（x2﹣y2+3×2） =（4×2﹣y2）2，当y=kx，原式=（4×2﹣k2x2）2=（4﹣k2）2×4，令（4﹣k2）2=1，解得k=± 或± 即当k=± 或± 时，原代数式可化简为x4．点评本题考查了因式分解的运用：利用因式分解解决求值问题；利用因式分解解决证明，问题；利用因式分解简化计算问题．：　20．（10分）把一条12个单位长度的线段分成三条线段，其中一条线段成为4个单位长度，另两条线段长都是单位长度的整数倍．（1）不同分段得到的三条线段能组成多少个不全等的三角形？用直尺和圆规作这些三角形（用给定的单位长度，不写作法，保留作图痕迹）；（2）求出（1）中所作三角形外接圆的周长．作图—应用与设计作图．菁优网版权所有考点：（1）利用三角形三边关系进而得出符合题意的图形即可；（2）利用三角形外接圆作法，首先作出任意两边的垂直平分线，即可得出圆心位置，进而得出其外接圆．分析：解：（1）由题意得：三角形的三边长分别为：4，4，4；3，4，5；即不同分段得到的三条线段能组成2个不全等的三角形，如图所示：解答：（2）如图所示：当三边的单位长度分别为3，4，5，可知三角形为直角三角形，此时外接圆的半径为 2.5；当三边的单位长度分别为4，4，4．三角形为等边三角形，此时外接圆的半径为，∴当三条线段分别为3，4，5时其外接圆周长为：2π×2.5=5π；当三条线段分别为4，4，4时其外接圆周长为：2π× =π．点评此题主要考查了三角形外接圆的作法和三角形三边关系等知识，得出符合题意的三角形是解题关键．：　21．（10分）在直角坐标系中，设x轴为直线l，函数y=﹣ x，y= x的图象分别是直线l1 ，l2，圆P（以点P为圆心，1为半径）与直线l，l1，l2中的两条相切．例如（，1）是其中一个圆P的圆心坐标．（1）写出其余满足条件的圆P的圆心坐标；（2）在图中标出所有圆心，并用线段依次连接各圆心，求所得几何图形的周长．圆的综合题；切线长定理；轴对称图形；特殊角的三角函数值．菁优网版权所有考点：专题计算题；作图题．：（1）对圆P与直线l和l2都相切、圆P与直线l和l1都相切、圆P与直线l1和l2都相切三种情况分别考虑，利用切线长定理和特殊角的三角函数值即可求出点P的坐标．（2）由图可知：该几何图形既轴对称图形，又是中心对称图形，它的所有的边都相等．只需求出其中的一条边就可以求出它的周长．分析：解：（1）①若圆P与直线l和l2都相切，解答：当点P在第四象限时，过点P作PH⊥x轴，垂足为H，连接OP，如图1所示．设y= x的图象与x轴的夹角为α．当x=1时，y= ．∴tanα= ．∴α=60°． ∴由切线长定理得：∠POH= （180°﹣60°）=60°． ∵PH=1， ∴tan∠POH= ==．∴OH= ．∴点P的坐标为（，﹣1）．同理可得：当点P在第二象限时，点P的坐标为（﹣ ，1）；当点P在第三象限时，点P的坐标为（﹣ ，﹣1）； ②若圆P与直线l和l1都相切，如图2所示．同理可得：当点P在第一象限时，点P的坐标为（，1）；当点P在第二象限时，点P的坐标为（﹣ ，1）；当点P在第三象限时，点P的坐标为（﹣ ，﹣1）；当点P在第四象限时，点P的坐标为（，﹣1）． ③若圆P与直线l1和l2都相切，如图3所示．同理可得：当点P在x轴的正半轴上时，点P的坐标为（当点P在x轴的负半轴上时，点P的坐标为（﹣ ，0）；，0）；当点P在y轴的正半轴上时，点P的坐标为（0，2）；当点P在y轴的负半轴上时，点P的坐标为（0，﹣2）．综上所述：其余满足条件的圆P的圆心坐标有：（（（，﹣1）、（﹣ ，1）、（﹣ ，﹣1）、，1）、（﹣ ，1）、（﹣ ，﹣1）、（，﹣1）、，0）、（﹣ ，0）、（0，2）、（0，﹣2）．（2）用线段依次连接各圆心，所得几何图形，如图4所示．由图可知：该几何图形既轴对称图形，又是中心对称图形，由对称性可得：该几何图形的所有的边都相等． ∴该图形的周长=12×（ ﹣）=8 ．点评本题考查了切线长定理、特殊角的三角函数值、对称性等知识，考查了作图的能力，培养了学生的审美意识，是一道好题．：　22．（12分）菱形ABCD的对角线AC，BD相交于点O，AC=4 ，BD=4，动点P在线段B D上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形QEDH与四边形P EBG关于AC对称．设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x．（1）用含x的代数式分别表示S1，S2；（2）若S1=S2，求x的值．四边形综合题；菱形的性质；轴对称的性质；轴对称图形；特殊角的三角函数值．菁优网版权所有考点：专题综合题；动点型；分类讨论．：（1）根据对称性确定E、F、G、H都在菱形的边上，由于点P在BO上与点P在OD上求S1和S2的方法不同，因此需分情况讨论．分析：（2）由S1=S2和S1+S2=8 可以求出S1=S2=4 ．然后在两种情况下分别建立关于x 的方程，解方程，结合不同情况下x的范围确定x的值．解：（1）①当点P在BO上时，如图1所示． ∵四边形ABCD是菱形，AC=4 ，BD=4，解答：∴AC⊥BD，BO= BD=2，AO= AC=2 且S菱形ABCD= BD•AC=8 ，．∴tan∠ABO= =．∴∠ABO=60°．在Rt△BFP中， ∵∠BFP=90°，∠FBP=60°，BP=x， ∴sin∠FBP= ∴FP= x． ∴BF= ． ==sin60°= ．∵四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称， ∴S△BFP=S△BGP=S△DEQ=S△DHQ ∴S1=4S△BFP ．=4× ×x• =．∴S2=8 ﹣．②当点P在OD上时，如图2所示． ∵AB=4，BF= ， ∴AF=AB﹣BF=4﹣ ．在Rt△AFM中， ∵∠AFM=90°，∠FAM=30°，AF=4﹣ ． ∴tan∠FAM= =tan30°= ∴FM= （4﹣ ）． ∴S△AFM= AF•FM ．= （4﹣ ）• （4﹣ ） =（4﹣ ）2． ∵四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称， ∴S△AFM=S△AEM=S△CHN=S△CGN ∴S2=4S△AFM ．=4× （4﹣ ）2 =（x﹣8）2． ∴S1=8 ﹣S2=8 综上所述： ﹣（x﹣8）2．，S2=8 当点P在BO上时，S1= 当点P在OD上时，S1=8 ﹣；﹣（x﹣8）2，S2= （x﹣8）2．（2）①当点P在BO上时，0＜x≤2． ∵S1=S2，S1+S2=8 ，∴S1=4 ．∴S1= =4 ．解得：x1=2 ，x2=﹣2 ∵2 ＞2，﹣2 ＜0，．∴当点P在BO上时，S1=S2的情况不存在． ②当点P在OD上时，2＜x≤4． ∵S1=S2，S1+S2=8 ∴S2=4 ，．∴S2= （x﹣8）2=4 ．解得：x1=8+2 ，x2=8﹣2 ∵8+2 ＞4，2＜8﹣2 ＜4， ∴x=8﹣2 综上所述：若S1=S2，则x的值为8﹣2 ．．．点评本题考查了以菱形为背景的轴对称及轴对称图形的相关知识，考查了菱形的性质、特殊角的三角函数值等知识，还考查了分类讨论的思想．：　23．（12分）复习课中，教师给出关于x的函数y=2kx2﹣（4kx+1）x﹣k+1（k是实数）．教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上．学生思考后，黑板上出现了一些结论．教师作为活动一员，又补充一些结论，并从中选出以下四条： ①存在函数，其图象经过（1，0）点； ②函数图象与坐标轴总有三个不同的交点； ③当x＞1时，不是y随x的增大而增大就是y随x的增大而减小； ④若函数有最大值，则最大值比为正数，若函数有最小值，则最小值比为负数．教师：请你分别判断四条结论的真假，并给出理由．最后简单写出解决问题时所用的数学方法．二次函数综合题．菁优网版权所有考点：①将（1，0）点代入函数，解出k的值即可作出判断； ②首先考虑，函数为一次函数的情况，从而可判断为假； ③根据二次函数的增减性，即可作出判断； ④当k=0时，函数为一次函数，无最大之和最小值，当k≠0时，函数为抛物线，求出顶点的纵坐标表达式，即可作出判断．分析：解：①真，将（1，0）代入可得：2k﹣（4k+1）﹣k+1=0，解得：k=0．解答：运用方程思想； ②假，反例：k=0时，只有两个交点．运用举反例的方法； ③假，如k=1，﹣ = ，当x＞1时，先减后增；运用举反例的方法； ④真，当k=0时，函数无最大、最小值； k≠0时，y最= =﹣ ，∴当k＞0时，有最小值，最小值为负；当k＜0时，有最大值，最大值为正．运用分类讨论思想．点评本题考查了二次函数的综合，立意新颖，结合考察了数学解题过程中经常用到的几种解题方法，同学们注意思考、理解，难度一般．：