2014年宁夏省中考数学试卷（含解析版）

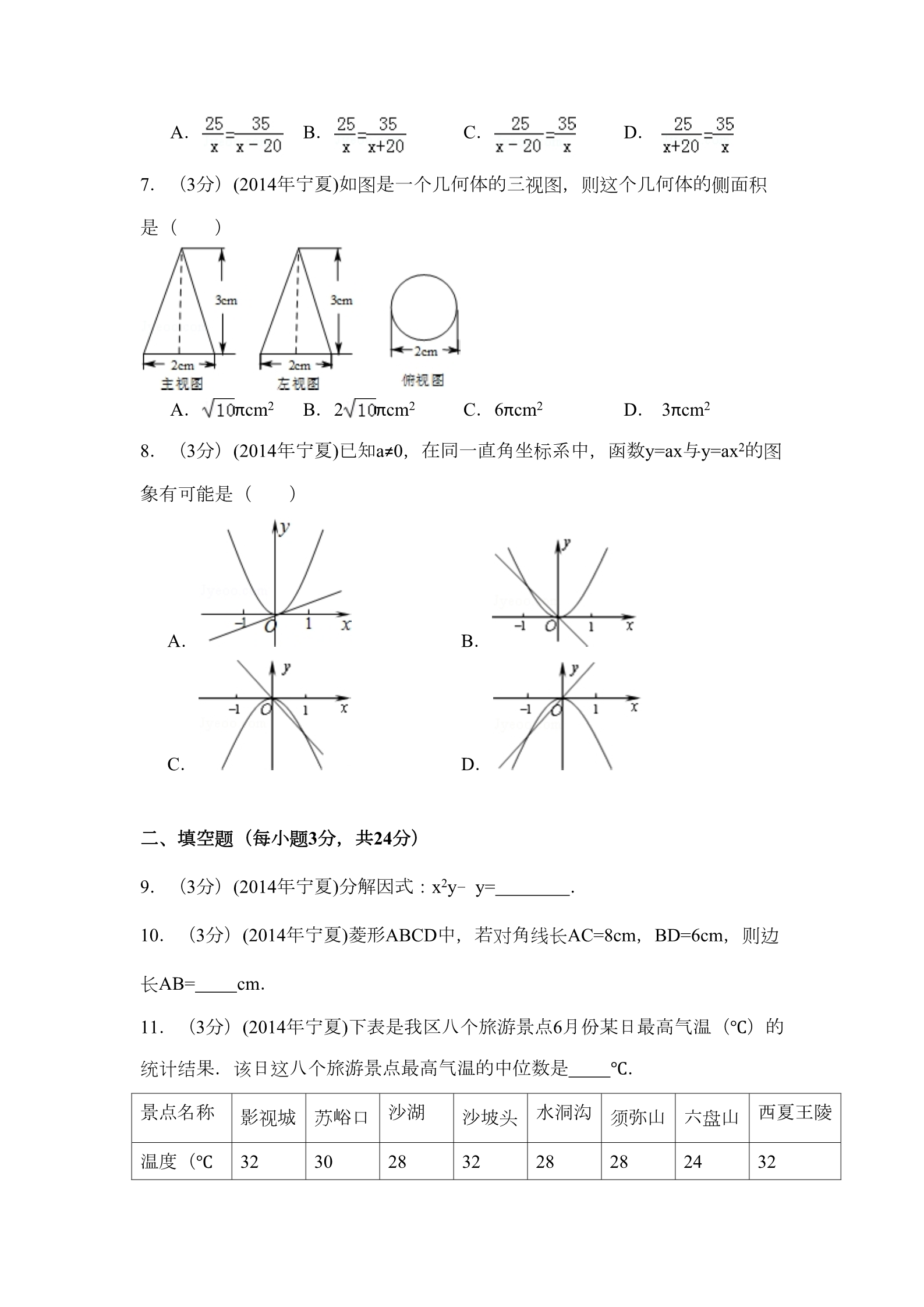
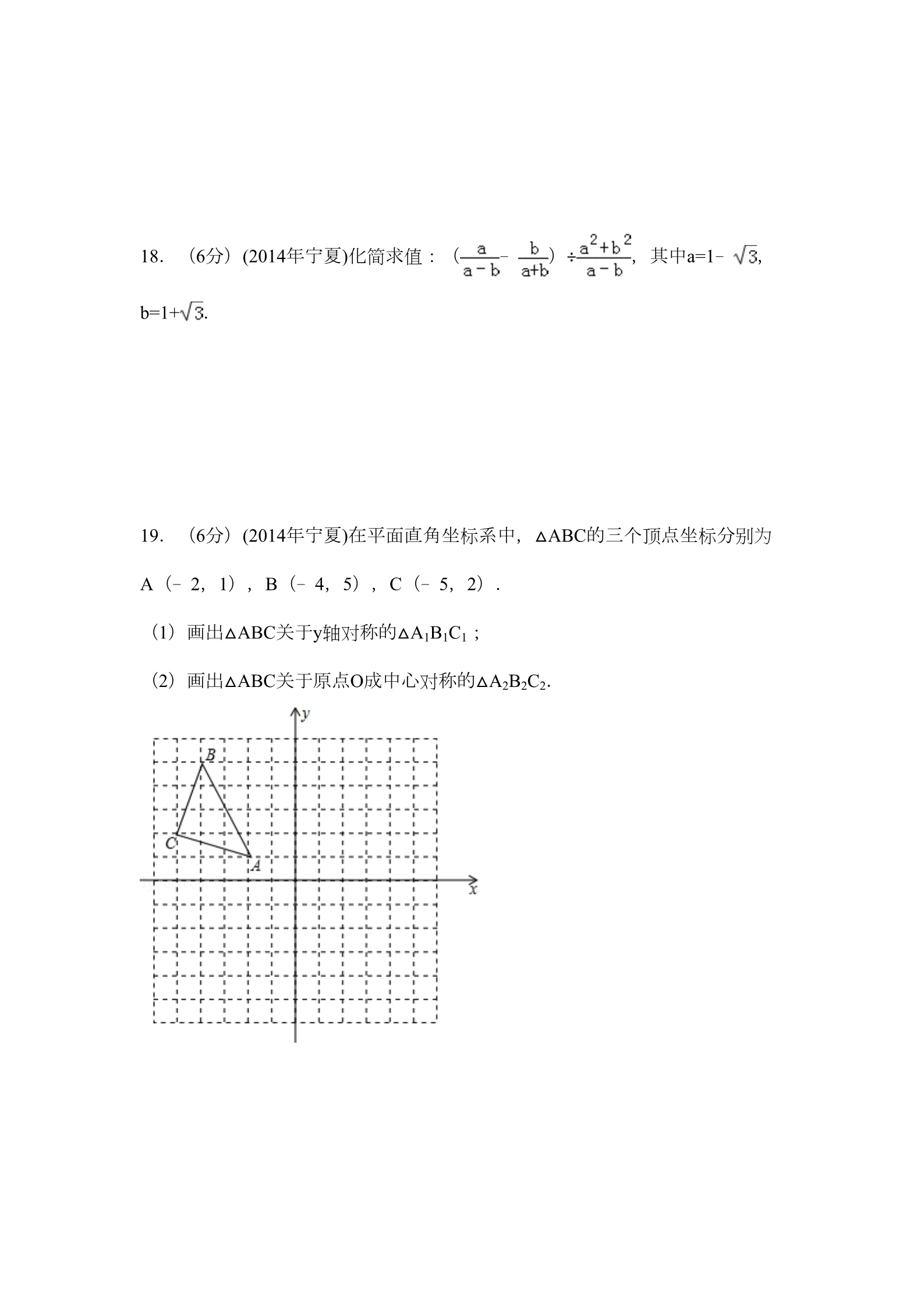
2014年宁夏中考数学试卷一、选择题（下列每小题所给的四个答案中只有一个是正确的，每小题3分，共24分） 1．（3分）(2014年宁夏)下列运算正确的是（　　）　 A．a2•a3=a6 B．a8÷a4=a2 C．a3+a3=2a6 D．（a3）2=a6 2．（3分）(2014年宁夏)已知不等式组，其解集在数轴上表示正确的是（　　）　 A．　 C． B． D． 3．（3分）(2014年宁夏)一元二次方程x2﹣2x﹣1=0的解是（　　）　 A．x1=x2=1 　 B．x1=1+ ，x2=﹣1﹣ 　 C．x1=1+ ，x2=1﹣ D．x1=﹣1+ ，x2=﹣1﹣ 4．（3分）(2014年宁夏)实数a，b在数轴上的位置如图所示，以下说法正确的是（　　）　 A．a+b=0 B．b＜a C．ab＞0 D． |b|＜|a| 5．（3分）(2014年宁夏)已知两点P1（x1，y1）、P2（x2，y2）在函数y= 的图象上，当x1＞x2＞0时，下列结论正确的是（　　）　 A．0＜y1＜y2 B．0＜y2＜y1 C．y1＜y2＜0 D． y2＜y1＜0 6．（3分）(2014年宁夏)甲种污水处理器处理25吨的污水与乙种污水处理器处理35吨的污水所用时间相同，已知乙种污水处理器每小时比甲种污水处理器多处理20吨的污水，求两种污水处理器的污水处理效率．设甲种污水处理器的污水处理效率为x吨/小时，依题意列方程正确的是（　　）　 A． B． C． D． 7．（3分）(2014年宁夏)如图是一个几何体的三视图，则这个几何体的侧面积是（　　）　 A． πcm2 B．2 πcm2 C．6πcm2 D． 3πcm2 8．（3分）(2014年宁夏)已知a≠0，在同一直角坐标系中，函数y=ax与y=ax2的图象有可能是（　　）　 A． B． D．　 C．　二、填空题（每小题3分，共24分） 9．（3分）(2014年宁夏)分解因式：x2y﹣y=　　． 10．（3分）(2014年宁夏)菱形ABCD中，若对角线长AC=8cm，BD=6cm，则边长AB=　 cm． 11．（3分）(2014年宁夏)下表是我区八个旅游景点6月份某日最高气温（℃）的统计结果．该日这八个旅游景点最高气温的中位数是　 ℃．景点名称沙湖水洞沟西夏王陵影视城苏峪口 30 沙坡头须弥山六盘山 28 24 温度（℃ 32 28 32 28 32 ）12．（3分）(2014年宁夏)若2a﹣b=5，a﹣2b=4，则a﹣b的值为　．13．（3分）(2014年宁夏)一个口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸出一个小球，然后放回，再随机地摸出一个小球，则两次摸出的小球标号的和等于4的概率是　．14．（3分）(2014年宁夏)服装店销售某款服装，一件服装的标价为300元，若按标价的八折销售，仍可获利20%，则这款服装每件的进价是　元． 15．（3分）(2014年宁夏)如图，在四边形ABCD中，AD∥BC，AB=CD=2，BC= 5，∠BAD的平分线交BC于点E，且AE∥CD，则四边形ABCD的面积为　． 16．（3分）(2014年宁夏)如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面的半径是　．　三、解答题（共24分） 17．（6分）(2014年宁夏)计算：（﹣ ）﹣2+ ﹣2sin45°﹣|1﹣ |．　18．（6分）(2014年宁夏)化简求值：（ ﹣）÷ ，其中a=1﹣ ，b=1+ ．　19．（6分）(2014年宁夏)在平面直角坐标系中，△ABC的三个顶点坐标分别为 A（﹣2，1），B（﹣4，5），C（﹣5，2）．（1）画出△ABC关于y轴对称的△A1B1C1；（2）画出△ABC关于原点O成中心对称的△A2B2C2．　20．（6分）(2014年宁夏)在△ABC中，AD是BC边上的高，∠C=45°，sinB= ， AD=1．求BC的长．　四、解答题（共48分） 21．（6分）(2014年宁夏)如图是银川市6月1日至15日的空气质量指数趋势折线统计图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气质量重度污染．某人随机选择6月1日至6月14日中的某一天到达银川，共停留2天．（1）求此人到达当天空气质量优良的天数；（2）求此人在银川停留2天期间只有一天空气质量是重度污染的概率；（3）由折线统计图判断从哪天开始连续三天的空气质量指数方差最大（只写结论）．　22．（6分）(2014年宁夏)在平行四边形ABCD中，将△ABC沿AC对折，使点B 落在B′处，A B′和CD相交于点O．求证：OA=OC．　23．（8分）(2014年宁夏)在等边△ABC中，以BC为直径的⊙O与AB交于点D， DE⊥AC，垂足为点E．（1）求证：DE为⊙O的切线；（2）计算．　24．（8分）(2014年宁夏)在平面直角坐标系中，已知反比例函数y= 的图象经过点A（1，）．（1）试确定此反比例函数的解析式；（2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB，判断点B 是否在此反比例函数的图象上，并说明理由．　25．（10分）(2014年宁夏)某花店计划下个月每天购进80只玫瑰花进行销售，若下个月按30天计算，每售出1只玫瑰花获利润5元，未售出的玫瑰花每只亏损3 元．以x（0＜x≤80）表示下个月内每天售出的只数，y（单位：元）表示下个月每天销售玫瑰花的利润．根据历史资料，得到同期下个月内市场销售量的频率分布直方图（每个组距包含左边的数，但不包含右边的数）如图所示：（1）求y关于x的函数关系式；（2）根据频率分布直方图，计算下个月内销售利润少于320元的天数；（3）根据历史资料，在70≤x＜80这个组内的销售情况如下表： 70 172 274 375 477 379 2销售量/只天数计算该组内平均每天销售玫瑰花的只数．　26．（10分）(2014年宁夏)在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．（1）试说明不论点P在BC边上何处时，都有△PBQ与△ABC相似；（2）若AC=3，BC=4，当BP为何值时，△AQP面积最大，并求出最大值；（3）在Rt△ABC中，两条直角边BC、AC满足关系式BC=λAC，是否存在一个λ 的值，使Rt△AQP既与Rt△ACP全等，也与Rt△BQP全等．　2014年宁夏中考数学试卷　参考答案与试题解析一、选择题（下列每小题所给的四个答案中只有一个是正确的，每小题3分，共24分） 1．（3分）(2014年宁夏)下列运算正确的是（　　）　 A．a2•a3=a6 B．a8÷a4=a2 C．a3+a3=2a6 D．（a3）2=a6 【考点】同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．【分析】分别根据合并同类项、同底数幂的乘法和除法、幂的乘方法则进行计算即可．【解答】解：A、a2•a3=a5≠a6，故本选项错误； B、a8÷a4=a4≠a2，故本选项错误； C、a3+a3=2a3≠2a6，故本选项错误； D、（a3）2=a3×2=a6，正确．故选D．【点评】本题考查了合并同类项，同底数幂的乘法，同底数幂的除法，幂的乘方，熟练掌握运算法则是解题的关键，合并同类项时，只把系数相加减，字母与字母的次数不变．　2．（3分）(2014年宁夏)已知不等式组，其解集在数轴上表示正确的是（　　）　 A． B．　 C． D．【考点】在数轴上表示不等式的解集；解一元一次不等式组．【分析】求出每个不等式的解集，找出不等式组的解集，再在数轴上把不等式组的解集表示出来，即可得出选项．【解答】解： ∵解不等式①得：x＞3，解不等式②得：x≥﹣1， ∴不等式组的解集为：x＞3，在数轴上表示不等式组的解集为：故选B．【点评】本题考查了在数轴上表示不等式组的解集，解一元一次不等式（组）的应用，关键是能正确在数轴上表示不等式组的解集．　3．（3分）(2014年宁夏)一元二次方程x2﹣2x﹣1=0的解是（　　）　 A．x1=x2=1 　 B．x1=1+ ，x2=﹣1﹣ 　 C．x1=1+ ，x2=1﹣ 【考点】解一元二次方程-配方法．【专题】计算题． D．x1=﹣1+ ，x2=﹣1﹣ 【分析】方程变形后，配方得到结果，开方即可求出值．【解答】解：方程x2﹣2x﹣1=0，变形得：x2﹣2x=1，配方得：x2﹣2x+1=2，即（x﹣1）2=2，开方得：x﹣1=± ，解得：x1=1+ ，x2=1﹣ 故选C．．【点评】此题考查了解一元二次方程﹣配方法，熟练掌握完全平方公式是解本题的关键．　4．（3分）(2014年宁夏)实数a，b在数轴上的位置如图所示，以下说法正确的是（　　）　 A．a+b=0 B．b＜a C．ab＞0 D． |b|＜|a| 【考点】实数与数轴．【分析】根据图形可知，a是一个负数，并且它的绝对是大于1小于2，b是一个正数，并且它的绝对值是大于0小于1，即可得出|b|＜|a|．【解答】解：根据图形可知： ﹣2＜a＜﹣1， 0＜b＜1，则|b|＜|a|；故选D．【点评】此题主要考查了实数与数轴，解答此题的关键是根据数轴上的任意两个数，右边的数总比左边的数大，负数的绝对值等于它的相反数，正数的绝对值等于本身．　5．（3分）(2014年宁夏)已知两点P1（x1，y1）、P2（x2，y2）在函数y= 的图象上，当x1＞x2＞0时，下列结论正确的是（　　）　 A．0＜y1＜y2 B．0＜y2＜y1 C．y1＜y2＜0 D． y2＜y1＜0 【考点】反比例函数图象上点的坐标特征．【专题】计算题．【分析】根据反比例函数图象上点的坐标特征得y1= ，y2= ，然后利用求差法比较y1与y2的大小．【解答】解：把点P1（x1，y1）、P2（x2，y2）代入y= 得y1= ，y2= ，则y1﹣y2= ﹣=，∵x1＞x2＞0， ∴y1﹣y2= ＜0，即y1＜y2．故选A．【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数y= （k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即x y=k．　6．（3分）(2014年宁夏)甲种污水处理器处理25吨的污水与乙种污水处理器处理35吨的污水所用时间相同，已知乙种污水处理器每小时比甲种污水处理器多处理20吨的污水，求两种污水处理器的污水处理效率．设甲种污水处理器的污水处理效率为x吨/小时，依题意列方程正确的是（　　）　 A． B． C． D．【考点】由实际问题抽象出分式方程．【分析】设甲种污水处理器的污水处理效率为x吨/小时，则乙种污水处理器的污水处理效率为（x+20）吨/小时，根据甲种污水处理器处理25吨的污水与乙种污水处理器处理35吨的污水所用时间相同，列出方程．【解答】解：设甲种污水处理器的污水处理效率为x吨/小时，则乙种污水处理器的污水处理效率为（x+20）吨/小时，由题意得，故选B． =．【点评】本题考查了由实际问题抽象出分式方程，关键是读懂题意，设出未知数，找出合适的等量关系，列出方程．　7．（3分）(2014年宁夏)如图是一个几何体的三视图，则这个几何体的侧面积是（　　）　 A． πcm2 B．2 πcm2 C．6πcm2 D． 3πcm2 【考点】圆锥的计算；由三视图判断几何体．【分析】俯视图为圆的只有圆锥，圆柱，球，根据主视图和左视图都是三角形可得到此几何体为圆锥，那么侧面积=底面周长×母线长÷2．【解答】解：此几何体为圆锥； ∵半径为1cm，高为3cm， ∴圆锥母线长为 cm， ∴侧面积=2πrR÷2= 故选A． πcm2；【点评】本题考查了圆锥的计算，该三视图中的数据确定圆锥的底面直径和高是解本题的关键；本题体现了数形结合的数学思想，注意圆锥的高，母线长，底面半径组成直角三角形．　8．（3分）(2014年宁夏)已知a≠0，在同一直角坐标系中，函数y=ax与y=ax2的图象有可能是（　　）　 A．　 C． B． D．【考点】二次函数的图象；正比例函数的图象．【分析】本题可先由一次函数y=ax图象得到字母系数的正负，再与二次函数y=a x2的图象相比较看是否一致．（也可以先固定二次函数y=ax2图象中a的正负，再与一次函数比较．）【解答】解：A、函数y=ax中，a＞0，y=ax2中，a＞0，但当x=1时，两函数图象有交点（1，a），错误； B、函数y=ax中，a＜0，y=ax2中，a＞0，错误； C、函数y=ax中，a＜0，y=ax2中，a＜0，但当x=1时，两函数图象有交点（1，a ），正确； D、函数y=ax中，a＞0，y=ax2中，a＜0，错误．故选C．【点评】函数中数形结合思想就是：由函数图象确定函数解析式各项系数的性质符号，由函数解析式各项系数的性质符号画出函数图象的大致形状．　二、填空题（每小题3分，共24分） 9．（3分）(2014年宁夏)分解因式：x2y﹣y=　y（x+1）（x﹣1）　．【考点】提公因式法与公式法的综合运用．【分析】观察原式x2y﹣y，找到公因式y后，提出公因式后发现x2﹣1符合平方差公式，利用平方差公式继续分解可得．【解答】解：x2y﹣y， =y（x2﹣1）， =y（x+1）（x﹣1）．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．　10．（3分）(2014年宁夏)菱形ABCD中，若对角线长AC=8cm，BD=6cm，则边长AB=　5　cm．【考点】菱形的性质；勾股定理．【专题】常规题型．【分析】根据菱形的对角线互相垂直平分求出对角线一半的长度，然后利用勾股定理列式计算即可得解．【解答】解：如图，∵菱形ABCD中，对角线长AC=8cm，BD=6cm， ∴AO= AC=4cm，BO= BD=3cm， ∵菱形的对角线互相垂直， ∴在Rt△AOB中，AB= 故答案为：5． ==5cm．【点评】本题主要考查了菱形的对角线互相垂直平分的性质，作出图形更形象直观且有助于理解．　11．（3分）(2014年宁夏)下表是我区八个旅游景点6月份某日最高气温（℃）的统计结果．该日这八个旅游景点最高气温的中位数是　29　℃．景点名称沙湖水洞沟西夏王陵影视城苏峪口沙坡头须弥山六盘山 28 24 温度（℃ 32 ）30 28 32 28 32 【考点】中位数．【分析】根据中位数的概念求解．【解答】解：这组数据按照从小到大的顺序排列为：24，28，28，28，30，32 ，32，32，则中位数为： =29．故答案为：29．【点评】本题考查了中位数的知识，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．　12．（3分）(2014年宁夏)若2a﹣b=5，a﹣2b=4，则a﹣b的值为　3　．【考点】解二元一次方程组．【专题】计算题．【分析】已知两等式左右两边相加，变形即可得到a﹣b的值．【解答】解：将2a﹣b=5，a﹣2b=4，相加得：2a﹣b+a﹣2b=9，即3a﹣3b=9，解得：a﹣b=3．故答案为：3．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．　13．（3分）(2014年宁夏)一个口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸出一个小球，然后放回，再随机地摸出一个小球，则两次摸出的小球标号的和等于4的概率是　．【考点】列表法与树状图法．【专题】计算题．【分析】先画树状图展示所有16种等可能的结果数，其中两次摸出的小球标号的和等于4的占3种，然后根据概率的概念计算即可．【解答】解：如图，随机地摸出一个小球，然后放回，再随机地摸出一个小球，共有16种等可能的结果数，其中两次摸出的小球标号的和等于4的占3种，所有两次摸出的小球标号的和等于4的概率= 故答案为．．【点评】本题考查了列表法或树状图法：利用列表法或树状图法展示所有等可能的结果数n，再找出某事件所占有的结果数m，然后利用概率的概念求得这个事件的概率= ．　14．（3分）(2014年宁夏)服装店销售某款服装，一件服装的标价为300元，若按标价的八折销售，仍可获利20%，则这款服装每件的进价是　200　元．【考点】一元一次方程的应用．【分析】设这款服装每件的进价为x元，根据利润=售价﹣进价建立方程求出x的值就可以求出结论．【解答】解：设这款服装每件的进价为x元，由题意，得 300×0.8﹣x=20%x，解得：x=200．故答案是：200．【点评】本题考查了列一元一次方程解实际问题的运用，销售问题的数量关系利润=售价﹣进价的运用，解答时根据销售问题的数量关系建立方程是关键．　15．（3分）(2014年宁夏)如图，在四边形ABCD中，AD∥BC，AB=CD=2，BC= 5，∠BAD的平分线交BC于点E，且AE∥CD，则四边形ABCD的面积为　　．【考点】平行四边形的判定与性质；等边三角形的判定与性质．【分析】根据题意可以判定△ABE是等边三角形，求得该三角形的高即为等腰梯形ABCD的高．所以利用梯形的面积公式进行解答．【解答】解：如图，过点A作AF⊥BC于点F． ∵AD∥BC， ∴∠DAE=∠AEB，又∵∠BAE=∠DAE， ∴∠BAE=∠AEB， ∵AE∥CD， ∴∠AEB=∠C， ∵AD∥BC，AB=CD=2， ∴四边形是等腰梯形， ∴∠B=∠C， ∴△ABE是等边三角形， ∴AB=AE=BE=2，∠B=60°， ∴AF=AB•sin60°=2× ∵AD∥BC，AE∥CD， =，∴四边形AECD是平行四边形， ∴AD=EC=BC﹣BE=5﹣2=3， ∴梯形的面积= （AD+BC）×AF= ×（3+5）× =4 ．【点评】本题考查了等边三角形的判定和性质，平行四边形的判定和性质，等腰梯形的性质等．　16．（3分）(2014年宁夏)如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面的半径是　．【考点】三角形的外接圆与外心．【专题】网格型．【分析】根据题意得出△ABC的外接圆的圆心位置，进而利用勾股定理得出能够完全覆盖这个三角形的最小圆面的半径．【解答】解：如图所示：点O为△ABC外接圆圆心，则AO为外接圆半径，故能够完全覆盖这个三角形的最小圆面的半径是：故答案为：．．【点评】此题主要考查了三角形的外接圆与外心，得出外接圆圆心位置是解题关键．　三、解答题（共24分） 17．（6分）(2014年宁夏)计算：（﹣ ）﹣2+ ﹣2sin45°﹣|1﹣ |．【考点】实数的运算；负整数指数幂；特殊角的三角函数值．【分析】本题涉及负整指数幂、特殊角的三角函数值、二次根式化简三个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果【解答】解：原式= +﹣﹣（ ﹣1） =．【点评】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算．　18．（6分）(2014年宁夏)化简求值：（ b=1+ ﹣）÷ ，其中a=1﹣ ，．【考点】分式的化简求值．【专题】计算题．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，将a与b的值代入计算即可求出值．【解答】解：原式= •==•，当a=1﹣ ，b=1+ 时，原式= ．【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．　19．（6分）(2014年宁夏)在平面直角坐标系中，△ABC的三个顶点坐标分别为 A（﹣2，1），B（﹣4，5），C（﹣5，2）．（1）画出△ABC关于y轴对称的△A1B1C1；（2）画出△ABC关于原点O成中心对称的△A2B2C2．【考点】作图-旋转变换；作图-轴对称变换．【专题】作图题．【分析】（1）根据网格结构找出点A、B、C关于y轴对称的点A1、B1、C1的位置，然后顺次连接即可；（2）根据网格结构找出点A、B、C关于原点对称的点A2、B2、C2的位置，然后顺次连接即可．【解答】解：（1）△A1B1C1如图所示；（2）△A2B2C2如图所示．【点评】本题考查了利用旋转变换作图，利用轴对称变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键．　20．（6分）(2014年宁夏)在△ABC中，AD是BC边上的高，∠C=45°，sinB= ， AD=1．求BC的长．【考点】解直角三角形；勾股定理．【分析】先由三角形的高的定义得出∠ADB=∠ADC=90°，再解Rt△ADB，得出A B=3，根据勾股定理求出BD=2 ，解Rt△ADC，得出DC=1；然后根据BC=BD+ DC即可求解【解答】解：在Rt△ABD中，∵ ，又∵AD=1， ∴AB=3， ∵BD2=AB2﹣AD2， ∴．在Rt△ADC中，∵∠C=45°， ∴CD=AD=1． ∴BC=BD+DC= +1．【点评】本题考查了三角形的高的定义，勾股定理，解直角三角形，难度中等，分别解Rt△ADB与Rt△ADC，得出BD=2 ，DC=1是解题的关键．　四、解答题（共48分） 21．（6分）(2014年宁夏)如图是银川市6月1日至15日的空气质量指数趋势折线统计图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气质量重度污染．某人随机选择6月1日至6月14日中的某一天到达银川，共停留2天．（1）求此人到达当天空气质量优良的天数；（2）求此人在银川停留2天期间只有一天空气质量是重度污染的概率；（3）由折线统计图判断从哪天开始连续三天的空气质量指数方差最大（只写结论）．【考点】折线统计图；方差；概率公式．【分析】（1）根据折线图找出空气质量指数小于100的天数即可；（2）首先表示出连续两天的空气质量指数情况，再找出2天期间只有一天空气质量是重度污染的数量，再利用概率公式进行计算即可；（3）根据折线图可得5、6、7三天数据波动最大，因此方差最大．【解答】解：（1）此人到达当天空气质量优良的有：第1天、第2天、第3天、第7天、第12天，共5天；（2）．此人在银川停留两天的空气质量指数是：（86，25），（25，57），（ 57，143），（143，220），（220，158），（158，40），（40，217），（217，160），（160，128），（128，167），（167，75），（75，106），（106，180），（180，175），共14个停留时间段，期间只有一天空气质量重度污染的有：第4天到、第5天到、第7天到及第8天到．因此，P（在银川停留期间只有一天空气质量重度污染）= ；（3）根据折线图可得从第5天开始的第5天、第6天、第7天连续三天的空气质量指数方差最大．【点评】此题主要考查了看折线图，以及概率，关键是正确从折线图中获取所需要的信息．　22．（6分）(2014年宁夏)在平行四边形ABCD中，将△ABC沿AC对折，使点B 落在B′处，A B′和CD相交于点O．求证：OA=OC．【考点】平行四边形的性质；翻折变换（折叠问题）．【专题】证明题．【分析】由在平行四边形ABCD中，将△ABC沿AC对折，使点B落在B′处，即可求得∠DCA=∠B′AC，则可证得OA=OC．【解答】证明：∵△AB′C是由△ABC沿AC对折得到的图形， ∴∠BAC=∠B′AC， ∵在平行四边形ABCD中，AB∥CD， ∴∠BAC=∠DCA， ∴∠DCA=∠B′AC， ∴OA=OC．【点评】此题考查了平行四边形的性质、等腰三角形的判定与性质以及折叠的性质．此题难度不大，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想的应用．　23．（8分）(2014年宁夏)在等边△ABC中，以BC为直径的⊙O与AB交于点D， DE⊥AC，垂足为点E．（1）求证：DE为⊙O的切线；（2）计算．【考点】切线的判定；等边三角形的性质．【分析】（1）连接OD，根据等边三角形性质得出∠B=∠A=60°，求出等边三角形BDO，求出∠BDO∠A，推出OD∥AC，推出OD⊥DE，根据切线的判定推出即可；（2）求出AD= AC，求出AE= AC，CE= AC，即可求出答案．【解答】（1）证明：连接OD， ∵△ABC为等边三角形， ∴∠ABC=60°，又∵OD=OB， ∴△OBD为等边三角形， ∴∠BOD=60°=∠ACB， ∴OD∥AC，又∵DE⊥AC， ∴∠ODE=∠AED=90°， ∴DE为⊙O的切线；（2）解：连接CD， ∵BC为⊙O的直径， ∴∠BDC=90°，又∵△ABC为等边三角形， ∴AD=BD= AB，在Rt△AED中，∠A=60°， ∴∠ADE=30°， ∴AE= AD= AC，CE=AC﹣AE= AC， ∴=3．【点评】本题考查了等边三角形的性质和判定，平行线的判定，切线的判定的应用，主要考查学生运用定理进行推理的能力．　24．（8分）(2014年宁夏)在平面直角坐标系中，已知反比例函数y= 的图象经过点A（1，）．（1）试确定此反比例函数的解析式；（2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB，判断点B 是否在此反比例函数的图象上，并说明理由．【考点】反比例函数图象上点的坐标特征；待定系数法求反比例函数解析式；勾股定理；坐标与图形变化-旋转．【分析】（1）根据反比例函数图象上点的坐标特征计算k的值；（2）过点A作x轴的垂线交x轴于点C，过点B作x轴的垂线交x轴于点D，在Rt△ AOC中，根据勾股定理计算出OA=2，利用含30度的直角三角形三边的关系得到∠OAC=30°，则∠AOC=60°，再根据旋转的性质得∠AOB=30°，OB=OA=2，所以 ∠BOD=30°，在Rt△BOD中，计算出BD= OB=1，OD= BD= ，于是得到B 点坐标为（，1），然后根据反比例函数图象上点的坐标特征判断B点在反比例函数图象上．【解答】解：（1）把A（1，）代入y= ，得k=1× =，∴反比例函数的解析式为y= ；（2）点B在此反比例函数的图象上．理由如下：过点A作x轴的垂线交x轴于点C，过点B作x轴的垂线交x轴于点D，如图，在Rt△AOC中，OC=1，AC= ，OA= =2， ∴∠OAC=30°， ∴∠AOC=60°， ∵线段OA绕O点顺时针旋转30°得到线段OB， ∴∠AOB=30°，OB=OA=2， ∴∠BOD=30°，在Rt△BOD中，BD= OB=1，OD= BD= ，∴B点坐标为（，1）， ∵当x= 时，y= =1， ∴点B（，1）在反比例函数的图象上．【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数y= （k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即x y=k．也考查了旋转的性质和勾股定理．　25．（10分）(2014年宁夏)某花店计划下个月每天购进80只玫瑰花进行销售，若下个月按30天计算，每售出1只玫瑰花获利润5元，未售出的玫瑰花每只亏损3 元．以x（0＜x≤80）表示下个月内每天售出的只数，y（单位：元）表示下个月每天销售玫瑰花的利润．根据历史资料，得到同期下个月内市场销售量的频率分布直方图（每个组距包含左边的数，但不包含右边的数）如图所示：（1）求y关于x的函数关系式；（2）根据频率分布直方图，计算下个月内销售利润少于320元的天数；（3）根据历史资料，在70≤x＜80这个组内的销售情况如下表： 70 172 274 375 477 379 2销售量/只天数计算该组内平均每天销售玫瑰花的只数．【考点】频数（率）分布直方图；函数关系式；加权平均数．【专题】图表型．【分析】（1）根据利润等于售出的玫瑰花的利润与未售出的玫瑰花亏损的钱数之和列式整理即可得解；（2）列不等式求出利润小于320元时卖出的玫瑰花的只数，然后根据频率求解即可；（3）利用加权平均数的计算方法列式计算即可得解．【解答】解：（1）y=5x﹣（80﹣x）×3=8x﹣240（0＜x≤80）；（2）根据题意，得 8x﹣240＜320，解得，x＜70，表明玫瑰花的售出量小于70只时的利润小于320元，则50≤x＜60的天数为：0.1×30=3（天）， 60≤x＜70的天数为：0.2×30=6（天）， ∴利润少于320元的天数为 3+6=9（天）；（3）该组内平均每天销售玫瑰：75+ =75（只）．【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．　26．（10分）(2014年宁夏)在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．（1）试说明不论点P在BC边上何处时，都有△PBQ与△ABC相似；（2）若AC=3，BC=4，当BP为何值时，△AQP面积最大，并求出最大值；（3）在Rt△ABC中，两条直角边BC、AC满足关系式BC=λAC，是否存在一个λ 的值，使Rt△AQP既与Rt△ACP全等，也与Rt△BQP全等．【考点】相似形综合题．【分析】（1）利用“两角法”可以证得△PBQ与△ABC相似；（2）设BP=x（0＜x＜4）．由勾股定理、（1）中相似三角形的对应边成比例以及三角形的面积公式列出S与x的函数关系式，利用配方法求得二次函数的最值；（3）利用全等三角形的对应边相等得到AQ=AC，AQ=QB，即AQ=QB=AC．在Rt△ABC中，由勾股定理得 BC2=AB2﹣AC2，易求得：BC= AC，则λ= 【解答】解：（1）不论点P在BC边上何处时，都有．∠PQB=∠C=90°，∠B=∠B ∴△PBQ∽△ABC；（2）设BP=x（0＜x＜4），由勾股定理，得 AB=5 ∵由（1）知，△PBQ∽△ABC， ∴，即 ∴S△APQ ===∴当时，△APQ的面积最大，最大值是；（3）存在． ∵Rt△AQP≌Rt△ACP ∴AQ=AC 又Rt△AQP≌Rt△BQP ∴AQ=QB ∴AQ=QB=AC 在Rt△ABC中，由勾股定理得 BC2=AB2﹣AC2 ∴BC= AC ∴λ= 时，Rt△AQP既与Rt△ACP全等，也与Rt△BQP全等．【点评】本题综合考查了相似三角形的判定与性质，全等三角形的性质，三角形的面积公式以及二次函数的最值的求法等知识点．难度较大．注意，在证明三角形相似时，充分利用公共角，在利用全等三角形的性质时，要找准对应边．